Асанов А.З. Введение в математическое моделирование динамических систем
Подождите немного. Документ загружается.

Ко ениям личество скалярных входов и выходов удовлетворяет соотнош
12
s
m=
Уравнения аимосвязи подсистем можно записать следующим образом:
(
знак «-» в формуле соответствует отрицательной обратной связи)
етствующем встречно-
пара
) (),
() () ()() (),
() () () 0.
и
12
ms=
.
вз
12 12
() () (), () () ()up up yp yp yp up=± = =
. (6.2.7)
Представим уравнения (6.1.14) в виде, соотв
ллельному соединению двух подсистем:
()() () (
0
1111
0
22 2 2
12
A
pyp B pu p y p
A
py p B pyp y p
up up yp
=
−=
−± =
Дополним последние уравнения регуляризирующим тождеством и
запи г
л с
1
0
22
2
2
1
()
()
() () 0 0
()
()
0
()
0
()
()
000
mm m
s
yp
yp
Bp Ap
yp
yp
II I
up
up
up
I
⎤
⎡⎤
⎡⎤
⎢⎥
⎢⎥
⎢⎥
−
⎢⎥
⎢⎥
⎢⎥
=
⎢⎥
−
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎣⎦
⎣⎦
⎣⎦
∓
.
Отсюда проматрица встречно-параллельного соединения двух систем,
зада
2
22
() () 0 0
()
0
000
mm m
s
Bp Ap
p
−
шем полученную систему уравнений в виде блочно-матрично о
обобщенного уравнения инейной истемы:
11
() 0 () 0Ap Bp
−
⎡
22 2
0
нных уравнениями в форме левой факторизации, имеет вид
11
() 0 () 0Ap Bp
22
I
II
I
∗
⎢⎥
−
⎢⎥
′
Ω=
⎢⎥
−
⎢⎥
⎢⎥
⎣⎦
∓
. (6.2.8)
(
знак «+» перед единичной матрицей размера т
2
третьей блочной строки и второго блочного
й системы можно учесть второе
урав
ь
построений мож
2
0()0 ()0
00
()
00 0
00 0 0
mm m
mm
s
Ap Bp
II I
p
II
I
∗
⎢⎥
−
⎢⎥
⎢⎥
−
Ω=
⎢⎥
−
⎢⎥
⎢⎥
⎣⎦
∓
. (6.2.9)
−
⎡⎤
столбца соответствует отрицательной обратной связи
)
При формировании проматрицы данно
нение взаимосвязи (6.2.7) не как изменение переменной
2
()up
, а как
уравнение статического объекта с единичным оператор виде
2
() () 0up yp−=
, и дописат его к уравнениям системы. После аналогичных
но получить, что проматрица системы примет вид
() 0 () 0 0Ap Bp−
⎡⎤
ом в
22
11
11
22
187
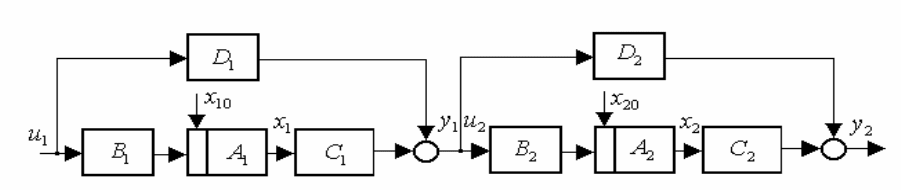
При использовании описаний систем в пространстве состояний,
применяя аналогичный подход, можно получить проматрицы системы при
типовых соединениях подсистем в несколько другом виде.
Так, при последовательном соединении подсистем (рис. 6.2.4)
Рис. 6.2.4. Последовательное соединение подсистем
обобщенное уравнение линейной системы имеет вид
(
)
()
1
1
2
2
22
0 0
m
2
2
000
0000
m
11
11
1
10
11
1
20
2
2
2
0000
000
0
00
0
0
n
m
mm
pI A B
x
1
1
00 000
s
x
CID
y
x
I
u
u
x
pI A B
y
−−
⎢⎥
⎢⎥
CID
II
⎢
⎢
−
u
⎡⎤
−−
⎡⎤
⎡⎤
⎢⎥
⎢⎥
⎢⎥
⎢⎥
−−
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
=
⎢⎥
⎢⎥
⎢⎥
⎢⎥
−−
⎢⎥
⎢⎥
⎥
⎣⎦
⎣⎦
⎥
⎣⎦
.
Проматрица системы, состоящей из последовательного соединения двух
подсистем, в задаче моделирования, таким образом, имеет вид
⎢⎥
⎢⎥
⎢⎥
(
)
()
1
1
2
2
22
2
000
0000
n
m
CID
11
11
11
2
0000
000
00 000
()
000 0
n
m
s
mm
pI A B
CID
I
p
pI A B
I
I
⎡⎤
−−
⎢⎥
⎢⎥
−−
⎢⎥
⎢⎥
Ω=
⎢⎥
−−
⎥
⎥
⎣⎦
.
При учете того, что
, размеры обобщенного уравнения и
проматрицы могут быть уменьшены на единицу. В этом случае обобщенное
уравнение принимает вид
⎢⎥
⎢⎥
−−
⎢
⎢
−
21
uy=
(
)
()
1
1
2
2
11
11
11
1
22
22
2
22
11
000
00
0
000
0
00
00 00
n
m
n
m
s
pI A B
0
0
x
x
CI D
y
x
x
BpIA
y
DCI
uu
I
⎡⎤
−−
⎡
⎤⎡ ⎤
⎢⎥
⎢
⎥⎢ ⎥
⎢⎥
−−
⎢
⎥⎢ ⎥
⎢⎥
⎢
⎥⎢ ⎥
=
⎢−− ⎥
⎢
⎥⎢ ⎥
⎢⎥
⎢
⎥⎢ ⎥
−−
⎢⎥
⎢
⎥⎢ ⎥
⎢⎥
⎣
⎦⎣ ⎦
⎣⎦
,
188
а пр
1
2
2
11
22
22
00
()
000
00
0000
m
n
m
s
CI D
p
BpIA
DCI
оматрица
()
1
11
000
n
pI A B
⎡⎤
−−
()
I
⎢⎥
⎥
−−
⎢⎥
′
Ω=
⎢−− ⎥
⎢⎥
−−
⎢⎥
⎢⎥
⎣⎦
.
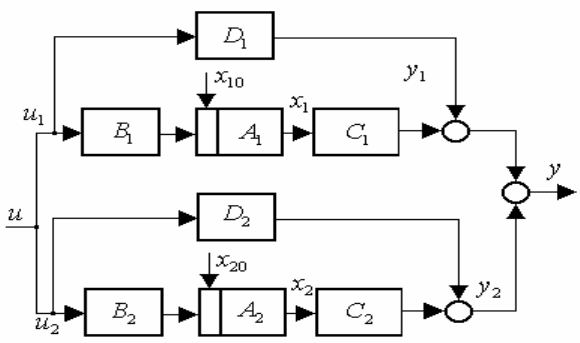
При параллельном соединении подсистем (рис. 6.2.5) обобщенное
уравнение и выглядят
следующим
⎢
Рис. 6.2.5. Параллельное соединение подсистем
проматрица системы в задаче моделирования
образом
(
)
()
1
1
2
2
12
mmm
11
110
11
1
220
12
2
22
0000
000
0
00 00
0
00 0
0
00 0
0 0
n
m
n
m
pI A B
00 0
s
x
x
CI D
y
x
x
pI A B
y
CI D
y
III
u
⎡⎤
−−
⎡⎤⎡ ⎤
⎢⎥
⎢⎥⎢ ⎥
⎢⎥
−−
⎢⎥⎢ ⎥
⎢⎥
⎢⎥⎢ ⎥
−−
⎢⎥
=
⎢⎥⎢ ⎥
⎢⎥
⎢⎥⎢ ⎥
−−
⎢⎥
⎢⎥⎢ ⎥
⎢⎥
−−
u
I
⎣⎦
(
⎢⎥⎢ ⎥
⎢⎥
⎣ ⎦
⎢⎥
,
⎣⎦
)
()
1
1
2
2
12
11
11
12
22
0000
000
00 00
()
00 0
00
00000
n
m
n
m
mmm
s
p
0
IA B
CI D
p
IA B
p
CI D
III
I
⎡⎤
−−
⎢⎥
⎢⎥
−−
⎢⎥
−−⎢⎥
Ω=
⎢⎥
−−
⎢⎥
⎢⎥
−−
⎢⎥
⎢⎥
⎣⎦
,
189
или с уменьшенным числом компонент обобщенного вектора за счет
совмещения некоторых из них, а значит, с уменьшенным размером
проматрицы
(
)
()
1
2
11
11
22
12
1212
00
00
0
000
n
n
m
s
pI A B
0
0
x
x
x
x
pI A B
y
CCIDD
uu
I
⎡⎤
−−
⎡
⎤⎡ ⎤
⎢⎥
⎢
⎥⎢ ⎥
⎢⎥
−−
⎢
⎥⎢ ⎥
=
⎢⎥
⎢
⎥⎢ ⎥
⎢⎥
−− +
⎢
⎥⎢ ⎥
⎢⎥
⎣
⎦⎣ ⎦
⎣⎦
,
(
)
()
1
2
11
12
121
00
00
()
000
n
n
m
s
pI A B
pI A B
p
CCID
I
⎡⎤
−−
⎢⎥
⎢⎥
−−
′
Ω=
⎢⎥
⎢⎥
−− +
⎢⎥
⎣⎦
.
2
D
(Предполагается, что размеры матриц согласованы, так как только в этом случае возможно
говорить о соединении матричных систем (MIMO – систем)).
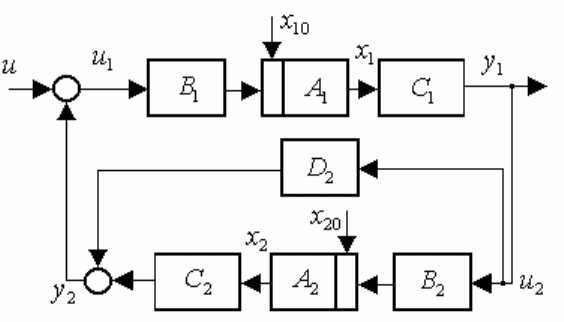
П и л
Рис. 6.2.6. Встречно-параллельное соединение подсистем
обобщенное уравнение и проматрица системы в задаче
имеют вид
1
2
2
12
11
1
220
22
2
22
2
00000
000 0 0
0
000 0
0
00000
000 0 00
n
n
m
s
s
pI A B
р встречно-пара лельном соединении двух подсистем (рис. 6.2.6)
моделирования
()
1
110
1
00 000
0
m
x
x
()
12
00 0 0
0
sms
CI
y
III
x
x
pI A B
y
CID
u
II
uu
I
⎡⎤
−−
⎡
⎤⎡ ⎤
⎢⎥
⎢
⎥⎢ ⎥
⎢⎥
−
ε
⎢
⎥⎢ ⎥
⎥⎢
⎢
⎥⎢ ⎥
⎢⎥
⎢
⎥⎢ ⎥
⎢⎥
∓
=
−−
⎢
⎥⎢ ⎥
⎢⎥
⎢
⎥⎢ ⎥
⎢⎥
−−
⎢
⎥⎢ ⎥
⎢⎥
⎢
⎥⎢ ⎥
⎢⎥
−
⎢
⎥⎢ ⎥
⎢⎥
⎣
⎦⎣ ⎦
⎢⎥
⎣⎦
,
190
(
)
1
11n
()
1
12
2
2
12
1
22
22
0
00 000
00 0 0
()
000 0 0
000 0
00000
000 0 00
m
0000pI A B
⎡
⎤
−−
s
ms
n
m
s
s
CI
I
II
p
pI A B
CID
II
I
⎢
⎥
⎢
⎥
−
⎢
⎥
⎢
⎥
⎢
⎥
Ω=
−−
⎢
⎥
⎢
⎥
−−
⎢
⎥
⎢
⎥
−
⎢
⎥
⎢
⎥
⎣
⎦
∓
.
(Предполагается, что размеры матриц согласованы, так как только в этом случае корректно
говорить о соединении матричных систем (MIMO – систем). В компоненте
знак «минус»
соответствует положительной обратной связи, знак «плюс» – соответственно, отрицательной
обратной связи в системе.)
При другом выборе компонент обобщенного вектора системы (при
объединении записи некоторых уравнений) можно получить обобщенное
уравнение системы и проматрицу в следующем виде
2
m
I∓
(
)
()
1
1
2
2
111
11
1
1
22
22
2
22
00
000
0
000
0
00
0000
n
m
n
m
0
0
pI A B B
s
x
x
CI
y
x
x
BpIA
y
DCI
uu
I
⎡⎤
−
⎡
⎤⎡ ⎤
⎢⎥
⎢
⎥⎢ ⎥
⎢⎥
−
⎢
⎥⎢ ⎥
⎢⎥
⎢
⎥⎢ ⎥
=
⎢−− ⎥
⎢
⎥⎢ ⎥
⎢⎥
⎢
⎥⎢ ⎥
−−
⎢⎥
⎢
⎥⎢ ⎥
⎢⎥
⎣
⎦⎣ ⎦
∓
,
0
⎣⎦
()
1
111
1
00
000
n
m
()
2
2
22
22
()
000
00
000
n
m
1
p
IA BB
CI
⎡⎤
−
⎢⎥
⎢⎥
−
∓
s
p
BpIA
DCI
⎢⎥
′
Ω=
⎢−− ⎥
I
⎢⎥
⎦
.
Таким образом, в зависимости от способа записи уравнений связи (или
других дополнительных соотношений) проматрицы одной и той же со-
ставной системы даже в одной и той же задаче могут принимать различные
размеры (проматрицы
и
−−
⎢⎥
⎢⎥
⎣
...
()pΩ
...
()p
′
Ω
в каждом рассмотренном случае). При
этом общие свойства проматриц остаются в силе. Однако различие структур
проматриц может быть сопряжено с различием в полноте описания и
представления различных сторон системы.
191
6.3. Возмущения линейных систем и проматрицы
Невозможно представить функционирование систем без учета
различного рода возмущений. Поэтому, вводя новые математические
конструкции, логично рассмотреть модели действия возмущений в терминах
этих новых конструкций, в частности, проматриц.
Рассмотрим непараметрические (сигнальные) и параметрические
возм
но и рпрет
ущения.
Структура обобщенного уравнения линейной системы (6.1.7) и
обобщенного входа (6.1.6) позволяет введение дополнительных входных
сигналов, которые мож нте ировать как различные
возмущающие
воздействия на систему.
Рассмотрим уравнения
(
)
() ()pI A x p Bu p−=+
0
()
() () () ()
n
Rw p x
yp Cxp Dup p
δ
++∆
=+ +
(6.3.1)
или
L 0
()() ()() ()() ()
L
A
pyp B up Spwp y p=+++∆
(6.3.2)
Здесь
R и
()Sp
– числовая и полиномиальная матрицы соответственно
размеров
dim ( )nwp×
и
dim ( )mwp×
, характеризующие воздействие на
систему возмущения
()wp
, аналогичного по
p
природе управляющему
возд
е
ействию
()up
; ∆ – непреднамеренное изменени начальных условий
системы, возникающее по разным причинам;
()p
δ
–
m
-мерный вектор
возмущений, действие которых можно свести к выходу статического звена
(алгебраического уравнения) модели системы.
Аналогично ранее рассмотренному, можно ввести расширенные
обоб асширенную проматрицу
,
щенные выход, вход и р
()
()
()
()
()
x
yp
Yp
up
wp
⎡⎤
⎢⎥
⎢⎥
=
⎢⎥
⎢⎥
⎣⎦
0
()
()
()
()
x
p
Up
up
wp
δ
+∆
⎡⎤
⎢⎥
⎢⎥
=
⎢⎥
⎢⎥
⎣⎦
,
()
00 0
000
n
m
s
0
0
p
IA B R
CI
p
I
D
−
−−
⎡
⎤
⎢
⎥
−−
⎢
⎥
I
Ω=
⎢
⎥
⎢
g
⎥
⎣
⎦
. (6.3.3)
пр ениеО едел 3.7.
Матрица-столбец, составленная из субвекторов,
0
*
()
()
()
()
x
p
Up
up
wp
δ
+
∆
⎡
⎤
⎢
⎥
⎢
⎥
=
⎢
⎥
⎢
⎥
⎣
⎦
192
называется обобщенным входом системы непараметрическими
возмущениями
.
Таким образом, обобщенное уравнение ли
с
нейной системы при внешних
(неп и тараметрическ х) возмущениях принимае вид
*
()() ()
p
Yp U pΩ=
, (6.3.4)
где в правой части стоит обобщенный вход системы с возмущениями,
действующими на нее и приводимыми к различным входным и внутренним
сигналам систем
Заметим, что уравнение (6.3.4) описывает влияние на линейную систему
всех непараметрических возмущений. При этом наличие или отсутствие этих
возм
ими
словами, в проматрице независимо от исследователя присутствуют
конструкции, определяющие влияние тех или иных непараметрических
возмущений на поведение рассматриваемой линейной системы.
в и
овых или полиномиальных матриц коэффициентов,
фигу
ства состояний новые,
возмущенные,
матрицы числовых коэффициен
ы.
ущений никак не влияет на структуру проматрицы
()pΩ
. Друг
К параметрическим озмущен ям принято относить какие-либо
изменения числ
рирующих в формулах. Рассмотрим только аддитивными возмущениями
этих матриц, когда, например, для простран
тов принимают значения
A
A+∆ , BB
+
∆ , CC
+
∆ , DD
+
∆ ,
а в левой факторизации недробные полиномиальные матрицы уступают
место матрицам такого же типа
() ()
L
A
pAp
+
∆
,
() ()
L
Bp Bp
+
∆
.
В результате при формировании проматрицы какой-либо системы
получается проматрица с параметрическими возмущениями
() ()pp
Ω
−∆Ω
,
где
()p∆Ω
– аддитивная добавка к невозмущенной проматрице этой же
системы.
В частности, для проматрицы (6.1.8)
,
,,
0
()
00
nnm
m
sn sm s
p
IA B
p
CI D
I
⎡
⎤
−
−
⎢
⎥
Ω
=− −
⎢
⎥
⎢
⎥
⎣
⎦
193
такая добавка имеет вид
0
()
A
B
∆
∆
⎡
⎤
0
p
CD
⎢
⎥
= ∆ ∆∆Ω
000
⎢
⎥
⎢
⎥
⎣
⎦
.
ее.
Определение 6.8.
Блочно-матричное уравнение
Особенностью представленных параметрических возмущений является
неразрушение общих свойств проматриц, перечисленных ран
[]
() () () ()
p
pYp UpΩ−∆Ω =
, (6.3.5)
связывающее обобщенные вход U(p) и выход Y(p) системы, называется
обоб параметрически возмущенной
системы
.
Таким образом, исследование влияния непараметрических возмущений
на поведение линейной системы связано с использованием обобщенного
уравнения линейной системы (6.3.4), а исследование влияния
параметрических возмущений – с использованием обобщенного уравнения
, имеет вид
которое представляет собой отображение или преоб
процедурами и результатами составления дифференциальных
урав
е
,
которое представляет собой фактически разрешение обобщенного уравнения
лине
щенным уравнением линейной
линейной системы (6.3.5).
3.4. Реверсивная проблемная матрица системы
Обобщенное уравнение линейной системы, как было установлено
()() ()pY p U pΩ=
,
разование обобщенного
выхода
()Yp
в обобщенный вход
()Up
. Такой характер отображения
обусловлен
нений динамических систем.
Однако исследователей чаще интересует обратное отображение,
преобразующее входно воздействие
()Up
в соответствующую ему
выходную реакцию
()Yp
системы
1
() () ()Yp pUp
−
=Ω
йной системы относительно
()Yp
.
Определение 6.9. Квадратная дробно-полиномиальная матрица
1
()
p
−
Ω
,
которая обобщенному входу
ставит в ответствие
ной
кратко, реп
системы в конкретной задаче.
()Up
со обобщенный
выход
()Yp
no формуле
1
() () ()Yp pUp
−
=Ω
, называется реверсивной
проблем матрицей
, или, роматрицей рассматриваемой
194
По аналогии с широко применяемыми в инженерной практике
передаточными матрицами (матричными передаточными функциями)
репроматрицу
1
()
p
−
Ω
можно рассмат ивать как обобщенную ередаточную
матрицу от об бщенного входа
(Up
б бщенному выходу
()Yp
.
Обобщенной она является потому
р п
к о о
, что содержит все возможные переда-
точные матрицы от всех субвекторов, включенн в обобщенный вход, ко
репроматриц – взаимнооднозначное
соот
о
)
ых
всем субвекторам, включенным в обобщенный выход.
Отметим принципиальное свойство
ветствие проматрицы и репроматрицы
1
() ()
p
p
−
Ω→Ω
и
1
() ()
p
p
−
Ω→Ω
.
Эт йство очевидно тности и невырожденности
проматриц юбых систем характеризует то обстоятельство, что
совокупность всех переда
о сво из свойств квадра
л и
точных функций линейной системы,
стру и
тся и ч в
лу суперпозиции и в
соот
p
(6.4.1)
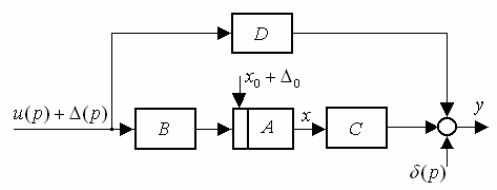
Рассмотрим линейную динами стему (рис.3.4.1), модель которой
пред
е б щ
су ра го ы
Рис. 6.4.1 Обобщенная структура линейной динамической системы
ктур рованная определенным образом (речь идет о структуре ре-
проматрицы), полностью эквивалентна исходным уравнениям линейной
системы.
Принципиально важным являе то, то введенная рассмотрение
репроматрица допускает обобщение на
случай действия непараметрических
возмущений
*
() () ()U p Up Up=+∆
. В этом случае непараметрически
возмущенное движение
()Yp
линейной системы в си
ветствии с уравнением (3.3.4) будет определяться формулой
1*
() ()Yp pU
−
=Ω ()
ческую си
ставлена соответствующими уравнениями в пространстве состояний.
Блочно (поэлементное) о ра ение проматрицы системы в соответствии
с введенными бвекто ми обобщенно входа и обобщенного в хода дает
аналитические выражения матричных (скалярных) передаточных функций
этой системы.
195

Наименование каждой такой скалярной передаточной функции и
передаточной матрицы можно установит
ком
ь по последовательностям
понент и субвекторов в обобщенном входе и обобщенном выходе
системы.
Так, если уравнение вида
)()()(
1
pUppY
∗
−
Ω= расписать по блокам, то
репроматрица будет содержать передаточные функции:
0
1
() () () ()
() (
x
u
xxx
xp x FpFpFp x
yp p
δ
−
⎡⎤
+∆ +∆
⎡⎤ ⎡ ⎤ ⎡ ⎤
⎢⎥
=Ω
0
00 00
) () () () () ()
() () () 0 0 () ()
x
u
yyy
S
p F p F p F p p
up up p I up p
δ
δδ
⎢⎥
⎢ ⎥ ⎢ ⎥
=
⎢⎥
⎢⎥ ⎢ ⎥ ⎢ ⎥
⎢⎥
⎢⎥ ⎢ ⎥ ⎢ ⎥
+∆ +∆
⎣⎦ ⎣ ⎦ ⎣ ⎦
⎣⎦
.(6.4.2)
Здесь использованы обозначения передаточных матриц
()
вх
вых
F
p
(сигналы
от
некоторого входного сигнала к некоторому выходному сигналу в
общем случае могут быть векторными). В последней блочной строке
репроматр , что по
опре
д
к си м
е
дет недробной. В этом случае определены дополнительные общие
свойс с ее обращением:
ическому полиному
системы, т.е.
ицы расставлены нулевые и единичный блоки из-за того
делению входной вектор
()up
не зависит от ругих переменных.
Можно показать, что огда модели всех под сте заданы уравнениями
в пространств состояния или в факторизованной форме, то проматрица
системы бу
тва проматрицы, связанные
− определитель проматрицы соответствует характерист
det ( ) ( )pp
χ
Ω=
;
− присоединенная матрица от соответствует матрице несокращ
числителей всех передаточных функций системы, т.е.
.
извест
()pΩ
енных
() ()
ij
adj p b p
⎡⎤
Ω=
⎣⎦
Способы формального получения репроматрицы, используя ные
методы обращения матриц, могут быть различны.
Один из них основан на вычислении присоединенной матрицы и
делении ее на детерминант исходной матрицы:
1
1
) ()(
p
det ( )
adj pΩ= Ω
.
pΩ
Поэлементное обращение проматрицы по этой формуле позволяет
получить любую из скалярных передаточных функций
−
(6.4.3)
()
()
i
yp
fp
=
,
1,im=
, 1,j= s, (6.4.4)
()
ij
j
up
196
