Дипломная работа - Анализ, разработка и программа реализации алгоритмов поиска и оптимизации маршрутов движения в улично-дорожной сети города
Подождите немного. Документ загружается.

2 АЛГОРИТМЫ НА ГРАФАХ
2.1 Основы теории графов
Графы являются существенным элементом математических моделей в самых раз-
нообразных областях науки и практики. Они помогают наглядно представить взаимоот-
ношения между объектами или событиями в сложных системах. Термин «граф» неодно-
значен. Это легко заметить, сравнивая приводимые в разных книгах определения. Однако
во всех этих определениях есть кое-что общее. В любом случае граф состоит из двух
множеств – множества вершин и множества ребер, причем для каждого ребра указана пара
вершин, которые это ребро соединяет [9].
Графом G мы будем называть пару (V(G), E(G)), где V(G) – непустое конечное
множество элементов, называемых вершинами, а E(G) – конечное множество неупорядо-
ченных пар элементов из V(G), называемых ребрами [10]. Мы будем рассматривать только
конечные графы, то есть такие, у которых оба множества конечны. Вершины и ребра гра-
фа будем называть его элементами. Множество вершин графа G будем обозначать через
VG, множество ребер – EG, число вершин – n(G), число ребер – m(G).
Ориентированным графом (орграфом) называется пара G=(V, E), где V – конечное
множество, E – множество упорядоченных пар различных элементов из V [9]. В дальней-
шем термин «граф» будем употреблять в смысле «обыкновенный граф», а рассматривая
другие типы графов, будем специально это оговаривать.
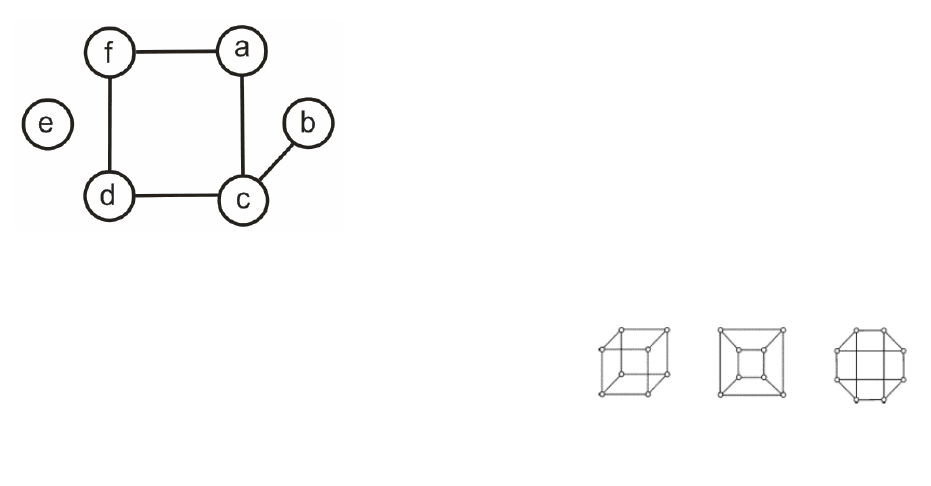
Для задания обыкновенного графа достаточно
перечислить его вершины и ребра, каждое ребро
представлено парой вершин. Положим, например,
VG={a, b, c, d, e, f}, EG={(a,c), (a,f), (b,c), (c,d), (d,f)}.
Тем самым задан граф G с n(G)=6, m(G)=5. Если граф
не слишком велик, то более наглядно представить его
можно с помощью рисунка, на котором вершины
изображаются кружками или иными значками, а
ребра – линиями, соединяющими вершины (рис. 2.1).
Рис. 2.1 – Граф
Рис. 2.2 – Представления куба
в виде графа
Примеры графов легко найти в самых разных областях науки и практики. Сеть до-
рог, трубопроводов, электрическая цепь, структурная
формула химического соединения, блок-схема
программы – в этих случаях графы возникают
естественно и видны «невооруженным глазом».
Немало поводов для появления графов и в
математике. Наиболее очевидный пример – любой
многогранник в трехмерном пространстве. Вершины
и ребра многогранника можно рассматривать как вершины и ребра графа. При этом мы не
обращаем внимание на расположение элементов многогранника в пространстве, оставляя
лишь информацию о том, какие вершины соединены ребрами [9] (рис. 2.2).
Если в графе имеется ребро e=(a,b), то говорят, что вершины a и b смежны в этом
графе, ребро e инцидентно каждой из вершин a, b, а каждая из них инцидентна этому реб-
ру. Множество всех вершин графа, смежных с данной вершиной a, называется окрестно-
стью этой вершины и обозначается через V(a). Число вершин, смежных с вершиной a, на-
зывается степенью вершины a и обозначается через deg(a). Вершину степени 0 называют
изолированной. Граф называют регулярным степени d, если степень каждой его вершины
равна d.
11
2.2 Маршруты, пути, циклы, расстояния
Маршрут в графе – это последовательность вершин x
1
, x
2
… x
n
, такая, что для каж-
дого i=1, 2… n−1 вершины x
i
и x
i+1
соединены ребром. Эти n−1 ребер называются ребрами
маршрута. Говорят, что маршрут проходит через них, а число n−1 называют длиной мар-
шрута. Говорят, что, если маршрут соединяет вершины x
i
и x
n
, то они называются соот-
ветственно началом и концом маршрута, вершины x
2
…x
n
называются промежуточными.
Маршрут называется замкнутым, если x
1
=x
n
.
Путь – это маршрут, в котором все ребра различны. Путь называется простым, ес-
ли и все вершины в нем различны.
Цикл – это замкнутый путь. Цикл x
1
, x
2
… x
n-1
, x
1
называется простым, если все вер-
шины x
1
, x
2
… x
n-1
попарно различны [9].
Установим некоторые простые свойства маршрутов.
1) В любом маршруте, соединяющем две различные вершины, содержится простой
путь, соединяющий те же вершины. В любом цикле, проходящем через некоторое ребро,
содержится простой цикл, проходящий через это ребро.
2) Если в графе степень каждой вершины не меньше 2, то в нем есть цикл. Доказа-
тельство этих свойств можно найти в [9].
Расстоянием между двумя вершинами графа называется наименьшая длина пути,
соединяющего эти вершины. Расстояние между вершинами a и b обозначается через d(a,b).
Если в графе нет пути, соединяющего a и b, то расстояние между ними считается беско-
нечным. Функция d(a,b) обладает следующими свойствами:
1) d(a,b)≥0, причем d(a,b)=0 тогда и только тогда, когда a=b;
2) d(a,b)=d(b,a);
3) d(a,b)+d(b,c)≥d(a,c) (неравенство треугольника).
Расстояние от данной вершины a до наиболее удаленной от нее вершины называет-
ся эксцентриситетом вершины a и обозначается через ecc(a). Таким образом,
ecc(a)=max d(a,x). Вершину с наименьшим эксцентриситетом называют центральной, а
вершину с наибольшим эксцентриситетом – периферийной. Множество всех центральных
вершин называется центром графа. Сама величина наименьшего эксцентриситета называ-
ется радиусом графа и обозначается rad(G), а величина наибольшего – диаметром и обо-
значается diam(G). Наименьший диаметр имеет полный граф (граф, все вершины которого
попарно смежны) – его диаметр равен 1 [
9].
Для ориентированного графа можно определить два типа маршрутов:
1) неориентированный маршрут – это чередующаяся последовательность x
1
, e
1
, x
2
,
e
2
… e
k-1
, x
k
вершин и ребер графа, такая, что для каждого i=1, 2… k−1 выполняется одно из
двух: e
i
=(x
i
, x
i+1
) или e
i
=(x
i+1
, x
i
);
2) маршрут называется ориентированным (или ормаршрутом), если e
i
=(x
i
, x
i+1
) для
каждого i.
Таким образом, при движении вдоль неориентированного маршрута в орграфе реб-
ра могут проходиться как в направлении ориентации, так и в обратном направлении, а при
движении вдоль ормаршрута (или просто маршрута) – только в направлении ориентации.
Это различие очевидным образом распространяется на пути и циклы, так что в орграфе
можно рассматривать пути и орпути, циклы и орциклы. Определимся, что маршрут со-
единяет вершины x
i
и x
k
, а ормаршрут ведет из x
i
в x
k
.
12
2.3 Представление графов в информационных системах
При создании различных информационных систем, связанных с атласами автомо-
бильных дорог, схемами маршрутов передвижения, техническими схемами устройств, ор-
ганизационными схемами управления, с решением задач сетевого планирования неизбеж-
но приходится иметь дело с графами. Графы позволяют решить множество задач: найти
оптимальный маршрут на карте дорог; рассчитать максимальное время выполнения про-
екта (критический путь); определить, сколько элементов должно выйти из строя, чтобы
отказал весь механизм и т. д.
Граф обычно изображают как множество точек на плоскости (вершин графа), со-
единенных линиями (ребрами графа). Очевидно, что это представление не подходит для
решения задач с помощью компьютера. Выбор соответствующей структуры данных для
представления графов оказывает принципиальное влияние на эффективность алгоритмов
[11]. Проанализируем несколько способов представления графов. Для определенности ус-
ловимся, что рассматривать будем только неориентированные графы (для орграфов
рассуждения будут аналогичными). суждения будут аналогичными).
Еще раз вспомним несколько определений из основ
теории графов. Граф есть некоторое множество вершин и
некоторое множество ребер, соединяющих пары
различных вершин [12]. Две вершины называются
смежными, если есть ребро, соединяющее их. Такое ребро
называется инцидентным данным вершинам.
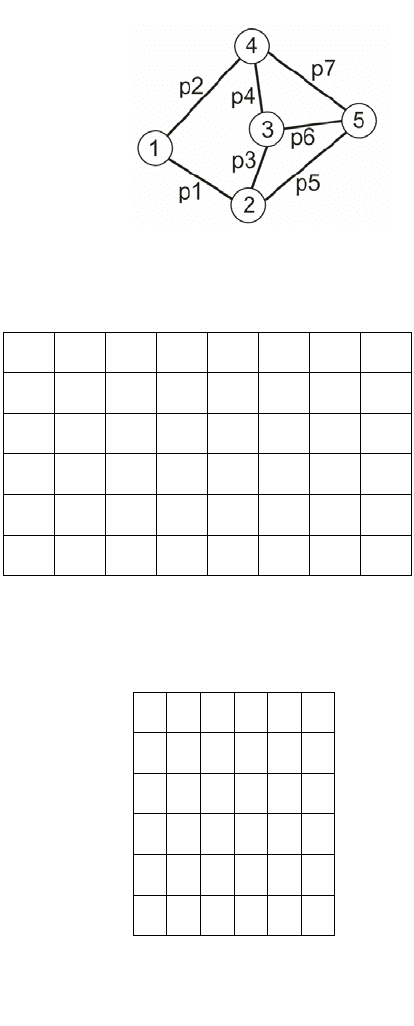
Для примера возьмем конкретный граф. Пусть он
состоит из 5 вершин (пронумеруем их от 1 до 5),
связанных 7 ребрами (обозначим их как «р1» ÷ «р7»)
(рис. 2.3).
Рис. 2.3 – Представление
графа на плоскости
р1 р2 р3 р4 р5 р6 р7
1 1 1
0 0 0 0 0
2 1
0
1
0
1
0 0
3
0 0
1 1
0
1
0
4
0
1
0
1
0 0
1
5
0 0 0 0
1 1 1
Рис. 2.4 – Представление графа в
виде матрицы инциденций
Рассмотрим различные варианты
представления этого графа в информационных
системах. В теории графов классическим
способом представления служит матрица инци-
денций. Это матрица A с n строками,
соответствующими вершинам, и m столбцами,
соответствующими ребрам [11]. Ячейка
матрицы содержит 1, если вершина и ребро
графа, соответствующие строке и столбцу
матрицы инцидентны (рис. 2.4). Матрица
инциденций является одним из самых
неудачных способов представления графа в
информационной системе. Для хранения такой
матрицы (размерность n × m) необходимо достаточно
много памяти, причем большой объем занят нулями.
И ответы на простые вопросы – «Смежны ли
вершины x и y?», «Какие вершины смежны с
вершиной х?» – требуют, в худшем случае, перебора
всех столбцов матрицы.
1 2 3 4 5
1
0
1
0
1
0
2 1
0
1
0
1
3
0
1
0
1 1
4 1
Лучшим способом представления графа явля-
ется матрица смежности, определяемая как матрица
B=[b
ij
] размера n × n, где b
ij
=1, если существует ребро,
идущее из вершины i в вершину j [11] (рис. 2.5). Пре-
имущество матрицы смежности – это то, что за один
0
1
0
1
5
0
1 1 1
0
Рис. 2.5 – Представление графа
в виде матрицы смежности
13

шаг можно ответить на вопрос «Существует ли ребро, связывающее вершины x и y?». Не-
достаток в том, что независимо от числа ребер объем занимаемой памяти пропорционален
n
2
. Если в графе нет петель (вершин, соединенных сами с собой), то на главной диагонали
всегда будут нули. Матрица смежности является симметричной относительно главной
диагонали [12].
1 1 2 2 3 3 4
2 4 3 5 4 5 5
Рис. 2.6 – Представление графа
в виде списка пар,
соответствующих его ребрам
1
2
3
4
5
:
Более экономичным способом представления
графа в памяти (особенно в случае неплотных
графов) является представление его в виде списка
пар, соответствующих ребрам (рис. 2.6). Объем
памяти в этом случае пропорционален 2m.
Недостатком является большое число шагов,
необходимое для определения множества вершин,
смежных с данной, и, как следствие, невысокая
скорость работы различных алгоритмов поиска.
Лучшим решением во многих случаях
оказывается структура данных – список ин-
цидентностей [
11] – или список смежных вершин
[12] (рис. 2.7). Для неориентированного графа
каждое ребро фигурирует в 2 множествах: для
каждого ребра x-y вершина x содержится во
множестве, соответствующем вершине y и наоборот.
Данный способ позволяет быстро решать
поисковые задачи, на которые при использовании
предыдущих требовалось бы гораздо большее
количество шагов. Этот способ представления
является одним из экономичных в отношении
использования памяти.
:
:
:
:
2
1
2
1
2
4
3
4
3
3
5
5
5
4
Рис. 2.7 – Представление графа
в виде списка смежных вершин
У каждого из рассмотренных способов представления графов есть свои недостатки
и свои преимущества. Использование того или иного способа зависит от назначения и за-
дач проектируемой информационной системы.
2.4 Поиск на графах, кратчайшие пути
2.4.1 Поиск в глубину
Работа всякого алгоритма обхода состоит в последовательном посещении вершин и
исследовании ребер. Какие именно действия выполняются при посещении вершины и ис-
следовании ребра – зависит от конкретной задачи, для решения которой производится об-
ход. В любом случае, факт посещения вершины запоминается, так что с момента посеще-
ния и до конца работы алгоритма она считается посещенной. Вершину, которая еще не
посещена, будем называть новой. В результате посещения вершина становится открытой
и остается такой, пока не будут исследованы все инцидентные ей ребра. После этого она
превращается в закрытую [9].
Существует много алгоритмов на графах, в основе которых лежит систематический
перебор вершин, такой, что каждая вершина просматривается в точности один раз. По-
этому важной задачей является нахождение хороших методов поиска в графе. Метод по-
иска хорош, если он позволяет алгоритму решения интересующей нас задачи легко ис-
пользовать этот метод и каждое ребро графа анализируется не более одного раза (или ко-
личество таких исследований ограничено сверху) [11].
14
Поиск в глубину – это наиболее важная ввиду многочисленности приложений стра-
тегия обхода графа. Идея этого метода – идти вперед в неисследованную область, пока это
возможно, если же вокруг все исследовано, отступить на шаг назад и искать новые воз-
можности для продвижения вперед. Метод поиска в глубину известен под разными назва-
ниями: «бэктрекинг», «поиск с возвращением» [9].
Обход начинается с посещения заданной стартовой вершины a, которая становится
активной и единственной открытой вершиной. Затем выбирается инцидентное вершине a
ребро (a, y) и посещается вершина y. Она становится открытой и активной. В дальнейшем,
как и при поиске в ширину, каждый очередной шаг начинается с выбора активной верши-
ны из множества открытых вершин. Если все ребра, инцидентные активной вершине x,
уже исследованы, она превращается в закрытую. В противном случае выбирается одно из
неисследованных ребер (x, y), это ребро исследуется. Если вершина y новая, то она посе-
щается и превращается в открытую.
При поиске в глубину в качестве активной выбирается та из открытых вершин, ко-
торая была посещена последней. Для реализации такого правила выбора наиболее удоб-
ной структурой хранения множества открытых вершин является стек: открываемые вер-
шины складываются в стек в том порядке, в каком они открываются, а в качестве актив-
ной выбирается последняя вершина [9].
2.4.2 Поиск в ширину
Поиск в ширину – это классический метод решения задачи нахождения кратчайше-
го пути между двумя конкретными вершинами графа. Кратчайший путь – это такой путь,
соединяющий вершины графа, который обладает тем свойством, что никакой другой путь,
соединяющий эти вершины, не содержит меньшее число ребер. Поиск в глубину мало
пригоден для решения этой задачи, поскольку предлагаемый им порядок прохождения
графа не имеет отношения к поиску кратчайших путей, а поиск в ширину предназначен
как раз для достижения этой цели [12].
Итак, рассмотрим метод поиска в ширину. Отметим, что в рассмотренном в преды-
дущем разделе методе поиска в глубину чем позднее будет посещена вершина, тем рань-
ше она будет использована – точнее, так будет при допущении, что вторая вершина посе-
щается перед использованием первой. Это прямое следствие того факта, что просмотрен-
ные, но еще не использованные вершины скапливаются в стеке. Поиск в ширину, грубо
говоря, основывается на замене стека очередью [11].
Идея поиска в ширину состоит в том, чтобы посещать вершины в порядке их уда-
ленности от некоторой заранее выбранной или указанной стартовой вершины a. Иначе
говоря, сначала посещается сама вершина a, затем все вершины, смежные с a, то есть на-
ходящиеся от нее на расстоянии 1, затем вершины, находящиеся от a на расстоянии 2, и
далее по удаленности [9].
Рассмотрим алгоритм поиска в ширину с заданной стартовой вершиной a. Вначале
все вершины помечаются как новые. Первой посещается вершина a, она становится един-
ственной открытой вершиной. В дальнейшем каждый очередной шаг начинается с выбора
некоторой открытой вершины x. Эта вершина становится активной. Далее исследуются
ребра, инцидентные активной вершине. Если такое ребро соединяет вершину x с новой
вершиной y, то вершина y посещается и превращается в открытую. Когда все ребра, инци-
дентные активной вершине, исследованы, она перестает быть активной и становится за-
крытой. После этого выбирается новая активная вершина, и описанные действия повто-
ряются. Процесс заканчивается, когда множество открытых вершин становится пустым.
15
Основная особенность поиска в ширину, отличающая его от других способов обхо-
да графов, состоит в том, что в качестве активной вершины выбирается та из открытых,
которая была посещена раньше других. Именно этим обеспечивается главное свойство
поиска в ширину: чем ближе вершина к старту, тем раньше она будет посещена. Для реа-
лизации такого правила выбора активной вершины удобно использовать для хранения
множества открытых вершин очередь – когда новая вершина становится открытой, она
добавляется в конец очереди, а активная выбирается в ее начале [9].
Оба метода поиска в графе – в глубину и в ширину могут быть использованы для
нахождения пути между фиксированными вершинами a и b. Достаточно начать поиск в
графе с вершины a и вести его до момента посещения вершины b. Преимуществом поиска
в глубину является тот факт, что в момент посещения вершины b стек содержит последо-
вательность вершин, определяющую путь из a в b. Это становится очевидным, если отме-
тить, что каждая вершина, помещаемая в стек, является смежной с предыдущей. Однако
недостатком поиска в глубину является то, что полученный таким образом путь в общем
случае не будет кратчайшим путем из a в b. От этого недостатка свободен метод нахожде-
ния пути, основанный на поиске в ширину [11].
2.4.3 Кратчайшие пути
В этом и 3 последующих разделах будем рассматривать ориентированные графы
G=(V,E), дугам которых приписаны веса. Это значит, что каждой дуге (u,v) поставлено в
соответствие некоторое вещественное число a(u,v), называемое весом данной дуги. Пола-
гаем a(u,v)=∞, если дуга (u,v) не существует.
Под длиной пути будем понимать сумму весов дуг, из которых состоит путь. Длину
кратчайшего пути будем обозначать d(s,t) и называть расстоянием от s до t. Если не
существует ни одного пути из s в t, то полагаем d(s,t)=∞.
Введем еще одно ограничение. Путь веса дуг будут только положительными значе-
ниями. Так как при существовании дуг с отрицательными весами длина кратчайшего пути
между парой вершин становится неопределенной, исходя из возможности неоднократного
включения таких дуг в путь.
Зная расстояние между парой вершин, можно легко определить кратчайший путь.
Так как для двух произвольных вершин s и t (s≠t) существует такая вершина v, что
d(s,t)=d(s,v)+d(v,t). Этим свойством обладает и предпоследняя вершина в кратчайшем пути
от s к t. Следовательно, определяя таким образом предпоследнюю вершину, можно пройти
от конца кратчайшего пути к его началу [11].
Большинство известных алгоритмов нахождения расстояния между двумя верши-
нами s и t можно описать следующей последовательностью действий.
1) При заданной матрице весов дуг A[u,v], вычисляем некоторые верхние ограниче-
ния D[v] на расстояния от s до всех вершин v.
2) Каждый раз, когда выясняется, что D[u]+A[u,v]<D[v], улучшаем оценку
D[v]=D[u]+A[u,v].
3) Процесс заканчивается, когда дальнейшее улучшение ни одного из ограничений
не возможно. Значение каждой D[u] получается равным расстоянию d(s,u). Вершину s в
данном случае называют источником.
Алгоритм нахождения расстояния от источника до всех вершин, реализующий вы-
шеизложенные действия в общем случае (при отсутствии контуров с отрицательной дли-
ной) называется методом Форда-Беллмана [13].
16
2.4.4 Алгоритм Дейкстры поиска кратчайшего пути
Алгоритм Дейкстры решает задачу нахождения кратчайших путей для единствен-
ного источника на ориентированных графах, имеющих неотрицательные веса. Он основан
на методе поиска в ширину.
Работу алгоритма Дейкстры можно описать следующей последовательностью дей-
ствий:
1) начинаем поиск путем помещения источника в просмотренную зону;
2) добавляем на каждом шаге одно ребро, дающее кратчайший путь из источника в
вершину, не включенную в просмотренную зону; то есть вершины добавляются в про-
смотренную зону в порядке возрастания их удаленности от источника.
Таким образом, чтобы найти кратчайший путь от s к t с помощью алгоритма Дейк-
стры, достаточно начать поиск с вершины s и закончить его, когда вершина t добавится в
очередь [12].
2.4.5 Алгоритм обхода препятствий А*
Предлагаемый алгоритм обхода препятствий основан на алгоритме Дейкстры. В
англоязычной литературе он называется алгоритмом A* («а»-звездочка) [14, 15].
Алгоритм реализуется в ряде предположений:
1) карта разбита на квадратные части, называемыми клетками (ячейками);
2) каждая клетка имеет несколько показателей:
• стоимость прохождения по этой клетке,
• предыдущая клетка – клетка, из которой пришли в эту клетку,
• статус клетки (нерассмотренная, граничная, отброшенная),
• оценка пройденного пути,
• оценка оставшегося пути;
3) имеются две клетки – начальная и конечная;
4) сосед клетки – клетка, в которую можно попасть из рассматриваемой за 1 шаг.
Общий принцип: на каждой итерации из всех граничных точек выбирается та, для
которой сумма уже пройденного пути и пути до конца по прямой является минимальной,
и от нее осуществляется дальнейшее продвижение.
Алгоритм итерационный. Опишем реализацию алгоритма пошагово. Начальные
данные: Start – начальная клетка, Finish – конечная клетка.
1 шаг. Помечаем Start как граничную точку.
2 шаг. Среди всех граничных точек находим Клетку1 – клетку с минимальной сум-
мой оценки пройденного пути g и оценки оставшегося пути h.
3 шаг. Для Клетки1 рассматриваем соседей. Если сосед имеет статус нерассмот-
ренного, то мы обозначаем его как граничную клетку, и указываем Клетку1 как предыду-
щую для него. Оценку g для соседа принимаем равной g+p, где p-стоимость прохождения
по клетке-соседу, а g – оценка пройденного пути для Клетки1. Оценка h для любой клетки
равна длине кратчайшего пути (количеству ячеек на пути по прямой от рассматриваемой
клетки до клетки Finish). Рассматриваемую Клетку1 помечаем как отброшенную.
4 шаг. Если на предыдущем шаге один из соседей оказался равен клетке Finish, то
путь найден. Если ни одного нового соседа не существует, то нет и пути.
5 шаг. Переход на шаг 2.
Алгоритм достаточно прост и в тоже время быстр. Он превосходит по скорости ал-
горитм Дейкстры (в общем случае) благодаря направленному поиску [14, 15].
17
2.5 Генетический алгоритм
Нейронные сети и генетические алгоритмы в настоящее время находят огромное
число разнообразных применений. Действительно, в любой области человеческой дея-
тельности есть задачи, для решения которых не существует определенного алгоритма или
существующие алгоритмы очень сложны и требуют значительных вычислительных затрат,
которые выходят за рамки возможностей современных ЭВМ. Нейронные сети и генетиче-
ские алгоритмы являются универсальным средством для решения подобных задач, а также
практически любых задач, которые возникают в человеческой деятельности [13].
В некоторых задачах, таких как прогнозирование, проектирование или распознава-
ние образов, нейронные сети стали уже привычным инструментом. Ниже приведены не-
которые из многочисленных способов использования нейронных сетей и генетических
алгоритмов в различных областях [16]:
• обслуживание кредитных карточек;
• медицинская диагностика;
• распознавание речи;
• обнаружение фальсификаций;
• анализ потребительского рынка;
• прогнозирование объема продаж и управление закупками;
• проектирование и оптимизация сетей связи;
• прогнозирование изменений котировок;
• управление ценами и производством;
• разработка месторождений;
• исследование факторов спроса;
• прогнозирование потребления энергии.
2.5.1 Естественный отбор в природе
Эволюционная теория утверждает, что каждый биологический вид целенаправлен-
но развивается и изменяется для того, чтобы наилучшим образом приспособиться к окру-
жающей среде. В процессе эволюции многие виды насекомых и рыб приобрели защитную
окраску, еж стал неуязвимым благодаря иглам, человек стал обладателем сложнейшей
нервной системы. Можно сказать, что эволюция – это процесс оптимизации всех живых
организмов. Рассмотрим, какими же средствами природа решает эту задачу оптимизации.
Основной механизм эволюции – это естественный отбор. Его суть состоит в том,
что более приспособленные особи имеют больше возможностей для выживания и раз-
множения и, следовательно, приносят больше потомства, чем плохо приспособленные
особи. При этом, благодаря передаче генетической информации (генетическому наследо-
ванию), потомки наследуют от родителей основные их качества. Таким образом, потомки
сильных индивидуумов также будут относительно хорошо приспособленными, а их доля в
общей массе особей будет возрастать. После смены нескольких десятков или сотен поко-
лений средняя приспособленность особей данного вида заметно возрастает [16].
Чтобы сделать понятными принципы работы генетических алгоритмов, поясним
также, как устроены механизмы генетического наследования в природе. В каждой клетке
любого животного содержится вся генетическая информация этой особи. Эта информация
записана в виде набора очень длинных молекул ДНК (дезоксирибонуклеиновая кислота).
Каждая молекула ДНК – это цепочка, состоящая из молекул нуклеотидов четырех типов,
обозначаемых А, T, C и G. Собственно, информацию несет порядок следования нуклеоти-
дов в ДНК. Таким образом, генетический код индивидуума – это просто очень длинная
строка символов, где используются всего 4 буквы. В животной клетке каждая молекула
18

ДНК окружена оболочкой – такое образование называется хромосомой. Каждое врожден-
ное качество особи (цвет глаз, наследственные болезни, тип волос и т. д.) кодируется оп-
ределенной частью хромосомы, которая называется геном этого свойства. Например, ген
цвета глаз содержит информацию, кодирующую определенный цвет глаз. Различные зна-
чения гена называются его аллелями.
При размножении животных происходит слияние двух родительских половых кле-
ток и их ДНК взаимодействуют, образуя ДНК потомка. Основной способ взаимодейст-
вия – кроссовер (cross-over – скрещивание). При кроссовере ДНК предков делятся на две
части, а затем обмениваются своими половинками. При наследовании возможны мутации
из-за радиоактивности или других влияний, в результате которых могут измениться неко-
торые гены в половых клетках одного из родителей. Измененные гены передаются потом-
ку и придают ему новые свойства. Если эти новые свойства полезны, они, скорее всего,
сохранятся в данном виде – при этом произойдет скачкообразное повышение приспособ-
ленности вида [
16].
2.5.2 Понятие и особенности генетического алгоритма
Пусть дана некоторая сложная функция (целевая функция), зависящая от несколь-
ких переменных, и требуется найти такие значения переменных, при которых значение
функции максимально. Задачи такого рода называются задачами оптимизации и встреча-
ются на практике очень часто.
Генетический алгоритм – это простая мо-
дель эволюции в природе, реализованная в виде
компьютерной программы. В нем используются
как аналог механизма генетического наследова-
ния, так и аналог естественного отбора. При этом
сохраняется биологическая терминология в упро-
щенном виде. Вот как моделируется генетическое
наследование:
• хромосома – вектор (последова-
тельность) из нулей и единиц. Каж-
дая позиция (бит) называется геном;
• индивидуум (генетический код) –
набор хромосом, вариант решения
задачи;
• кроссовер – операция, при которой
две хромосомы обмениваются
своими частями;
• мутация – случайное изменение од-
ной или нескольких позиций в
хромосоме.
Чтобы смоделировать эволюционный про-
цесс, сгенерируем вначале случайную популя-
цию – несколько индивидуумов со случайным на-
бором хромосом (числовых векторов). Генетиче-
ский алгоритм имитирует эволюцию этой популя-
ции как циклический процесс скрещивания индивидуумов и смены поколений.
Создание начальной поп
у
л
яции
Ск
р
ещивание
М
у
тация
Отбо
р
Ответ
Изменение при-
способленности
Рис. 2.8 – Блок-схема работы
генетического алгоритма
высокое
низкое
Жизненный цикл популяции – это несколько случайных скрещиваний (посредст-
вом кроссовера) и мутаций, в результате которых к популяции добавляется какое-то коли-
чество новых индивидуумов. Отбор в генетическом алгоритме – это процесс формирова-
19
ния новой популяции из старой, после чего старая популяция погибает. После отбора к
новой популяции опять применяются операции кроссовера и мутации, затем опять проис-
ходит отбор, и так далее (рис. 2.8).
Отбор в генетическом алгоритме тесно связан с принципами естественного отбора
в природе. Приспособленность индивидуума – значение целевой функции на этом инди-
видууме. Популяция следующего поколения формируется из наиболее приспособленных
особей. Чем больше приспособленность индивидуума, тем больше вероятность его уча-
стия в кроссовере, то есть размножении.
Таким образом, модель отбора определяет, каким образом следует строить популя-
цию следующего поколения. Как правило, вероятность участия индивидуума в скрещива-
нии берется пропорциональной его приспособленности. Часто используется так называе-
мая стратегия элитизма, при которой несколько лучших индивидуумов переходят в сле-
дующее поколение без изменений, не участвуя в кроссовере и отборе. В любом случае ка-
ждое следующее поколение будет в среднем лучше предыдущего. Когда приспособлен-
ность индивидуумов перестает заметно увеличиваться, процесс останавливают и в качест-
ве решения задачи оптимизации берут наилучшего из найденных индивидуумов [16].
Итак, если на некотором множестве задана сложная функция от нескольких пере-
менных, то генетический алгоритм – это программа, которая за разумное время находит
точку, где значение функции достаточно близко к максимально возможному. Выбирая
приемлемое время расчета, мы получим одно из лучших решений, которые вообще воз-
можно получить за это время.
2.5.3 Алгоритм решения задачи коммивояжера
Рассмотрим применение генетических алгоритмов в классической задаче комми-
вояжера (TSP – travelling salesman problem). Суть задачи состоит в том, чтобы найти крат-
чайший замкнутый путь обхода нескольких городов, заданных своими координатами.
Оказывается, что уже для 30 городов поиск оптимального пути представляет собой слож-
ную задачу, побудившую развитие новых различных методов (в том числе нейросетей и
генетических алгоритмов).
Каждый вариант решения такой задачи – это числовая строка, где на j-ом месте
стоит номер j-ого по порядку обхода города. Таким образом, в этой задаче столько пара-
метров, сколько городов в сети, причем не все комбинации значений допустимы. Естест-
венно, первой идеей является полный перебор всех вариантов обхода. Но такой подход к
решению задачи абсолютно невозможен при современных ЭВМ. Если в задаче все города
связаны с каждым из остальных, то количество разных вариантов решения задачи (N−1)!/2,
где N – количество городов в сети. При N=30 число вариантов решения 4,4×10
30
. Для пе-
ребора этих вариантов понадобится много времени! И это только при 30 городах, когда
как в практике задачи такого рода насчитывают сотни, и даже тысячи городов. В таких
ситуациях на помощь приходят генетические алгоритмы, которые, хотя и не гарантируют
нахождение оптимального решения, но позволяют найти одно из приемлемых решений
задачи [16].
Построение генетического алгоритма начинается с конструирования двоичной
хромосомы, представляющей возможные решения этой задачи. Традиционно генетиче-
ские алгоритмы используют для этого двоичные строки фиксированной длины. Предпо-
ложим, что задана сеть из 4-х городов, для кодирования каждого из которых понадобится
2 бита. Таким образом, хромосома будет иметь длину 1 байт. Например: «01_10_11_00».
Если следовать справа налево, то данная хромосома предполагает маршрут 0-3-2-1.
Очевидно, что такой подход к построению хромосомы не из лучших, потому что может
20
