Koren B., Vuik K. (Editors) Advanced Computational Methods in Science and Engineering
Подождите немного. Документ загружается.


On Numerical Issues in Time Accurate Laminar Reacting Gas Flow Solvers
G
j
= 10
9
m
j
ρ
j
S
∑
s=1
R
S
s
χ
js
, (7)
with m
j
the molecular mass of solid species j and
ρ
j
the density of solid species j.
3 Chemistry models
Numerical simulations presented in sections 4.2.1 and 6 are done for the CVD of
silicon from silane according to one of the two reaction models presented in this sec-
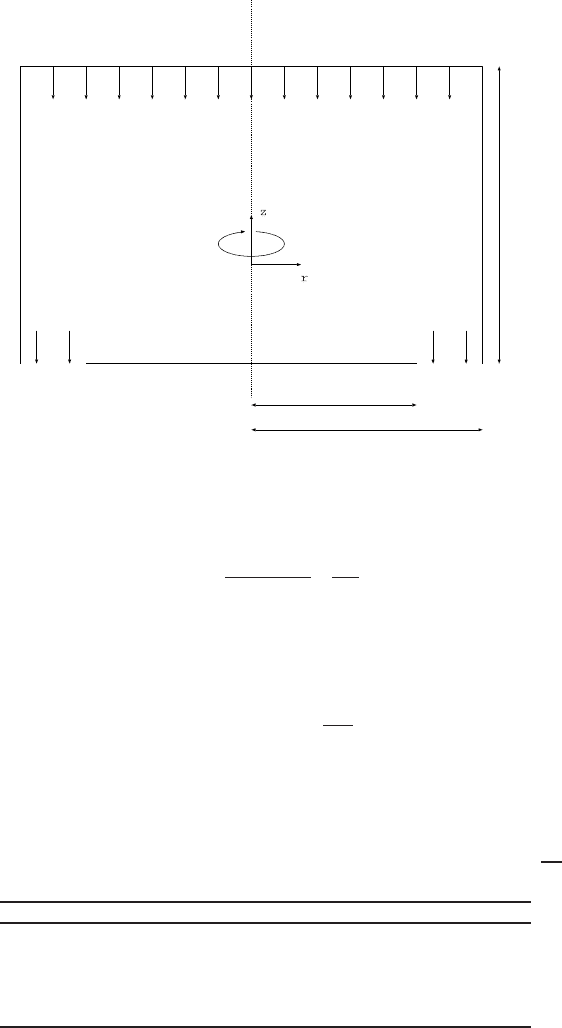
tion. For all simulations the reactor configuration is identical. Its geometry and the
matching boundary conditions are shown in Figure 3. As computational domain one
half of the (r-z) plane is taken. From the top a gas-mixture, consisting of 0.1 mole%
silane diluted in helium, enters the reactor with a uniform temperature T
in
= 300 K
and velocity u
in
= 0.1
m
s
. In the hot region above the susceptor with temperature
T
s
= 1000 K the reactive gas silane decomposes into silylene and hydrogen. This
first gas phase reaction initiates a chain of gas phase reactions, and the formation of
solid species on the wafer surface. In Section 3.1 a chemistry model consisting of 7
species and 5 gas phase reactions without surface chemistry is presented, whereas
in Section 3.2 we comprehensively describe the classical model as published by
Coltrin and coworkers [4], which includes 17 gas species, 26 gas phase reactions
and 14 surface reactions.
Further, in the processes considered in the present paper, silane and the formed
reactive intermediates are highly diluted in the inert carrier gas helium. Therefore,
it is justified to assume that the velocity, temperature, density and pressure fields
are in steady state and not influenced by the transient chemistry. Since the focus of
this study is on solving the species equations (1), we compute these fields using the
software of Kleijn [15]. Buoyancy has not been accounted for in these simulations.
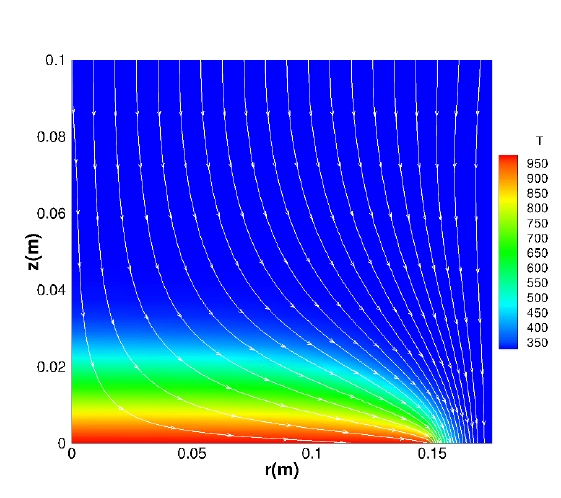
In Figure 3 the streamlines and temperature field are shown.
3.1 Chemistry model I: 7 species and 5 gas phase reactions
The 7 species and 5 gas phase reactions chemistry model has also been used in
[20]. The 5 reactions are listed in Table 1, in which all reactive species, except
for the carrier gas helium He, can also be found. Note that for this model only 6
nonlinearly and stiffly coupled species equations (1) have to be solved, because the
mass fraction of He can be computed via the property that all mass fraction should
add up to one. The reaction terms in eq. (1) are constructed as in eqs. (3) and (5), of
which the fit parameters can be found in Table 1. The backward rates are computed
selfconsistently from
53
S. van Veldhuizen, C. Vuik, and C.R. Kleijn
θ
susceptor
outflow
inflow
solid
wall
dT/dr = 0
v = 0
u = 0
T
in
=300 K f
SiH
4
= 0.001 f
He
= 0.999u
in
= 0.10 m/s
T
s
=1000 K u, v = 0
dT/dz = 0
dv/dz = 0
0.175 m
0.15 m
0.10 m
Fig. 2 Reactor geometry and boundary conditions.
k
g
backward
(T) =
k
g
forward
(T)
K
g
(T)
RT
P
0
∑
N
i=1
ν
ik
, (8)
with K
g
(T) the reaction equilibrium constants. To facilitate easy reproduction of the
solutions presented in the present paper, the reaction equilibrium constants are fitted
to a modified Arrhenius expression
K
g
(T) = A
eq
T
β
eq
e
−E
eq
RT
, (9)
with A
eq
,
β
eq
and E
eq
fit parameters which can be found in Table 1.
Table 1 Gas phase reaction mechanism and fit parameters for the 6 species/5 reactions model of
Section 3.1. The parameters
β
k
and
β
eq
are dimensionless, while E
k
and E
eq
have unit
kJ
mol
. The
units of A
k
and A
eq
depend on the order of the reaction, but are expressed in units mole, m
3
and s.
Reaction A
k
β
k
E
k
A
k,eq
β
k,eq
E
k,eq
SiH
4
⇄ SiH
2
+ H
2
1.09×10
25
−3.37 256 6.85×10
5
0.48 235
Si
2
H
6
⇄ SiH
4
+ SiH
2
3.24×10
29
−4.24 243 1.96×10
12
−1.68 229
Si
2
H
6
⇄ H
2
SiSiH
2
+ H
2
7.94×10
15
0 236 3.70×10
7
0 187
SiH
2
+ Si
2
H
6
⇄ Si
3
H
8
1.81×10
8
0 0 1.36×10
−12
1.64 −233
2SiH
2
⇄ H
2
SiSiH
2
1.81×10
8
0 0 2.00×10
−7
0 −272
54
On Numerical Issues in Time Accurate Laminar Reacting Gas Flow Solvers
Fig. 3 Streamlines and temperature field in Kelvin for the right half part of the reactor illustrated
in Figure 3.
3.2 Chemistry model II: 17 species and 26 gas phase reactions
The other test case in this study, is the same CVD process of silicon from silane, now
modeled according to the classical 17 species and 26 reactions chemistry model for
this process as published by Coltrin and coworkers [4]. In this model the decom-
position of silane into silylene and hydrogen, initiates a chain of 25 homogeneous
gas phase reactions leading to the (de)formation of 14 silicon containing gas phase
species. Again, the reaction terms in eq. (1) are constructed as in eqs. (3) and (5).
The backward rates are computed selfconsistently from eqs. (8) and (9). The 26
reactions and the fit parameters needed in eqs. (5) and (9) are listed Table 2.
Each of the silicon containing species may diffuse towards and react at the sus-
ceptor. In this model it is assumed that film growth is due to irreversible, unimolecu-
lar decomposition reactions of these species at the surface, leading to the deposition
of solid silicon atoms and the desorption of gaseous hydrogen according to:
Si
n
H
2m
R
S
Si
n
H
2m
−→ n Si (s)+ m H
2
(g), (10)
Si
n
H
2m+1
R
S
Si
n
H
2m+1
−→ n Si (s)+ m H
2
(g) + H (g), (11)
55
S. van Veldhuizen, C. Vuik, and C.R. Kleijn
Table 2 Fit parameters for the forward reaction rates (5) and gas phase equilibria constants (9) for
the benchmark problem. The parameters
β
k
and
β
eq
are dimensionless, while E
k
and E
eq
have unit
kJ
mol
. The units of A
k
and A
eq
depend on the order of the reaction, but are expressed in units mole,
m
3
and s.
Reaction A
k
β
k
E
k
A
k,eq
β
k,eq
E
k,eq
SiH
4
⇋ SiH
2
+ H
2
1.09×10
25
−3.37 256 6.85×10
5
0.48 235
SiH
4
⇋ SiH
3
+ H 3.69 ×10
15
0.0 390 1.45×10
4
0.90 382
Si
2
H
6
⇋ SiH
4
+ SiH
2
3.24×10
29
−4.24 243 1.96×10
12
−1.68 229
SiH
4
+ H ⇋ SiH
3
+ H
2
1.46×10
7
0.0 10 1.75×10
3
−0.55 −50
SiH
4
+ SiH
3
⇋ Si
2
H
5
+ H
2
1.77×10
6
0.0 18 1.12×10
−6
2.09 −6
SiH
4
+ SiH ⇋ Si
2
H
3
+ H
2
1.45×10
6
0.0 8 1.82 ×10
−4
1.65 21
SiH
4
+ SiH ⇋ Si
2
H
5
1.43×10
7
0.0 8 1.49 ×10
−10
1.56 −190
SiH
2
⇋ Si + H
2
1.06×10
14
−0.88 189 1.23×10
2
0.97 180
SiH
2
+ H ⇋ SiH + H
2
1.39×10
7
0.0 8 2.05 ×10
1
−0.51 −101
SiH
2
+ H ⇋ SiH
3
3.81×10
7
0.0 8 2.56 ×10
−3
−1.03 −285
SiH
2
+ SiH
3
⇋ Si
2
H
5
6.58×10
6
0.0 8 1.75 ×10
−12
1.60 −241
SiH
2
+ Si
2
⇋ Si
3
+ H
2
3.55×10
5
0.0 8 5.95 ×10
−6
1.15 −225
SiH
2
+ Si
3
⇋ Si
2
H
2
+ Si
2
1.43×10
5
0.0 68 2.67×10
0
−0.18 59
H
2
SiSiH
2
⇋ Si
2
H
2
+ H
2
3.16×10
14
0.0 222 1.67×10
6
−0.37 112
Si
2
H
6
⇋ H
3
SiSiH + H
2
7.94×10
15
0.0 236 1.17×10
9
−0.36 235
H
2
+ SiH ⇋ SiH
3
3.45×10
7
0.0 8 1.42 ×10
−4
−0.52 −183
H
2
+ Si
2
⇋ Si
2
H
2
1.54×10
7
0.0 8 7.47 ×10
−6
−0.37 −216
H
2
+ Si
2
⇋ SiH + SiH 1.54×10
7
0.0 168 1.65×10
3
−0.91 180
H
2
+ Si
3
⇋ Si + Si
2
H
2
9.79×10
6
0.0 198 1.55×10
2
−0.55 189
Si
2
H
5
⇋ Si
2
H
3
+ H
2
3.16×10
14
0.0 222 1.14×10
6
0.08 210
Si
2
H
2
+ H ⇋ Si
2
H
3
8.63×10
8
0.0 8 3.43 ×10
−4
−0.31 −149
H + Si
2
⇋ SiH + Si 5.15×10
7
0.0 22 1.19×10
3
−0.88 29
SiH
4
+ H
3
SiSiH ⇋ Si
3
H
8
6.02×10
7
0.0 0 7.97 ×10
−16
2.48 −233
SiH
2
+ Si
2
H
6
⇋ Si
3
H
8
1.81×10
8
0.0 0 1.36 ×10
−12
1.64 −233
SiH
3
+ Si
2
H
5
⇋ Si
3
H
8
3.31×10
7
0.0 0 1.06 ×10
−14
1.85 −318
H
3
SiSiH ⇋ H
2
SiSiH
2
1.15×10
20
−3.06 28 9.58 ×10
−3
0.50 −50
where n = 1,2, or 3, and m = 0,1,2,3, or 4. The molar reaction rate R
S
i
for the
decomposition of gas species i is given as
R
S
i
=
γ
i
1 −
γ
i
2
P f
i
(2
π
m
i
RT
s
)
1
2
, (12)
where T
s
denotes the temperature of the wafer surface and f
i
is the species mole
fraction computed as
f
i
=
ω
i
m
m
i
. (13)
The sticking coefficient
γ
i
is equal to one for all silicon containing species, except
for
γ
Si
3
H
8
= 0,
γ
Si
2
H
6
= 0.537exp(
−9400
T
s
), and
γ
SiH
4
=
1
10
γ
Si
2
H
6
. (14)
56
On Numerical Issues in Time Accurate Laminar Reacting Gas Flow Solvers
There is some ambiguity as to which values of sticking coefficients were used in
[4]. The values of the sticking coefficients used in this paper are the ones from [15].
4 Numerical difficulties
A lot of time dependent numerical solvers follow the popular Method of Lines
(MOL) approach, in which space and time discretizations are considered separately.
The popularity of this approach is based on its simple concept, flexibility, the fact
that various discretizations can easily be combined and that nowadays many well
developed ODE methods exist.
Here, the spatial discretization of the stiff system of species equations (1) is done
in a Finite Volume (FV) setting, yielding a semi-discrete system
w
′
(t) = F(t,w(t)), t ≥ 0, (15)
with w(0) given. According to the MOL approach, fully discrete approximations are
obtained by applying a suitable time integration method with time step size
τ
for the
time levels t
n
= n
τ
,n = 1, 2,. ..
Stiffness in the reaction terms of eq. (1) requires implicit time integration of these
terms in order to maintain stability. In this section we summarize the results obtained
in [24], in which various ODE methods for reacting flow problems are compared. It
should be noted that if the computational costs of one time step is expensive, a time
integration method that needs more but computationally cheaper time steps can be
more efficient.
On the other hand, a natural property of species mass fractions and/or species
mass concentrations is their natural non-negativity. Of course, we want this prop-
erty to be conserved in both spatial and time discretization, as well as in the (time
accurate) solution. It appears that for time integration methods this natural property
is hard to be fulfilled for stiff problems. In Section 4.1 the conservation of non-
negativity is comprehensively described.
4.1 Positivity conservation of mass fractions
Conserving the natural non-negativity property of species concentrations is not eas-
ily maintained when integrating the species equations (1). Generally speaking, pos-
itivity should hold for
1. the mathematical model,
2. spatial discretization,
3. time integration, and,
4. iterative solvers.
57

S. van Veldhuizen, C. Vuik, and C.R. Kleijn
It can be shown that the mathematical model as presented in Section 2.1 and 2.2
preserves positivity [24]. Subsequently, we demand that neither spatial discretiza-
tion nor time integration should introduce wiggles or negative components into the
solution vector. Spatial discretization is done in a Finite Volume (FV) setting, in
which positivity is preserved since we use a hybrid scheme in which the fluxes are
approximated by central differences if possible, and by first order upwind if nec-
essary, see [18]. For details see, for instance, [14, 22, 24]. For time integration, on
the other hand, preserving positivity is certainly not easily guaranteed. Implicit time
integration gives rise to huge nonlinear systems, which are solved by iterative solu-
tion methods, such as Newton method. In the next sections we discuss positivity for
time integration, and on our strategies to maintain this property on the lower level
of iterative solvers.
4.1.1 Positive time integration
Definition 1. An ODE system w
′
(t) = F(t, w(t)), t ≥ 0, is called positive, or non-
negativity preserving, if w(0) ≥ 0 (component-wise) =⇒ w(t) ≥ 0, for all t > 0.
The next theorem provides a simple criterion on F(t, w(t)) to test whether the system
w
′
(t) = F(t,w(t)), t ≥ 0, is positive. For a proof we refer to [12].
Theorem 1. Suppose that F(t, w) is continuous and satisfies a Lipschitz condition
with respect to w. Then the system w
′
(t) = F(t, w(t)), t ≥ 0, is positive if and only if
for any vector w ∈ R
m
and all i = 1, ...,m, and t ≥ 0 yields
w ≥ 0 (componentwise), w
i
= 0 =⇒F
i
(t, w) ≥ 0. (16)
It is interesting to investigate positivity for semi-discrete systems. Consider, for
instance, the one dimensional linear advection-diffusion equation
∂
∂
t
u(x,t) +
∂
∂
x
(a(x,t)u(x,t)) =
∂
∂
x
d(x,t)
∂
∂
x
u(x,t)
, (17)
with periodic boundary conditions, and where a(x,t) is the space and time depen-
dent advection coefficient, and d(x,t) > 0 the space and time dependent diffusion
coefficient. Application of Theorem 1 shows that finite difference discretization by
means of central differences gives a positive semi-discretization if and only if the
cell P´eclet numbers, defined as ah/d, satisfy
max
x,t
|a(x,t)|h
d(x,t)
≤ 2. (18)
Discretizing the advection part by means of first order upwind, and second order
central differences for the diffusive part, gives an unconditionally positive semi-
discretization. The reaction terms (3) can be written in the production-loss form
¯
R
g
k
(t, w) = p(t, w) −L(t, w)w, (19)
58
On Numerical Issues in Time Accurate Laminar Reacting Gas Flow Solvers
where p(t,w) ≥ 0 (componentwise) is a vector and L(t, w) ≥ 0 (componentwise)
a diagonal matrix, whose components p
i
(t, w) and L
i
(t, w) are of polynomial type
with non-negative coefficients and can easily be found. Addition of reaction terms
according to eq. (3), which can be written in the production-loss form (19), to
the advection-diffusion eqn. (17) and applying Theorem 1 gives a positive semi-
discretization for the one dimensional advection-diffusion-reaction equation if and
only if p(t, w) ≥ 0, see also [12, Section I.7].
The one-dimensional results above are easily generalized to higher dimensions
and to FV schemes. Therefore, discretizing the species equations in space by means
of a hybrid FV scheme as introduced in [14, 22, 24], which uses the central differ-
ence scheme if possible and the first order upwind scheme if necessary, maintains
positivity. We remark that for higher order upwinding, such as, for example, third
order upwinding, positivity is not ensured for all step-sizes, see [12, Section I.7].
Definition 2. A time integration method w
n+1
=
ϕ
(w
n
) is called positive if for all
n ≥ 0 holds, w
n
≥ 0 =⇒w
n+1
≥0.
Positivity restricts the use of time integration methods. In this section we will
present results for non-linear systems w
′
(t) = F(t,w(t)). First, we start exploring
the positivity property for Euler Forward and Backward time integration.
4.1.2 Positivity for Euler Forward (EF) and Euler Backward (EB)
Suppose that the right hand side of the non-linear semi-discretization w
′
(t) =
F(t,w(t)) satisfies:
Condition 2 There is an
α
> 0, depending on F(t, w), such that for a time step
τ
holds: if
ατ
≤ 1, then w +
τ
F(t, w) ≥ 0 for all t ≥ 0 and w ≥0.
Provided that w
n
≥ 0, Condition 2 guarantees positivity for w
n+1
computed via
EF. For linear semi-discrete systems w
′
(t) = Aw(t) with entries A
i j
≥ 0 for i 6= j,
A
ii
≥ −
ζ
for all i and
ζ
> 0 fixed, Condition 2 is easily illustrated. Application of
Euler Forward to this systems gives a positive solution if 1 +
τ
A
ii
≥ 0 for all i. This
will hold if
ατ
≤ 1. To write down such an expression for
α
for eq. (1) is almost
undoable, because of the complicated structure of the chemical source terms.
Furthermore, assume that F(t,w(t)) also satisfies :
Condition 3 For any v ≥ 0,t ≥ 0 and
τ
> 0 the equation w = v +
τ
F(t,w), has a
unique solution w that depends continuously on
τ
and v.
According to the following theorem we have unconditional positivity for EB. The
proof is taken from [12].
Theorem 4. Condition 2 and 3 imply positivity for EB for any step size
τ
.
Proof. For given t,v and with a chosen
τ
, we consider the equation w = v+
τ
F(t, w)
and we call its solution w(
τ
). We have to show that v ≥ 0 implies w(
τ
) ≥ 0 for all
positive
τ
. By continuity it is sufficient to show that v > 0 implies w(
τ
) ≥ 0. This
59
S. van Veldhuizen, C. Vuik, and C.R. Kleijn
is true because if we assume that w(
τ
) > 0 for
τ
≤
τ
0
, except for the i
th
component
w
i
(
τ
0
) = 0, then 0 = w
i
= v
i
+
τ
0
F
i
(t, w(
τ
0
)). According to Condition 2 we have
F
i
(t, w(
τ
0
)) ≥ 0 and thus v
i
+
τ
0
F
i
(t, w(
τ
0
)) > 0, which is a contradiction.
Remark 1. Application of EB to the nonlinear semi-discretization w
′
(t) = F(t, w(t))
needs the solution of the nonlinear vector equation
w
n+1
−
τ
F(t
n
,w
n+1
) = w
n
. (20)
Theorem 4 ensures for every time step size
τ
positivity of the exact solution of (20).
In practice, however, the solution of (20) is approximated iteratively, and therefore,
it is not guaranteed to be positive. In Section 5.1 we present a class of projected
Newton methods to prevent this undesired behavior.
4.1.3 Positive time integration continued: general remarks
For reacting flow simulations, time integration schemes can only be unconditionally
positive if they are implicit, i.e., the severe stiffness in these problems rules out
explicit integration of the reaction terms. One might hope to find accurate higher
order methods with this unconditional positivity property. However, this hope is
dashed by the following result, due to Bolley and Crouzeix [1].
Theorem 5. Any unconditionally positive time integration method has order p ≤1.
For a proof we refer to [1]. The consequence is that the only well-known method
having unconditional positivity is EB. Finally, we remark that for higher order meth-
ods the need to preserve positivity may necessitate the use of impractically small
time steps.
To conclude, higher order methods are expected to integrate eq. (1) with small
time steps, which is not feasible for simulations over relatively long time frames.
The first order Euler Backward scheme is capable, from a theoretical point of view,
of taking large time steps, which are only bounded by the required accuracy. With
respect to accuracy, the first order consistency is a drawback.
Although higher order schemes suffer from severe positivity restrictions, we
compare three classes of higher order ODE methods with EB, in terms of efficiency.
The selection of these higher order ODE methods is based on properties like good
performance for diffusion-reaction problems, or on efficiency of the solver itself.
The results are presented in the next section.
4.2 Comparison of some stiff ODE methods
While on the one hand the intuitive meaning of stiffness is clear to computational
scientists, on the other hand a mathematical definition is missing. Following the
interpretation given in [12], we say that a PDE is stiff when implicit ODE methods
60

On Numerical Issues in Time Accurate Laminar Reacting Gas Flow Solvers
perform considerably better than explicit ODE methods. Certainly, this property also
depends on the eigenvalue distribution of the Jacobian matrix of F in eq. (15) and
on the smoothness of the solution.
As said before, a lot of research has been done in the field of ODE methods. The
result is that a huge amount of literature is available on time integration methods
for stiff problems, see for instance [10, 12]. In [24] we compared the uncondition-
ally stable and unconditionally positive Euler Backward method with the following
second order methods:
• Rosenbrock methods are linearly implicit Runge-Kutta methods for stiff ODEs,
which have proven to be effective for various stiff problems, see [10, 12]. The
second order Rosenbrock scheme ROS2, which depends on the choice of the
parameters b
2
and
γ
,
w
n+1
= w
n
+ b
1
k
1
+ b
2
k
2
k
1
=
τ
F(t
n
,w
n
) +
γτ
J
F
k
1
(21)
k
2
=
τ
F(t
n
+
α
21
τ
,w
n
+
α
21
k
1
) +
γ
21
τ
J
F
k
1
+
γτ
J
F
k
2
,
with coefficients b
1
= 1−b
2
,
α
21
=
1
2b
2
and
γ
21
= −
γ
b
2
, has been implemented. In
(21) J
F
is the Jacobian of F(t
n
,w
n
). ROS2 is second order consistent for arbitrary
γ
and b
2
6= 0, A-stable for
γ
≥
1
4
and L-stable if
γ
= 1 ±
1
2
√
2. By selecting for
γ
the larger value
γ
+
= 1 +
1
2
√
2, we have the property that R(z) ≥ 0, for z ∈ R
−
,
where R(z) is the stability function of ROS2. For diffusion-reaction problems,
which have a Jacobian with negative real eigenvalues, this property ensures a
positive solution. Adding advection introduces imaginary parts to the eigenval-
ues, such that positivity is no longer guaranteed. However, as has been experi-
enced in [26], the ROS2 scheme performs quite well with respect to positivity
for advection-diffusion-reaction problems. Although there is no explanation for
this unexpected behavior, it is conjectured that the property that R(z) ≥ 0 for all
z ∈ R
−
plays a role [26].
• Backward Differentiation Formulas (BDF) belong to the most widely used meth-
ods to solve stiff chemical reaction equations, due to their favorable stability
properties. The k-step BDF methods are implicit, of order k and defined as
k
∑
j=0
α
j
w
n+ j
=
τ
F(t
n+k
,w
n+k
), n = 0,1,.. ., (22)
which uses the k past values w
n
,.. .,w
n+k−1
to compute w
n+k
. Note that the most
advanced level is t
n+k
instead of t
n+1
. The 1-step BDF method is EB, whereas
the 2-step method is
3
2
w
n+2
−2w
n+1
+
1
2
w
n
=
τ
F(t
n+2
,w
n+2
). (23)
The BDF-1 and BDF-2 methods are A-stable, but for k > 2 they are A(
α
)-stable
and for k > 6 even unstable [9]. Remark that the first (k−1) approximations can-
61

S. van Veldhuizen, C. Vuik, and C.R. Kleijn
not be computed with the k-step BDF scheme, and should thus be obtained by
another scheme. Under Condition 2 and 3 we obtain positivity for BDF2 when-
ever
ατ
≤
1
2
, provided that w
1
is computed positively from w
0
. Remark that this
positivity condition is a factor 2 tighter than the condition for EF.
• IMEX Runge-Kutta Chebyshev methods (IRKC) are the IMEX extension of the
class of Runge-Kutta Chebyshev (RKC) methods, developed by Verwer et. al.
[25]. The class of explicit RKC schemes was designed to integrate moderately
stiff problems, for instance discretized diffusion, as computationally cheap as
possible. In [25] this class of methods was extended such that much stiffer prob-
lems can also be integrated efficiently. The exact description of the scheme is
rather spacious, and is therefore omitted here. In [24, 25] the scheme is compre-
hensively described, but it is worthwhile to remark that advection and diffusion
are integrated explicitly and the reaction terms implicitly. Two versions of IRKC
have been implemented; the IRKC(full) uses the CFL-condition to integrate ad-
vection and diffusion stably, see also [25]. The ‘on the fly’ version of IRKC,
called IRKC(fly), uses only stability conditions for diffusion. To conclude, for
this scheme no conditions are known to guarantee positivity, although we know
that the scheme is not unconditionally positive.
Details on the exact nonlinear solvers used for the simulations can be found in
[24]. Basically, a Newton method extended with an Armijo rule to enforce global
convergence has been implemented. Further, there is also the option to update the
Jacobian occasionally. In that case the Jacobian is only computed when it is neces-
sary to maintain a sufficient decrease in the Newton residual. For further details we
refer to [24]. The linear systems are solved by means of an LU factorization. It has
to be remarked that direct linear solvers are only feasible when a suitable ordering
of unknowns is used, see [24].
4.2.1 Numerical results
The ODE methods presented in the above section have been tested on the bench-
mark problem of Kleijn [15]. Recall that the chemistry model of this CVD process
consists of 17 different species and 26 reactions. Furthermore, surface chemistry as
described in Section 3.2 is included. The reactor configuration for all simulations
has been illustrated in Figure 3.
The simulation runs from the the instant that the reactor is completely filled with
helium carrier gas and a mixture of helium and silane starts to enter the reactor,
until steady state. The spatial computational grid consists of 35 equidistant grid
points in radial direction, and 32 non-equidistant grid points in axial direction. The
grid spacing in axial direction gradually decreases towards the wafer surface. In our
experiments steady state is assumed to be obtained when for a certain time step t
n
the inequality
kw
n+1
−w
n
k
2
kw
n
k
2
≤10
−6
, (24)
62
