Mrinal K Pal. Power system stability
Подождите немного. Документ загружается.

STABILITY BASICS
2-9
The State Variables of a Dynamic System
The time-domain analysis of dynamic systems utilizes the concept of the state of a system. The
state of a system is a set of numbers or variables (state variables), such that a knowledge of these
along with the input functions (control forces) and the equations describing the dynamics of the
system, is sufficient to completely determine the future behavior (state and output) of the system.
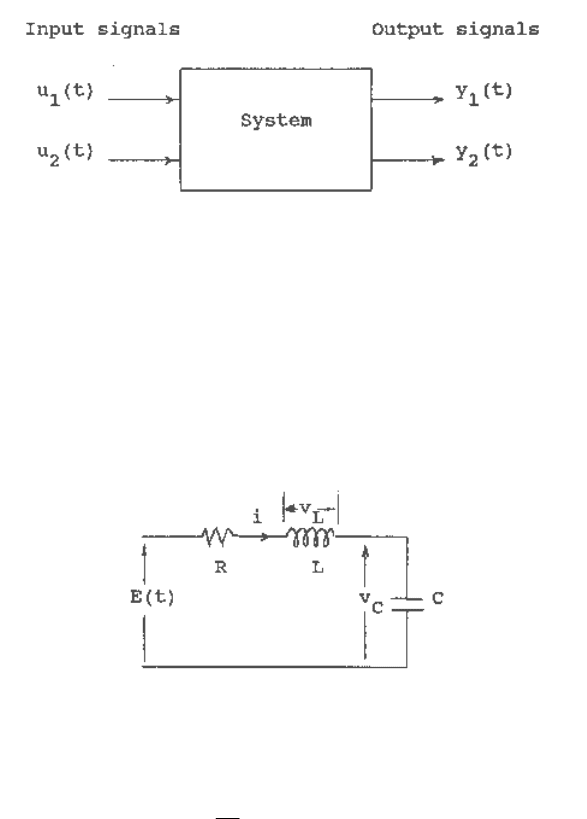
Consider the system shown in Figure 2.5, where
)(
1
ty and )(
2
ty are the output signals and )(
1
tu
and
)(
2
tu are the input signals. A set of state variables ),,,(
21 n
xxx L for the system shown in
Figure 2.5 is a set such that a knowledge of the initial values of the state variables
))(,),(),((
oo2o1
txtxtx
n
L at the initial time
o
t , and of the input signals
)(
1
tu
and
)(
2
tu
for t ≥
o
t , suffices to determine the future values of the outputs and state variables.
Fig. 2.5 Block diagram of a dynamic system.
The concept of a state variable description of a system can be illustrated in terms of the RLC
circuit shown in Figure 2.6. The number of state variables chosen to represent a system should
not exceed the minimum number required so as to avoid redundancy. The state of the system in
Figure 2.6 may be described in terms of a set of state variables
),(
21
xx where
1
x is the capacitor
voltage )(tv
C
and
2
x is the current i(t) flowing through the circuit. (For a passive RLC network,
the number of state variables required is equal to the number of independent energy storage
elements.)
Fig. 2.6 An RLC circuit.
Applying Kirchhoff's voltage law to the circuit of Figure 2.6,
)(tEv
dt
di
LRi
C
=++ (2.22)
Also

STABILITY BASICS
2-10
dt
dv
Ci
C
= (2.23)
The output, v
L
, is given by
dt
di
Lv
L
=
(2.24)
We may rewrite (2.22) and (2.23) in terms of the state variables
(
)
)(
1
tvx
C
=
and
()
)(
2
tix
=
as
follows:
2
1
1
x
Cdt
dx
=
(2.25)
)(
11
)(
11
2121
2
tu
L
x
L
R
x
L
tE
L
x
L
R
x
Ldt
dx
+−−=+−−=
(2.26)
The output signal is then
)()(
21
2
tuxRx
dt
dx
Ltyv
L
+−−===
(2.27)
Utilizing equations (2.25) and (2.26) and the initial conditions of the network represented by
()
)(,)(
o2o1
txtx , we may determine the system's future behavior and its output.
Consider the spring-mass-damper system shown in Figure 2.7.
Fig. 2.7 A spring-mass-damper system.
The differential equation describing the behavior of the system can be written as
)(
2
2
tuyK
dt
dy
f
dt
yd
M =++ (2.28)
A set of state variables sufficient to describe this system is the position and velocity of the mass.
Therefore, we can define a set of state variables as
),(
21
xx where
)()(
1
tytx = , and
dt
tdy
tx
)(
)(
2
=
Problem
Write the state equations for the system shown in Figure 2.7.

STABILITY BASICS
2-11
The state variables which describe a system are not a unique set. Several alternative sets of state
variables may be chosen. A good choice is a set of state variables which can be readily
measured.
The state vector differential equation
A dynamic system can be described by a set of first-order differential equations written in terms
of the state variables. The first-order differential equations of a linear system may be written in a
general form as
mnmnnnnnnn
mmnn
mmnn
ububxaxaxax
ububxaxaxax
ububxaxaxax
++++++=
++++++=
+
+
+
+
+
+=
LL
&
LLLLL
LL
&
LL
&
112211
212122221212
111112121111
(2.29)
where dtdxx /=
&
, and some of the coefficients
ijij
ba and may be zero.
This set of simultaneous differential equations may be written in a matrix form as
+
=
mnmnn
m
m
nnnnn
n
n
n
u
u
u
bbb
bbb
bbb
x
x
x
aaa
aaa
aaa
x
x
x
M
L
MMM
L
L
M
L
MMM
L
L
&
M
&
&
2
1
21
22221
11211
2
1
21
22221
11211
2
1
or
uBxAx
+
=
&
(2.30)
x is the vector of the state variables and u is the vector of input signals. The matrix A is an n × n
matrix and
B is an n × m matrix. The vector matrix differential equation relates the rate of
change of the state of the system to the state of the system and the input signals. The matrix
A is
also known as the coefficient matrix or the system matrix. In general, the outputs of a linear
system may be related to the state variables and the input signals by the vector matrix equation
uDxCy
+
=
(2.31)
where
y is the set of output signals expressed in a column vector form.
The nth order linear differential equation
)(
01
2
2
2
1
1
1
tuxa
dt
dx
a
dt
xd
a
dt
xd
a
dt
xd
n
n
n
n
n
=+++++
−
−
−
L
can be reduced to the form of n first-order state equations as follows:
Defining the state variables as
1
1
2
2
321
,,,,
−
−
====
n
n
n
dt
xd
x
dt
xd
x
dt
dx
xxx
L
the n − 1 first-order differential equations are
nn
xxxxxx
=
=
=
−13221
,,,
&
L
&&

STABILITY BASICS
2-12
The nth equation is
)(
12110
tuxaxaxa
dt
xd
x
nn
n
n
n
+−−−−==
−
L
&
so that
)()(
1
0
0
0
0
10000
01000
00100
00010
13210
tutu
aaaaa
n
BAxxx +=
+
−−−−−
=
−
M
L
L
MM
L
L
L
&
The output is
[
]
)()(0001)()(
1
tttxtx Cxx
=
== L
The solution of the state vector differential equation (2.30) may be obtained in a manner similar
to that used for solving a first-order differential equation.
As in the case of an nth order differential equation, the solution to the linear unforced system
xAx
=
&
(2.32)
will describe the character of the response of the system. As before, the solution to equation
(2.32) is of exponential form. If we let
t
λ
ε
ex = and substitute into (2.32), we have
tt
λλ
εελ
eAe =
or
eAe
=
λ
(2.33)
Equation (2.33) may be written as
[]
0eAI
=
−
λ
(2.34)
where
I is the identity matrix and 0 equals the null vector. Equation (2.34) has a nontrivial
solution if, and only if, the determinant of the matrix
[
]
AI
−
λ
vanishes, i.e., if
0=− AI
λ
(2.35)
The equation resulting from the evaluation of this determinant is the characteristic equation. It is
a polynomial in
λ
. For an nth order system the equation will have n roots, called the
characteristic roots or the eigenvalues of the system. The stability of the system may be readily
ascertained from an examination of the characteristic roots.
Problems
1. Show that the characteristic equation of the spring-mass-damper system shown in Figure
2.7 is the same whether derived from equation (2.28) or from the state equations describing
the system.
2.
Convert the following set of first-order equations (state equations) into a second-order
differential equation and show that the characteristic equations in both representations are
the same.
STABILITY BASICS
2-13
2221212
2121111
xaxax
xaxax
+=
+
=
&
&
The choice of state variables describing a system is not unique. For example, another set of state
variables
z could be used to describe the system given by (2.30) where z is related to x by the
relationship
zTx
=
(2.36)
where
T is the transformation matrix. In order for the transformation to be reversible T must be
non-singular.
Substituting (2.36) into (2.30), we have
uBTzTATz
11 −−
+=
&
(2.37)
Equation (2.37) describes the same system as (2.30) and the characteristic roots are not altered in
the transformation (verify this).
If the system is unstable (i.e. some of the characteristic roots of
A have positive real parts) or has
unacceptable transient response, the system can be stabilized and the performance improved by
utilizing feedback of the state variables. If state variable feedback is used so that
xHu
−
=
,
where
H is the feedback matrix, equation (2.30) reduces to
[
]
xAxHBAx
1
=
−
=
&
(2.38)
The elements of the matrix
H can be so chosen that the modified system given by equation (2.38)
will have the desired performance.
Solution of the equation xAx =
&
The solution is of the exponential form given by
t
λ
ε
ex = (2.39)
As noted earlier,
λ
is obtained by solving equation (2.35), which is a polynomial in
λ
. For an nth
order system the equation has n roots called the characteristic roots.
The vector
e is obtained from a solution of equation (2.33). The vector e obtained for each
λ
is
called a characteristic vector or an eigenvector of the system. It may be noted that equation
(2.33) is satisfied by multiplying the vector
e by any constant k. Therefore, the absolute values of
the elements of the eigenvectors are not determined. Only the direction of each eigenvector is
unique.
The complete solution of the equation
xAx
=
&
can therefore be written as, assuming that the
roots are distinct,
t
nn
tt
n
kkkt
λ
λλ
εεε
eeex +++= L
21
2211
)( =
∑
=
n
i
i
t
i
k
i
1
λ
ε
e
(2.40)
where k
1
, k
2
, etc. are arbitrary constants to be determined from given initial conditions; e
1
, e
2
, etc.
are the eigenvectors corresponding to the eigenvalues
λ
1
,
λ
2
, etc.
Equation (2.40) can be written in matrix form as

STABILITY BASICS
2-14
kQMx )()( tt
=
(2.41)
where
[
]
n
eeeM L
21
=
(2.42)
is a matrix composed of the eigenvectors
e
1
, e
2
, etc. called the modal matrix,
=
t
t
t
n
t
λ
λ
λ
ε
ε
ε
O
2
1
)(Q
and
=
n
k
k
k
M
2
1
k
If the initial value of
x is given by
o
x then
kMx
=
o
from which
o
1
xMk
−
=
Therefore, the solution can be written as
o
1
)()( xMQMx
−
= tt (2.43)
Example
We will obtain the solution of the second-order equation
x
dt
xd
2
2
2
ω
−= (2.44)
by the above method.
Equation (2.44) can be written in state space form as
−
=
2
1
2
2
1
0
10
x
x
x
x
ω
&
&
(2.45)
where
211
, xxxxx
=
=
=
&&
The eigenvalues of the system are
ω
λ
j
±
=
2,1
We obtain the eigenvectors as follows
−
=
21
11
2
21
11
0
10
e
e
e
e
j
ω
ω

STABILITY BASICS
2-15
from which
11
2
21
2111
eej
eej
ωω
ω
−=
=
with
ω
jee ==
2111
,1
For the second eigenvector
−
=
−
22
12
2
22
12
0
10
e
e
e
e
j
ω
ω
from which
12
2
22
2212
eej
eej
ωω
ω
−=−
=
−
with
ω
jee −==
2212
,1
Therefore, the modal matrix is
−
=
ωω
jj
11
M
and
−
=
−
ω
ω
2/2/1
2/2/1
1
j
j
M
If
=
0
o1
o
x
x
then the solution is, from equation (2.43),
−
=
−
=
−
−
=
−
−
tx
tx
x
x
jj
x
j
j
jj
x
x
tj
tj
tj
tj
ωω
ω
ε
ε
ωω
ω
ω
ε
ε
ωω
ω
ω
ω
ω
sin
cos
11
2
1
02/2/1
2/2/111
o1
o1
o1
o1
o1
2
1
from which
txxtxx
ω
ω
ω
sin,cos
o12o11
−
=
=
Problem
Show that if the initial condition vector is
=
o2
o1
o
x
x
x
the solution is of the form
)cos(
1
φ
ω
−
= tAx
STABILITY BASICS
2-16
Since the modes of a system response, i.e., whether it is oscillatory, damped or undamped, etc.,
are determined by the eigenvalues, the eigenvalues are often referred to as the system modes.
The relative impact of a particular mode on a system variable depends on the relative magnitude
of the element of the corresponding eigenvector. For this reason, the eigenvectors can be
considered as describing the mode shapes.
From equation (2.43) it should be clear that the overall impact of the various modes on the
system response depends on the eigenvectors as well as the initial condition. For example, if the
initial perturbation is in the direction of one of the eigenvectors, say the eigenvector
corresponding to the eigenvalue
λ
1
, i.e., if
α
=
M
31
21
11
o
e
e
e
x
then
α
=
−
M
0
0
1
o
1
xM , since IMM =
−1
and
=
=
MMM
t
tt
e
e
x
x
1
11
21
11
2
1
0
λ
λλ
εα
εαεα
M
Therefore, all the modes except the one corresponding to
λ
1
, are absent.
An alternative derivation of equation (2.43)
If equation (2.33) is written for each eigenvalue and the corresponding eigenvector and
combined, we have
MAΛM
=
(2.46)
where M is the modal matrix as defined previously and
Λ
is a diagonal matrix composed of the
eigenvalues, i.e.,
(
)
L,,diag
21
λ
λ
=Λ
From (2.46)
ΛMAM =
−1
(2.47)
If we now write equation xAx =
&
in terms of another set of variables z using the transformation
zMx
=
(2.48)
we have
zMAzM
=
&
from which
zΛzMAMz ==
−1
&
(2.49)
STABILITY BASICS
2-17
The variables in equation (2.49) are completely decoupled. The solution to equation (2.49) is
therefore
o
)( zQz t
=
(2.50)
where the matrix Q(t) is as defined earlier; z
o
is obtained from equation (2.48) as
o
1
o
xMz
−
=
which yields
o
1
)( xMQMzMx
−
== t
(2.43)
Note that by definition
L++++=
!3!2
3322
tt
t
t
AA
AI
A
ε
t
t
t
t
tt
tt
Λ
ΛΛ
ΛIQ
ε
ε
ε
ε
λ
λ
λ
=++++=
=
∴
L
O
!3!2
)(
3322
3
2
1
t
tt
tt
A
M
ΛΛ
ΛIMMMQ
ε
=
++++=
∴
−− 1
3322
1
!3!2
)( L
Therefore the solution (2.43) can also be written as
o
xx
At
ε
= (2.51)
Equation (2.51) also follows directly from the solution of the first-order equation by analogy.
The matrix
tA
ε
is known as the fundamental or transition matrix, usually denoted by )(tφ .
It can be shown that the solution to the equation (2.30) is
∫
−
+=
t
tt
dt
o
)(
o
)()(
ττεε
τ
uBxx
AA
(2.52)
Liapunov’s Direct Method of Stability Analysis
We will now review the so-called Liapunov’s direct method of stability analysis.
A single valued function V(x) is said to be positive (negative) definite in some neighborhood of
the origin, if V(0) = 0 and V(x) > 0 (< 0) for x ≠ 0. If V(0) = 0 and V(x) ≥ 0 (≤ 0), the function is
said to be positive (negative) semidefinite.
Stability and instability theorems
Consider the autonomous system
)(xfx
=
&
(2.53)
The origin is assumed to be an equilibrium point.

STABILITY BASICS
2-18
Theorem 1: Suppose there exists a positive definite function V(x) which is continuous
together with its first partial derivatives in some neighborhood of the origin and
whose total derivative )(xV
&
along every trajectory of (2.53) is negative
semidefinite, then the origin is stable.
The function V(x) is called a Liapunov function.
Theorem 2: If )(xV
&
is negative definite, then the stability is asymptotic.
An extension of the above theorem is:
Theorem 3: If )(xV
&
is negative semidefinite but not identically zero along any trajectory, then
the origin is asymptotically stable.
Theorem 4: The origin is a globally asymptotically stable equilibrium point if a Liapunov
function V(x) can be found such that (i) V(x) > 0 for all x ≠ 0 with V(0) = 0, (ii)
)(xV
&
< 0 for all x ≠ 0, and (iii) V(x) → ∞ as
∞→x .
Theorem 5: Let V(x) with V(0) = 0 have continuous first partial derivatives in some
neighborhood of the origin. Let )(xV
&
be positive definite and let V(x) be able to
assume positive values arbitrarily near the origin. Then the origin is unstable.
The proof of the above theorems are based on the fact that V(x) being positive definite V = C =
constant represents a one-parameter family of closed surfaces surrounding the origin in the
neighborhood of the origin. For )(xV
&
negative definite any initial state sufficiently close to the
origin must eventually approach the origin
Illustration of positive definite functions and their closedness
Of the three functions
(
)
2
3
2
2
2
13
2
3
2
212
2
3
2
2
2
11
and,, xxxVxxxVxxxV +−=++=++=
the function V
1
is positive definite, the function V
2
is positive semidefinite and the function V
3
is
indefinite.
For the above positive definite function V
1
, V = C surfaces are closed for any C. In general,
however, the surfaces V = C are closed only if C is sufficiently small. An example is provided by
the function
2
2
2
1
2
1
1
x
x
x
V +
+
=
This defines a family of closed curves V = C only if C ≤ 1. Consequently, this can serve as a
Liapunov function only for an investigation of stability in which the disturbances are limited by
the condition
1
1
2
o2
2
o1
2
o1
<+
+
x
x
x
Another example is given by the function
