Типовой расчёт по высшей математике

№11

Даны координаты вершин пирамиды А

1

А

2

А

3

А

4

. Найти: 1) длину ребра А

1

А

2

;

2) угол между рёбрами А

1

А

2

и А

1

А

4

; 3) угол между ребром А

1

А

4

и гранью

А

1

А

2

А

3

; 4) площадь грани А

1

А

2

А

3

; 5) объём пирамиды ; 6) уравнение прямой

А

1

А

2

; 7)уравнение плоскости А

1

А

2

А

3

; 8) уравнение высоты, опущенной из

вершины А

4

на грань А

1

А

2

А

3

.

Сделать схематический чертёж.

А

1

(4;2;5); А

2

(0;7;2); А

3

(0;2;7); А

4

(1;5;0)

Решение

1)Определим длину ребра А

1

А

2.

Длина ребра А

1

А

2

равна длине вектора

21

АА

, координаты и длину которого

определили по формулам

 

;;;

12121221

zzyyxxАА 

(1)

(2)

Подставим в формулы (1), (2) координаты точек А

1

и А

2,

получим:

 

3;5;4

21

АА

;

50)3(5)4(

222

21

АА

Ответ:

50

21

АА

(лин. ед.)

2)Определим угол между рёбрами А

1

А

2

и А

1

А

4

Угол между рёбрами равен углу между векторами

4121

ААиАА

Угол



между векторами определили по формуле

4121

)(

cos

АААА







(3)

Координаты и длину вектора

41

АА

вычислим по формулам (1), (2)

},50;25;41{

41

АА

откуда

}5;3;3{

41

АА

43)5(3)3(

222

41

АА

(лин. ед.)

Так скалярное произведение равно

 

;

zzyyxx

babababа 

(4)

 

42)5()3(35)3(4

4121

 АААА

Подставим полученные значения для

 

41214121

, ААААиАААА 

,

в формулу (3) , получим

9059.0

36.46

42

2150

42

5043

42

cos 







, откуда

 069,25



Ответ: Угол между рёбрами А

1

А

2

и А

1

А

4

 069,25



3) Определим угол между ребром А

1

А

4

и гранью А

1

А

2

А

3.

Угол



между ребром А

1

А

4

и гранью А

1

А

2

А

3

найдём по формуле

Ne





)(

sin



(5)

где

e

направляющий вектор прямой А

1

А

4

;

N

- нормальный вектор плоскости А

1

А

2

А

3

.

В качестве направляющего вектора

e

прямой А

1

А

4

выберем вектор

41

АА

,

2

1

2

12

2

1221

)()()( zzyyxxАА 

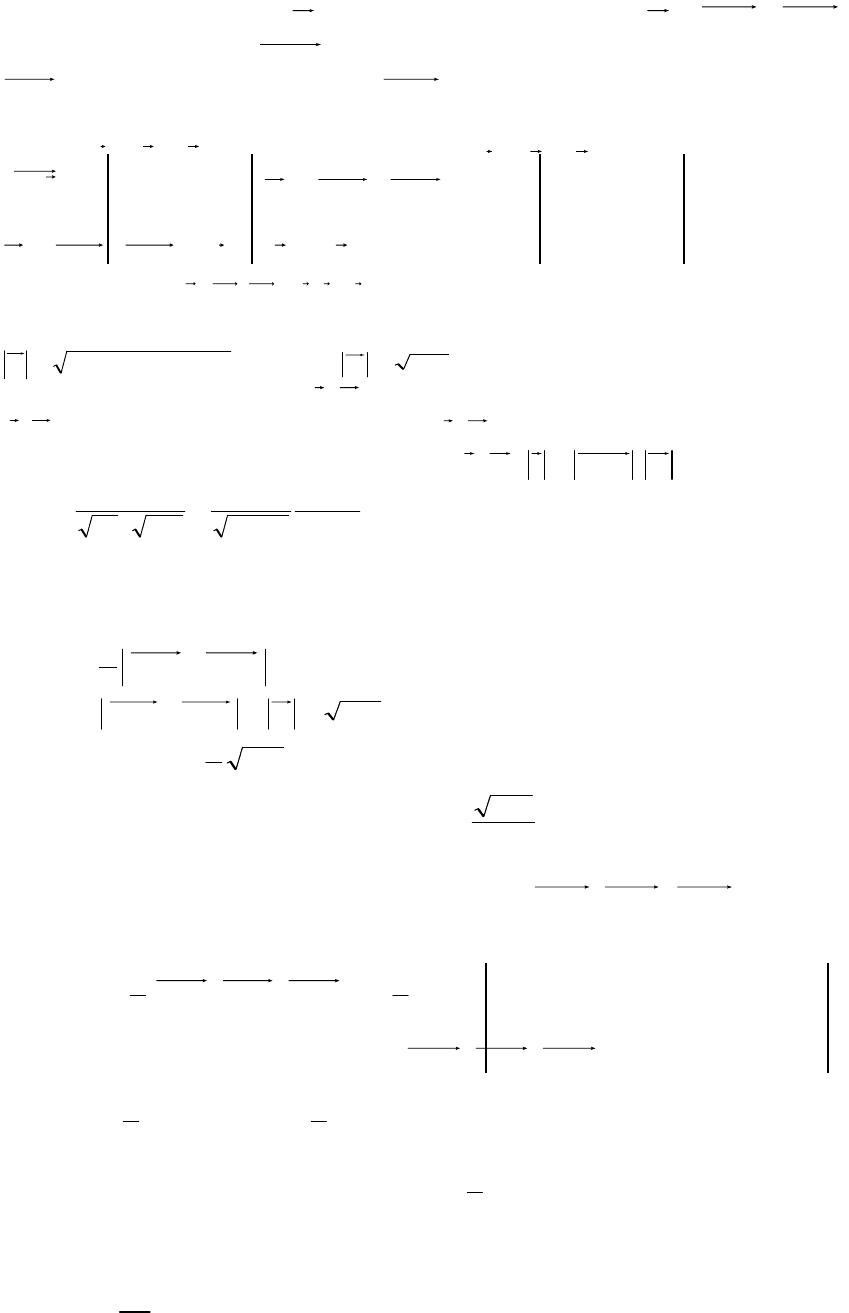
А нормального вектора

N

плоскости А

1

А

2

А

3

- вектор

N

=

 

2131

АААА 

.

Координаты вектора

31

АА

определим по формуле (1)

}57;22;40{

31

АА

, откуда

}2;0;4{

31

АА

Так как векторное произведение

zyx

bbb

aaa

kji

ba 















; то

 

354

204

2131





kji

AAAAN

, откуда

 

kjiAAAAN 20207

2131



Длину вектора

 

}20;20;7{20;20;7{

2131

 kjiAAAAN

Определим по формулам (2)

222

)20(207 N

, откуда

849N

(лин. ед.)

Скалярное произведение

 

Ne 

вычислим по формуле (4)

 

)20()5(20373 Ne

, откуда

 

Ne 

=139

Подставим полученные значения для

 

NAAeNe ,,

41



в формулу (5)

7275.0

06.191

139

36507

139

84943

139

sin 







 67.46



Ответ: угол между ребром А

1

А

4

и гранью А

1

А

2

А

3

 67.46



4) Определим площадь грани А

1

А

2

А

3

.

Площадь грани А

1

А

2

А

3

. найдём с помощью формулы

 

2131

2

1

321

AAAAS

AAA



(7)

Так как

 

849

2131

 NAAAA

(см. предыдущую задачу), то из формулы (7)

следует

849

2

1

321



AAA

S

(кв. ед.)

Ответ: Площадь грани А

1

А

2

А

3

2

849

321



AAA

S

(кв. ед.)

5)Определим объём пирамиды А

1

А

2

А

3

А

4

.

Объём пирамиды, построенной на векторах

413121

ААААиАА 

, как на рёбрах,

определим по формуле

 

141414

131313

121212

413121

;;

6

1

6

1

4321

zzyyxx

AAAAAAV

AAAA





(8)

Подставим координаты векторов

413121

АААААА 

в формулу (8), получим

)85(

6

1

)5(5)4()4(32)3(0)3(

)3(253)3()4()5(04(

6

1

533

204

354

6

1

4321













AAAA

V

Так как определитель равен отрицательному числу, то в данном случае перед

формулой нужно взять знак минус. Следовательно

1,14

6

85

4321



AAAA

V

(куб. ед.)

Ответ: Объём пирамидыА

1

А

2

А

3

А

4

V=14.1 (куб. ед.)

6) Составим уравнение прямой А

1

А

2

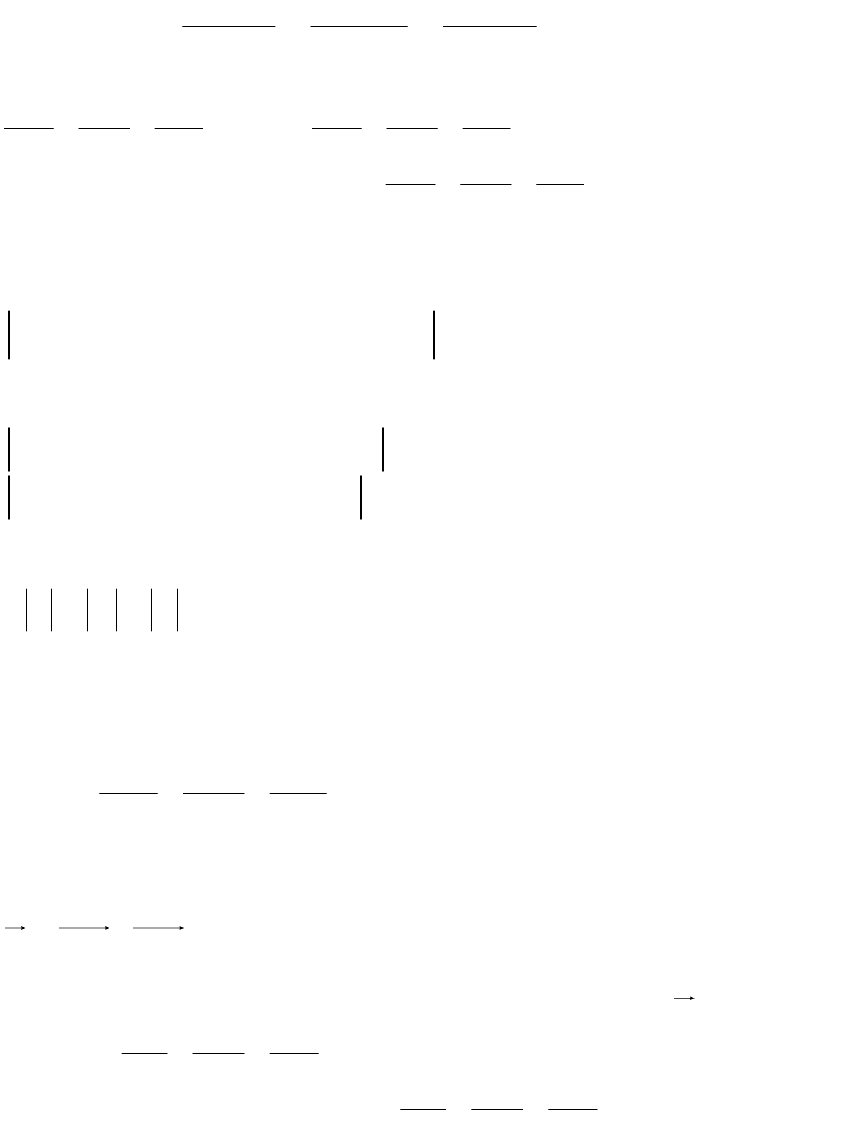
Используем уравнение прямой, проходящей через точки А

1

(x

1

;y

1

;z

1

) и

А

2

(x

2

;y

2

;z

2

):

12

1

12

1

12

1

zz

yy

xx











(9)

Подставим в формулу (9) координаты точек А

1

и А

2

, получим

52

5

27

2

40

4











 zyx

, откуда

3

5

2

4











 zyx

Ответ: Уравнение прямой А

1

А

2

3

5

2

4











 zyx

7)Составим уравнение плоскости А

1

А

2

А

3

.

Используем уравнение плоскости, проходящей через три данные точки

А

1

(x

1

;y

1

;z

1

), А

2

(x

2

;y

2

;z

2

),А

3

(x

3

;y

3

;z

3

)

0

;;

131313

121212

111





zzyyxx

(10)

Уравнение плоскости, проходящей через точки А

1

(4;2;5), А

2

(0;7;2), А

3

(0;2;7)

В соответствии с формулой (10) запишем так

0

572240

52;27;40

5;2;4





 zyx

или

0

204

3;5;4

5;2;4







 zyx

Разлагая последний определитель по элементам первой строки, получим

 

0

04

54

)5(

24

34

)2(

20

35

4 











 zyx

или 10x+20y-20z+180=0

Ответ: Уравнение плоскости А

1

А

2

А

3

10x+20y-20z+180=0

8) Составим уравнение высоты, опущенной из вершины А

4

на грань А

1

А

2

А

3

.

Для составления уравнения высоты А

4

А

5

, проходящей через точку А

4

(x

4

;y

4

;z

4

)

перпендикулярно плоскости А

1

А

2

А

3

, используем каноническое уравнение

прямой

p

zz

n

yy

m

xx

444











(11)

где m, n, p – координаты направляющего вектора этой прямой. В качестве

направляющего вектора высоты А

4

А

5

выберем нормальный вектор

плоскости А

1

А

2

А

3.

 

}20;20;7{

2131

 AAAAN

, который перпендикулярен плоскости А

1

А

2

А

3,

а значит коллинеарен прямой А

4

А

3

. Подставим в уравнение (11) координаты

точки А

4

(1;5;0) и вместо m; n; p – координаты вектора

}20;20;7{ N

,

получим

20

0

20

2

7

1









 zyx

Ответ: Уравнение высоты А

4

А

5

:

20

0

20

2

7

1









 zyx

№21

Уравнение одной из сторон квадрата x+3y-5=0.

Составить уравнение трёх остальных сторон квадрата, если Р(-1; 0)- точка

пересечений его диагоналей. Сделать чертёж.

1)Приведём уравнение прямой x+3y-5=0 к виду y=kx+b

3

5

3

1

 xy

Следовательно прямой перпендикулярна ей будет иметь вид y=3x+b

2

Найдём b

2

, при условии, что данная прямая будет проходить через точку Р(-1;0)

0=-3+ b

2

b

2

=3

y=3x+3

Найдём точку пересечения данной прямой с прямой

3

5

3

1

 xy

8.1

4.

0410

0599

3

1

3

5

33

3

5

3

1

33

























y

x

xx

x

xy

Найдём точку N

1

, образующуюся при пересечении прямой y=3x+3 и стороны

квадрата.

N (x

N

; y

N

)

2

x

= x

k

p

N

x

2

y

=y

k

p

N

y

x

N

=2x

p

-x

k

y

N

=2y

p

-y

k

x

N

= -1.6 y

N

= -1.8 N(-1.6; -1.8)

Проведём через точку N прямую, параллельную x+3y-5=0

3

6,1

8,1 b

3

1

2

3

7

3

6.1

3

4.5

3

b

3

1

2

3

1

 xy

Проведём прямую, параллельную x+3y-5=0, проходящую через P(-1; 0)

k

1

=k

2

3

1

3

1

3

1

3

1

0

3

1

4







xy

b

bxy

Проведём прямую, перпендикулярную прямой

3

1

3

1

 xy

через точку,

отстоящую от точки Р на расстоянии KP.

Для этого составим уравнение окружности, вписанной в данный квадрат

(x-a)

2

+(y-b)

2

=R

2

Для этого найдём расстояние KP.

6,3)8.1()6.0(

)8.1;6.0(

22





KP

Подставим в формулу, где a и b –координаты точки Р, являющейся центром

вписанной окружности

(x+1)

2

+y

2

=3.6

Найдём точку пересечения окружности с прямой

3

1

3

1

 xy





















8.0

8.2

6.0

8.0

y

x

y

x

M (-2; 8; 0.6) L (0,8; -0,6)

Через полученные точки проводим прямые параллельные прямой y=3x+3

1)

93

9

)8.2(36.0

3

5

51











xy

b

bxy

kk

2)

xy

xb

b

bxy

kk

33

4.26.0

3

6

61









Найдём вершины квадрата:

Точка пересечений прямых y=3x+9 и

3

5

3

1

 xy

является

точкой А.

А (-2,2; 2,4)

Точка пересечений прямых y = 3x + 9 и

3

1

2

3

1

 xy

является точкой D

2.14.3

07279

3

1

2

3

1

93



















yx

xx

xy

D (-3,4; -1,2)

Точка пересечений прямых

3

1

2

3

1

 xy

и y = 3x - 3 является точка С

4.22.0

0799

33

3

1

2

3

1



















yx

xx

xy

С (0,2; -2,4)

Точка пересечений прямых y = 3x – 3 и

3

5

3

1

 xy

является точкой B

2.14.1

0599

3

5

3

1

33



















yx

xx

xy

B (1,4; 1,2)

Ответ: y = 3x – 3, y = 3x + 9,

3

1

2

3

1

 xy

, А (-2,2; 2,4), B (1,4; 1,2),

С (0,2; -2,4), D (-3,4; -1,2).

№31

Составить уравнение и построить линию, расстояния каждой точки которой от

начала координат до точки А(5;0) относится как 2:1.

Решение

24.3)1(

24.3

9

10

)1(

9

10

6.3)1(

9

10

6.3)1(

9

1

)1(

)6.3)1(

3

1

()1(

3

1

3

1

6.3)1(

2

22





















x

xx

xy

yx

4.2

2.2

02210

05927

)5(

3

1

93

3

5

3

1

93

























y

x

xx

xy

R

Пусть точка N(x;y) – точка, принадлежащая линии.

Обозначим начало координат точкой О, тогда

1

2



NA

NO

;

NANO 2

;

   

yxNAyxNO  0;5;0;0

2

22

2222

3

10

)

3

20

(

3

100

3)

3

20

(3

3

400

1003)

9

400

3

40

(3

1003)

3

40

(3

01004033

)2510(4

)5(2

























yx

y

x

y

x

xyx

yxxyx

yxyx

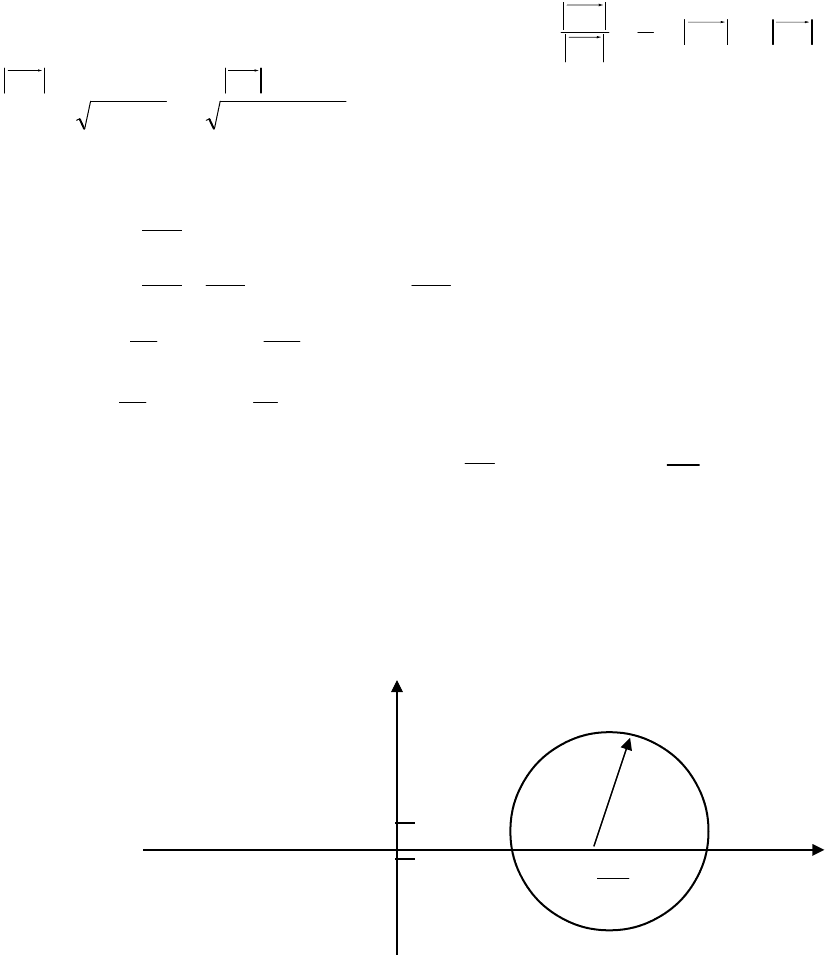
Центр круга находится в точке













0;

3

20

. Радиус =

3

10

Y

1

| | 1 | | | | | | X

-1 -1

3

20

№51

Дана система лінійних рівнянь:













.1132

,132

,523

321

xxx

Доказати її сумісність й рішити двома засобами :

1. Методом Гауса.

2. Методом оберненої матриці.

Розв’язок

1. Знаходимо визначник

 



системи, для того щоб дізнатись про кількість

розв’язків системи, а також доказати її сумісність:

1212362427

312

132

123



Так як

0

, то система має єдиний розв’язок, а тому вона сумісна і може бути

приведена до трикутного вигляду.

Виписуємо з системи розширену матрицю (В) та за допомогою елементарних

перетворень приводимо її до трикутного вигляду.

Елементарні перетворення, що можливі до матриці:

1. Заміна місцями двох рядків (стовбців) матриці.

2. Множення усіх елементів матриці на довільну константу не равну нулю.

3. Додавання якого-небудь рядка (стовбця) відповідно елементів другого

рядка (стовбця) помножено на довільне число.

4. Відкидання усіх нульових рядків (стовбців) матриці.



































































 











































36

13

4

1200

510

011

)2(

10

13

4

220

510

011

)2(10

7

4

220

150

011)1()3(

6

5

4

211

123

011

6

4

5

211

011

123)1(

11

1

5

312

132

123

B

Докажемо, що система сумісна: для того щоб система лінійних рівнянь була

сумісною необхідно і достатньо, щоб ранг розширеної матриці дорівнював

рангу матриці системи.

Ранг – кількість ненульових рядків матриці після приведення її до трикутного

вигляду .

r(A)-ранг матриці; r(B)- ранг розширеної матриці; n – число невідомих.

r(A)=3, r(B)=3, n=3; r(A)= r(B)=n

Ми бачимо, що ранг розширеної матриці дорівнює рангу матриці та числу

невідомих і це значить, що система лін. Рівнянь сумісна і має єдиний розв.

Перейдемо до системи рівнянь :



































3

2

.3612

,135

,4

3

2

1

3

32

21

x

xx

Розв’яжемо систему засобом оберненої матриці:















312

132

123

A

- матриця системи;















11

1

5

B

- матриця вільних членів















3

2

1

x

- матриця невідомих

За формулою Ах=В знаходимо х: А

-1

Ах=А

-1

В

Так як А

-1

А=Е – єдинична матриця

х=А

-1

В

А

-1

- обернена матриця (існує тільки при умові, що матриця А невиражена)

Матриця наз. Невираженою, якщо її визначник не дорівнює нулю.

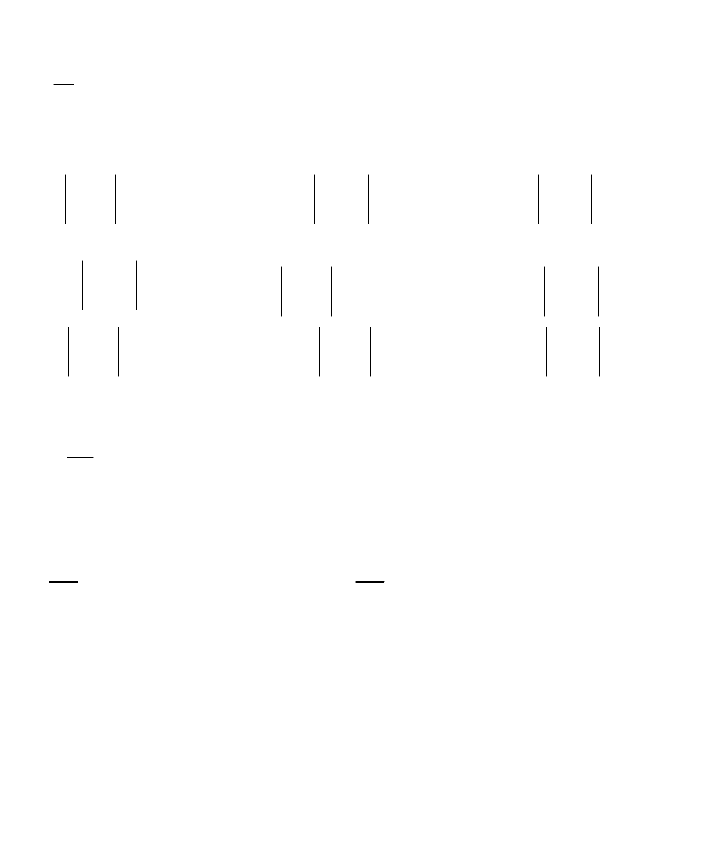
Так як



матриці А

0

то А

-1

– існує

А

-1

=















332313

322212

312111

1

ААА

Знайдемо алгебраїчні додатки матриці А:

8

31

13

11

А

4

32

12

А

4

12

32

13

А

7

32

13

22

А

1

12

23

А

1

13

12

31

А

1

12

13

32

А

5

32

23

33

А

Составимо обернену матрицю А

-1

:





















514

174

158

12

1

А

та за формулую :















































































3

2

3

2

36

24

12

1

11

1

5

514

174

158

12

1

3

2

1

x

Для того, щоб помножити матриці, треба перший рядок множити на перший

стовбець, так ми отримаємо а

11

і потім послідовно множити другий і т.п.

Для того, щоб помножити матрицю, треба, щоб число стовбців множительної

матриці дорівнювало числу рядків множимої матриці. Іначе множення не буде.

Властивості множення:

САВААСВ

СВАСВА

АВВА







)()3

)()()2

)1

Відповідь: x

1

= 2; x

2

= -2; x

3

=3 .

5

31

12

21

А

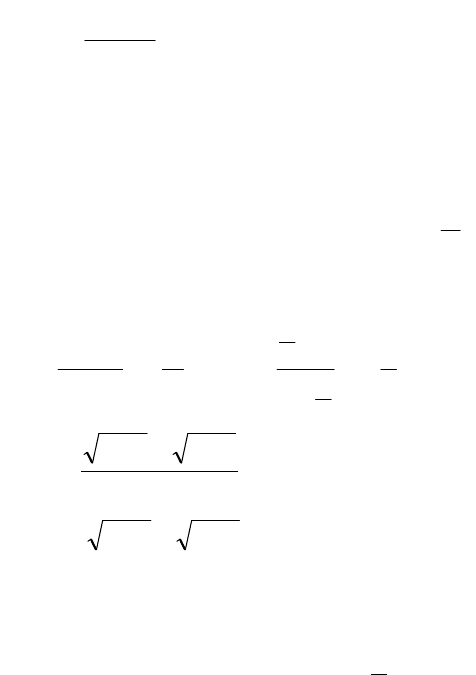
№111

Обчислити границі, не використовуючи правило Лопеаля

а)







23

21

23

21

lim

x

Отже, ми отримали невизначеність















. Вона розкривається діленням

чисельника і знаменника найвищу ступінь многочлена. Поділемо чисельник і

знаменник на х

3

2

3

2

1

23

21

limlim



























x

xx

б)

 

03

011

3

11

lim

0









x

xx

x

xx

x

Ми отримали невизначеність













0

.

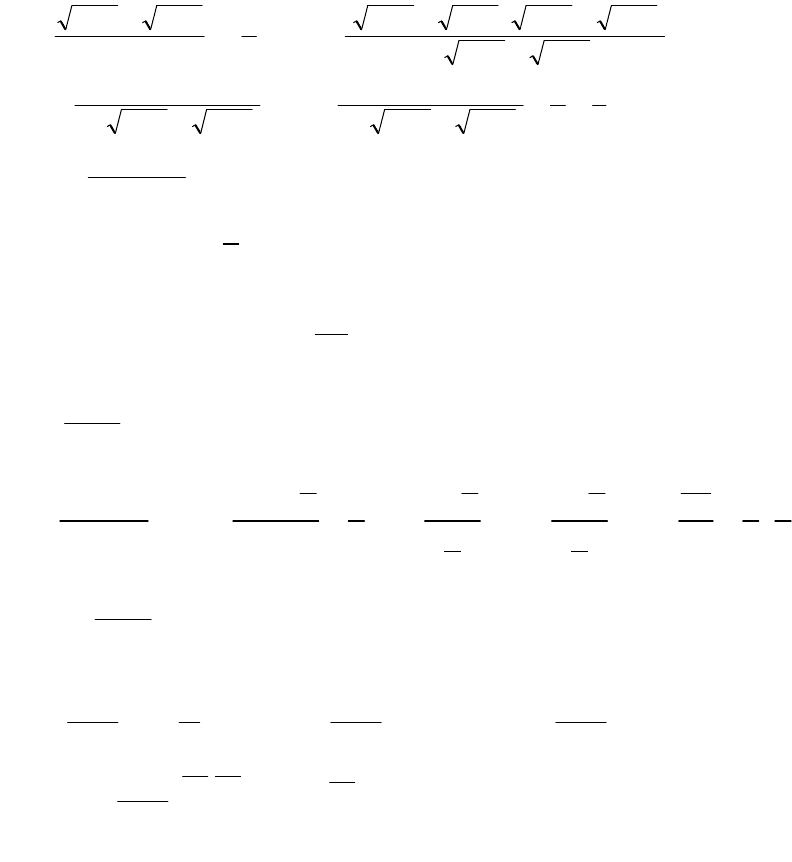
Тепер позбавимось ірраціональності.

  

 

   

3

1

6

2

113

2

113

11

113

1111

0

3

11

limlim

00





































xxx

x

xxx

xx

xxx

xxxx

x

xx

в)

2

0

5

cos1

lim

x





Невизначенність













0

.

2

sin2cos1

x

x

. Будемо зводити до І знаменної границі

1

sin

lim

0





x

1.0

4

1

5

2

4

2

sin

2

sin

5

2

5

2

sin2

5

cos1

2

000

2

0

2

0

limlimlimlimlim







x

xxxxx

г)

x



















2

3

lim

Будемо зводити границю до другої знаменної

5

2

5

2

5

2

lim

2

5

1

2

5

11

2

3

1

2

3

lim

limlimlim

ee

x

xx

x

































































































Типовой расчёт по высшей математике

Подождите немного. Документ загружается.