Гельруд Я.Д. Линейное программирование. Учебно-методический комплекс
Подождите немного. Документ загружается.

выяснить, остается ли оптимальное решение упомянутой выше задачи
допустимым, если ввести дополнительное ограничение вида:
а) x
1
+ x
2
+ x
3
+ x
4
≤ 10;
б) x
1
+ x
2
+ x
3
+ x
4
≤ 6;
в) x
2
+ x
3
≤ 0;
г) x
2
+ x
3
≤ –1;
д) x
1
+ x
2
+ x
3
+ x
4
≥10.
Найдите в каждом случае оптимальные решения исходной и двойственной
задач.
14. Пусть требуется
минимизировать
∑
=
T
t
t
y
1
при ограничениях
у
Т
+ у
1
≥ r
1
у
t-1
+ у
t
≥ r
t
(t = 2, 3,..., Т), (1)
у
t
≥ 0 (t =1, 2,..., Т).
Требуется:
а) записать в явном виде все соотношения (1) при Т = 5, r
1
= 8, r
2
= 7, r
3
= 10,
r
4
= 10 и r
5
= 2;
б) считая данную задачу двойственной, записать все соотношения для
соответствующей исходной задачи;
в) найти (с помощью двойственного симплекс-алгоритма) оптимальное
решение двойственной задачи и определить оптимальное решение
соответствующей исходной задачи (Примечание: для этого потребуется не
более пяти итераций);
г) найти (с помощью симплексного алгоритма) оптимальное решение исходной
задачи и вычислить затем оптимальное решение соответствующей двойственной
задачи (Примечание: для этого потребуется не более пяти итераций);
145
д) найти оптимальные решения исходной и двойственной задач в случае,
когда r
1
= 9 (вместо 8).
15. Решите сформулированные ниже задачи, используя прием,
рассмотренный в разд. 5.7:
а) максимизировать 5x
1
+ 14x
2
+ 24x
3
+ 20x
4
при ограничениях
1x
1
+ 6x
2
+ 12x
3
+ 8x
4
≤ 8,
2x
1
+ 2x
2
+ 12x
3
+ 4x
4
≤ 4,
0≤ x
j
≤1 (j=1, 2, 3, 4);
б) максимизировать 9x
1
+ 1x
2
– 15x
3
– 5x
4
при ограничениях
–3x
1
+ 2x
2
+ 9x
3
+ 1x
4
≤ 7,
6x
1
+ 16x
2
– 12x
3
– 2x
4
≤ 10,
0≤ x
j
≤1 (j = 1, 2, 3, 4).
16. Рассмотрите следующую задачу:
максимизировать
∑
=
∗
+
n
j
jjj
xсс
1
)(
δ
при ограничениях
(i=l, 2, ..., m),
∗
=
+=
∑
ii
n
j
iij
bbxа
δ
1
0≤ x
j
.
а) Пусть удалось найти оптимальное базисное решение для некоторого
фиксированного значения δ (скажем, для δ=δ*). Требуется определить нижний
и верхний пределы, в которых может меняться δ, не нарушая оптимальности
базиса, полученного в случае, когда δ=δ*;
б) полученный результат используйте для анализа модели, рассмотренной в
разд. 3.2, где δ*= 0, с
1
*= –1, c
2
*= 0, с
3
* = 0, с
4
* = 2, b
1
* = 1, b
2
*= –20, b
3
* = 0.
146
17. Анализ модели на чувствительность. Рассмотрим следующую задачу
линейного программирования:
максимизировать
∑
=
n
j
jj
xс
1
при следующих ограничениях:
(i=l, 2, ..., m),
i
n
j
iij
bxа ≤
∑
=1
0≤ x
j
.
Пусть F – оптимальное значение целевой функции. Допустим, что значения
с
j
, а
ij
, b
i
точно не заданы, но известно, что они лежат внутри следующих
интервалов:
с
j
-
≤ с
j
≤ с
+
j
, а
ij
-
≤ а
ij
≤ а
+
ij
, b
i
-
≤ b
i
≤ b
+
i
.
Требуется найти значения F, соответствующие указанным выше
граничным точкам.
18. Двойственный симплекс-алгоритм:
а) пусть каждое из ограничений имеет вид неравенства. Требуется
построить метод нахождения допустимого решения соответствующей
двойственной задачи;
б) пусть некоторые из ограничений представлены в виде равенств.
Требуется разработать метод нахождения допустимого решения соот-
ветствующей двойственной задачи путем введения в рассмотрение
искусственных переменных.
19. Переменные, значения которых ограничены сверху:
а) покажите, каким образом можно модифицировать двойственный
симплекс-алгоритм с тем, чтобы приспособить его к решению" задач,
управляемые переменные в которых ограничены сверху;
б) примените этот метод для решения задачи, представленной
соотношениями (5.7.5) и (5.7.6) разд. 5.7;
в) примените этот метод для решения задач, сформулированных в пунктах
147
а) и б) упражнения 15.
Тема 6
1. Рассмотрите задачу коммивояжера с пятью городами, но допустите, что
коммивояжер должен вернуться в город 1, побывав в двух других городах, а
затем посетить два оставшихся города. Определите число возможных
последовательностей.
2. Определите число возможных последовательностей обработки трех
деталей на одном станке, трех деталей на двух станках, двух деталей на трех
станках, двух деталей на четырех станках. Покажите, как изменится результат,
если детали должны обрабатываться в одном и том же порядке на каждом
станке.
3. Рассмотрите задачу выбора номенклатуры продукции на одном
интервале времени, в которой каждой операции х
j
, j = 1, 2,..., n, соответствуют
затраты К
j
на подготовку производства. Подсчитайте, сколько различных
вариантов подготовки производства существует (предполагая, что равенство
всех х
j
нулю является одной из возможностей).
4. Рассмотрите ограничение х
1
+ х
2
+ х
3
+ … + х
п
= N, где любая величина х
j
должна быть неотрицательным целым. Определите число различных
допустимых решений при следующих условиях:
n = 6, N = 1; n = 7, N = 1; n = 6, N = 2; n = 6, N = 6; n = 7, N = 6; n = 6, N = 6
и ограничение задано в виде неравенства ≤; п = 6, N = 1 и ограничение задано
в виде неравенства ≤; п = 6, N = 2 и ограничение задано в виде неравенства ≤.
5. Рассмотрите задачу распределения капиталовложений, в которой
фигурируют 3 группы проектов. В группе 1 имеется восемь проектов и нужно
выбрать два, в группе 2 — десять проектов и нужно выбрать четыре, в группе
3 — семь проектов и нужно выбрать пять. Определите общее число
возможных комбинаций выбора проектов. Покажите, как изменится это число,
если заданное число проектов, выбираемых в каждой группе, является лишь
верхней оценкой допустимого выбора.
148
6. Фирме нужно составить расписание движения трех автомашин,
обслуживающих восемь магазинов. Каждая машина может останавливаться у
одного или нескольких магазинов, но ни в один магазин не допускается
прибытия более одной машины. Определите число различных расписаний
обслуживания магазинов.
7. Фирма выполняет предупредительный ремонт 4 крупных объектов.
Работу на объекте 1 можно начинать в любую из трех недель, на объекте 2 —
в любую из шести недель, на объекте 3 — в любую из двух недель и на
объекте 4 — в любую из пяти недель. Подсчитайте общее число различных
календарных планов ремонта (т.е. «недель, в которых начинается работа», на
каждом из четырех объектов).
8. Фирма разрабатывает стратегию организации сбыта трех новых видов
продукции в четырех районах. Стратегия строго «последовательна» в том
смысле, что сначала выбирается один район, а затем порядок выпуска на
рынок продукции каждого вида (по одному виду через каждые две недели),
далее выбирается следующий район и порядок выпуска на рынок всех видов
продукции и т. д. Подсчитайте общее число различных стратегий организации
сбыта новой продукции.
9. Фирма планирует строительство шести новых предприятий в
предварительно выбранных пунктах. Строительство всего этого комплекса
рассчитано на пять лет. Допускается возможность строительства всех
предприятий как в течение первого года, так и в течение
пятого года. Более
правдоподобно предположить, что какие-то предприятия будут строиться в
течение каждого года. Определите число возможных вариантов строительства
этих предприятий при этом условии. Фирму интересует также число
предприятий, строящихся ежегодно (в дополнение к числу предприятий,
строившихся в предыдущем году). Определите все возможные варианты
строительства предприятий в рамках пятилетнего интервала времени
(например, шесть в течение первого года и ни одного в последующие годы или
149
шесть в течение пятого года и ни одного в предыдущие и т.д.).
10. Рассмотрите задачу
Максимизировать 3х
1
+ 6х
2
+ х
3
при ограничениях
х
1
+ 2х
2
+ 2х
3
≤ 2
2
/
3
,
х
1
+ 2х
2
+ 3х
3
≤ 2
1
/
2
,
любое х
j
— неотрицательное целое.
а) Каково оптимальное решение, если снять условие целочисленности на
каждую переменную х
j
? Существует ли более одного оптимального решения?
б) Определите путем простого подбора оптимальное целочисленное
решение. Округляется ли ответ, полученный в п. а) до этого решения?
в) Представьте задачу графически в пространстве решений, приняв х
3
= 0
(т.е. начертите ограничения на х
1
и х
2
). Укажите все допустимые
целочисленные решения.
150
К
К
К
О
О
О
Н
Н
Н
Т
Т
Т
Р
Р
Р
О
О
О
Л
Л
Л
Ь
Ь
Ь
Н
Н
Н
Ы
Ы
Ы
Е
Е
Е
З
З
З
А
А
А
Д
Д
Д
А
А
А
Н
Н
Н
И
И
И
Я
Я
Я
1. По данным, приведенным в табл. N, где N – номер варианта, составить
математическую модель задачи линейного программирования (без требования
целочисленности значений переменных).
2. Найти оптимальное решение симплекс-алгоритмом.
3. Определить существенные и несущественные ресурсы и их избытки.
4. Провести полный анализ устойчивости оптимального решения.
5. Составить двойственную задачу линейного программирования.
6. Найти оптимальное решение двойственной задачи.
7. Провести анализ оптимального решения в условиях целочисленности значений
переменных.
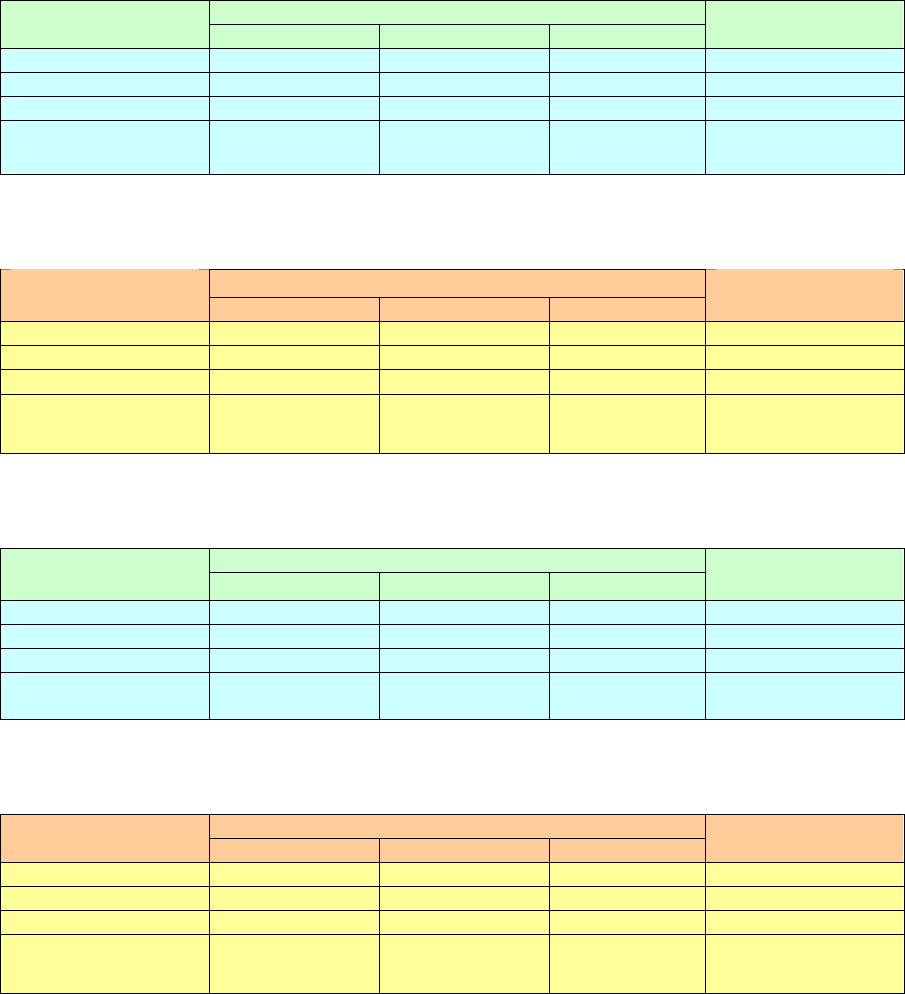
Таблица 1
Нормы на одно изделие Показатель
Ресурс 1 Ресурс 2 Ресурс 3
Прибыль
на одно изделие
Изделие 1
10.0 14.0 3.8 40
Изделие 2
22.0 7.5 14.5 75
Изделие 3
32.0 10.5 8.5 55
Наличие
ресурсов
450 310 360 -
Таблица 2
Нормы на одно изделие
Показатель
Ресурс 1 Ресурс 2 Ресурс 3
Прибыль
на одно изделие
Изделие 1
2.4 8.0 6.2 50
Изделие 2
12.2 5.4 2.2 40
Изделие 3 22.0 7.5 14.5 75
Наличие
ресурсов
500 470 340 -
Таблица 3
Нормы на одно изделие Показатель
Ресурс 1 Ресурс 2 Ресурс 3
Прибыль
на одно изделие
Изделие 1
30 15 12 10
Изделие 2
22.0 7.5 14.5 75
Изделие 3
12 24 30 60
Наличие
ресурсов
400 650 240 -
Таблица 4
Нормы на одно изделие Показатель
Ресурс 1 Ресурс 2 Ресурс 3
Прибыль
на одно изделие
Изделие 1
22.0 7.5 14.5 75
Изделие 2
10 5 21 50
Изделие 3
30 8 14 30
Наличие
ресурсов
250 120 300 -
151

Таблица 5
Нормы на одно изделие Показатель
Ресурс 1 Ресурс 2 Ресурс 3
Прибыль
на одно изделие
Изделие 1
12.2 8.4 4.2 35
Изделие 2
22.0 7.5 14.5 75
Изделие 3
8.2 4.6 12.0 50
Наличие
ресурсов
500 720 300 -
Таблица 6
Нормы на одно изделие Ппоказатель
Ресурс 1 Ресурс 2 Ресурс 3
Прибыль
на одно изделие
Изделие 1
12.6 17.6 24.0 40
Изделие 2
22.0 7.5 14.5 75
Изделие 3
8.2 3.8 12.1 60
Наличие
ресурсов
500 720 310 -
Таблица 7
Нормы на одно изделие Показатель
Ресурс 1 Ресурс 2 Ресурс 3
Прибыль
на одно изделие
Изделие 1
22.0 7.5 14.5 75
Изделие 2
10.0 14.0 9.6 50
Изделие 3
20.0 7.4 12.4 70
Наличие
ресурсов
440 280 320 -
Таблица 8
Нормы на одно изделие Показатель
Ресурс 1 Ресурс 2 Ресурс 3
Прибыль
на одно изделие
Изделие 1
9.2 10.0. 23.0 20
Изделие 2
22.0 7.5 14.5 75
Изделие 3
15.0 5.0 12.0 70
Наличие
ресурсов
400 300 340 -
Таблица 9
Нормы на одно изделие Показатель
Ресурс 1 Ресурс 2 Ресурс 3
Прибыль
на одно изделие
Изделие 1
12.0 8.0 24.0 25
Изделие 2
22.0 7.5 14.5 75
Изделие 3
8.0 4.0 12.0 35
Наличие
ресурсов
500 320 400 -
152
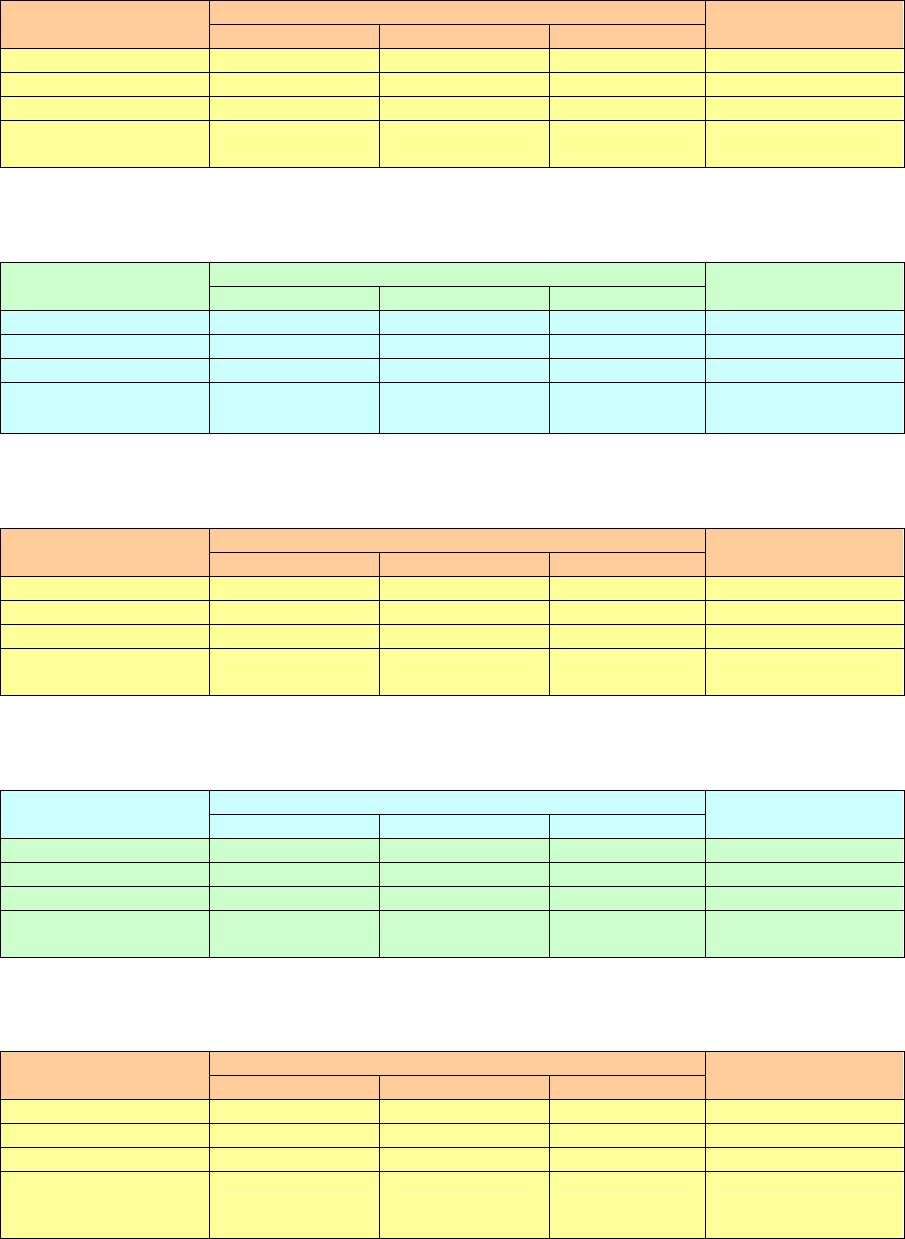
Таблица 10
Нормы на одно изделие Показатель
Ресурс 1 Ресурс 2 Ресурс 3
Прибыль
на одно изделие
Изделие 1
14.0 6.0 12.0 25
Изделие 2
22.0 7.5 14.5 75
Изделие 3
12.6 3.4 15.2 15
Наличие
ресурсов
300 160 200 -
Таблица 11
Нормы на одно изделие Показатель
Ресурс 1 Ресурс 2 Ресурс 3
Прибыль
на одно изделие
Изделие 1
12.2 8.2 4.4 35
Изделие 2
22.0 7.5 14.5 75
Изделие 3
8.4 4.0 12.2 55
Наличие
ресурсов
400 120 260 -
Таблица 12
Нормы на одно изделие Показатель
Ресурс 1 Ресурс 2 Ресурс 3
Прибыль
на одно изделие
Изделие 1
9.0 12.0 13.0 25
Изделие 2
12.0 7.5 14.5 75
Изделие 3
21.0 7.0 14.0 60
Наличие
ресурсов
310 305 340 -
Таблица 13
Нормы на одно изделие Показатель
Ресурс 1 Ресурс 2 Ресурс 3
Прибыль
на одно изделие
Изделие 1
6.5 10.0 12.0 30
Изделие 2
12.0 7.5 14.5 45
Изделие 3
9.0 12.6 10.0 20
Наличие
ресурсов
200 160 300 -
Таблица 14
Нормы на одно изделие Показатель
Ресурс 1 Ресурс 2 Ресурс 3
Прибыль
на одно изделие
Изделие 1
9.2 11.0 4.0 80
Изделие 2
12.0 17.5 14.5 75
Изделие 3
20.0 7.5 12.0 60
Наличие
ресурсов
400 300 350 -
153

Таблица 15
Нормы на одно изделие Показатель
Ресурс 1 Ресурс 2 Ресурс 3
Прибыль
на одно изделие
Изделие 1
12.5 6.8 8.6 40
Изделие 2
22.0 7.5 14.5 75
Изделие 3
8.2 4.4 13.2 50
Наличие
ресурсов
310 120 240 -
Таблица 16
Нормы на одно изделие Показатель
Ресурс 1 Ресурс 2 Ресурс 3
Прибыль
на одно изделие
Изделие 1
12.2 8.4 10.2 25
Изделие 2
22.0 7.5 14.5 45
Изделие 3
8.6 4.2 12.0 35
Наличие
ресурсов
400 200 280 -
Таблица 17
Нормы на одно изделие Показатель
Ресурс 1 Ресурс 2 Ресурс 3
Прибыль
на одно изделие
Изделие 1
12.0 8.2 10.0 30
Изделие 2
22.0 7.5 14.5 35
Изделие 3
8.4 4.4 13.0 55
Наличие
ресурсов
420 260 310 -
Таблица 18
Нормы на одно изделие Показатель
Ресурс 1 Ресурс 2 Ресурс 3
Прибыль
на одно изделие
Изделие 1
11.6 6.4 13.2 35
Изделие 2
22.0 7.5 14.5 55
Изделие 3
6.0 11.4 12.2 50
Наличие
ресурсов
420 280 340 -
Таблица 19
Нормы на одно изделие Показатель
Ресурс 1 Ресурс 2 Ресурс 3
Прибыль
на одно изделие
Изделие 1
12.0 7.4 9.2 40
Изделие 2
22.0 7.5 14.5 50
Изделие 3
6.4 11.6 12.4 60
Наличие
ресурсов
340 280 240 -
154
