Гельруд Я.Д. Линейное программирование. Учебно-методический комплекс

Подождите немного. Документ загружается.

В случае неудовлетворительной оценки за практическое задание по

отдельной теме студент должен выполнить работу над ошибками и

дополнительно решить другие примеры (за каждый неправильно решенный

пример – один дополнительно).

Если контрольная работа не зачтена, то студент должен выполнить

работу над ошибками и затем заново написать другой вариант контрольной

работы. Номер варианта определяется по третьей и четвертой букве фамилии

студента. Так, например, студент Иванов в этом случае должен будет

выполнять повторно вариант 13 контрольного задания.

Тема 1. Построение линейных оптимизационных моделей

1.1. Введение

Линейное программирование, безусловно, относится к числу наиболее

широко распространенных методов исследования операций, используемых

при решении производственных и коммерческих задач. Действительно,

имеются весьма серьезные основания утверждать, что этот метод является

экономически наиболее эффективным.

Качественный анализ. Чтобы разобраться в особенностях данного этапа

анализа, рассмотрим некоторые конкретные «операции», выполняемые каким-

нибудь крупным промышленным предприятием с типовыми

технологическими процессами (к числу предприятий такого рода можно, в

частности, отнести нефтеперерабатывающие заводы, металлургические

комбинаты, деревообрабатывающие комбинаты и т. п.). Рассмотрим,

например, крупную нефтяную компанию. Наиболее важные управляющие

решения в этом случае связаны со следующими процессами:

 геологическая разведка с целью обнаружения нефтяных месторождений;

 добыча сырой нефти (нефтесырья);

 обмен сырой нефти, добываемой фирмой, на нефтесырье других

нефтяных компаний;

 дополнительная закупка сырой нефти;

 доставка нефти на нефтеперегонные заводы;

 крекинг и ректификация с целью получения различных нефтепродуктов

для смешения (промежуточных продуктов);

 получение многочисленных видов готовой продукции в результате

соединения промежуточных нефтепродуктов (в различных комбинациях

и пропорциях);

 доставка (транспортировка) готовой продукции к местам сбыта.

Причем, решение, принимаемое для повышения эффективности одного

процесса, по всей вероятности, может определенным образом затронуть и все

другие процессы, перечисленные выше.

В качестве другого примера рассмотрим фирму, которая, имея в своем

распоряжении лесомассивы (лес на корню), производит заготовку и обработку

древесины, выпускает широкий ассортимент различных изделий из дерева и

продает готовую продукцию в различных географических районах. Как и в

примере с нефтяной компанией, все стратегические решения рассматриваемой

фирмы должны учитывать самое существенное ограничение, определяемое

свойствами материала, используемого в качестве сырья. В данном случае

существенным является то, что из одного бревна можно изготовить лишь

ограниченное количество различных видов пиломатериалов. Чтобы получить

прибыль, фирма должна рационально распределить различные сорта

пиломатериалов по номенклатуре выпускаемой продукции (для каждого вида

готовой продукции требуется определенный сорт пиломатериалов). Таким

образом, ассортимент окончательной продукции должен быть таким, чтобы

лесоматериалы использовались полностью. Однако даже при такой постановке

вопроса остается значительная свобода выбора конкретной номенклатуры

продукции, выпускаемой фирмой.

Несмотря на очевидные упрощения, приведенные примеры являются

хорошей иллюстрацией проблем, с которыми приходится сталкиваться

фирмам при принятии решений, связанных с распределением ресурсов.

Реальные ситуации, как правило, оказываются более сложными. Поэтому

научно-обоснованный экономический анализ последствий принятия того или

иного решения связан с еще большими трудностями. Однако задачи именно

такого рода успешно решались многими крупными фирмами с помощью

линейных оптимизационных моделей, или, как их обычно называют, моделей

линейного программирования.

Потенциальные возможности линейного программирования. Как

будет показано ниже, линейное программирование позволяет резко увеличить

аналитические возможности управляющего фирмы и его аппарата.

Рассматриваемые здесь математические модели дают руководителю

возможность проанализировать такой широкий спектр возможных планов

распределения ресурсов, о каком он не мог ранее и мечтать. Однако важно

отдавать себе отчет в том, что результаты такого анализа вовсе не подменяют

опыт и интуицию руководителя. Скорее, наоборот, эти результаты позволяют

выявить четко определенные и исчерпывающие данные, необходимые

руководителю для эффективного применения своих знаний.

Наряду с этим необходимо научиться формулировать достаточно

сложные задачи в алгебраическом виде, поскольку при практическом

применении линейного программирования для получения численных решений

возникает необходимость обращаться к помощи ЭВМ. Для использования же

стандартных вычислительных программ требуется алгебраическая запись

модели. Таким образом, необходимо умение переводить словесное описание

задачи на язык математических символов.

В двух приведенных ниже примерах рассматриваются задача

оптимального распределения ресурсов на промышленном предприятии,

имеющем возможность использовать различные комбинации технологических

процессов, и задача рационального составления комбикорма. В третьем

примере исследуется задача составления жидких смесей. Этот пример

содержит элементы подхода, рассмотренного в первых двух задачах, и, кроме

того, характеризуется наличием дополнительных ограничений, определяемых

технологией производства.

1.2. Задача распределения ресурсов

На предприятии, выпускающем неоднородную продукцию, руководитель

стремится определить, какими должны быть уровни производства для каждого

продукта в течение некоторого наперед заданного периода. Эти уровни

ограничены технологическими и другими («внутренними» для данного

предприятия) условиями, заданными в виде линейных соотношений (равенств

или неравенств). В рамках этих ограничений руководство данного

предприятия пытается оптимизировать некоторую конкретную целевую

функцию. В рассматриваемом здесь примере целью является получение

максимальной прибыли. В последующих примерах будут фигурировать и

другие цели (например, минимизация затрат).

Представим себе фирму (назовем ее условно «Мультиконвейер»),

имеющую возможность реализовать от одного до четырех различных типов

производственно-технологических процессов и обладающую правом выбора

того или иного варианта. Технологические процессы первого и второго типов

ориентированы на получение продукции А, а технологические процессы

третьего и четвертого типов – на получение продукции В. Расходы, связанные

с каждым из технологических процессов, определяются трудозатратами

(измеряемыми в человеко-неделях), количеством (в единицах веса)

потребляемого в течение недели материала Y и количеством (в ящиках)

потребляемого в течение недели материала Z. Поскольку затраты, связанные с

различными технологическими процессами, не одинаковы, прибыльность

процессов оказывается разной даже в том случае, когда они используются для

получения продукции одного и того же вида. При составлении

производственного плана на неделю диапазон возможностей предпринимателя

ограничен как за счет людских ресурсов, так и за счет потребляемого сырья

(т. е. материалов Y и Z). Производственно-экономические показатели и все

имеющиеся ограничения представлены в табл. 1.1.

Таблица 1.1

Задача фирмы «Мультиконвейер»

На единицу продукции А

На единицу продукции В

Показатель

техноло-

гический

процесс 1

техноло-

гический

процесс 2

техноло-

гический

процесс 3

техноло-

гический

процесс 4

Имеется в

наличии

(всего)

Количество

человеко-недель

≤15

Количество

материала Y (в

килограммах)

≤120

Количество

материала Z (ед.

измерения – ящик)

≤100

Доход с единицы

продукции

(в долларах)

Максими-

зировать

Объем выпускаемой

продукции

Используя данные, приведенные в табл. 1.1, можно было бы сразу

приняться за построение линейной модели. Однако желательно «умерить

пыл». Посмотрим, прежде всего, какие допущения относительно технологии

производства необходимо принять, чтобы обеспечить линейность модели.

Аксиомы линейности. Примем следующие два допущения, играющие

исключительно важную роль при анализе (как в технологическом, так и в

экономическом аспектах) упомянутых выше производственно-

технологических процессов:

1. Делимость. Для каждого производственно-технологического процесса

суммарное количество каждого из потребляемых ресурсов и соответствующая

прибыль строго пропорциональны объему выпускаемой продукции (т. е. в

расчете на единицу времени пропорциональны соответствующей

производственной мощности, или, как говорят, уровню производственной

активности). Другими словами, все показатели производственно-

технологического процесса могут быть увеличены или уменьшены при

сохранении их взаимной пропорциональности. Так, например, если увеличить

вдвое все потребляемые ресурсы, то объем выпускаемой продукции и прибыль

также возрастут вдвое. В частности, чтобы произвести в ходе технологиче-

ского процесса 1 десять единиц продукции (x

= 10), необходимо затратить 10

человеко-недель, 70 кг материала Y и 30 ящиков материала Z; при этом

прибыль составит 40 долл. Условие делимости предполагает также, что все

производственно-экономические показатели могут принимать не только

целочисленные, но и дробные значения. Например, с технологической точки

зрения вполне допустимо положить x

= 2,5 или x

= 10/3.

2. Аддитивность. Если значение каждой из управляемых переменных xj

определено (т. е. указан соответствующий уровень производственной

активности), то полное количество каждого из потребленных ресурсов

равняется сумме одноименных ресурсов, затраченных при реализации всех

применявшихся технологических процессов, а полная прибыль равняется

сумме прибылей, получаемых в результате реализации этих технологических

процессов.

Пример: в соответствии с табл. 1.1 для производства единицы продукции

в ходе технологического процесса 1 и единицы продукции в ходе

технологического процесса 3 требуются 2 человеко-недели, 10 кг материала Y

и 13 ящиков материала Z; доход при этом составляет 13 долл.

Постулирование свойств делимости и аддитивности эквивалентно

утверждению о том, что соответствующая математическая модель может быть

представлена в виде линейных соотношений. В более определенной

интерпретации сформулированные выше аксиомы означают, что

применительно к фиксированному производственно-технологическому

процессу доходы строго пропорциональны затраченным ресурсам, а

непропорциональный эффект (технологического или экономического

характера) оказывается невозможным. В реальных ситуациях

сформулированные выше постулаты, позволяющие использовать линейные

модели, могут оказаться справедливыми лишь приближенно (хотя, возможно,

и с достаточной степенью точности). Во всех приведенных в данной главе

примерах предполагается, что условия обоих постулатов выполняются.

В рассматриваемом примере имеется три линейных неравенства

(ограничение на трудозатраты, ограничение на материал Y и ограничение на

материал Z). Прибыль (подлежащая максимизации) задается линейным

соотношением. Более конкретно задача сводится к следующему:

максимизировать прибыль = максимизировать

(4x

+ 5x

+ 9x

+ 11x

) (1.2.1)

при ограничениях

+ 1x

≤ 15 (человеко-недели),

+ 5x

+ 3x

+ 2x

≤ 120 (материал Y), (1.2.2)

+ 5x

+ 10x

+ 15x

≤ 100 (материал Z).

Отрицательные значения уровней производства (объемов выпускаемой

продукции), как, например, x

= – 4,2, не имеют физического смысла; таким

образом, потребуем, чтобы производство не было «отрицательным». Другими

словами, будем считать, что каждая из управляемых переменных

(j = 1, 2, 3, 4) либо равна нулю, либо принимает положительные значения,

т. е. неотрицательна:

≥ 0. (1.2.3)

(О переменной, которая может принимать также и отрицательные

значения, говорят, что она не ограничена в знаке.)

Задача организационного управления заключается в том, чтобы найти

значения всех неизвестных x

, удовлетворяющие соотношениям (1.2.2) и

(1.2.3) и максимизирующие прибыль (1.2.1). Вообще говоря, такие значения не

обязательно являются единственно возможными. Могут существовать

альтернативные оптимальные решения.

Одновременно с желанием определить оптимальные значения для каждой

неизвестной х у руководителя может возникнуть намерение выяснить, каким

образом отразится на получаемой прибыли увеличение каждого из

потребляемых ресурсов, совершенствование того или иного технологического

процесса, изменение стоимости потребляемого сырья (и, следовательно,

изменение прибыльности производственно-технологических процессов) или

использование в процессе производства какого-либо другого ресурса, не

являющегося дефицитным. При решении многих практических задач методом

линейного программирования подобные вопросы оказываются важнее

определения оптимальных значений каждой из переменных x

. Методы такого

рода анализа на чувствительность излагаются в гл. 4.

1.3. Задача рационального составления комбикорма

Пусть крупная свиноферма (условно назовем ее «Суперрацион») имеет

возможность покупать от одного до четырех различных видов зерна и

приготавливать различные виды смесей (комбикормов). Различные зерновые

культуры содержат разное количество питательных компонентов

(ингредиентов). Допустим, что принимаются к расчет четыре компонента.

(Все данные, относящиеся к рассматриваемой задаче, приведены в табл. 1.2.)

Управляющим свинофермой установлено, что комбикорм для свиней должен

удовлетворять, по крайней мере, некоторым минимальным требованиям с

точки зрения питательности; он стремится определить, какая из всех

возможных смесей является самой дешевой. Допустим, что период.

планирования в данном случае равен двум неделям, т. е. зерно покупается в

количестве, достаточном для прокорма имеющегося поголовья свиней в

течение двух недель.

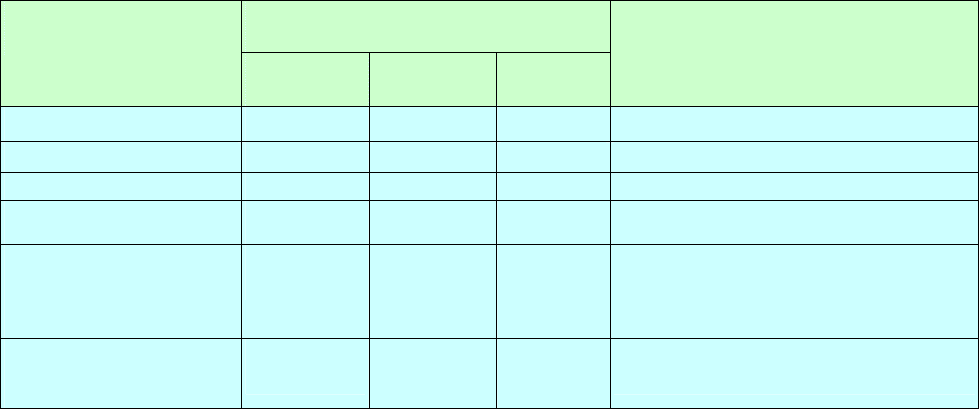
Таблица 1.2

Задача оптимального составления комбикорма

Единица веса

Показатель

зерна 1

зерна 2 зерна 3

Минимальные суммарные

потребности на планируемый

период

Ингредиент А

2,00 3,00 7,00

≥1250

Ингредиент В

1,00 1,00 0

≥250

Инг

едиент С

5,00 3,00 0

≥900

Ингредиент D

0,60 0,25 1,00

≥232,5

Затраты в расчете

на единиц

веса

(цена)

41,00

35,00

96,00

Минимизировать

Количество

(в единицах веса)

Предполагая, что имеют место свойства делимости и аддитивности,

сформулируем рассматриваемую задачу в следующем виде:

минимизировать затраты = минимизировать

(41x

+ 35x

+ 96x

) (1.3.1)

при наличии ограничений

+ 3x

+ 7x

≥ 1250,

+ 1x

≥ 250,

+ 3x

≥ 900, (1.3.2)

0,6x

+ 0,25x

+ 1x

≥ 232,5,

≥ 0 (j = 1, 2, 3).

Интерпретация соотношений (1.3.1) и (1.3.2) представляется читателю.

Следует заметить, что в реальной действительности рассматриваемая

задача, так же, как и задача распределения ресурсов, может содержать

управляемые переменные в количестве, превышающем число ограничений. В

предыдущем примере нулевые значения всех трех переменных (xj = 0)

являются допустимыми в том смысле, что при этом все условия,

определяемые ограничениями, удовлетворяются. В рассматриваемом примере

значения x

= 625, x

= x

= 0 являются допустимыми. Оптимальное же

решение, оказывается, имеет следующий вид: x

= 200, x

= 50, x

= 100. При

этом суммарные затраты минимальны и составляют 19 550 долл.

Управляющий свинофермой помимо значений для каждого из x

возможно, захочет получить некоторую дополнительную информацию,

поскольку рассматриваемая модель может оказаться слишком упрощенным

представлением реальной задачи. Так, например, управляющий может

заинтересоваться, во сколько ему обойдется использование неоптимальных

значений для некоторой конкретной переменной x

; насколько содержание

каждого ингредиента в оптимально составленной кормовой смеси превышает

минимально необходимое содержание этого ингредиента; сколько удалось бы

ему «сэкономить» за счет снижения минимума требований к содержанию

различных ингредиентов в комбикорме; до какого уровня должна снизиться

цена нового кормового продукта (например, четвертого вида зерна), когда

стоит серьезно задуматься над возможностью его использования для

приготовления комбикорма. Все эти вопросы относятся к области анализа на

чувствительность.

1.4. Задача составления жидких смесей

Еще один класс моделей, аналогичных рассмотренным выше, возникает

при решении экономической проблемы, связанной с изготовлением смесей

различных жидкостей (например, нескольких сортов сырой нефти,

доведенных до расплавленного состояния различных металлов и пр.) с целью

получения пользующихся спросом полуфабрикатов или готовой продукции. В

отличие от предыдущих примеров, где приводились конкретные числовые

данные, сформулируем задачу составления жидких смесей в общем виде, т. е.

используя символические обозначения.

Представим себе фирму (назовем ее условно «Алхимик»), торгующую

различного рода химическими продуктами, каждый из которых является

смесью нескольких компонентов. Предположим, что эта фирма планирует

изготовление смесей трех видов. В рамках ограничений технологического

характера и при наличии сырья каждый из продуктов может быть получен

путем использования, по крайней мере, одного из двух возможных

химических компонентов. Обозначим подлежащие определению «уровни

производственной активности» через x

равно числу литров i-го

химического компонента, используемого для получения j-го продукта). Будем

предполагать, что xij ≥ 0. В рассматриваемом ниже примере i = 1, 2, а

= 1, 2, 3.

Первая пара ограничений относится к объемам потребляемых химических

компонентов:

+ x

≤ S

+ x

≤ S

, (1.4.1)

где S

— объем i-го химического компонента, которым располагает фирма в

начале планируемого периода. Первое из ограничений означает, что

суммарное количество химического компонента 1, используемого для

получения продуктов 1, 2 и 3, не может превышать S

, т. е. имеющегося в

наличии объема данного компонента. Второе ограничение в (1.4.1)

интерпретируется аналогичным образом.

Вторая группа ограничений отражает требование, заключающееся в том,

чтобы запланированный выпуск продукции хотя бы в минимальной степени

удовлетворял имеющийся спрос на каждый из химических продуктов, т. е.

+ x

≥ D

+ x

≥ D

, (1.4.2)

+ x

≥ D

где Dj — минимальные потребности покупателей в j-м продукте в течение

планируемого периода. Будем считать, что волюметрические потери в

процессе смешивания данных химических компонентов отсутствуют. Тогда

первое ограничение в (1.4.2) означает, что суммарное количество продукта 1,

получаемого путем смешивания химических компонентов 1 и 2, должно

удовлетворять, по крайней мере, минимальный уровень спроса D

. Два других

ограничения в (1.4.2) интерпретируются аналогичным образом.

Следующее ограничение связано с технологическими особенностями,

которые необходимо принимать во внимание при приготовлении смеси

первого типа (т. е. продукта 1). Допустим, что в каждом из используемых

химических компонентов содержится некоторый определяющий ингредиент.

Пусть, например, количество этого ингредиента в одном литре i-го

химического компонента равняется а

. Ограничение отражает требование,

чтобы при изготовлении продукта 1 данный ингредиент содержался в

пропорции, определяемой соотношением

2111

212111

хх

хаха

≥

(1.4.3)

Ограничение аналогичного характера возможно и при получении

продукта 2. Пусть оно имеет вид

2212

222121

хх

хbхb

≥

(1.4.4)

т. е. имеет место ограничение сверху. Нетрудно убедиться, что. с помощью

ряда алгебраических преобразований соотношения (1.4.3) и (1.4.4) можно

привести к нормальному линейному виду

– r

) x

+ (a

– r

) x

≥ 0,

– r2) x

+ (b

– r

) x

≤ 0. (1.4.5)

Наконец, может иметь место простое ограничение, определяемое некоторыми

минимально допустимыми значениями отношения между объемами двух

химических компонентов в процессе получения продукта 3:

≥

или x

– r

≥ 0. (1.4.6)

Обозначив через р

доход с единицы продукции х

, запишем целевую

функцию в виде

+ р

, (1.4.7)

которую необходимо максимизировать.