Gibilisco S. Teach Yourself Electricity and Electronics
Подождите немного. Документ загружается.

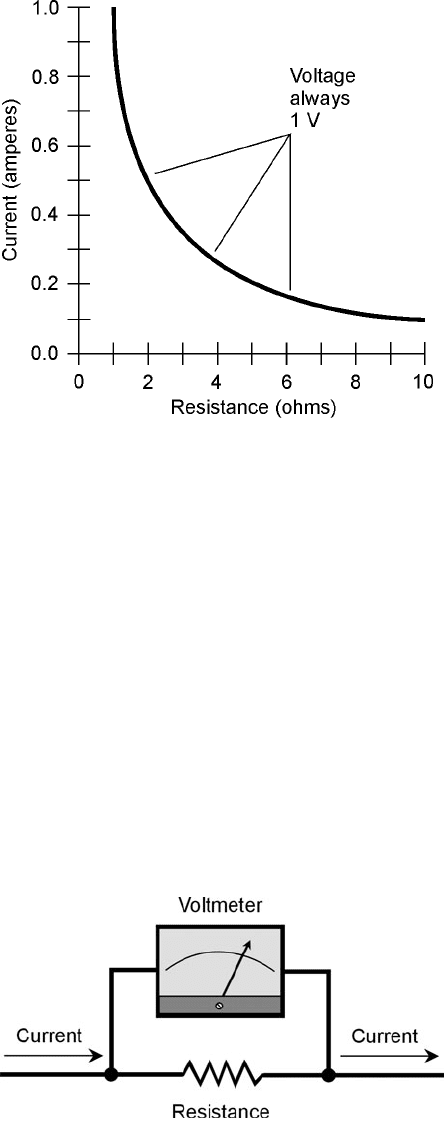
When 1 V is placed across 1 Ω of resistance, assuming that the power supply can deliver an un-
limited number of charge carriers, there is a current of 1 A. If the resistance is doubled to 2 Ω, the
current decreases to 0.5 A. If the resistance is cut by a factor of 5 to 0.2 Ω, the current increases by
the same factor, to 5 A. The current flow, for a constant voltage, is said to be inversely proportional
to the resistance. Figure 2-3 is a graph that shows various currents, through various resistances, given
a constant voltage of 1 V across the whole resistance.
Resistance has another property. If there is a current flowing through a resistive material, there
is always a potential difference across the resistive component (called a resistor). This is shown in
Fig. 2-4. In general, this voltage is directly proportional to the current through the resistor. This be-
havior of resistors is useful in the design of electronic circuits, as you will learn later in this book.
Electrical circuits always have some resistance. There is no such thing as a perfect conductor.
When some metals are chilled to temperatures near absolute zero, they lose practically all of their re-
sistance, but they never become absolutely perfect, resistance-free conductors. This phenomenon,
about which you might have heard, is called superconductivity.
Resistance and the Ohm 21
2-4 Whenever current passes
through a component
having resistance, a
voltage exists across that
component.
2-3 Current as a function of
resistance through an
electric device for a
constant voltage of 1 V.
Just as there is no such thing as a perfectly resistance-free substance, there isn’t a truly infinite
resistance, either. Even air conducts to some extent, although the effect is usually so small that it can
be ignored. In some electronic applications, materials are selected on the basis of how “nearly infi-
nite” their resistance is.
In electronics, the resistance of a component often varies, depending on the conditions under
which it is operated. A transistor, for example, might have high resistance some of the time, and low
resistance at other times. High/low resistance variations can be made to take place thousands, mil-
lions, or billions of times each second. In this way, oscillators, amplifiers, and digital devices func-
tion in radio receivers and transmitters, telephone networks, digital computers, and satellite links
(to name just a few applications).
Conductance and the Siemens
Electricians and electrical engineers sometimes talk about the conductance of a material, rather than
about its resistance. The standard unit of conductance is the siemens, abbreviated S. When a com-
ponent has a conductance of 1 S, its resistance is 1 Ω. If the resistance is doubled, the conductance
is cut in half, and vice versa. Therefore, conductance is the reciprocal of resistance.
If you know the resistance of a component or circuit in ohms, you can get the conductance in
siemens: divide 1 by the resistance. If you know the conductance in siemens, you can get the resist-
ance: divide 1 by the conductance. Resistance, as a variable quantity, is denoted by an italicized, up-
percase letter R. Conductance, as a variable quantity, is denoted as an italicized, uppercase letter G. If
we express R in ohms and G in siemens, then the following two equations describe their relationship:
G = 1/R
R = 1/G
Units of conductance much smaller than the siemens are often used. A resistance of 1 kΩ is
equal to 1 millisiemens (1 mS). If the resistance is 1 MΩ, the conductance is one microsiemens (1 µS).
You’ll sometimes hear about kilosiemens (kS) or megasiemens (MS), representing resistances of 0.001
Ω and 0.000001 Ω (a thousandth of an ohm and a millionth of an ohm, respectively). Short lengths
of heavy wire have conductance values in the range of kilosiemens. Heavy metal rods can have con-
ductances in the megasiemens range.
Suppose a component has a resistance of 50 Ω. Then its conductance, in siemens, is 1/50 S,
which is equal to 0.02 S. We can call this 20 mS. Or imagine a piece of wire with a conductance
of 20 S. Its resistance is 1/20 Ω, which is equal to 0.05 Ω. You will not often hear the term mil-
liohm. But you could say that this wire has a resistance of 50 mΩ, and you would be technically
right.
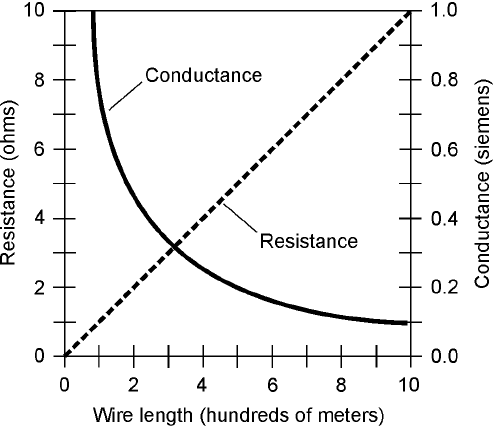
Determining conductivity is tricky. If wire has a resistivity of 10 Ω/km, you can’t say that it has
a conductivity of 1/10, or 0.1, S/km. It is true that a kilometer of such wire has a conductance of
0.1 S, but 2 km of the wire has a resistance of 20 Ω (because there is twice as much wire). That is
not twice the conductance, but half. If you say that the conductivity of the wire is 0.1 S/km, then
you might be tempted to say that 2 km of the wire has 0.2 S of conductance. That would be a mis-
take! Conductance decreases with increasing wire length.
Figure 2-5 illustrates the resistance and conductance values for various lengths of wire having a
resistivity of 10 Ω/km.
22 Electrical Units
Power and the Watt
Whenever current flows through a resistance, heat results. The heat can be measured in watts (sym-
bolized W) and represents electrical power. (As a variable quantity in equations, power is denoted by
the uppercase italic letter P. ) Power can be manifested in many forms, such as mechanical motion,
radio waves, visible light, or noise. But heat is always present, in addition to any other form of
power, in an electrical or electronic device. This is because no equipment is 100 percent efficient.
Some power always goes to waste, and this waste is almost all in the form of heat.
Look again at Fig. 2-4. There is a certain voltage across the resistor, not specifically indicated.
There’s also a current flowing through the resistance, and it is not quantified in the diagram, either.
Suppose we call the voltage E and the current I, in volts (V) and amperes (A), respectively. Then the
power in watts dissipated by the resistance, call it P, is the product of the voltage in volts and the
current in amperes:
P = EI
If the voltage E across the resistance is caused by two flashlight cells in series, giving 3 V, and if
the current I through the resistance (a light bulb, perhaps) is 0.1 A, then E = 3 V and I = 0.1 A, and
we can calculate the power P in watts as follows:
P = EI = 3 × 0.1 = 0.3 W
Suppose the voltage is 117 V, and the current is 855 mA. To calculate the power, we must con-
vert the current into amperes: 855 mA = 855/1000 A = 0.855 A. Then:
P = EI = 117 × 0.855 = 100 W
Power and the Watt 23
2-5 Resistance and
conductance for various
lengths of wire having a
resistivity of 10 ohms
per kilometer.
You will often hear about milliwatts (mW), microwatts (µW), kilowatts (kW), and megawatts
(MW). By now, you should be able to tell from the prefixes what these units represent. Otherwise,
you can refer to Table 2-2. This table lists the most commonly used prefix multipliers in electricity
and electronics.
Sometimes you need to use the power equation to find currents or voltages. Then you should
use I = P/E to find current, or E = P/I to find voltage. Always remember to convert, if necessary, to
the standard units of volts, amperes, and watts before performing the calculations.
A Word about Notation
Have you noticed some strange things about the notation yet? If you’re observant, you have! Why,
you might ask, are italics sometimes used, and sometimes not used? Something should be said early
in this course about notation, because it can get confusing with all the different symbols and abbre-
viations. Sometimes, symbols and abbreviations appear in italics, and sometimes they do not. You’ll
see subscripts often, and sometimes even they are italicized! Here are some rules that apply to nota-
tion in electricity and electronics:
• Symbols for specific units, such as volts, amperes, and ohms, are not italicized.
• Symbols for objects or components, such as resistors, batteries, and meters, are not italicized.
• Quantifying prefixes, such as “kilo-” or “micro-,” are not italicized.
• Labeled points in drawings might or might not be italicized; it doesn’t matter as long as a di-
agram is consistent with itself.
• Symbols for mathematical constants and variables, such as time, are italicized.
• Symbols for electrical quantities, such as voltage, current, resistance, and power, are itali-
cized.
• Symbols and abbreviations for modifiers might or might not be italicized; it doesn’t matter
as long as a document is consistent with itself.
• Numeric subscripts are not italicized.
• For nonnumeric subscripts, the same rules apply as for general symbols.
Some examples are R (not italicized) for resistor, R (italicized) for resistance, P (italicized) for power,
W (not italicized) for watts, V (not italicized) for volts, E or V (italicized) for voltage, A (not itali-
cized) for amperes, I (italicized) for current, f (italicized) for frequency, and t (italicized) for time.
24 Electrical Units
Table 2-2. Prefix multipliers from 0.000000000001
(trillionths, or units of 10
−12
) to 1,000,000,000,000
(trillions, or units of 10
12
).
Prefix Symbol Multiplier
pico- p 0.000000000001 (or 10
−12
)
nano- n 0.000000001 (or 10
−9
)
micro- µ 0.000001 (or 10
−6
)
milli- m 0.001 (or 10
−3
)
kilo- k 1000 (or 10
3
)
mega- M 1,000,000 (or 10
6
)
giga- G 1,000,000,000 (or 10
9
)
tera- T 1,000,000,000,000 (or 10
12
)
Once in a while you will see the same symbol italicized in one place and not in another—in the
same circuit diagram or discussion! We might, for example, talk about “resistor number 3” (symbol-
ized R
3
), and then later in the same paragraph talk about its value as “resistance number 3” (Sym-
bolized R
3
). Still later we might talk about “the nth resistor in a series connection” (R
n
) and then “the
nth resistance in a series combination of resistances” (R
n
).
These differences in notation, while subtle (and, some people will say, picayune) are followed
in this book, and they are pretty much agreed upon by convention. They are important because they
tell the reader exactly what a symbol stands for in a diagram, discussion, or mathematical equation.
“Resistor” and “resistance” are vastly different things—as different from each other as a garden hose
(the object) and the extent to which it impedes the flow of water (the phenomenon). With this in
mind, let us proceed!
Energy and the Watt-Hour
Have you heard the terms “power” and “energy” used interchangeably, as if they mean the same
thing? They don’t! Energy is power dissipated over a length of time. Power is the rate at which energy
is expended. Physicists measure energy in units called joules. One joule (1 J) is the equivalent of a
watt-second, which is the equivalent of 1 watt of power dissipated for 1 second of time (1 W ⭈ s or
Ws). In electricity, you’ll more often encounter the watt-hour (symbolized W ⭈ h or Wh) or the
kilowatt-hour (symbolized kW ⭈ h or kWh). As their names imply, a watt-hour is the equivalent of
1 W dissipated for 1 h, and 1 kWh is the equivalent of 1 kW of power dissipated for 1 h.
A watt-hour of energy can be dissipated in an infinite number of different ways. A 60-W bulb
consumes 60 Wh in 1 h, the equivalent of a watt-hour per minute (1 Wh/min). A 100-W bulb con-
sumes 1 Wh in 1/100 h, or 36 s. Besides these differences, the rate of power dissipation in real-life
circuits often changes with time. This can make the determination of consumed energy compli-
cated, indeed.
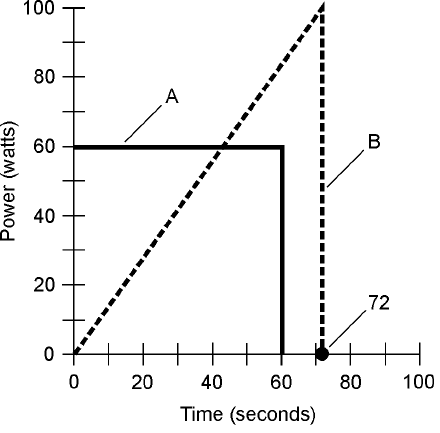
Figure 2-6 illustrates two hypothetical devices that consume 1 Wh of energy. Device A uses its
power at a constant rate of 60 W, so it consumes 1 Wh in 1 min. The power consumption rate of
Energy and the Watt-Hour 25
2-6 Two devices that burn 1
Wh of energy. Device A
dissipates a constant
amount of power.
Device B dissipates a
variable amount of
power.
device B varies, starting at zero and ending up at quite a lot more than 60 W. How do you know
that this second device really consumes 1 Wh of energy? You must determine the area under the
curve in the graph. In this case, figuring out this area is easy, because the enclosed object is a trian-
gle. The area of a triangle is equal to half the product of the base length and the height. Device B is
powered up for 72 s, or 1.2 min; this is 1.2/60 = 0.02 h. Then the area under the curve is 1/2 ×
100 × 0.02 = 1 Wh.
When calculating energy values, you must always remember the units you’re using. In this case
the unit is the watt-hour, so you must multiply watts by hours. If you multiply watts by minutes, or
watts by seconds, you’ll get the wrong kind of units in your answer.
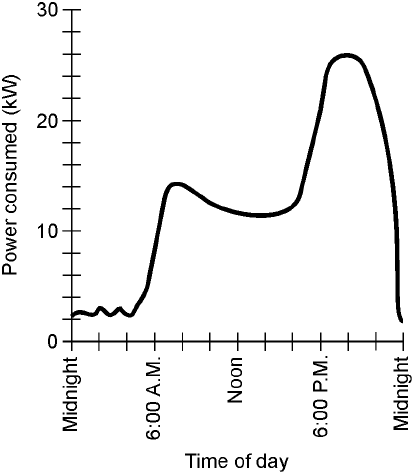
Often, the curves in graphs like these are complicated. Consider the graph of power consump-
tion in your home, versus time, for a day. It might look like the curve in Fig. 2-7. Finding the area
under this curve is not easy. But there is another way to determine the total energy burned by your
household over a period of time. That is by means of a meter that measures electrical energy in kilo-
watt-hours. Every month, without fail, the power company sends its representative to read your
electric meter. This person takes down the number of kilowatt-hours displayed, subtracts the num-
ber from the reading taken the previous month, and a few days later you get a bill. This meter au-
tomatically keeps track of total consumed energy, without anybody having to go through high-level
mathematical calculations to find the areas under irregular curves such as the graph of Fig. 2-7.
Other Energy Units
The joule, while standard among scientists, is not the only energy unit in existence! Another unit is
the erg, equivalent to one ten-millionth (0.0000001) of a joule. The erg is used in lab experiments
involving small amounts of expended energy.
26 Electrical Units
2-7 A graph showing the
amount of power
consumed by a
hypothetical household,
as a function of the time
of day.
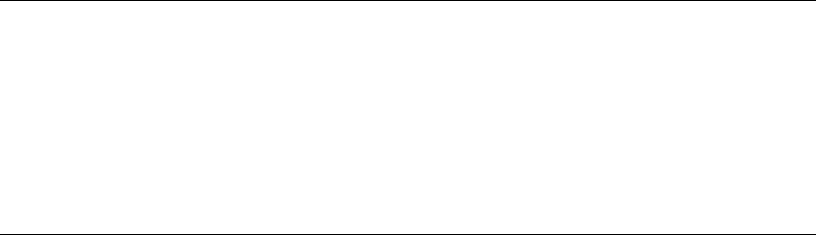
Most folks have heard of the British thermal unit (Btu), equivalent to 1055 joules. This is the
energy unit commonly used to define the cooling or heating capacity of air-conditioning equip-
ment. To cool your room from 85 to 78°F needs a certain amount of energy, perhaps best specified
in Btu. If you are getting an air conditioner or furnace installed in your home, an expert will come
look at your situation, and determine the size of air-conditioning/heating unit that best suits your
needs. That person will likely tell you how powerful the unit should be in terms of its ability to heat
or cool in Btu per hour (Btu/h).
Physicists also use, in addition to the joule, a unit of energy called the electron volt (eV). This is
a tiny unit of energy, equal to just 0.00000000000000000016 joule (there are 18 zeroes after the
decimal point and before the 1). The physicists write 1.6 × 10
−19
to represent this. It is the energy
gained by a single electron in an electric field of 1 V. Machines called particle accelerators (or atom
smashers) are rated by millions of electron volts (MeV), billions of electron volts (GeV), or trillions
of electron volts (TeV) of energy capacity.
Another energy unit, employed to denote work, is the foot-pound (ft-lb). This is the work
needed to raise a weight of one pound by a distance of one foot, not including any friction. It’s equal
to 1.356 joules.
All of these units, and conversion factors, are given in Table 2-3. Kilowatt-hours and watt-hours
are also included in this table. In electricity and electronics, you need to be concerned only with the
watt-hour and the kilowatt-hour for most purposes.
Alternating Current and the Hertz
This chapter, and this whole first section, is mostly concerned with direct current (dc). That’s elec-
tric current that always flows in the same direction and that does not change in intensity (at least
not too rapidly) with time. But household utility current is not of this kind. It reverses direction pe-
riodically, exactly once every 1/120 second. It goes through a complete cycle every 1/60 second.
Every repetition is identical to every other. This is alternating current (ac).
Figure 2-8 shows the characteristic wave of ac, as a graph of voltage versus time. Notice that the
maximum positive and negative voltages are not 117 V, as you’ve heard about household electricity,
but close to 165 V. There is a reason for this difference. The effective voltage for an ac wave is never
the same as the instantaneous maximum, or peak, voltage. In fact, for the common waveform shown
in Fig. 2-8, the effective value is 0.707 times the peak value. Conversely, the peak value is 1.414
times the effective value.
Alternating Current and the Hertz 27
Table 2-3. Conversion factors between joules and various other energy units.
To convert energy To convert energy
in this unit to energy in in joules to energy in
Unit joules, multiply by this unit, multiply by
British thermal units (Btu) 1055 0.000948
Electron volts (eV) 1.6 × 10
−19
6.2 × 10
18
Ergs 0.0000001 (or 10
−7
) 10,000,000 (or 10
7
)
Foot-pounds (ft-lb) 1.356 0.738
Watt-hours (Wh) 3600 0.000278
Kilowatt-hours (kWh) 3,600,000 (or 3.6 × 10
6
) 0.000000278 (or 2.78 × 10
−7
)
Because the whole cycle repeats itself every 1/60 second, the frequency of the utility ac wave is
said to be 60 hertz, abbreviated 60 Hz. The German word hertz literally translates to “cycles per sec-
ond.” In the United States, this is the standard frequency for ac. In some places it is 50 Hz.
In wireless communications, higher frequencies are common, and you’ll hear about kilohertz
(kHz), megahertz (MHz), and gigahertz (GHz). The relationships among these units are as follows:
1 kHz = 1000 Hz
1 MHz = 1000 kHz = 1,000,000 Hz
1 GHz = 1000 MHz = 1,000,000 kHz = 1,000,000,000 Hz
Usually, but not always, the waveshapes are of the type shown in Fig. 2-8. This waveform is known
as a sine wave or a sinusoidal waveform.
Rectification and Pulsating Direct Current
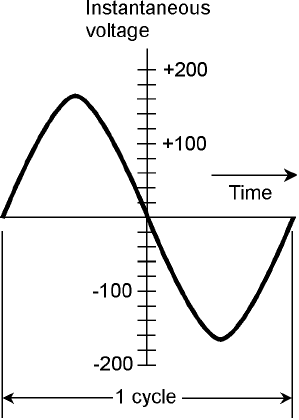
Batteries and other sources of direct current (dc) produce constant voltage. This can be represented
by a straight, horizontal line on a graph of voltage versus time (Fig. 2-9). For pure dc, the peak and
effective values are identical. But sometimes the value of dc voltage fluctuates rapidly with time.
This happens, for example, if the waveform in Fig. 2-8 is passed through a rectifier circuit.
Rectification is a process in which ac is changed to dc. The most common method of doing this
uses a device called the diode. Right now, you need not be concerned with how the rectifier circuit
is put together. The point is that part of the ac wave is either cut off, or turned around upside down,
so the output is pulsating dc. Figure 2-10 illustrates two different waveforms of pulsating dc. In the
waveform at A, the negative (bottom) part has been cut off. At B, the negative portion of the wave
has been inverted and made positive. The situation at A is known as half-wave rectification, because
it involves only half the waveform. At B, the ac has been subjected to full-wave rectification, because
28 Electrical Units
2-8 One cycle of utility
alternating current (ac).
The instantaneous
voltage is the voltage at
any particular instant in
time. The peak voltages
are approximately plus
and minus 165 V.
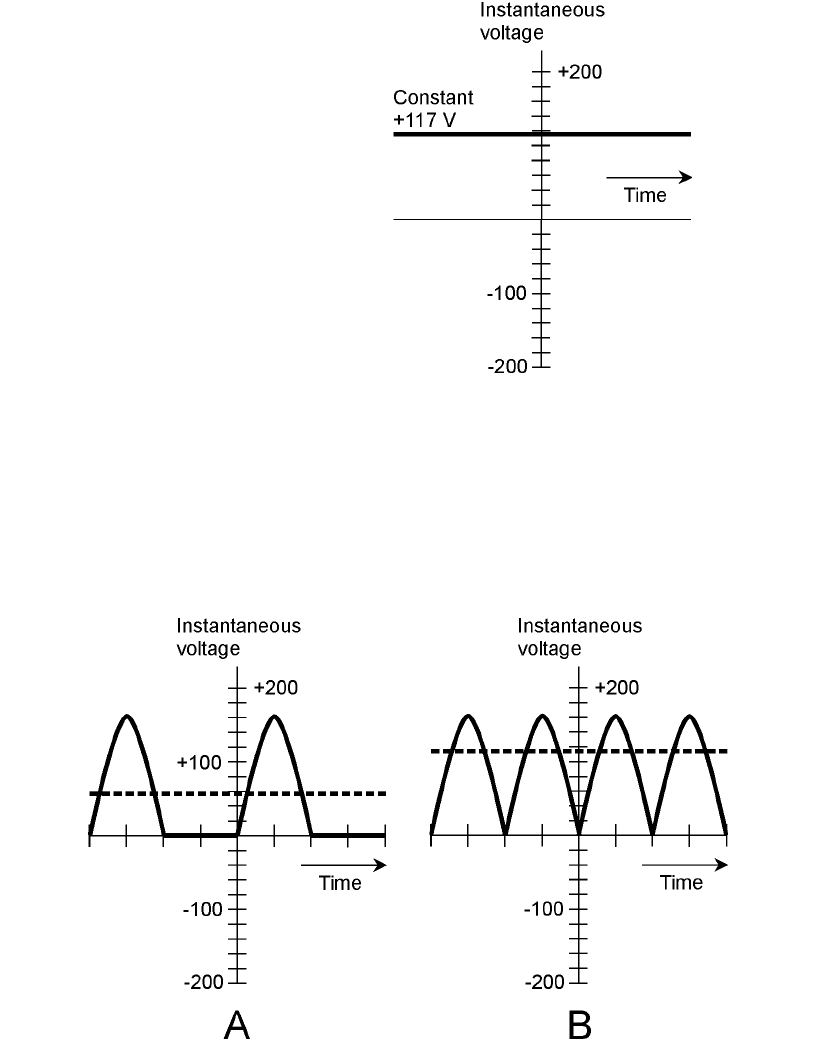
all of the original current still flows, even though the alternating nature has been changed so that the
current never reverses.
The effective value, compared with the peak value, for pulsating dc depends on whether half-
wave or full-wave rectification is applied to an ac wave. In Fig. 2-10A and B, effective voltage is
shown as dashed lines, and the instantaneous voltage is shown as solid curves. The instantaneous volt-
age changes all the time, from instant to instant. (That’s how it gets this name!) The peak voltage is
Rectification and Alternating Current 29
2-10 At A, half-wave rectification of common utility ac. At B, full-wave
rectification of common utility ac. Effective voltages are shown by the
dashed lines.
2-9 A representation of pure
direct current (dc).
the maximum instantaneous voltage. Instantaneous voltage is never any greater than the peak volt-
age for any wave.
In Fig. 2-10B, the effective voltage is 0.707 times the peak voltage, just as is the case with ordi-
nary ac. The direction of current flow, for many kinds of devices, doesn’t make any difference. But
in Fig. 2-10A, half of the wave has been lost. This cuts the effective value in half, so that it’s only
0.354 times the peak value.
In household ac that appears in wall outlets for conventional appliances in the United States,
the peak voltage is about 165 V; the effective value is 117 V. If full-wave rectification is used, the ef-
fective value is still 117 V. If half-wave rectification is used, the effective voltage is about 58.5 V.
Safety Considerations in Electrical Work
For our purposes, one rule applies concerning safety around electrical apparatus:
If you have any doubt about whether or not something is safe, leave it alone. Let a professional
electrician work on it.
Household voltage, normally about 117 V (but sometimes twice that for large appliances such
as electric ranges and laundry machines), is more than sufficient to kill you if it appears across your
chest cavity. Certain devices, such as automotive spark coils, can produce lethal currents even from
the low voltage (12 to 14 V) in a car battery.
Consult the American Red Cross or your electrician concerning what kinds of circuits, proce-
dures, and devices are safe and which aren’t.
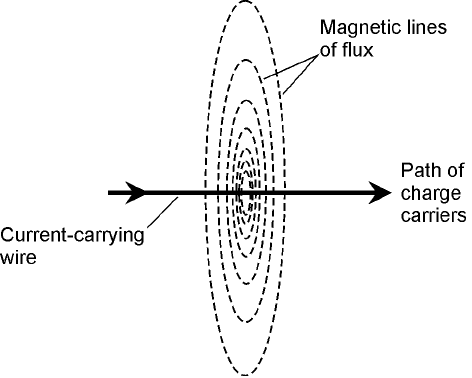
Magnetism
Electric currents and magnetic fields are closely related. Whenever an electric current flows—that is,
when charge carriers move—a magnetic field accompanies the current. In a straight wire that car-
ries electrical current, magnetic lines of flux surround the wire in circles, with the wire at the center,
as shown in Fig. 2-11. (The lines of flux aren’t physical objects; this is just a convenient way to rep-
30 Electrical Units
2-11 Magnetic flux lines
around a straight,
current-carrying wire.
The arrows indicate
current flow.
