Graziani F. (editor) Computational Methods in Transport
Подождите немного. Документ загружается.

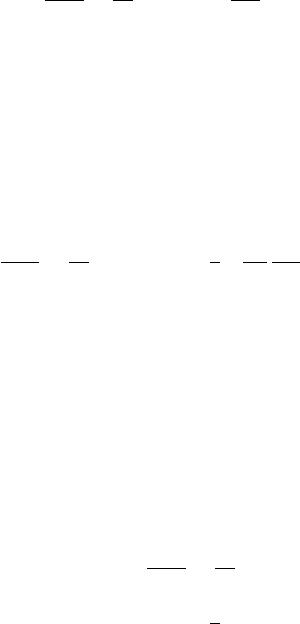
48 A. Mezzacappa et al.
the O(v/c) limit in the comoving frame does not lead to the identical physical
description as taking the O(v/c) limit in the lab frame. For that reason, we
keep higher order terms in the third line of (15) for compatibility with the
physical description of the O(v/c) Boltzmann equation (2) in the comoving
frame. These higher-order terms can become nonnegligible.
We observe that the expressions (∂lnρ/∂t+2v/r)K
E
and K
E
4πr
2
ρ∂v/∂m
in equations (13) and (14) cancel based on the hydrodynamic continuity
equation
∂lnρ
∂t
+
2v
r
= −4πr
2
ρ
∂v
∂m
. (16)
Similarly, the terms involving (J
E
−K
E
)v/r cancel. As these cancelling terms
are of O(v/c) and proportional to the neutrino density, they grow during a
core collapse simulation and become quite large at and after bounce. Hence,
it is important for a satisfactory global energy conservation to guarantee
their cancellation in the finite difference representation as well. Identifying
the origin of the terms (∂lnρ/∂t+2v/r)K
E
and K
E
4πr
2
ρ∂v/∂m, we find
that (∂lnρ/∂t+2v/r)K
E
originates from the zeroth moment of the observer
correction
µ
2
∂lnρ
∂t
+
2v
r
−
1 − µ
2
v
r
1
E
2
∂
∂E
E
3
F
, (17)
in the Boltzmann equation (2), and K
E
4πr
2
ρ∂v/∂m originates from the first
moment of the space propagation term, µ∂
4πr
2
ρF
/∂m, in the same equa-
tion. The terms
J
E
− K
E
v/r stem from the zeroth moment of the same
observer correction (17) and the first moment of the angular propagation
term ∂
1 − µ
2
F
/ (r∂µ) in the Boltzmann equation (2). The requirement
of global energy conservation in the lab frame therefore imposes interdepen-
dencies on the finite differencing of the space propagation term, the angular
propagation term, and the terms describing the observer corrections [17].
In particular, to determine the “matched” finite differencing for
A ≡ µ
2
∂lnρ
∂t
+
2v
r
(18)
B ≡ (1 − µ
2
)
v
r
(19)
we begin by multiplying the discrete representation of the left-hand side of the
Boltzmann equation (2) (sans the terms describing the observer corrections)
by 1 + µ¯v
i+1
(in what follows, unless otherwise specified the indices are i
, j
,
and k
):
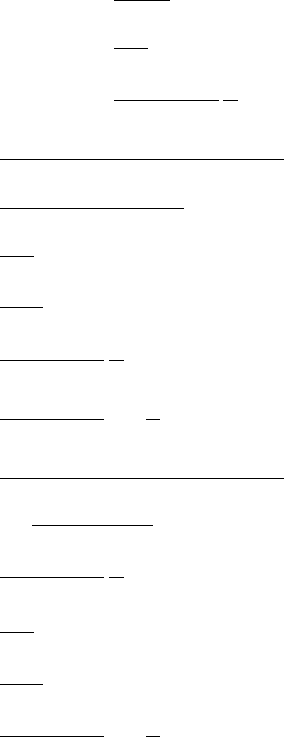
Neutrino Transport in Core Collapse Supernovae 49
(1 + µ¯v
i+1
)E
F −
¯
F
cdt
(20)
+(1+µ¯v
i+1
)E
4πµ
dm
[¯r
2
i+1
¯ρ
i+1
F
i+1
− ¯r
2
i
¯ρ
i
F
i
]
+(1+µ¯v
i+1
)E
3(¯r
2
i+1
− ¯r
2
i
)
2(¯r
3
i+1
− ¯r
2
3
)
1
w
[ζ
j+1
F
j+1
− ζ
j
F
j
]
=
(1 + µv
i+1
)EF − (1 + µ¯v
i+1
)E
¯
F
cdt
−
µv
i+1
EF − µ¯v
i+1
EF
cdt
+
4πµ
dm
[(1 + µ¯v
i+1
)E¯r
2
i+1
¯ρ
i+1
F
i+1
− (1 + µ¯v
i
)E¯r
2
i
¯ρ
i
F
i
]
−
4πµ
2
dm
[¯v
i+1
¯r
2
i
¯ρ
i
EF
i
− ¯v
i
¯r
2
i
¯ρ
i
EF
i
]
+
3(¯r
2
i+1
− ¯r
2
i
)
2(¯r
3
i+1
− ¯r
2
3
)
1
w
[ζ
j+1
EF
j+1
− ζ
j
EF
j
]
+
3(¯r
2
i+1
− ¯r
2
i
)
2(¯r
3
i+1
− ¯r
2
3
)
¯v
i+1
1
w
[µζ
j+1
EF
j+1
− µζ
j
EF
j
]
=
(1 + µv
i+1
)EF − (1 + µ¯v
i+1
)E
¯
F
cdt
− EF
µv
i+1
− µ¯v
i+1
cdt
+
3(¯r
2
i+1
− ¯r
2
i
)
2(¯r
3
i+1
− ¯r
2
3
)
1
w
[ζ
j+1
EF
j+1
− ζ
j
EF
j
]
+
4πµ
dm
[(1 + µ¯v
i+1
)E¯r
2
i+1
¯ρ
i+1
F
i+1
− (1 + µ¯v
i
)E¯r
2
i
¯ρ
i
F
i
]
−
4πµ
2
dm
¯r
2
i
¯ρ
i
EF
i
[¯v
i+1
− ¯v
i
]
+
3(¯r
2
i+1
− ¯r
2
i
)
2(¯r
3
i+1
− ¯r
2
3
)
¯v
i+1
1
w
[µζ
j+1
EF
j+1
− µζ
j
EF
j
] .
As noted, the total energy equation is obtained when summing equations
(13) and (14) and then integrating over m (the integration in µ and E has
already taken place). In this sequence of integrations, the term involving A
in (13) cancels with the term −4πr
2
ρK
E
dv/dm in equation (14). We must
ensure this happens in the discrete limit. Identifying the appropriate velocity
gradient term in (21) and focusing on the appropriate integration (in this case,
over m), we require that (below, the term involving A comes from the zeroth
moment of first term in the observer correction (17) after an integration by
parts; the term involving the velocity gradient is the next to last term in
(21), corresponding to the first moment of the spatial propagation term in
the Boltzmann equation (2)):
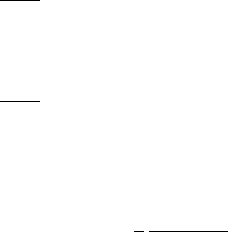
50 A. Mezzacappa et al.
i=1,imax−1
A
i
F
i
dm
i
−
i=1,imax−1
4πµ
2
¯r
2
i
¯ρ
i
F
i
(¯v
i+1
− ¯v
i
)
=
i=1,imax−1
A
i
F
i
dm
i
−
i=1,imax−1,j≤jmax/2
4πµ
2
¯r
2
i
(β
i
¯ρ
i
F
i
+(1− β
i
)¯ρ
i
−1
F
i
−1
)(¯v
i+1
− ¯v
i
)
−
i=1,imax−1,j≥jmax/2+1
4πµ
2
¯r
2
i
(β
i
¯ρ
i
−1
F
i
−1
+(1− β
i
)¯ρ
i
F
i
)(¯v
i+1
− ¯v
i
)
=
i=1,imax−1
A
i
F
i
dm
i
−
i=1,imax−1,j≤jmax/2
4πµ
2
¯r
2
i
(¯v
i+1
− ¯v
i
)β
i
¯ρ
i
F
i
−
i=1,imax−2,j≤jmax/2
4πµ
2
¯r
2
i+1
(¯v
i+2
− ¯v
i+1
)(1 − β
i+1
)¯ρ
i
F
i
−
i=1,imax−1,j≥jmax/2+1
4πµ
2
¯r
2
i
(¯v
i+1
− ¯v
i
)(1 − β
i
)¯ρ
i
F
i
−
i=1,imax−2,j≥jmax/2+1
4πµ
2
¯r
2
i+1
(¯v
i+2
− ¯v
i+1
)β
i+1
)¯ρ
i
F
i
=0, (21)
which gives [17]
A
i
=4πµ
2
¯ρ
i
dm
i
(¯r
2
i
(¯v
i+1
− ¯v
i
)β
i
+¯r
2
i+1
(¯v
i+2
− ¯v
i+1
)(1 − β
i+1
)) (22)
for j ≤ jmax/2and
A
i
=4πµ
2
¯ρ
i
dm
i
(¯r
2
i
(¯v
i+1
− ¯v
i
)(1 − β
i
)+¯r
2
i+1
(¯v
i+2
− ¯v
i+1
)β
i+1
) (23)
for j ≥ jmax/2+1.
Similarly, defining B
according to
B ≡
3
2
¯r
2
i+1
− ¯r
2
i
¯r
3
i+1
− ¯r
3
i
¯v
i+1
B
, (24)
and again focusing on the appropriate integration (in this case, over µ), we
require that (below, the term involving B
comes from the zeroth moment of
the second term in the observer correction (17), after an integration by parts;
the second term is the last term in (21), corresponding to the first moment
of the angular propagation term):

Neutrino Transport in Core Collapse Supernovae 51
0=
j=1,jmax
B
F
j
w
j
+
j=1,jmax
2
w
j
[µ
j
α
j+1
F
j+1
− µ
j
α
j
F
j
]w
j
=
j=1,jmax
B
F
j
w
j
+
j=1,jmax
2[µ
j
α
j+1
(γF
j
+(1− γ)F
j
+1
)
− µ
j
α
j
(γF
j
−1
+(1− γ)F
j
)]
=
j=1,jmax
B
F
j
w
j
+
j=1,jmax
2[µ
j
α
j+1
γ − µ
j
α
j
(1 − γ)]F
j
+
j=2,jmax
2µ
j
−1
α
j
(1 − γ)F
j
+
j=1,jmax−1
(−2)µ
j
+1
α
j+1
γF
j
=
j=1,jmax
B
F
j
w
j
+
j=1,jmax
2γα
j+1
(µ
j
− µ
j
+1
)F
j
+
j=1,jmax
2(1 − γ)α
j
(µ
j
−1
− µ
j
)F
j
, (25)
which gives [17]
B
j
=
3
2
¯r
2
i+1
− ¯r
2
i
¯r
3
i+1
− ¯r
3
i
¯v
i+1
2γα
j+1
µ
j
+1
− µ
j
w
j
+2(1− γ)α
j
µ
j
− µ
j
−1
w
j
. (26)
3.6 Frequency Shift from Observer Motion
For comoving observers, we must account for the observed shift in the fre-
quency of a neutrino measured by two neighboring observers moving with
different velocities. Motivated by the definitions (18) and (19), the observer
correction, (17), can be written as
0=E
3
∂F
∂t
E
+
µ
2
A − B
E
∂
∂E
E
3
F
. (27)

52 A. Mezzacappa et al.
It has been found in [10] and [14] that (27) has an analytical solution. One
may write [14] the prefactor in (27) as the time derivative of the quantity
R
f
= r
(
3µ
2
−1
)
ρ
(
µ
2
)
:
∂lnR
f
∂t
= µ
2
A − B.
If we transform from the “Eulerian” variable, x = E, to the “Lagrangian”
variable, y = E/R
f
, (27) becomes
0=
∂
∂t
E
3
F
E
+
∂R
f
R
2
f
∂t
E × R
f
∂
∂E
E
3
F
=
∂
∂t
E
3
F
E
−
∂ [E/R
f
]
∂t
E
∂
E
3
F
∂ [E/R
f
]
=
∂
∂t
E
3
F
E/R
f
.
For a small section of energy phase space E
2
∆E =
E
3
2
− E
3
1
/3, this rela-
tionship leads to
∂
∂t
E
2
F∆E
E/R
f
=0. (28)
The validity of (28) for arbitrary neutrino distributions F leads to the fol-
lowing interpretation: The neutrinos initially residing in the energy interval
E
2
∆E move, according to the observer correction, along constant E/R
f
in
the phase space of a comoving observer. This allows us to determine the evo-
lution of any neutrino property. For example, the neutrino specific energy in
this phase space interval, d = E
3
F∆E, evolves according to
∂
∂t
E
3
F∆E
E/R
f
= E
2
F∆E
∂E
∂t
E/R
f
=
∂lnR
f
∂t
d . (29)
A finite difference representation of (28) and (29) has been given in [14].
Consider a neutrino energy group k
, with neighboring groups k
+ dk, dk =
±1. Equation (28) tells us that the number of neutrinos before the comoving
observer correction, F
i
,j
,k
E
2
k
dE
k
, is equal to the number of neutrinos after
the correction. The distribution after the correction has a diminished number
of neutrinos F
i
,j
,k
E
2
k
dE
k
− n
−
i
,j
,k
in group k
and an additional number
of neutrinos n
+
i
,j
,k
+dk
in the neighboring group k
+ dk,
F
i
,j
,k
E
2
k
dE
k
−
F
i
,j
,k
E
2
k
dE
k
− n
−
i
,j
,k
+ n
+
i
,j
,k
+dk
=0. (30)
Equation (29) defines a similar correction for the specific neutrino energy in
group k
F
i
,j
,k
E
3
k
dE
k
−
F
i
,j
,k
E
3
k
dE
k
− E
k
n
−
i
,j
,k
+ E
k
+dk
n
+
i
,j
,k
+dk
= −
µ
2
j
A
i
,k
− B
i
,j
,k
F
i
,j
,k
E
3
k
dE
k
dt . (31)

Neutrino Transport in Core Collapse Supernovae 53
where A
i
,k
and B
i
,j
,k
are given by (22), (23), and (26). Equations (30)
and (31) uniquely define the solution
n
−
i
,j
,k
=
µ
2
j
A
i
,k
− B
i
,j
,k
dE
k
E
k
+dk
− E
k
E
3
k
F
i
,j
,k
dt
n
+
i
,j
,k
= n
−
i
,j
,k
−dk
, (32)
which leads, by the update F
i
,j
,k
=F
i
,j
,k
+
n
+
i
,j
,k
− n
−
i
,j
,k
/
E
2
k
dE
k
,
to the following finite difference representation of the frequency shift term in
the Boltzmann equation (2):
1
E
2
k
dE
k
×
µ
2
j
A
i
,k
−dk
− B
i
,j
,k
dE
k
−dk
E
k
− E
k
−dk
E
3
k
−dk
F
i
,j
,k
−dk
−
µ
2
j
A
i
,k
− B
i
,j
,k
dE
k
E
k
+dk
− E
k
E
3
k
F
i
,j
,k
. (33)
3.7 Angular Aberration from Observer Motion
We are left with the task of finding a finite difference representation for the
angular aberration in (2). Because the global energy depends on (1 + u
i
µ
j
)
F
i
,j
,k
, any correction to the neutrino propagation direction also affects en-
ergy conservation. Therefore, it is desirable to construct a numerical im-
plementation of angular aberration that conserves the specific neutrino lu-
minosity µ
j
F
i
,j
,k
w
j
[17], much like our numerical implementation of the
frequency shift preserved the specific neutrino energy.
With ζ =1− µ
2
, the angular aberration term can be rewritten as
∂F
∂t
µ
=(A + B/ζ)
∂
∂µ
[ζµF] . (34)
As before, we search for an analytic solution. For the quantity R
a
= r
3
ρ,we
find
dlnR
a
dt
= A + B/ζ .
It is now possible to rewrite (34) in terms of the “Lagrangian” variable y =
ζ
−1/2
µ/R
a
instead of the “Eulerian” variable x = µ. After a multiplication
by ζµ, (34) becomes:
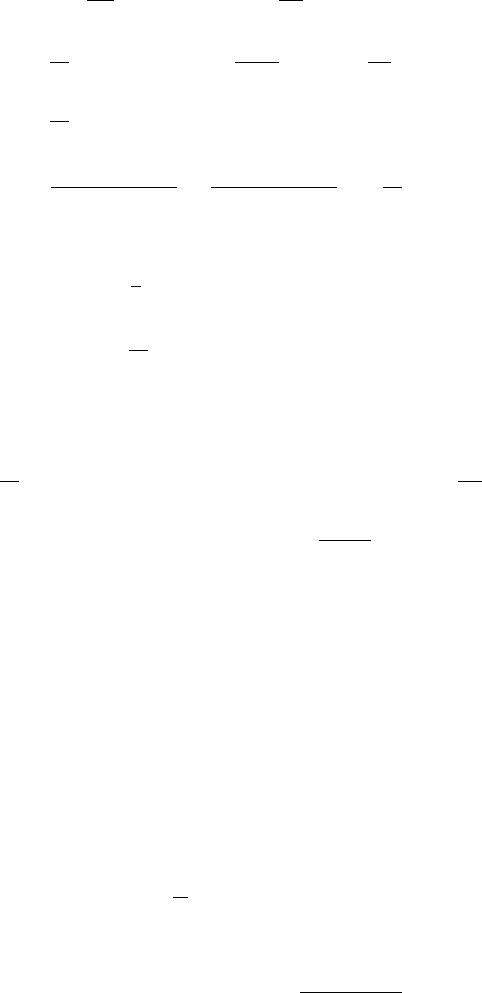
54 A. Mezzacappa et al.
0=ζµ
∂F
∂t
µ
+ α (A + B/ζ)
∂
∂µ
[ζµF]
=
∂
∂t
[ζµF]
µ
+ ζ
−1/2
µ
∂R
a
R
2
a
∂t
× ζ
3/2
R
a
∂
∂µ
[ζµF]
=
∂
∂t
[ζµF]
µ
−
∂
ζ
−1/2
µ/R
a
∂t
µ
∂ [ζµF]
∂
ζ
−1/2
µ/R
a
=
∂
∂t
[ζµF]
ζ
−1/2
µ/R
a
.
And once again, the interpretation is clear. The neutrinos initially residing
in the interval
1 − 3µ
2
∆µ = ζ
2
µ
2
−ζ
1
µ
1
are shifted by angular aberration
along constant µ/
√
ζR
a
in the phase space of a comoving observer:
∂
∂t
1 − 3µ
2
F∆µ
ζ
−1/2
µ/R
a
=0. (35)
We may now evaluate the change in other neutrino properties; for example,
the specific luminosity, d =
1 − 3µ
2
µF ∆µ,
∂
∂t
1 − 3µ
2
µF ∆µ
ζ
−1/2
µ/R
a
=
1 − 3µ
2
F∆µ
∂µ
∂t
ζ
−1/2
/R
a
= ζ
∂lnR
a
∂t
d . (36)
We identify the bin size
1 − 3µ
2
j
∆µ
j
= w
j
with our Gaussian quadrature
weights. Equation (35) leads to the condition for number conservation:
F
i
,j
,k
w
j
−
F
i
,j
,k
w
j
− n
−
i
,j
,k
+ n
+
i
,j
+dj, k
=0
and (36) leads to a prescription for the numerical evolution of the specific
luminosity:
F
i
,j
,k
µ
j
w
j
−
F
i
,j
,k
µ
j
w
j
− µ
j
n
−
i
,j
,k
+ µ
j
+dj
n
+
i
,j
+dj, k
= −(ζ
j
A
i
,k
+ B
i
,j
,k
) F
i
,j
,k
µ
j
w
j
dt .
where dj = ±1. The change in the neutrino distribution from angular aber-
ration is then:
F
i
,j
,k
= F
i
,j
,k
+
n
+
i
,j
,k
− n
−
i
,j
,k
/w
j
(37)
with
n
−
i
,j
,k
=(A
i
,k
+ B
i
,j
,k
/ζ
j
)
w
j
µ
j
+dj
− µ
j
ζ
j
µ
j
F
i
,j
,k
dt
n
+
i
,j
,k
= n
−
i
,j
−dj, k
.

Neutrino Transport in Core Collapse Supernovae 55
This leads to the following finite difference representation of the angular
aberration term in the Boltzmann equation (2):
1
w
j
(A
i
,k
+ B
i
,j
−dj, k
/ζ
j
−dj
)
w
j
−dj
µ
j
− µ
j
−dj
ζ
j
−dj
µ
j
−dj
F
i
,j
−dj, k
− (A
i
,k
+ B
i
,j
,k
/ζ
j
)
w
j
µ
j
+dj
− µ
j
ζ
j
µ
j
F
i
,j
,k
. (38)
We apply the aberration corrections with dj =+1forµ ≤ 0anddj = −1for
µ>0. This is not upwind differencing and, therefore, runs the risk of produc-
ing negative neutrino distribution functions. However, there are three reasons
to accept this shortcoming: (i) The angular aberration correction is generally
small, with the exception of aberration in the vicinity of strong shocks with
large velocity gradients. (ii) As long as the angle-integrated neutrino density
is positive, transiently negative contributions from backward directions on the
Gaussian angular grid (µ<0) allow the computer representation of strongly
forward peaked neutrino fluxes that would not be representable with positive
neutrino distribution functions on a grid with limited angles µ
max
< 1. (iii)
The chosen direction of dj guarantees that no neutrinos are shifted off the
grid. This is a prerequisite for number and energy conservation.
4 The General Case: The Multidimensional Neutrino
Transport Equations
As the previous sections illustrate, one of the greatest challenges encoun-
tered when developing the numerical methods to obtain a physically reliable
solution of the neutrino transport equations in core collapse supernovae is to
achieve simultaneous lepton number and energy conservation or balance,the
former for massless neutrinos and Newtonian gravity, where lepton number is
conserved and where the concept of a conserved energy can be defined in mul-
tiple spatial dimensions, the latter for the general relativistic case in two and
three spatial dimensions. The first step in meeting this challenge is to derive
the conservative lepton number and energy conservation/balance equations,
which at a more fundamental level means finding the corresponding evolved
variables that naturally lend themselevs to a conservative decription of the
neutrino radiation field. As we will see, both the conservation/balance equa-
tions and the fundamental variables can be extracted from the underlying
kinetic theory at a point in the theory where the fundamental physical laws
are manifestly conservative [20].
The distribution function f represents the density of neutrinos in phase
space. The phase space for neutrinos of definite mass m, M
m
, is filled with
trajectories
x
µ
(λ),p
ˆ
i
(λ)
, or “states”. As a collection of neutrinos evolves,
the number of neutrinos in each state changes due to collisions. If one consid-
ers a 6-dimensional hypersurface Σ in M
m
, the ensemble-averaged number

56 A. Mezzacappa et al.
N[Σ] of occupied states crossing Σ is
N[Σ]=
Σ
fω , (39)
where ω is the surface element.
An equation governing the evolution of the distribution function is ob-
tained by considering a closed 6-dimensional hypersurface ∂D bounding a
region D in M
m
. The net number of occupied states emerging from D is,
from (39) and the generalized Stokes’ theorem,
N[∂D]=
∂D
fω =
D
d(fω) . (40)
This equation relates a volume integral to a surface integral and is key to ob-
taining conservative formulations of kinetic theory. In fact, in rushing head-
long in deriving the general relativistic Boltzmann equation
p
ˆµ
Λ
¯µ
ˆµ
e
µ
¯µ
∂f
∂x
µ
− Γ
ˆν
ˆρ ˆµ
p
ˆρ
∂f
∂p
ˆν
= C[f] . (41)
from (40), (40) is easily overlooked. Here Λ
¯µ
µ
is the Lorentz boost between
the orthonormal lab and (fluid) comoving frames and e
µ
¯µ
is the tetrad trans-
formation between the coordinate basis and the orthonormal lab frame. The
integrand on the right-hand side of (40), d(fω), is in conservative form. Ma-
nipulating it just enough to bring it into the form d(fω)=F [f]Ω,whereΩ is
the volume element in phase space, yields a conservative formulation of neu-
trino number kinetics, and manipulating the exterior derivative d(v
µ
p
µ
fω),
for an arbitrary timelike vector v
µ
, yields a conservative formulation of neu-
trino four-momentum kinetics. Defining the specific neutrino number flux
vector
N
µ
≡L
µ
ˆµ
p
ˆµ
f (42)
and the specific neutrino stress-energy tensor
T
µν
≡L
µ
ˆµ
L
ν
ˆν
p
ˆµ
p
ˆν
f, (43)
where L
ˆµ
µ
= e
µ
¯µ
Λ
¯µ
µ
is the transformation to the comoving frame, the conser-
vative kinetic equations for neutrino number and four-momentum are:
1
√
−g
∂
∂x
µ
√
−gN
µ
− E(p)
det
∂p
∂u
−1
∂
∂u
ˆ
i
1
E(p)
det
∂p
∂u
Γ
ˆ
j
ˆµˆν
p
ˆν
∂u
ˆ
i
∂p
ˆ
j
L
ˆµ
µ
N
µ
= C[f] , (44)
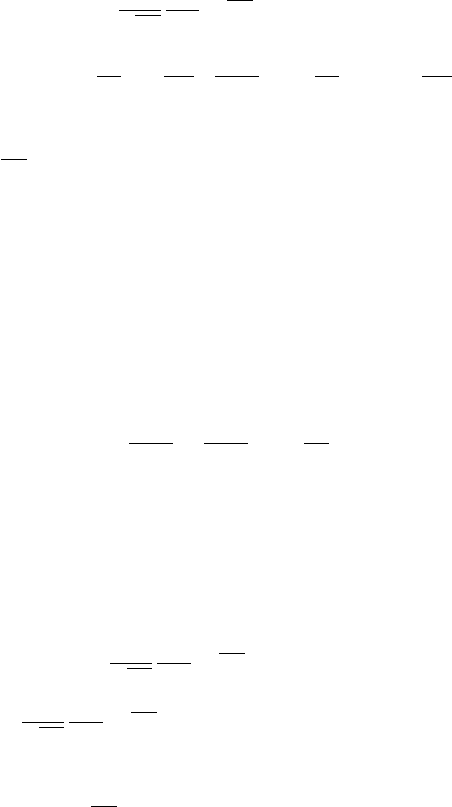
Neutrino Transport in Core Collapse Supernovae 57
1
√
−g
∂
∂x
ν
√
−gT
µν
+ Γ
µ
νρ
T
νρ
− E(p)
det
∂p
∂u
−1
∂
∂u
ˆ
i
1
E(p)
det
∂p
∂u
Γ
ˆ
j
ˆν ˆρ
p
ˆρ
∂u
ˆ
i
∂p
ˆ
j
L
ˆν
ν
T
µν
= F
µ
ν
N
ν
+ L
µ
ˆµ
p
ˆµ
C[f] . (45)
where
√
−g is the determinant of the spacetime metric. The adjective “spe-
cific” often denotes a quantity measured per unit mass, but in this context
we use it to denote the neutrino flux and stress-energy in a given invariant
momentum space volume element. While the distribution function f obeys
the Boltzmann equation (41), the specific neutrino number flux and stress-
energy satisfy the conservative equations (44) and (45). In stating that (44)
and (45) constitute conservative formulations of neutrino kinetics, we mean
that the connection to the corresponding balance equations is transparent.
We can use elementary calculus to form the familiar invariant momentum
space volume element
d
3
p
E(p)
=
1
E(p)
det
∂p
∂u
d
3
u, (46)
where a transformation from orthonormal momentum components
p
ˆ
i
to
some other set of coordinates (e.g., momentum space spherical coordinates
u
ˆ
i
= {|p|,ϑ,ϕ}) has been performed. Multiplying equations (44) and (45)
by (46) and integrating, the terms with momentum space derivatives are ob-
viously transformed into vanishing surface terms. The results are the balance
equations
1
√
−g
∂
∂x
µ
√
−gN
µ
=
C[f]π
m
, (47)
1
√
−g
∂
∂x
µ
√
−gT
νµ
= −Γ
ν
ρµ
T
ρµ
+
C[f]L
ν
ˆν
p
ˆν
π
m
. (48)
for total neutrino number and 4-momentum, where N
µ
and T
µν
are the
neutrino number current and stress-energy tensor, respectively. In the above
equations, π
m
=
√
−g
0ijk
dp
i
∧ dp
j
∧ dp
k
//6|p
0
| is the invariant volume ele-
ment on a mass shell corresponding to the mass m in the tangent space [20].
In the previous sections, we presented a detailed account of how one ob-
tains a conservative differencing for the equation governing the evolution of
the specific neutrino distribution function for spherically symmetric flows.
Working with comoving frame neutrino four momenta, the conservation of
total lab frame energy required a matching of the finite differencing of the ra-
dial, angular, and energy advection terms in this equation. One can, of course,
take a different approach. While the use of comoving frame four momenta for
the neutrinos is a prerequisite given the neutrino interactions with the stellar
core, which are most naturally and most simply expressed in terms of these
