Greenwood D.T. Advanced Dynamics

Подождите немного. Документ загружается.

69 Problems

1.15. A massless disk of radius r has a particle of mass m attached at a distance l from its

center. The disk rolls without slipping on a horizontal ﬂoor. Then, for some position

angle θ, a horizontal impulse

F is applied at the highest point A on the disk. Solve

for the change ω in angular velocity, as well as the constraint impulse components

and

Figure P 1.15.

1.16. Consider the system of Example 1.13 on page 55. Assume the same initial conditions

and the same applied impulse

F. Now suppose that Coulomb friction is added for the

sliding of particle B relative to the ﬂoor. (a) Assuming a friction coefﬁcient µ,solve

for the values of

x and

θ immediately after the impulse. (b) What is the minimum

value of µ such that there is no sliding?

1.17. Two particles, each of mass m, are connected by a massless cord of length

πr on

a ﬁxed horizontal cylinder of radius r. There is a coefﬁcient of friction µ for sliding

of the particles on the cylinder. (a) Obtain the equation of motion, assuming

θ>0

and the particles remain in contact with the cylinder. (b) Solve for the tension P in

the cord as a function of θ. Assume that 0 ≤ θ ≤

π and 0 <µ<1.

Figure P 1.17.

70 Introduction to particle dynamics

1.18. A particle P of mass m can slide without friction on a rigid ﬁxed wire. It is connected

to a ﬁxed point O through a linear damper with a damping coefﬁcient c. Assuming

the initial conditions x(0) = 0,

x(0) = v

, solve for the initial velocity v

which will

cause the particle to stop at x = h.

Figure P 1.18.

1.19. Two particles, each of mass m, are connected by a rigid massless rod of length l. Parti-

cle 1 can slide without friction on a ﬁxed straight wire. (a) Using (x,θ) as generalized

coordinates for motion in the horizontal plane, solve for

θ, and P as functions

of (θ,

θ) where P is the tensile force in the rod. (b) Assume the initial conditions

x(0) = 0,

x(0) = 0,θ(0) = 0,

θ(0) = v

/l. Solve for

x and

θ as functions of θ.

Figure P 1.19.

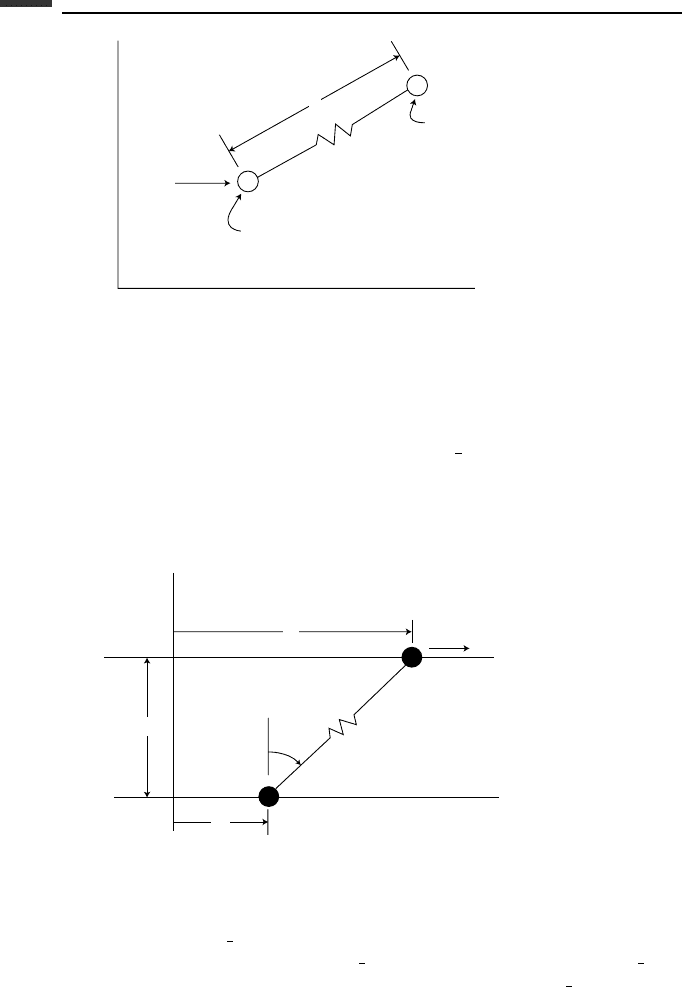
1.20. Two particles, connected by a spring of stiffness k and unstressed length L, move in

the horizontal xy-plane. A force F in the x direction is applied to the ﬁrst particle.

(a) Using (x

, y

, x

, y

) as coordinates, obtain the four differential equations of

motion. (b) Now introduce a constraint on the second particle given by x

= y

Eliminate y

and write equations of motion for x

, y

, and x

71 Problems

, y

)

, y

)

Figure P 1.20.

1.21. Two particles, each of mass m, can slide on smooth parallel ﬁxed wires which are

separated by a distance h. The particles are connected by a linear spring of stiffness

k and unstressed length h. (a) Assume the initial conditions x

(0) = x

(0) = 0 and

(0) =

(0) = 0. At t = 0, a constant force F =

kh is applied to the ﬁrst particle.

In the motion which follows, solve for the maximum value of θ . (b) Assume the

initial conditions θ (0) = θ

and

θ(0) = 0. Find the value of θ such that it remains

constant during the motion.

Figure P 1.21.

1.22. A ﬂexible inextensible rope of uniform linear density ρ and length L is initially at

rest with y(0) =

L. (a) Find the differential equation for y in the following two

cases: (1) upward motion with F =

ρ Lg; (2) downward motion with F =

ρ Lg.

(b) Show that in each case the magnitude of the energy loss rate is

ρ|

72 Introduction to particle dynamics

L−x

Figure P 1.22.

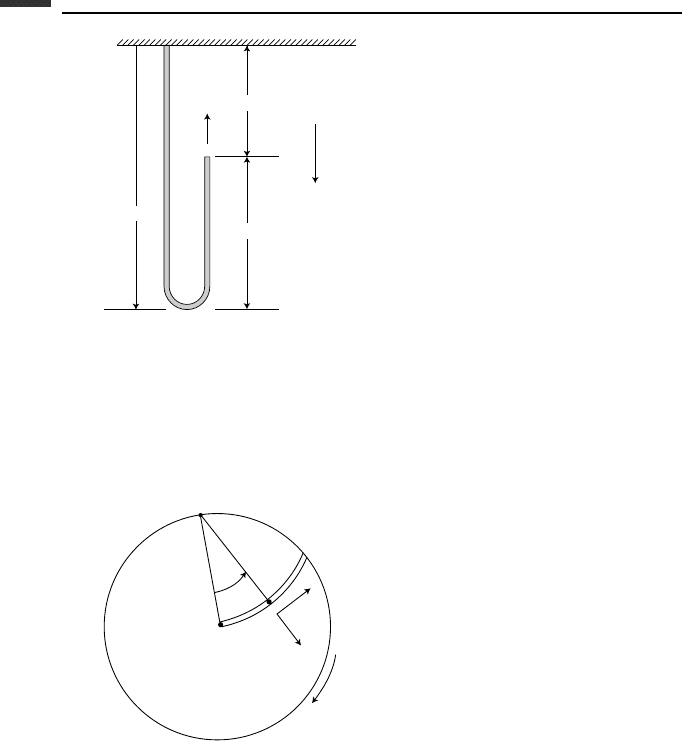
1.23. A particle P of mass m can slide without friction in a slot having the form of an arc of

radius r which is cut in a circular impeller that rotates with a constant angular velocity

. (a) Write the differential equation of motion in terms of the relative position angle

θ. (b) Assuming that the particle is released from rest at θ = 0, ﬁnd the value of

θ as the

particle leaves the impeller. (c) What is the force on the particle just before it leaves?

O′

Figure P 1.23.

Lagrange’s and Hamilton’s equations

In our study of the dynamics of a system of particles, we have been concerned primarily

with the Newtonian approach which is vectorial in nature. In general, we need to know

the magnitudes and directions of the forces acting on the system, including the forces of

constraint. Frequently the constraint forces are not known directly and must be included as

additional unknown variables in the equations of motion. Furthermore, the calculation of

particle accelerations can present kinematical difﬁculties.

An alternate approach is that of analytical dynamics, as represented by Lagrange’s equa-

tions and Hamilton’s equations. These methods enable one to obtain a complete set of

equations of motion by differentiations of a single scalar function, namely the Lagrangian

function or the Hamiltonian function. These functions include kinetic and potential ener-

gies, but ideal constraint forces are not involved. Thus, orderly procedures for obtaining the

equations of motion are available and are applicable to a wide range of problems.

2.1 D’Alembert’s principle and Lagrange’s equations

D’Alembert’s principle

Let us begin with Newton’s law of motion applied to a system of N particles. For the ith

particle of mass m

and inertial position r

,wehave

+ R

− m

¨r

= 0 (2.1)

where F

is the applied force and R

is the constraint force. Now take the scalar product

with a virtual displacement δr

and sum over i. We obtain



i=1

(

+ R

− m

¨r

)

· δr

= 0 (2.2)

This result is valid for arbitrary δrs; but now assume that the δrs satisfy the instantaneous

or virtual constraint equations, namely,



i=1

(x , t )δx

= 0(j = 1,...,m) (2.3)

74 Lagrange’s and Hamilton’s equations

where the δxs are the Cartesian components of the δrs. The virtual work of the constraint

forces must vanish, that is,



i=1

· δr

= 0 (2.4)

Then (2.2) reduces to



i=1

(

− m

¨r

)

· δr

= 0 (2.5)

This important result is the Lagrangian form of d’Alembert’s principle. It states that the

virtual work of the applied forces plus the inertia forces is zero for all virtual displacements

satisfying the instantaneous constraints, that is, with time held ﬁxed. The forces due to ideal

constraints do not enter into these equations. This important characteristic will be reﬂected

in various dynamical equations derived using d’Alembert’s principle, including Lagrange’s

and Hamilton’s equations.

In terms of Cartesian coordinates, d’Alembert’s principle has the form



k=1

(

− m

)

δx

= 0 (2.6)

where the δxs satisfy (2.3). Equation (2.6) is valid for any set of δx s which satisfy the

instantaneous constraints. There are (3N − m) independent sets of δx s, each being conven-

iently expressed in terms of δx

ratios. This results in (3N − m) equations of motion. An

additional m equations are obtained by differentiating the constraint equations of (1.203)

or, in this case,



i=1

+ a

= 0(j = 1,...,m) (2.7)

with respect to time. Altogether, there are now 3N second-order differential equations which

can be solved, frequently by numerical integration, for the xs as functions of time. Note

that the constraint forces have been eliminated from the equations of motion.

Example 2.1 A particle of mass m can move without friction on the inside surface of a

paraboloid of revolution (Fig. 2.1)

φ = x

+ y

− z = 0 (2.8)

under the action of a uniform gravitational ﬁeld in the negative z direction. We wish to

ﬁnd the differential equations of motion using d’Alembert’s principle. The applied force

components are

= 0, F

=−mg (2.9)

75 D’Alembert’s principle and Lagrange’s equations

Figure 2.1.

In order to obtain the constraint equation for the virtual displacements, ﬁrst write (2.8)

in the differential form

φ = 2x

x +2y

y −

z = 0 (2.10)

The instantaneous constraint equation, obtained using (2.3), is

2x δx +2yδy − δz = 0 (2.11)

We need to ﬁnd 3N − m = 2 independent virtual displacements which satisfy (2.11). We

can take

δy = 0,δz = 2xδx (2.12)

and

δx = 0,δz = 2yδy (2.13)

Then d’Alembert’s principle, (2.6), results in

[

−m

x −2mx(

z + g)

]

δx = 0 (2.14)

[

−m

y − 2my(

z + g)

]

δy = 0 (2.15)

Now δx is freely variable in (2.14), as is δy in (2.15), so their coefﬁcients must equal zero.

Thus, after dividing by −m, we obtain

x +2x (

z + g) = 0 (2.16)

y + 2y(

z + g) = 0 (2.17)

These are the dynamical equations of motion. A kinematical second-order equation is

obtained by differentiating (2.10) with respect to time, resulting in

x +2y

y −

z + 2

+ 2

= 0 (2.18)

76 Lagrange’s and Hamilton’s equations

Equations (2.16)–(2.18) can be solved for

y and

z, which are then integrated to give the

particle motion as a function of time.

Lagrange’s equations

Consider a system of N particles. Let us begin the derivation with d’Alembert’s principle

expressed in terms of Cartesian coordinates, that is,



k=1

(

− m

)

δx

= 0 (2.19)

The F

s are applied force components and the δxs are consistent with the instantaneous

constraints, as given in (2.3). We wish to transform to generalized coordinates. Recall that

δx



i=1

∂x

∂q

δq

(k = 1,...,3N ) (2.20)

Hence, we obtain



i=1



k=1



∂x

∂q

− m

∂x

∂q



δq

= 0 (2.21)

where the δqs conform to any constraints. But since x

= x

(q, t),



i=1

∂x

∂q

∂x

∂t

(2.22)

and we see that

∂

∂x

∂q

(2.23)

Furthermore,



∂x

∂q





j=1

∂

∂q

∂

∂t ∂q

∂

∂q

(2.24)

The kinetic energy of the system is

T =



k=1

(2.25)

and the generalized momentum p

∂T

∂



k=1

∂



k=1

∂x

∂q

(2.26)

Therefore, we obtain



∂T

∂





k=1

∂x

∂q



k=1

∂

∂q

(2.27)

77 D’Alembert’s principle and Lagrange’s equations

However, from (2.25),

∂T

∂q



k=1

∂

∂q

(2.28)

so we ﬁnd that



k=1

∂x

∂q



∂T

∂



−

∂T

∂q

(2.29)

This result is the negative of the generalized inertia force Q

∗

. In other words,

∗

=−



∂T

∂



∂T

∂q

(2.30)

From (1.240), we recall that the generalized applied force is



k=1

∂x

∂q

(2.31)

Then d’Alembert’s principle, as written in (2.21) results in



i=1

+ Q

∗

)δq

= 0 (2.32)

for all δqs satisfying any constraints. Thus, the virtual work of the applied plus the inertial

generalized forces is equal to zero.

Using (2.30) and (2.31) with a change of sign, (2.32) takes the form



i=1





∂T

∂



−

∂T

∂q

− Q



δq

= 0 (2.33)

where, again, the δqs satisfy the instantaneous constraints. This is d’Alembert’s principle

expressed in terms of generalized coordinates. We will call it Lagrange’s principle.Itapplies

to both holonomic and nonholonomic systems, requiring only that T and Q

be written as

functions of (q,

q, t). Note that constraint forces do not enter the Q

Now let us assume a holonomic system with independent generalized coordinates. Then

the coefﬁcient of each δq

must be equal to zero. We obtain



∂T

∂



−

∂T

∂q

= Q

(i = 1,...,n) (2.34)

This is the fundamental holonomic form of Lagrange’s equation. It results in n second-order

ordinary differential equations. The Qs are generalized applied forces from any source.

Let us make the further restriction that the Qs are derivable from a potential energy

function V (q, t ) in accordance with

=−

∂V

∂q

(2.35)

78 Lagrange’s and Hamilton’s equations

Now deﬁne the Lagrangian function

L(q,

q, t) = T (q,

q, t) − V (q, t) (2.36)

Then we can write Lagrange’s equation in the standard holonomic form:



∂ L

∂



−

∂ L

∂q

= 0(i = 1,...,n) (2.37)

Equivalently, one can use



∂T

∂



−

∂T

∂q

∂V

∂q

= 0(i = 1,...,n) (2.38)

If a portion of the applied generalized force is not obtained from a potential function, we

can write

=−

∂V

∂q

+ Q



(2.39)

where Q



is the nonpotential part of Q

. Then we obtain Lagrange’s equation in the form



∂ L

∂



−

∂ L

∂q

= Q



(i = 1,...,n) (2.40)



∂T

∂



−

∂T

∂q

=−

∂V

∂q

+ Q



(i = 1,...,n) (2.41)

The basic forms of Lagrange’s equations, given in (2.34) and (2.37) apply to holonomic

systems described in terms of independent generalized coordinates.

When one considers nonholonomic systems, there must be more generalized coordinates

than degrees of freedom. Hence, the generalized coordinates are not completely independent

and, as a result, there will be generalized constraint forces C

which are nonzero, in general.

In terms of the constraint forces acting on the individual particles, we have, similar to

(1.240),



j=1

· γ



k=1

∂x

∂q

(2.42)

where the R

are Cartesian constraint force components.

Let us use the Lagrange multiplier method to evaluate the generalized constraint forces.

First, we note that the virtual work of the constraint forces must equal zero, that is,



i=1

δq

= 0 (2.43)

provided that the δqs satisfy the instantaneous constraints in the form



i=1

δq

= 0(j = 1,...,m) (2.44)