Koren B., Vuik K. (Editors) Advanced Computational Methods in Science and Engineering
Подождите немного. Документ загружается.


Rob F. Remis and Neil V. Budko
with ω
q
∈Ω for q = 1,2,..., Q. Having this data available, we determine the effective
permittivity and conductivity by looking for a minimum of the objective function
F
Ω
k
(ζ ) =
Q
∑
q=1
w
q
|˜u
sc
(ω
q
) −v
sc
k
(ζ ,ω
q
)|
2
|˜u
sc
(ω
q
)|
2
, (23)
where the w
q
≥ 0 are weighting coefficients satisfying the normalization condition
Q
∑
q=1
w
q
= 1,
and v
sc
k
(ζ ,ω
q
) is the kth order reduced-order model for the scattered field at fre-
quency ω
q
. Notice that we have to apply the Lanczos algorithm Q times to obtain
the reduced-order models for the scattered field at the Q different frequencies, since
matrix G and the source and receiver vector are frequency dependent. Furthermore,
we require that the reduced-order models for all frequencies are accurate on the
largest domain of interest, which is determined by the smallest frequency of opera-
tion (see Eq. (4)).
Finally, for completeness we mention that if only the amplitude of the data avail-
able then we can look for a minimizer of the objective function
F
am;Ω
k
=
Q
∑
q=1
w
q
||˜u(ω
q
)|−|v
sc
k
(ζ ,ω
q
) + u
inc
(ω
q
)||
|˜u(ω
q
)|
, (24)
where, again, the w
q
are weighting coefficients (see Remis and Budko [18]).
5 Numerical experiments
In our first set of experiments we consider the scattering setup shown in Figure 2 and
investigate the difference between reflection and transmission data inversion results.
The configuration consists of a homogeneous block and this block is surrounded by
as a source as well. The true medium parameters of the block are given by ε
r
= 4.5
and σ = 5 mS/m. The minimum and maximum permittivity and conductivity values
are taken as ε
r;min
= 1, ε
r;max
= 9, σ
min
= 0, and σ
max
= 10 mS/m. These values
determine our domain of interest. This domain is discretized on a 50-by-50 grid
and consequently we have to evaluate 2500 reduced-order models for each source-
receiver pair. Furthermore, the source operates at a frequency of 36 MHz and the
side length of the block is d = λ .
To obtain reflection data, we first consider a monostatic source-receiver setup,
that is, antenna N acts as a source as well as a receiver. The objective function for
this setup is shown in Figure 3 (top-left). The true medium parameters can be re-
covered from this function, but quite a number of false minima are present as well.
12
four antennas labeled N (North),W (West), E (East), and S (South). Antenna N acts
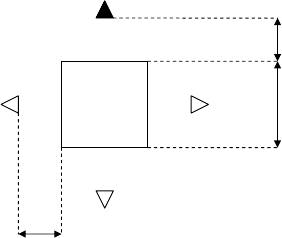
A Model-Order Reduction Approach to Parametric Electromagnetic Inversion
Fig. 2 Scattering configu-
ration with one electric line
source (black triangle) and
four receivers.
d
d/2
d/2
N
S
W E
To obtain partly reflected and partly transmitted data, we keep the source the same
and measure the field with antenna W. The resulting objective function is shown in
Figure 3 (top-right). Again, the true medium parameters can be recovered from this
function and false minima are present. We do observe, however, that the number of
false minima in this case is less than in the previous experiment. Measuring the field
with antenna E produces the same results as with antenna W because of the sym-
metry of the configuration. We therefore do not show the corresponding objective
function.
Finally, to obtain transmission data we measure the field with antenna S. The
objective function obtained with this source-receiver setup is shown in Figure 3 (bot-
tom). Identifying the true medium parameters from this objective function is straight-
forward and there are essentially no false minima present in our domain of interest.
The results of this set of experiments indicate that transmission data provide better
inversion results than reflection data. We have carried out many additional experi-
ments and all these experiments confirm this conclusion.
In our second set of experiments we consider the scattering setup shown in Fig-
ure 4. As opposed to the previous set of experiments, we now keep the source-
receiver unit the same throughout all experiments and use multi-frequency data in-
stead. A square block with side length d is embedded in a vacuum domain and
consists of two concentric square parts. The outer part is characterized by a relative
permittivity ε
r;1
and a conductivity σ
1
, the inner part has a relative permittivity ε
r;2
and a conductivity σ
2
. The source and receiver are located 2 cm apart and are located
a distance d/2 above the object (see Figure 4).
In our first experiment we operate at a frequency of 36 MHz. The wavelength in
vacuum corresponding to this frequency is denoted by λ and for the side length d of
the object we take d = λ . Initially, we consider a homogeneous block with medium
parameters σ
1
= σ
2
= 7.5 mS/m and ε
r;1
= ε
r;2
= 5. The minimum and maximum
relative permittivity and conductivity values are taken to be ε
r;min
= 1, ε
r;max
= 6,
σ
min
= 0 mS/m, and σ
max
= 10 mS/m. Figure 5 (left) shows the base 10 logarithm
13

Rob F. Remis and Neil V. Budko
2 4 6 8
0
2
4
6
8
10
x 10
−3
−8
−6
−4
−2
0
2 4 6 8
0
2
4
6
8
10
x 10
−3
−10
−8
−6
−4
−2
0
2 4 6 8
0
2
4
6
8
10
x 10
−3
−10
−8
−6
−4
−2
0
2
Fig. 3 Base 10 logarithm of the objective function on the domain of interest with antenna N acting
as a source and antenna N acting as receiver (top-left), antenna W acting as a receiver (top-right),
and antenna S acting as a receiver (bottom). The object is homogeneous and has a side length d = λ ,
where λ is the free-space wavelength corresponding to a frequency of 36 MHz.
of the reduced-order objective function. The true medium parameters of the object
are easily recovered by inspecting this figure. However, just as in the previous set
of experiments, we do observe a number of false minima. To see if the false min-
ima can be removed by including multi-frequency data (instead of using different
source-receiver setups as in the first set of experiments), we carry out two additional
scattering experiments, namely, one at a frequency of 30 MHz and one at a fre-
quency of 42 MHz. We now have scattered field data for three different frequencies
and the corresponding multi-frequency objective function (with weights w
q
= 1/3
for q = 1,2,3) is shown in Figure 5 (right). We observe that this objective function
does not have any false minima on the domain of interest.
In our third set of experiments we consider an inhomogeneous block. Specifi-
cally, the medium parameters of the outer part are ε
r;1
= 3 and σ
1
= 3.0 mS/m, while
the medium parameters of the inner part are given by ε
r;2
= 5 and σ
2
= 5.0 mS/m.
Furthermore, the area of the inner block is 50 % of the total area of the block and we
use the same three frequencies as in the previous experiment. For a block with a side
length d = λ /4 we then obtain the objective function as shown in Figure 6 (left). In
this figure the plus signs indicate the true medium parameters of the inner and outer
14

A Model-Order Reduction Approach to Parametric Electromagnetic Inversion
Fig. 4 An inhomogeneous
square block with a side
length d. The electric line
source (black triangle) and the
receiver (white triangle) are
located symmetrically above
the object. The background
medium is vacuum.
Relative permittivity
Conductivity
1 2 3 4 5 6
0
1
2
3
4
5
6
7
8
9
10
x 10
−3
−12
−10
−8
−6
−4
−2
0
Relative permittivity
Conductivity
1 2 3 4 5 6
0
1
2
3
4
5
6
7
8
9
10
x 10
−3
−12
−10
−8
−6
−4
−2
0
Fig. 5 Base 10 logarithm of the single-frequency (left) and multi-frequency (right) objective func-
tion on the domain of interest. The object is homogeneous and has a side length d = λ , where λ
is the free-space wavelength corresponding to a frequency of 36 MHz. The other two frequencies
used in the multi-frequency case are f = 30 MHz and f = 42 MHz. The plus sign indicates the
relative permittivity and conductivity values of the object.
part of the object. We observe that the minimum of the objective function is located
somewhere in between the medium parameter values of the inner and outer part of
the object. This can be expected, given the true medium parameters of the object.
However, if we take a larger block with d = λ we obtain the objective function as
shown in Figure 6 (right). The effective medium parameters obtained by inspect-
ing this objective function are smaller than the smallest medium parameters of the
object itself. This is a surprising result and a common phenomenon in such areas
as photonic crystals and metamaterials. These artificial media usually consist of a
periodic lattice of relatively small dielectric or metal-dielectric objects [13, 3, 14].
Analysis of infinite periodic media involves expansion of the field in terms of the
Bloch modes and leads to the band-gap phenomenon. Practically this means that
15

Rob F. Remis and Neil V. Budko
Relative permittivity
Conductivity
1 2 3 4 5 6
0
1
2
3
4
5
6
7
8
9
10
x 10
−3
−4
−3
−2
−1
0
1
2
Relative permittivity
Conductivity
1 2 3 4 5 6
0
1
2
3
4
5
6
7
8
9
10
x 10
−3
−5
−4
−3
−2
−1
0
1
Fig. 6 Base 10 logarithm of the multi-frequency objective function on the domain of interest for the
inhomogeneous block with side length d = λ/4 (left) and side length d = λ (right). The frequencies
used are f = 30 MHz, f = 36 MHz, f = 42 MHz, and λ is the free-space wavelength corresponding
to a frequency of 36 MHz. The plus signs indicate the relative permittivity and conductivity values
of the inner and outer parts of the object.
for certain frequencies, which usually form a continuous band, plane electromag-
netic waves have an imaginary wavenumber and therefore cannot propagate in such
a medium. Hence, it is convenient to describe periodic media in terms of dispersion,
i.e., dependence of the wavenumber or permittivity/permeability on the angular fre-
quency. Thus, we have two kinds of dispersion. One is due to atomic or molecular
resonances, referred to as microscopic dispersion. Another is the effective dispersion
due to periodicity and mesoscopic resonances. The latter are employed in metamate-
rials where each elementary scatterer in the periodic lattice is also a small resonator
tuned to a specific frequency band.
Although infinite periodic media are easy to analyze, finite samples of such crys-
tals cannot be studied analytically. Yet it is only natural to try to extend the notion of
the effective dispersion and effective permittivity/permeability on finite crystals as
well. This is how the so-called negative refraction materials were invented [16, 19].
To demonstrate that something like a band-gap exists even in finite photonic crystals
let us consider one depicted in Figure 7. This crystal consists of a triangular lattice
of lossless dielectric cylinders with relative permittivity ε/ε
0
= 9.61, suspended in
and surrounded by air. The cylinders have a square cross-section, 3.2 mm on the
side. The lattice period – the length of the edge of the equally-sided triangle formed
by the centers of white squares – is approximately 4.79 mm. The line source is sit-
uated in the middle, 18.6 mm down from the lower interface of the crystal. Figure 8
illustrates the changes in the field intensity within the crystal as the frequency of
the source varies. The third image corresponds to the frequency inside the photonic
band-gap as calculated for an infinite crystal. Evidently, the strong decay of the field
happens with this finite crystal as well. Hence it makes sense to try to determine the
effective permittivity of this object, and our algorithm is particularly suited for this
task. We place our receiver in the transmission regime 18.6 mm above the middle
of the upper interface. The effective scatterer is a homogeneous rectangular object
occupying the same area as the complete photonic crystal of Figure 7.
16

A Model-Order Reduction Approach to Parametric Electromagnetic Inversion
Fig. 7 Finite two-dimensional
photonic crystal with triangu-
lar lattice - relative permittiv-
ity distribution (no losses).
ε/ε
0
dist. [m]
dist. [m]
0 0.01 0.02 0.03 0.04 0.05 0.06
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
1
2
3
4
5
6
7
8
9
Intensity at 10 GHz
dist. [m]
dist. [m]
0 0.01 0.02 0.03 0.04 0.05 0.06
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
2000
4000
6000
8000
10000
12000
Intensity at 14 GHz
dist. [m]
dist. [m]
0 0.01 0.02 0.03 0.04 0.05 0.06
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
1000
2000
3000
4000
5000
6000
7000
8000
9000
10000
Intensity at 15 GHz
dist. [m]
dist. [m]
0 0.01 0.02 0.03 0.04 0.05 0.06
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
1000
2000
3000
4000
5000
6000
7000
8000
9000
Fig. 8 Field intensity inside a finite photonic crystal at different frequencies. The bottom image
demonstrates the photonic band-gap phenomenon – waves of particular frequencies cannot pene-
trate the crystal.
Since the effective permittivity is supposed to depend on the frequency in a non-
trivial way, we shall not sum over frequencies, but instead visualize the objective
function for each frequency separately. This time we shall work in terms of real and
imaginary parts of the complex permittivity. Moreover, now we are interested in a
wider domain of parameters as it is known that the effective permittivity of periodic
crystals may take non-physical values as well [15]. In the present case this means
looking at the negative values for the imaginary part of the relative permittivity, cor-
responding to media with negative losses. Mathematically, we shall be entering the
domain where the forward scattering problem does not have a unique solution. Cer-
tain values of effective permittivity with negative imaginary part are in fact eigenval-
17

Rob F. Remis and Neil V. Budko
ues of the scattering operator (matrix) [5]. This will lead to a non-invertible matrix
and thus a very high numerical value of the objective function for that particular
effective permittivity and in its immediate neighborhood. This is indeed observed in
all three images of Figure 9, where we see a tail of dark spots stretching to the right
of the zero just below the real axis. Curiously, there are also white spots, i.e. minima
Re[ε/ε
0
]
Im[ε/ε
0
]
−20 −15 −10 −5 0 5 10 15 20
−20
−15
−10
−5
0
5
10
15
20
−6
−4
−2
0
2
4
Re[ε/ε
0
]
Im[ε/ε
0
]
−20 −15 −10 −5 0 5 10 15 20
−20
−15
−10
−5
0
5
10
15
20
−16
−14
−12
−10
−8
−6
−4
−2
0
2
4
Re[ε/ε
0
]
Im[ε/ε
0
]
−20 −15 −10 −5 0 5 10 15 20
−20
−15
−10
−5
0
5
10
15
20
−10
−5
0
5
Fig. 9 Base 10 logarithm of the multi-frequency objective function on the domain of interest at 10,
14, and 15 GHz. The tail with many clustered maxima and minima corresponds to the eigenvalues
of the scattering operator. Notice the negative real part of the effective permittivity at the lower edge
of the photonic band-gap (top-right), and almost purely imaginary effective permittivity inside the
band-gap (bottom).
of the objective function, surrounding the tail of eigenvalues. This means that on
this large domain of interest, including non-physical media with negative losses, the
effective permittivity of a finite photonic is not uniquely defined. Of course, one can
exclude the lower half of the image from consideration and focus on the obvious dis-
tinct minima in the upper part only. However, in that case the effective permittivity
at lower frequencies, far outside the photonic band-gap, is not defined at all, as can
be seen from the left image of Figure 9. On the other hand, the location of the main
distinct minimum in the middle image, shows significant negative real part of the
effective permittivity as well as large effective losses (positive imaginary part). This
happens at a frequency of 14 GHz, just before the band-gap. This frequency and the
corresponding effective permittivity are important for the phenomenon of negative
refraction on photonic crystal slabs. Inside the band-gap at 15 GHz we see that the
18
A Model-Order Reduction Approach to Parametric Electromagnetic Inversion
effective permittivity is predominantly imaginary, indicating, as was expected, high
losses.
References
1. P. J. Antsaklis, A. N. Michel, Linear Systems, (Birkh
¨
auser, Boston, 2006).
2. C. Balanis, Antenna Theory - Analysis and Design, (John Wiley and Sons, New York, 1982).
3. H. Benisty, V. Berger, J.-M. Gerard, D. Maystre, A. Tchelnokov, Photonic Crystals,
(Springer, 2005).
4. N. V. Budko, R. F. Remis, Inverse Problems 20, 2004, pp. S17 – S26.
5. N. V. Budko, A. B. Samokhin, SIAM Journal on Scientific Computing 28, 2006, pp. 682 –
700.
6. W. C. Chew, J. M. Jin, E. Michielssen, J. Song, Fast and Efficient Algorithms in Computa-
tional Electromagnetics, (Artech House, Norwood, 2001).
7. V. L. Druskin, L. A. Knizhnerman, USSR Computational Mathematics and Mathematical
Physics 29, 1989, pp. 112 – 121.
8. V. Druskin, M. Zaslavsky, Inverse Problems 23, 2007, pp. 1599 – 1610.
9.
cuits and Systems 14, 1995, pp. 639 – 649.
10. A. Frommer, U. Gl
¨
assner, SIAM Journal on Scientific Computing 19, 1998, pp. 15 – 26.
11. A. Frommer, P. Maas, SIAM Journal on Scientific Computing 20, 1999, pp. 1831 – 1850.
12. G. H. Golub, Z. Strakos, Numerical Algorithms 8, 1994, pp. 241 – 268.
13. J. D. Joannopoulos, R. D. Meade, J. N. Winn, Photonic Crystals, (Princeton Univ. Press,
1995).
14. C. M. Krowne, Y. Zhang (editors), Physics of Negative Refraction and Negative Index Mate-
rials, (Springer, 2007).
15. R. Liu, T. J. Cui, D. Huang, B. Zhao, D. R. Smith, Phys. Rev. E 76(2), 2007, 026606.
16. J. B. Pendry, Phys. Rev. Lett. 85, 2000, pp. 3966 – 3969.
17. R. F. Remis, PIERS Online 2, 2006, pp. 206 – 209.
18. R. F. Remis, N. V. Budko, Proceedings ICEAA05 and EESC05, 2005, pp. 409 – 412.
19. D. R. Smith, W. J. Padilla, D. C. Vier, S. C. Nemat-Nasser, S. Schultz, Phys. Rev. Lett. 84,
2000, pp. 4184 – 4187.
20. H. A. van der Vorst, Iterative Krylov Methods for Large Linear Systems, (Cambridge Univer-
sity Press, Cambridge, 2003).
19
P. Feldman, R. W. Freund, IEEE Transactions on Computer-Aided Design of Integrated Cir-

Shifted-Laplacian Preconditioners for
Heterogeneous Helmholtz Problems
C.W. Oosterlee, C. Vuik, W.A. Mulder, and R.-E. Plessix
Abstract We present an iterative solution method for the discrete high wavenum-
ber Helmholtz equation. The basic idea of the solution method, already presented
in [18], is to develop a preconditioner which is based on a Helmholtz operator with
a complex-valued shift, for a Krylov subspace iterative method. The preconditioner,
which can be seen as a strongly damped wave equation in Fourier space, can be
approximately inverted by a multigrid method.
1 Introduction
The efficient numerical solution of the Helmholtz equation with spatially-dependent
high wavenumbers is a difficult task. The prescription of reasonable boundary con-
ditions, on a domain which is truncated for computational reasons, further compli-
cates the numerical treatment in a real-life setting. A thorough overview of the issues
regarding the numerical solution of the Helmholtz equation was presented in [56].
In a series of papers, [16, 17, 18, 47, 48, 20, 44, 57], supported by Royal Dutch
Shell and Philips via the Dutch Ministry of Economic Affairs, project BTS01044,
we have systematically developed a robust and efficient numerical solution tech-
nique for the heterogeneous high wavenumber Helmholtz equation. We have sub-
sequently looked into the method’s performance for spatially-dependent wavenum-
C.W. Oosterlee
CWI, Center for Mathematics and Computer Science, Amsterdam, and Delft University of Tech-
nology, Delft, the Netherlands, e-mail: c.w.oosterlee@cwi.nl
C.Vuik
Delft University of Technology, Delft, e-mail: c.vuik@tudelft.nl
W.A. Mulder
Shell International Exploration and Production, Rijswijk, NL e-mail: Wim.Mulder@shell.com
R-E Plessix
Shell International Exploration and Production, NL, e-mail: ReneEdouard.Plessix@shell.com
Lecture Notes in Computational Science and Engineering 71,
21
DOI 10.1007/978-3-642-03344-5_2,
B. Koren and C. Vuik (eds.), Advanced Computational Methods in Science and Engineering,
© Springer-Verlag Berlin Heidelberg 2010
C.W. Oosterlee, C. Vuik, W.A. Mulder, and R.-E. Plessix
bers, for high wavenumber problems, for the so-called absorbing boundary layer
boundary conditions, for fourth-order discretizations, for 2D and 3D applications,
academic and industrial applications. Former PhD student Yogi Erlangga, one of the
driving forces behind this series of papers, has published an overview article on the
topic, see [19], and a theoretical analysis has been presented in [20].
In [18], a preconditioned Bi-CGSTAB method has been introduced, in which the
preconditioner is based on a second Helmholtz equation with an imaginary shift.
This preconditioner is the basis of our work. It appears as a member of the family
of shifted Laplacian operators, introduced in [34]. An interesting aspect is that its
inverse can be efficiently approximated by means of a multigrid iteration, which is
somewhat surprising as the original Helmholtz equation cannot be solved efficiently
with off-the-shelf multigrid solvers. The particular preconditioner presented can be
viewed as a generalization of the work by Bayliss, Goldstein, and Turkel [4] from
the 1980s, where the Laplacian was proposed as a preconditioner for Helmholtz
problems.
The idea of preconditioning the indefinite operator with a shifted Laplacian has
now been considered also at other places in the research community. In [55] for ex-
ample, the idea is highlighted. Further, a Finnish group at Jyv
¨
askyl
¨
a has adopted the
approach for their Helmholtz applications in [25, 26, 28, 1]. The preconditioner is
also discussed and considered, for other Helmholtz applications in [12, 45, 7], and
in different research areas that need to deal with indefinite problems, like electro-
magnetics or optics, in [6, 22, 59, 36, 42].
As an example of the solver, we discuss in this paper a version of the precondi-
tioner for a fourth-order 2D finite-difference discretization of the Helmholtz oper-
ator. In the multigrid preconditioner we replace the point-wise Jacobi smoother,
from [18], by a variant of the incomplete lower-upper factorization smoother,
ILU(0). Furthermore, we show the performance of a prolongation scheme that orig-
inates from algebraic multigrid (AMG) [49]. We show that these enhancements to
the iterative solver, proposed in [57], can reduce both the number of iterations and
the total CPU time needed for convergence. Moreover, we aim to reduce the size
of the imaginary shift parameter in the shifted Laplacian preconditioner, compared
to the choice in [18], so that an even faster solution method is obtained. A fourth-
order Helmholtz discretization enables us to use fewer grid points per wavelength
compared to a second-order discretization.
Finally, the overall solution method with these algorithmic improvements is not
limited to structured Cartesian grids, as it can be set up fully algebraically (a similar
goal has been pursued in [1]). Although our method extends to solving problems on
unstructured grids, we focus here on heterogeneous Helmholtz problems on Carte-
sian grids. We focus on the two-dimensional case; however, all of the method’s
ingredients can be easily generalized to three dimensions. Previously obtained 3D
Helmholtz results, with the shifted Laplacian multigrid preconditioner, with a point-
wise smoother, can be found in [48] (academic test problems) and [44] (industrial
test problems).
This article is set up as follows. In Section 2, we discuss the Helmholtz equation,
its field of application, and the discrete finite-difference formulations of second-
22
