Загиров Н.Н. Теория обработки металлов давлением
Подождите немного. Документ загружается.

61
а б
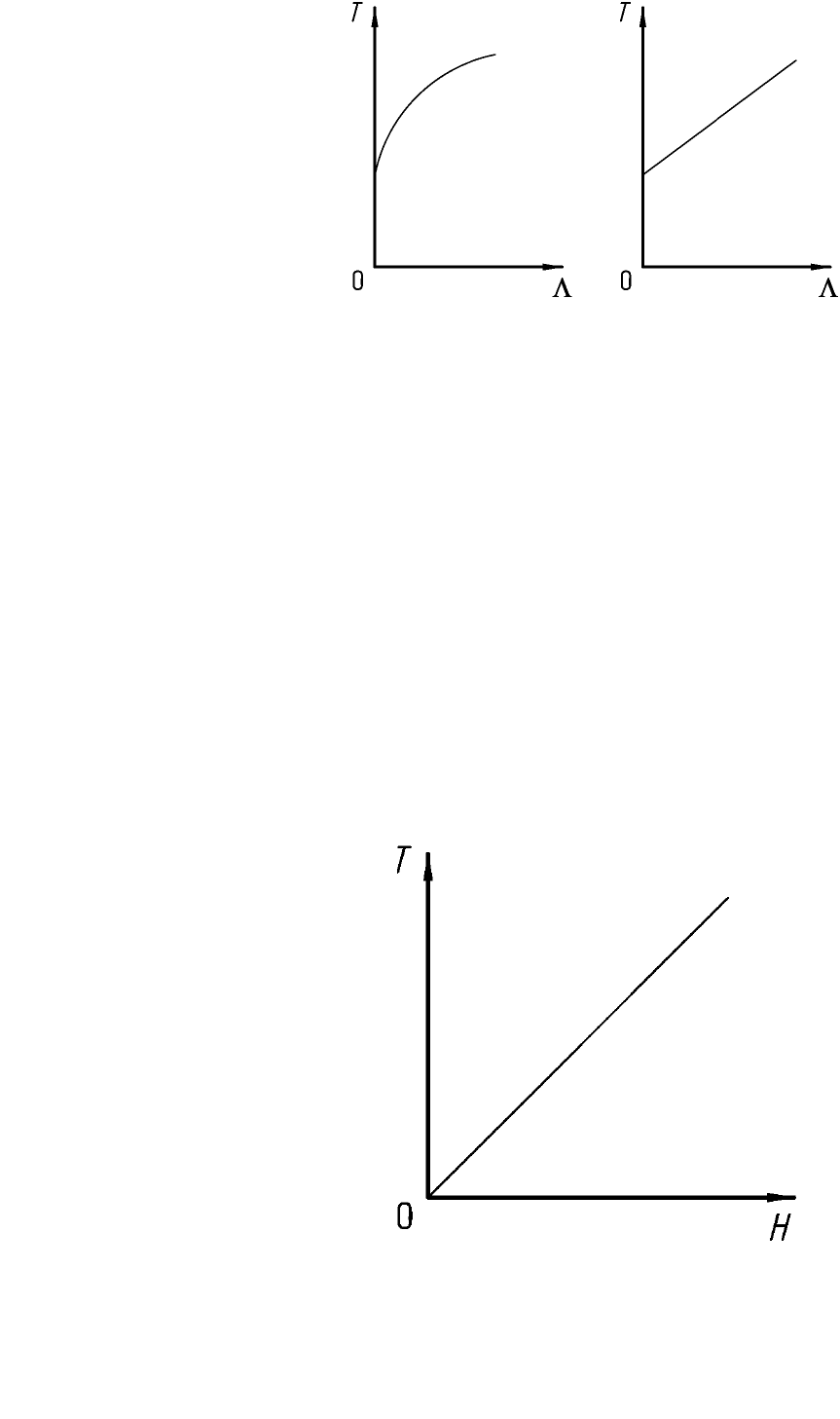
Рис. 12.2. Зависимость, отражающая модель жестко-пластичной среды
со степенным (а) и линейным (б) деформационным упрочнением
В описанных моделях сред скорость деформации не учитывают.
3. Идеальная линейно-вязкая среда (рис. 12.3) начинает деформироваться при
любом напряжении, отличном от нуля. Интенсивность касательных
напряжений пропорциональна скорости деформации такой среды, изменения
объема не происходит. Уравнение состояния идеальной линейно-вязкой
среды имеет вид:
Т = µ ⋅ Н,
где µ – коэффициент вязкости,
Рис. 12.3. Зависимость, отражающая модель линейно-вязкой среды
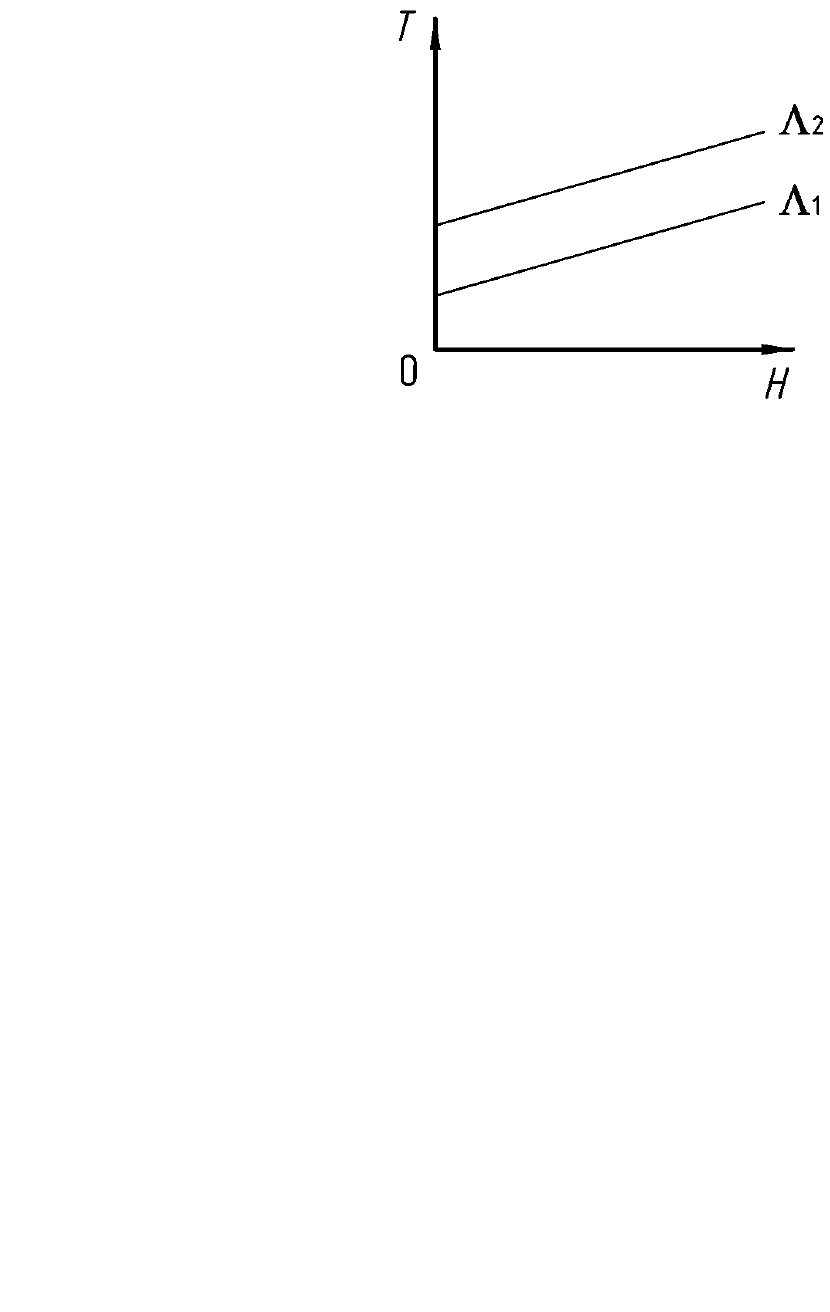
62
4. Для расчета, как усилий, так и формоизменения при горячей обработке
давлением используют модель вязко-пластической среды (рис. 12.4), для
которой характерно наличие существенной объемной сжимаемости.
Рис. 12.4. Зависимость, отражающая модель вязко-пластичной среды
Остаточное формоизменение появляется при Т = τ
S
, далее интенсивность
касательных напряжений будет зависеть от функции развития степени
деформации сдвига во времени λ = λ(t). Применительно к линейному
напряженному состоянию при растяжении уравнение состояния записывают
в виде:
Т = τ
S
+ µH.
Контрольные вопросы
1. Для чего необходимы физические уравнения связи напряженного и
деформированного состояний?
2. В каких случаях деформации может быть принята гипотеза об
изотропности?
3. Будут ли совпадать направления главных нормальных напряжений с
направлениями главных скоростей относительных удлинений?
4. Сформулируйте гипотезу о пропорциональности девиаторов напряжения и
скоростей деформации?
5. Сформулируйте (запишите) уравнения связи компонент тензора
напряжений и тензора скоростей деформации.

63
6. Дайте характеристику гипотезы о единой кривой.
7. Перечислите основные реологические модели. Какие свойства реального
металла они изображают?
8. Нарисуйте реологические кривые простых сред и запишите их уравнения
состояния при линейном напряженном состоянии.
9. Как моделируется деформационное упрочнение пластического тела?
10.Какие элементы определяют неоднозначность связи между напряжениями
и деформациями в реологических моделях?
ЛЕКЦИЯ 13
ПОЛНАЯ СИСТЕМА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
ТЕОРИИ ПЛАСТИЧНОСТИ И ОСНОВНЫЕ УПРОЩЕНИЯ,
ИСПОЛЬЗУЕМЫЕ ПРИ РЕШЕНИИ ЗАДАЧ
План лекции:
1. Полная система дифференциальных уравнений.
2. Граничные условия. Начальные условия.
3. Упрощения системы уравнений теории пластичности.
4. Изотермическая деформация.
5. Несжимаемость материала.
6. Течение без массовых сил.
7. Плоское деформированное состояние.
8. Плоское напряженное состояние.
9. Идеальная пластичность.
10. Вид уравнений в цилиндрической системе координат.
11. Примеры решения задач.
Сведем в замкнутую или полную систему дифференциальные
уравнения теории пластичности, решение которых должно дать
термомеханические переменные в каждой точке обрабатываемого тела в
любой момент его деформации. Система может иметь решение только при
соответствующем задании начальных и граничных условий, о чем будет
сказано далее.
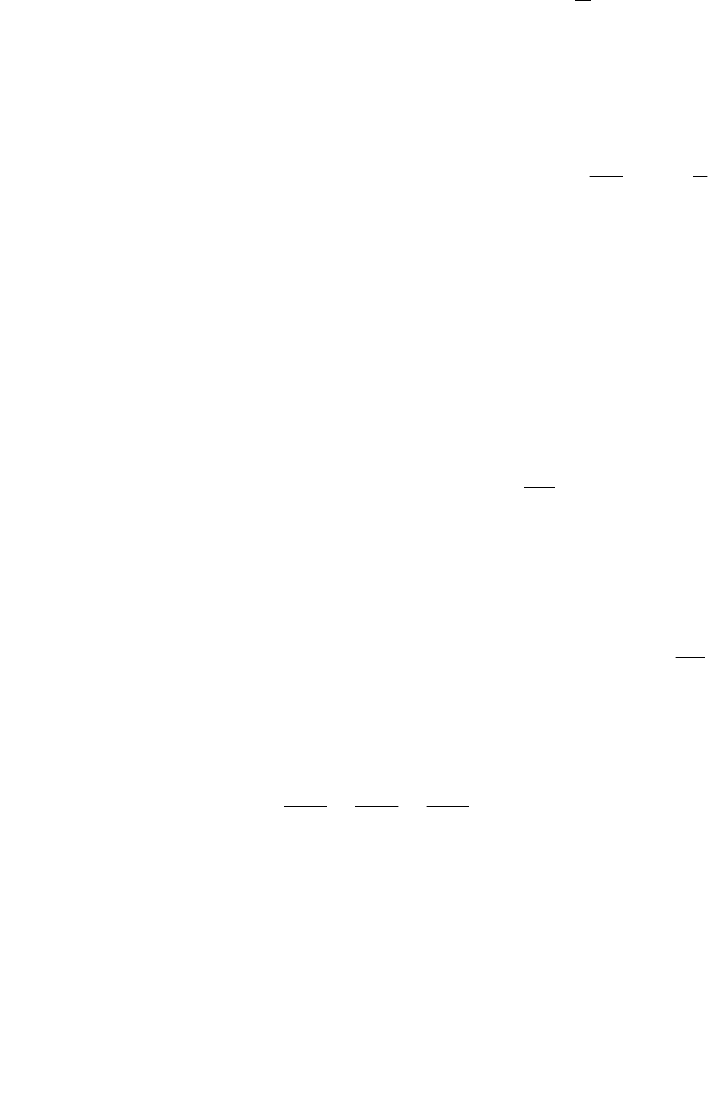
64
Полной или замкнутой системой уравнений теории пластичности
(число уравнений и неизвестных функций одинаково) называют систему
дифференциальных уравнений, объединяющую:
уравнения движения
σ
ij,j
+ ρ
gi
= ρ
ωi
; (13.1)
кинематическое уравнение
)(
2
1
i,jj,iij
υ+υ=ξ ; (13.2)
физические уравнения связи напряженного и деформированного состояний
)
3
1
(
2
ijijijij
H
T
ξδ−ξ=σδ−σ
; (13.3)
уравнение, отражающее физическую природу деформируемого материала
σ = σ(ξ); (13.4)
уравнение неразрывности
0
d
d
=ρυ+
j,i
t
S
; (13.5)
уравнение теплопроводности, имеющие в общем случае вид
t
cTH
d
d
θ
ρ=σξ++θ∆λ ; (13.6)
где λ – коэффициент теплопроводности;
2
2
2
2
2
2
zyx ∂
∂
+
∂
∂
+
∂
∂
=∆
– дифференциальный оператор Лапласа;
θ – температура материальной частицы деформируемого тела;
с – удельная массовая теплоемкость.

65
Уравнения траектории движения частицы
t
x
x
d
d
=υ ;
t
y
y
d
d
=υ ;
t
z
z
d
d
=υ . (13.7)
При решении системы уравнений теории пластичности необходимо
использовать формализованные физические условия, возникающие в
процессе деформации на поверхности (границе) тела, выраженные в
математическом виде и получившие название граничных условий. Для
получения частного решения системы уравнений должны быть заданы,
помимо граничных, еще начальные условия, т.е. значения искомых
механических переменных в каждой точке деформируемого тела в
начальный момент времени.
В связи с математическими трудностями решения краевой задачи
теории пластичности оправданы поиски упрощающих допущений, которые
бы не находились в большом противоречии с физикой конкретного
изучаемого пластического течения, но в то же время облегчали бы
вычисления. К числу таких допущений относятся предположение об
идеальной пластичности, об изотермичности течения материала, о его
несжимаемости, о достаточно медленном течении без массовых сил, о
плоских деформированном и напряженном состоянии.
Рассмотрим идеализированные процессы деформации, к которым
сводятся реальные процессы обработки металлов давлением.
1. Изотермическая деформация.
Течение металла называют изотермическим, если температура во всех
точках деформируемого тела остается постоянной в любой момент времени,
т.е. выполняется условие
θ = const.
Дифференциальное уравнение теплопроводности (13.6) отпадает.
Функция Т = Т(Н) не зависит от θ, что упрощает уравнение связи (13.3).
В реальных условиях процесс будет близок к изотермическому, если в
ходе пластической деформации тепло выделяется незначительно, а процессы
теплообмена с крутящей средой отсутствуют. Кроме того, холодную
деформацию в диапазонах присущих ей температур, можно считать как
изотермическую деформацию.

66
2. Несжимаемость материала.
Предполагается, что материал, подвергающийся пластической
деформации, несжимаем, т.е. объем тела в ходе деформирования остается
постоянным V = const, а, следовательно, остается постоянной и плотность ρ.
Уравнение неразрывности (13.5) отпадает, и возникает условие
несжимаемости
υ
i,j
= 0.
Его используют также вместо одного из уравнений связи σ = σ(ξ) и при
решении дифференциальных уравнений движения (13.1).
3. Течение без массовых сил.
Процессы ОМД являются достаточно медленными, т.е. плотность
массовых сил инерции ρ
ω
i
мала и ими можно пренебречь. Обычно мала по
сравнению с силами деформации и плотность других массовых сил ρ
gi
,
например, сил тяжести.
Если течение достаточно медленное и без массовых сил, то
дифференциальные уравнения движения (13.1) несколько упрощают и
получают дифференциальные уравнения равновесия:
σ
ij,j
= 0.
Предположение о медленном течении может дать существенную
ошибку при изучении высокоскоростных процессов ОМД: импульсного
деформирования, штамповки взрывом и т.д.
4. Плоское деформированное состояние.
Оно характеризуется тем, что движение частиц деформируемого тела
осуществляется в параллельных плоскостях и не меняется при переходе от
одной плоскости к другой.
Если предположить, что перемещение частиц тела осуществляется в
плоскостях, параллельных координатной плоскости x0y, то получим:
υ
x
= υ
x
(x, y); υ
y
= υ
y
(x, y); υ
z
= 0.
67
Из определения плоского деформированного состояния и формул (13.2)
имеем:
ξ
xz
= ξ
yz
= ξ
zz
= 0, (13.8)
тогда тензор скоростей деформации
ξξ
ξξ
=
ξ
000
0
0
yyyx
xyxx
T .
При условии (13.8) произойдут изменения и в физических уравнениях
связи (13.3). В частности, напряжение σ
xz
, определяемое по формуле
xzxz
H
T
ξ=σ
2
,
Будет равняться нулю, также как и σ
yz
. Напряжение σ
zz
, которое
определяется по формуле:
)(
H
T
zzzz
ξ−ξ=σ−σ
3
12
,
вследствие того, что ξ = ξ
xx
+ ξ
yy
, будет отлично от нуля.
Тензор напряжения примет вид
σ
σσ
σσ
=
σ
zz
yyyx
xyxx
T
00
0
0
т.е. при плоской деформации имеет место объемное напряженное состояние.
Уравнение равновесия примет вид:
0=
∂
σ
∂
+
∂
σ∂
yx
xy
xx
;
0=
∂
σ
∂
+
∂
σ
∂
yx
yyyx
.
68
Для несжимаемого материала ξ
xx
= – ξ
yy
, тогда
0
3
12
=ξ−ξ=σ−σ )(
H
T
zzzz
и, следовательно,
2
yyxx
zz
σ
+
σ
=σ=σ .
Интенсивность касательных напряжений
2
2
4
xy
yyxx
)(
T σ+
σ−σ
= .
Интенсивность скоростей деформации сдвига
22
2
xyxx
H ξ+ξ=
.
Деформированное состояние, близкое к плоской деформации,
возникает при прокатке листа, осадке и штамповке тел удлиненной формы,
волочении тонкостенных труб на оправке.
5. Плоское напряженное состояние.
Оно характеризуется тем, что напряжение, отличное от нуля, действует
в параллельных плоскостях и не меняется при переходе от одной плоскости к
другой.
Плоское напряженное состояние реализуется, например, в процессе
двустороннего растяжения плоской пластины, поскольку
σ
xz
= σ
yz
= σ
zz
= 0. (13.9)

69
При этом деформированное состояние будет объемным и описывается
тензором скоростей деформации
ξ
ξξ
ξξ
=
ξ
zz
yyyx
xyxx
T
00
0
0
.
Дифференциальные уравнения равновесия для плоского напряженного
состояния те же, что и для плоского деформированного состояния.
Условие пластичности запишется в виде
( )
[
]
Sxyxxyyyyxx
τ=σ+σ+σ+σ−σ
222
2
6
1
.
Интенсивность скоростей деформации сдвига
222
2
xyyyyyxxxx
H ξ+ξ+ξξ+ξ=
.
Примерами процессов ОМД, в которых напряженное состояние будет
близким к плоскому, являются операции листовой штамповки, волочения
труб без оправки.
6. Идеальная пластичность.
Материал называют идеально пластичным, если во время
деформирования остается постоянной величина Т, т. е. по мере изменения Н
или по мере накопления Λ
T = const.
В природе такого материала не существует. Однако известно, что
упругодеформируемый материал по мере роста напряжений довольно резко
переходит из упругого состояния в пластическое. При этом ряд материалов
обнаруживают площадку текучести: по мере развития пластической
деформации некоторое время упрочнение материала не наступает. Переход
материалов в пластическое состояние характеризуется некоторым
напряженным состоянием, интенсивность касательных напряжений для
которого T = const.

70
В общем случае условие идеальной пластичности выражается
известными формулами:
3
S
T
σ
=
, или T = τ
S
, (13.10)
где σ
S
, τ
S
, – физические характеристики реальных материалов,
подвергающихся деформации.
Для плоской деформации условие идеальной пластичности
Sxy
yyxx
T τ=σ+
σ−σ
=
2
2
4
)(
.
Если оси x и y – главные (σ
xy
= 0), то условие пластичности
преобразуется к виду
σ
11
- σ
33
= 2τ
S
≈ 1,15σ
S
.
В некоторых случаях решение краевой задачи теории пластичности
осуществляется проще, если воспользоваться не декартовой, а
криволинейной системой координат.
Рассмотрим систему уравнений теории пластичности в
цилиндрической системе координат (r, ϕ, z). Для нее можно использовать те
же индексы i, j, однако в данном случае
i, j = r, ϕ, z.
Дифференциальные уравнения движения запишутся в виде
rr
zz
rz
r
rr
g
rzrr
ρω=ρ+
σ
−
σ
+
∂
σ∂
+
ϕ∂
σ
∂
+
∂
σ∂
ϕϕϕ
1
;
ϕϕ
ϕϕϕϕϕ
ρω=ρ+
σ
+
∂
σ
∂
+
ϕ∂
σ
∂
+
∂
σ
∂
g
rzrr
zzr
2
1
; (13.11)
zz
zzzz
z
zr
g
rzrr
ρω=ρ+
σ
+
∂
σ∂
+
ϕ∂
σ
∂
+
∂
σ∂
ϕ
1
;
