Абельсон Х., Сассман Д.Д. Структура и интерпретация компьютерных программ

Подождите немного. Документ загружается.

4.1. Метациклический интерпретатор

351

Представление процедур

Работая с примитивами, мы предполагаем, что у нас есть следующие процедуры:

• (apply-primitive-procedure hпроцедураi hаргументыi)

применяет данную элементарную процедуру к значениям аргументов из списка

hаргументыi и возвращает результат вызова.

• (primitive-procedure? hпроцедураi)

проверяет, является ли hпроцедураi элементарной.

Эти механизмы работы с элементарными процедурами подробнее описаны в разде-

ле 4.1.4.

Составная процедура стр оится из параметров, т

ела процедуры и окружения при по-

мощи конструктора make-procedure:

(define (make-procedure parameters body env)

(list ’procedure parameters body env))

(define (compound-procedure? p)

(tagged-list? p ’procedure))

(define (procedure-parameters p) (cadr p))

(define (procedure-body p) (caddr p))

(define (procedure-environment p) (cadddr p))

Действия над окружениями

Интерпретатору нужно иметь несколько операций, действующих над окружениями.

Как объясняется в разделе 3.2, окружение представляет собой последовательность кад-

ров, а каждый кадр является таблицей связываний, соотносящих переменные с их зна-

чениями. Для работы с окружениями мы используем следующие операции :

• (lookup-variable-value hпеременнаяi hокружениеi) возвращает значе-

ние, связанное с символом hпеременнаяi в hокруженииi, либо сообщает об ошибке,

если переменная не связана.

• (extend-environment hпеременныеi hзначенияi hисх-окрi) возвращает

новое окружение, состоящее из нового кадра, в котором символы из списка hпеременныеi

связаны с соответствующими элементами списка hзначенияi, а объемлющим окружени-

ем является окружение hисх-окрi.

• (define-variable! hпеременнаяi hзначениеi hокружениеi) добавляет к

первому кадру hокруженияi новое связывание, которое сопоставляет hпеременнойi

hзначениеi.

• (set-variable-value! hпеременнаяi hзначениеi hокружениеi) измен яет

связывание hпеременнойi в hокруженииi так, что в дальнейшем ей будет соответствовать

hзначениеi, либо сообщает об ошибке, если пер еменная не связана.

352

Глава 4. Метаязыковая абстракция

Чтобы реализовать все эти операции, мы представляем окружение в виде списка

кадров. Объемлющее окружение живет в cdr этого списка. Пустое окружение — это

просто пустой список.

(define (enclosing-environment env) (cdr env))

(define (first-frame env) (car env))

(define the-empty-environment ’())

Каждый кадр в окружении представляется в виде пары списков: список переменных,

связанных в кадре, и список значений

(define (make-frame variables values)

(cons variables values))

(define (frame-variables frame) (car frame))

(define (frame-values frame) (cdr frame))

(define (add-binding-to-frame! var val frame)

(set-car! frame (cons var (car frame)))

(set-cdr! frame (cons val (cdr frame))))

Чтобы расширить окружен ие новым кадр ом, который связывает переменные со значе-

ниями, мы порождаем кадр, который состоит из списка перемен ных и списка значений,

и присоединяем его к окружению. Если количество переменных и количество значений

не совпадают, сообщаем об ошибке.

(define (extend-environment vars vals base-env)

(if (= (length vars) (length vals))

(cons (make-frame vars vals) base-env)

(if (< (length vars) (length vals))

(error "Получено слишком много аргументов" vars vals)

(error "Получено слишком мало аргументов" vars vals))))

Чтобы найти переменную в окружении, мы просматриваем список переменных в пер-

вом кадре. Если находим нужную переменную, то возвращаем соответствующий элемент

списк а значений. Если мы не находим переменную в текущем кадре, то ищем в объем-

лющем окружении, и так далее. Если мы добираемся до пустого окружения, нужно

сообщить об ошибке «неопределенная переменная».

(define (lookup-variable-value var env)

(define (env-loop env)

(define (scan vars vals)

(cond ((null? vars)

(env-loop (enclosing-environment env)))

В нижеследующем коде кадры не являются настоящей абстракцией данных: set-variable-value! и

define-variable! явным образом изменяют значения в кадре при помощи set-car!. Назначение процедур

работы с кадрами — сделать код операций над окружениями простым для чтения.

4.1. Метациклический интерпретатор

353

((eq? var (car vars))

(car vals))

(else (scan (cdr vars) (cdr vals)))))

(if (eq? env the-empty-environment)

(error "Несвязанная переменная" var)

(let ((frame (first-frame env)))

(scan (frame-variables frame)

(frame-values frame)))))

(env-loop env))

Чтобы присвоить перемен ной новое значение в указанном окружении, мы ищем пере-

менную, точно так же, как в lookup-variable-value, и изменяем соответс твующее

значение, когда его находим.

(define (set-variable-value! var val env)

(define (env-loop env)

(define (scan vars vals)

(cond ((null? vars)

(env-loop (enclosing-environment env)))

((eq? var (car vars))

(set-car! vals val))

(else (scan (cdr vars) (cdr vals)))))

(if (eq? env the-empty-environment)

(error "Несвязанная переменная -- SET!" var)

(let ((frame (first-frame env)))

(scan (frame-variables frame)

(frame-values frame)))))

(env-loop env))

Чтобы определить переменную, мы просматриваем первый кадр в поисках связывания

для нее, и изменяем связывание, если его удается найти (так же, как в set-variable-

value!). Если связывания не существует, мы присоединяем его к первому кадру.

(define (define-variable! var val env)

(let ((frame (first-frame env)))

(define (scan vars vals)

(cond ((null? vars)

(add-binding-to-frame! var val frame))

((eq? var (car vars))

(set-car! vals val))

(else (scan (cdr vars) (cdr vals)))))

(scan (frame-variables frame)

(frame-values frame))))

Описанный здесь метод — только один из многих способов представления окруже-

ний. Поскольку мы при помощи абстракции данных отделили конкретную реализацию

от остальных частей интерпретатора, при желании мы можем сменить представление

окружений. (См. упражнение 4.11.) В Лисп-системе промышленного каче ства быстро-

та операци й над окружениями — особенно обращения к переменной — очень сильно

влияет на общую производительность. Представлен ие, описанное здесь, при всей своей

354

Глава 4. Метаязыковая абстракция

концептуальной простоте неэфф ективно и, скорее всего, его не стали бы использовать в

рабочей системе

Упражнение 4.11.

Вместо того, чтобы представлять кадр в виде списка списков, его можно представить как список

связываний, где каждое связывание является парой из имени и значения. Перепишите операции с

окружениями в соответствии с этим альтернативным представлением.

Упражнение 4.12.

Процедуры set-variable-value!, define-variable! и lookup-variable-value можно

выразить посредством более абстрактных процедур для просмотра структуры окружений. Опреде-

лите абстракции, ко торые фиксируют общую схему поведения, и с их помощью перепишите эти

три процедуры.

Упражнение 4.13.

Scheme позволяет создавать новые связывания через define, но не дает никакого способа из-

бавиться от связывания. Реализуйте в интерпретаторе особую форму make-unbound!, которая

изымает связывание данного символа из окружения, в котором make-unbound! выполняется.

Задача определена не до конца. Например, нужно ли удалять связывания в других кадрах, кроме

первого? Дополните спецификацию и объясните свой выбор вариантов.

4.1.4. Выполнение интерпретатора как программы

Написав интерпретатор, мы получаем в руки опис ание (выраженное на Лиспе) про-

цесса вычисления лисповских выражений. Одно из преимуществ наличия описания в

виде программы в том, что эту программу можно запустить. У нас внутри Лиспа есть

работающая модель того, как сам Лисп вычисл яет выражения. Она может служить сре-

дой для экспериментов с правилами вычисления, и дальше в этой главе мы такими

экспериментами и займемся.

Программа-вычислитель в конце кон цов сводит выражен ия к применению элемен-

тарных процедур. Следовательно, единственное, что нам требуется для запуска интер-

претатора, — создать механизм, который обращается к нижележащей Лисп-системе и

моделирует вызовы элементарных процедур.

Нам нужно иметь связывание для каждого имени элементарной процедуры, чтобы,

когда eval выполняет вызов прими тива, у него был объект, который можно передать в

apply. Поэтому мы выстраиваем глобальное окружение, связывающее особые объекты

с и менами элементарных процедур, которые могут появляться в вычисляемых нами вы-

ражениях. Кроме того, глобальное окружение включает связывания для символов true

и false, так что их можно использовать как переменные в вычисляемых выражениях.

(define (setup-environment)

(let ((initial-env

Недостаток этого представления (как и варианта из упражнения 4.11) состоит в том, что вычислителю

может понадобиться просматривать слишком много кадров, чтобы найти связывание конкретной переменной.

(Такой подход называется глубокое связыв ание (deep binding).) Один из способов избежать такой потери

производительности — использовать стратегию под названием лексическая адресация (lexical addressing),

которая обсуждается в разделе 5.5.6.

4.1. Метациклический интерпретатор

355

(extend-environment (primitive-procedure-names)

(primitive-procedure-objects)

the-empty-environment)))

(define-variable! ’true true initial-env)

(define-variable! ’false false initial-env)

initial-env))

(define the-global-environment (setup-environment))

Как именно мы представляем объекты-элементарные процедуры, не имеет значения.

Требуется только, чтобы их можно было распознавать и применять, вызывая процедуры

primitive-procedure? и apply-primitive-procedure. Мы решили представ-

лять примитивы в виде списка, начинающегося с символа primitive и содержащего

процедуру нижележащего Лиспа, которая реализует данный примитив.

(define (primitive-procedure? proc)

(tagged-list? proc ’primitive))

(define (primitive-implementation proc) (cadr proc))

Setup-environment получит имена и реализации элементарных процедур из спис-

ка

(define primitive-procedures

(list (list ’car car)

(list ’cdr cdr)

(list ’cons cons)

(list ’null? null?)

другие примитивы

))

(define (primitive-procedure-names)

(map car

primitive-procedures))

(define (primitive-procedure-objects)

(map (lambda (proc) (list ’primitive (cadr proc)))

primitive-procedures))

Чтобы вызвать элементарную процедуру, м ы просто применяем процедуру-

реализацию к аргументам, используя нижележащую Лисп-систему

Любую процедуру, определенную в нижележащем Лиспе, можно использовать как примитив для метацик-

лического интерпретатора. Имя примитива, установленного в интерпретаторе, не обязательно должно совпадать

с именем его реализации в нижележащем Лиспе; здесь имена одни и те же потому, что метациклический ин-

терпретатор реализует саму S cheme. Так, например, мы могли бы написать в списке primitive-procedures

что-нибудь вроде (list ’first car) или (list ’square (lambda (x) (* x x))).

Apply-in-underlying-scheme — это процедура apply, которой мы пользовались в предыдущих гла-

вах. Процедура apply метациклического интерпретатора (раздел 4.1.1) имитирует работу этого примитива.

Наличие двух процедур с одинаковым именем ведет к технической проблеме при запуске интерпретатора,

356

Глава 4. Метаязыковая абстракция

(define (apply-primitive-procedure proc args)

(apply-in-underlying-scheme

(primitive-implementation proc) args))

Для удобства работы с ме таци клическим ин терпретатором мы организуем управля-

ющий цикл (driver loop), который моделирует цикл чтения-выполнения-печати ниже-

лежащей Лисп-системы. Этот цикл печатает подсказку (prompt), считывает входное

выражение, вычисляет это выражение в глобальном окружении и распечатывает резуль-

тат. Пер ед каждым результатом мы помещаем подсказку вывода (output prompt), чтобы

отличить значение выражения от всего прочего, что может быть напечатано

(define input-prompt ";;; Ввод M-Eval:")

(define output-prompt ";;; Значение M-Eval:")

(define (driver-loop)

(prompt-for-input input-prompt)

(let ((input (read)))

(let ((output (eval input the-global-environment)))

(announce-output output-prompt)

(user-print output)))

(driver-loop))

(define (prompt-for-input string)

(newline) (newline) (display string) (newline))

(define (announce-output string)

(newline) (display string) (newline))

Мы пользуемся специальной процедурой вывода user-print, чтобы не печатать окру-

жение составных процедур, которое может быть очень длинным списком, и даже может

содержать циклы.

(define (user-print object)

(if (compound-procedure? object)

(display (list ’compound-procedure

(procedure-parameters object)

(procedure-body object)

’<procedure-env>))

(display object)))

поскольку определение apply метациклического интерпретатора загородит определение при митива. Можно

избежать этого, переименовав метациклический apply, и избавиться таким образом от конфликта с име-

нем элементарной процедуры. Мы же вместо этого приняли решение сохранить ссылку на исходный apply,

выполнив

(define apply-in-underlying-scheme apply)

прежде, чем определили apply в интерпретаторе. Теперь мы можем обращаться к исходной версии apply под

другим именем.

Элементарная процедура read ожидает ввода от пользователя и возвращает ближайшее полное выра-

жение, которое он напечатает. Например, если пользователь напечатает (+ 23 x), результатом read будет

трехэлементный список из символа +, числа 23 и си мвола x. Если пользователь введет ’x, результатом read

будет двухэлементный список из символа quote и символа x.

4.1. Метациклический интерпретатор

357

Теперь для запуска интерпретатора нам остается только проинициализировать гло-

бальное окружение и войти в управляющий цикл. Вот пример работы интерпретатора:

(define the-global-environment (setup-environment))

(driver-loop)

;;; Ввод M-Eval:

(define (append x y)

(if (null? x)

(cons (car x)

(append (cdr x) y))))

;;; Значение M-Eval:

;;; Ввод M-Eval:

(append ’(a b c) ’(d e f))

;;; Значение M-Eval:

(a b c d e f)

Упражнение 4.14.

Ева Лу Атор и Хьюго Дум экспериментируют с метациклическим интерпретатором каждый по

отдельности. Ева вводит определение map и запускает несколько тестовых программ с его ис-

пользованием. Они замечательно работают. Хьюго, со своей стороны, ввел системную версию map

как примитив метациклического интерпретатора. Когда он пы тается его выполнить, все ломается

самым ужасным образом. Объясните, почему у Хьюго map не раб отает, а у Евы работает.

4.1.5. Данные как программы

При рассмотрении программы на Лиспе, вычисляющей лисповские выражения, может

быть полезна аналогия. Одна из возможных точек зрения на значение программы состоит

в том, что программа описывает абстрактную (возможно, бесконечно большую) машину.

Рассмотрим, например, знакомую нам программу для вычисления факториалов:

(define (factorial n)

(if (= n 1)

(* (factorial (- n 1)) n)))

Можно считать эту программу описанием машины, которая содержит узлы для вычита-

ния, умножения и проверки на равенство, двухпозиционный переключатель и еще одну

факториал-машину. (Факториал-машина получается бесконечной, поскольку она содер-

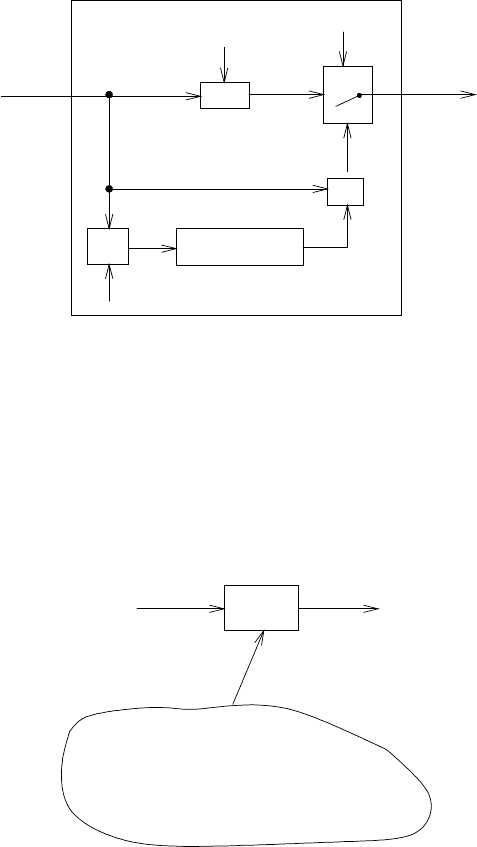
жит другую факториал-машину внутри себя.) На рисунке 4.2 изображена потоковая

диаграмма факториал-машины, которая показывает, как спаяны ее части.

Подобным образом, мы можем рассматривать вычислитель как особого рода машину,

которой подается в виде сырья описание другой машины. Обработав свои входные дан-

ные, вычислитель перестраивает себя так, чтобы моделировать описываемую машину.

358

Глава 4. Метаязыковая абстракция

factorial

720

factorial

Рис. 4.2. Программа вычисления факториала, изображенная в виде абстрактной машины.

(define (factorial n)

(if (= n 1)

(* (factorial (- n 1)) n)))

720

eval

Рис. 4.3. Вычислитель, моделирующий факториальную машину.

4.1. Метациклический интерпретатор

359

Напри мер, если мы скормим вычислителю опреде ление factorial, как показ ано на

рисун ке 4.3, он сможет считать факториалы.

С этой точки зрения, наш вычислитель-интерпретатор выглядит как универсальная

машина (universal machine). Она имитирует другие машины, представленные в виде

Лисп-программ

. Это замечательное ус тройство. Попробуйте представить себе анало-

гичный вычислитель для электрических схем. Это была бы схема, которой на вход по-

ступает сигнал, кодирующий устройство какой-то другой схемы, например, фильтра.

Восприняв этот вход, наша схема-вычислитель стала бы работать как фильтр, соответ-

ствующий описанию. Такая универсальная электрическая схема имеет почти невообра-

зимую сложность. Удивительно, что и нтерпретатор программ — сам по себе программа

довольно простая

Еще одна замечательная черта интерпретатора заключается в том, что он служит

мостом между объектами данных, которыми манипулирует язык программирования, и

самим языком. Представим себе, что работает программа интерпретатора (реализован-

ная на Лиспе), и что пользователь вводит выражения в интерпретатор и рассматривае т

результаты. С точки зрения пользователя, входное выражение вроде (* x x) является

выражением языка программирования, которое интерпретатор должен выполнить. Одна-

ко с точки зрения интерпретатора это всего лишь список (в данном случае, список из

трех символов: *, x и x), с которым нужно работать по ясно очерченным правилам.

Нас не должно смущать, что программы пользователя являются данными для интер-

претатора. На самом деле, иногда бывает удобно и гнорировать это различие и, предостав-

ляя пользовательским программам доступ к eval, давать пользователю возможность

явным образом вычислить объект данных как выражение Лиспа. Во многих диалектах

Лиспа имеется элементарная процедура eval, которая в виде аргументов берет выра-

жение и окружение, и вычисляет выражение в указанном окружении

. Таким о бразом,

То, что машины описаны на языке Лисп, несущественно. Если дать нашему интерпретатору программу на

Лиспе, которая ведет себя как вычислитель для какого-нибудь другого языка, скажем, Си, то вычислитель для

Лиспа будет имитировать вычислитель для Си, который, в свою очередь, способен сымитировать любую маши-

ну, описанную в виде программы на Си. Подобн ым образом, написание интерпретатора Л испа на Си порождает

программу на Си, способную выполнить любую программу на Лиспе. Главная идея здесь состоит в том, что

любой вычислитель способен имитировать любой другой. Таким образом, понятие «того, что в принципе можно

вычислить» (если не принимать во внимание практические вопросы времени и памяти, потребной для вычис-

ления), независимо от языка компьютера и выражает глубинное понятие вычислимости (computability). Это

впервые было ясно показано Аланом М. Тьюрингом (1912-1954) , чья статья 1936 года заложила основы теоре-

тической информатики. В этой статье Тьюринг представил простую модель вычислений, — теперь известную

как машина Тьюринга (Turing machine), — и утверждал, что любой «эффективный процесс» выразим в виде

программы для такой машины. (Этот аргумент известен как тезис Чёрча-Тьюринга (Church-Turing thesis).)

Затем Тьюринг реализовал универсальную машину, т. е. машину Тьюринга, которая работает как вычислитель

для программ машин Тьюринга. При помощи этой схемы рассуждений он показал, что существуют коррекно

поставленные задачи, которые не могут быть решены машиной Тьюринга (см. упражнение 4.15), а следователь-

но не могут быть сформулированы в виде «эффективного процесса». Позднее Тьюринг внес фундаментальный

вклад и в развитие практической информатики. Например, ему принадлежит идея структурирования программ

с помощью подпрограмм общего назначения. Биографию Тьюринга можно найти в Hodges 1983.

Некоторые считают странным, что вычислитель, реализованный с помощью относительно простой проце-

дуры, способен имитировать программы, более сложные, чем он сам. Существование универсальной машины-

вычислителя — глубокое и важное свойство вычисления. Теория рекурсии (recursion theory), отрасль матема-

тической логики, занимается логическими пределами вычислимости. В прекрасной книге Дугласа Хофштадтера

«Гёдель, Эшер, Бах» (Hofstadter 1979) исследуются некоторые из этих идей.

Предупреждение: эта процедура eval — не то же самое, что процедура eval, реализованная нами в

разделе 4.1.1, потому что она работает с настоящими окружениями, а не с искусственными структурами

360

Глава 4. Метаязыковая абстракция

как

(eval ’(* 5 5) user-initial-environment)

так и

(eval (cons ’* (list 5 5)) user-initial-environment)

возвращают результат 25

Упражнение 4.15.

Если даны одноаргументная процедура p и объект a, то говоря т, что p «останавливается» на a,

если выражение (p a) возвращает значение ( а не печатает сообщение об ошибке или выполняется

вечно). Покажите, что невозможно написать процедуру halts?, которая бы точно определяла для

любой процедуры p и любого объекта a, останавливается ли p на a. Используйте следующее

рассуждение: если бы имелась такая процедура halts?, можно было бы написать следующую

программу:

(define (run-forever) (run-forever))

(define (try p)

(if (halts? p p)

(run-forever)

’halted))

Теперь рассмо трите выражение (try try) и покажите, что любое возможное завершение (о ста-

новка или вечное выполнение) нарушает требуемое поведение halts?

4.1.6. Внутренние определения

Наша модель вычислений с окружениями и метациклический интерпретатор выпол-

няют опреде ления по очереди, расширяя кадр окружения на одно определение за раз.

Это особенно удобно для диалоговой разработки программы, когда програм м исту нужно

свободно смешивать вызовы процедур с определениями новых процедур. Однако если

мы внимательно поразмыслим над внутренними определениями, с помощью которых ре-

ализуется блочная структура (введенная в разделе 1.1.8), то мы увидим, что пошаговое

расширение окружения — одно имя за другим — может оказаться не лучшим способом

определения локальных переменных.

Рассмотрим процедуру с внутренними определениями, например

окружений, которые мы построили в разделе 4.1.3. С этими настоящими окружениями пользователь не может

работать, как с обычными списками; к ним нужно обращаться через eval или другие специальные операции.

Подобным образом, элементарная процедура apply, упомянутая раньше, не то же самое, что метацикличе-

ская apply, поскольку она использует настоящие процедуры Scheme, а не объекты-процедуры, которые мы

конструировали в разделах 4.1.3 и 4.1.4.

Реализация MIT Scheme имеет процедуру eval, а также символ user-initial-environment, связан-

ный с исходным окружением, в котором вычисляются выражения.

Хотя здесь мы предположили, что halts? получает процедурный объект, заметим, что рассуждение оста-

ется в силе даже в том случае, когда на вход подается текст процедуры и ее окружение. В этом и состоит

знаменитая теорема об остановке (Halting Theorem) Тьюринга, в которой был дан первый пример невы-

числи м ой (non-computable) задачи, т. е. корректно поставленного задания, которое невозможно выполнить с

помощью вычислительной процедуры.