Абрамов С.А., Гнездилова Г.Г., Капустина Е.Н., Селюн М.И. Задачи по программированию

Подождите немного. Документ загружается.

натурального n в двоично-десятичной системе (см. предыдущую

задачу), найти натуральное n в десятичной системе.

602. Доказать, что любое натуральное число n можно

единственным способом представить с помощью некоторых целых

неотрицательных d

,…, d

в виде d

(s+1)!+ d

s-1

s!+…+ d

2!+ d

при

условии, что 0 ≤ d

≤ i+1, i=0, …, s, d

≠0.

Дано натуральное число n; найти соответствующие d

, d

s-1

, …,

603. В качестве основания позиционной системы может быть

взято отрицательное целое число. Например, можно рассмотреть

систему с основанием –10. Любое целое n единственным образом

представляется в виде суммы a

(–10)

+ a

s-1

(–10)

s-1

+…+ a

(–10)+a

, где

0 ≤ a

≤ 9, i =0, …, s. Из сказанного следует, что любое целое n

записывается в системе с основанием –10 в виде целого числа без

знака a

s-1

, …, a

Дано целое число n. Построить представление n в системе с

основанием –10, т.е. найти соответствующие a

, a

s-1

, …, a

604. Рассмотрим последовательность натуральных чисел w

, w

…, образованную по следующему закону: w

=1, w

=2, w

= w

k-1

+ w

k-2

(k=2, 3, …). Эта последовательность – сдвинутая последовательность

чисел Фибоначчи (см. задачу 144) w

, w

Последовательность w

, w

, …, – это 1, 2, 3, 5, 8, 13, 21, … Доказать,

что любое натуральное n можно единственным способом представить с

помощью некоторых неотрицательных целых b

,…, b

в виде b

+ b

t-1

+…+ b

при условии, что 0 ≤ b

≤ 1, i=0, …, t, b

≠

0. При этом две

единицы не могут стоять рядом: если b

=1, то b

i+1

=0 (i=0,…, t–2).

Дано целое неотрицательное число n; найти соответствующие

, b

t-1

, …, b

605. «Римские цифры».

а) Проверить, правильна ли запись числа римскими цифрами.

б) Записать данное число из диапазона от 1 до 1999 римскими

цифрами.

в) Перевести число, записанное римскими цифрами, в

десятичную систему.

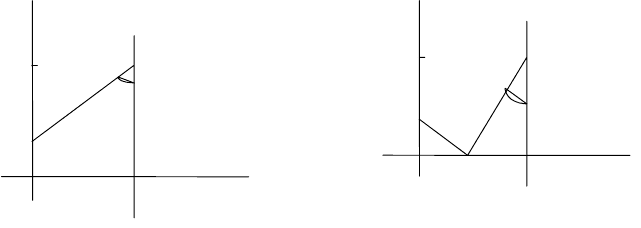
§ 17. Геометрия

606. Даны действительные положительные числа a, b, c, d.

Выяснить, можно ли построить четырехугольник с такими длинами

сторон.

607. Дано действительное число )0(

<< . Из точки (1, 1)

под углом

к прямой x=1 выпущен световой луч (рис. 29, а – 29, b).

Найти точку оси ординат, в которой луч падает на эту ось.

Если 4/

< , то луч сначала отразится по закону «угол падения равен

углу отражения» от оси абсцисс.

Рис. 29

608. Даны действительные числа x

, y

, x

, y

≠x

), которые

определяют две точки A(x

, y

) и B(x

, y

). На оси абсцисс найти такую

точку, сумма расстояний от которой до точек A и B – наименьшая для

всех точек этой оси.

609. Даны действительные числа x, y. Вычислить расстояние от

точки плоскости с координатами (x, y) до границы квадрата *) с

вершинами:

а) (–0.5, –0.5), (–0.5, 0.5), (0.5, 0.5), (0.5, –0.5);

б) (0, 0), (0, 1), (1, 1), (1, 0).

*) То есть минимум расстояний от данной точки до точек границы

квадрата.

610. Даны натуральное число n, целые числа x

, y

, x

, y

, …, x

. Известно, что точки p

, …, p

с координатами (x

, y

), (x

, y

), …, (x

) попарно различны. Пусть точка p

удалена от начала координат на

расстояние r

(i=1, …, n). Пусть R = max(r

, …, r

а) Среди точек p

, …, p

выбрать какую-нибудь одну p

, для

которой r

=R; у казать координаты выбранной точки и расстояние от

этой точки до начала координат.

б) Среди точек p

, (1 ≤i ≤n)для которых r

=R, выбрать те,

которые обладают наименьшей абсциссой. Если таких точек больше

одной, то выбрать из них точку, которая имеет наибольшую ординату.

Указать номер выбранной точки.

611. Даны действительные числа a

, …, a

. Эти числа

определяют 25 интервалов числовой оси: (a

, a

), (a

, a

), …, (a

, a

а) Имеют ли все данные интервалы общие точки? Если да, то

указать какую-нибудь из этих точек.

б) Является ли интервалом объединение данных интервалов?

Если да, то указать концы этого интервала.

в) Указать число i (1 ≤i ≤25) такое, что объединение данных

интервалов можно представить в виде i непересекающихся интервалов.

г) Имеются ли точки числовой оси, принадлежащие по крайней

мере трем каким-нибудь из данных интервалов? Если да, то указать

какую-нибудь из этих точек.

612. Даны действительные числа x

, …, x

, y

, …, y

, r

, …, r

Выяснить, есть ли на плоскости точка, принадлежащая всем кругам c

…, c

, где с

имеет центр с координатами x

, y

и радиус r

(i=1, …, 15).

613.Даны действительные числа x

, y

, x

, y

, …, x

, y

, которые

рассматриваются как координаты (x

, y

), (x

, y

), …, (x

, y

) точек на

плоскости. Выяснить, верно ли, что для каждой из этих пятнадцати

точек найдется другая, такая, что все оставшиеся тринадцать точек

лежат по одну сторону от прямой, проходящей через эти две точки.

614.Даны целые числа x

, y

, x

, y

, …, x

, y

. Выяснить, найдутся

ли среди точек с координатами (x

, y

), (x

, y

), …, (x

, y

) четыре таких,

которые являются вершинами квадрата.

615.Даны целые числа x

, y

, x

, y

, x

, y

. Известно, что точки с

координатами (x

, y

), (x

, y

), (x

, y

) являются тремя вершинами

некоторого прямоугольника. Найти координаты четвертой вершины.

616.Прямая на плоскости может быть задана уравнением

ax+by+c=0, где a и b одновременно не равны нулю. Будем

рассматривать прямые только с целыми коэффициентами a, b, c. Пусть

даны коэффициенты нескольких прямых: a

, b

, c

, a

, b

, c

, …, a

, b

a) Определить, имеются ли среди этих прямых совпадающие

или параллельные.

б) Определить, имеются ли три прямые, пересекающиеся в

одной точке.

в) Определить, находятся ли данные прямые в общем

положении. (Прямые находятся в общем положении, если все они

различны, никакие две из них не параллельны и никакие три не

пересекаются в одной точке.)

617.Окружность на плоскости может быть задана координатами

x, y ее центра и радиусом r. Пусть даны соответствующие

характеристики нескольких окружностей: x

, y

, r

, x

, y

, r

, …, x

, y

, r

а) Определить, имеются ли среди этих окружностей три

попарно пересекающиеся.

б) Найти среди этих окружностей все уединенные окружности,

т. е. такие, которые не имеют общих точек ни с одной из остальных

окружностей , не лежат целиком внутри и не заключают внутри себя

какой-либо из остальных окружностей.

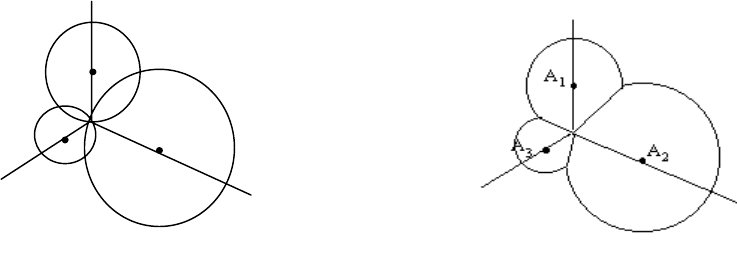
618.Рассматриваются три луча, проведенные в плоскости из

точки О. Углы между соседними лучами равны 2

/3. На лучах

выбраны точки А

, А

, и из этих точек как из центров проведены

окружности, проходящие через точку О. Считая данными расстояния

О, А

О, вычислить площадь фигуры, изображенной на рис. 30,

а. Для вычисления разбить фигуру на части так, как показано на рис.

30, б.

Рис.30