ACCA F2 Management Accounting - 2010 - Study text

Подождите немного. Документ загружается.

Chapter 4: Business mathematics and computer spreadsheets

If you plot a graph of the data relating to two variables, you should be able to see if

any visible relationship exists between them (such a graph is known as a

scattergraph or scatterchart). If a visible relationship is seen to exist, the data on the

graph can be plotted to show the ‘line of best fit’. The ‘line of best fit’ is of the form

y = a + bx (linear cost function) and indicates that a ‘possible’ linear relationship

exists between two variables.

3.2 Degrees of correlation

The following scattergraphs show the different degrees of correlation that may be

seen to exist between two variables.

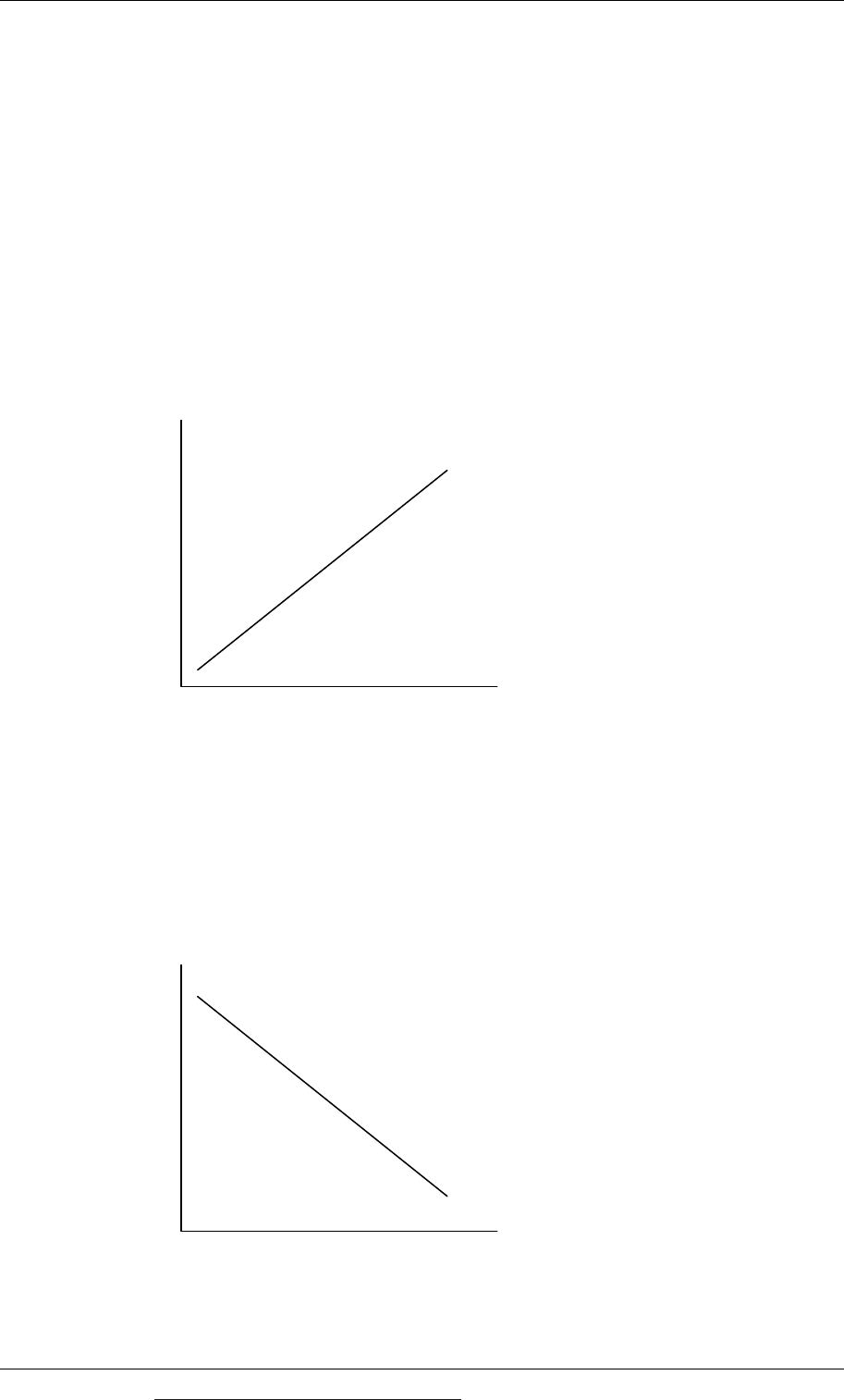
Perfect positive correlation

Perfect correlation is seen to exist when all the data points plotted lie in an exact

straight line and a linear relationship exists between the two variables.

Perfect positive correlation means that high values of are variable are associated

with high values of another variable. Alternatively, low values of one variable may

be associated with low values of another variable.

Perfect negative correlation

Paper F2: Management accounting

76 Go to www.emilewoolfpublishing.com for Q/As, Notes & Study Guides © EWP

Perfect negative correlation is seen to exist when all the data points plotted lie in an

exact straight line and that high values of one variable are associated with low

values of another variable. Alternatively, low values of one variable may be

associated with high value of another variable.

No correlation (uncorrelated)

‘Uncorrelated’ means that no correlation is seen to exist between the variables.

Positive correlation (but not perfect correlation)

Positive correlation means that there appears to be some correlation between the

values of y and x, and in general the value of y increases as the value of x increases.

However, the correlation is not perfect because all the data does not lie exactly on a

straight line on the scattergraph.

Chapter 4: Business mathematics and computer spreadsheets

Negative correlation

Negative correlation means that a relationship exists between two variables, and the

value of y declines as the value of x increases. However, the correlation is not

perfect.

As an alternative to drawing a scattergraph to see whether a visible relationship

exists between the two variables x and y, the correlation between them can be

measured by calculating a

correlation coefficient.

3.3 Correlation coefficient r

An advantage of using the regression analysis method is that the reliability of the

estimates can be assessed statistically, by calculating a correlation coefficient.

The formula for the correlation coefficient (r) will be given to you in the

examination.

r =

∑

xy –

∑

n∑x

– ∑ x

()

n ∑y

– ∑ y

()

This formula might seem difficult, but it is fairly similar to the formula for

calculating ‘b’ in the linear cost equation. The only additional value that we need to

calculate the correlation coefficient is a value for [n∑y

– (∑y)



If you look back at the previous example, you will see that the value for ∑y

has

already been calculated. In the example, there is a separate column for y

Calculate the square of each value of y in the y column and enter it in the same

row in the y

column

Then add up all the values of y

in the y

column to get

∑y

 (∑y)

is a different value. It is the square of the value for ∑y.

The value of the correlation coefficient, r, in the example in paragraph 2.3 is

therefore calculated as follows. Remember that most of the values for the formula

have been calculated in paragraph 2.3 as parts of the formula for calculating the

value of b.

Paper F2: Management accounting

78 Go to www.emilewoolfpublishing.com for Q/As, Notes & Study Guides © EWP

r =

249

(41) [6(136,185) – (903)

]

249

(41) (1,701)

249

264

= +0.94

The correlation coefficient is + 0.94.

Significance of the correlation coefficient

The value of the correlation coefficient must always be in the range – 1 to + 1.

 A value of – 1 indicates that there is perfect negative correlation between the

values for y and the values for x that have been used in the regression analysis

estimates. Perfect negative correlation means that all the values for x and y,

plotted on a graph, would lie on a straight downward-sloping line.

 A value of + 1 indicates that there is perfect positive correlation between the

values for y and the values for x that have been used in the regression analysis

estimates. Perfect positive correlation means that all the values for x and y,

plotted on a graph, would lie on a straight upward-sloping line.

 A value of r = 0 indicates no correlation at all between the values of x and y.

For cost estimation, a value for r close to + 1 would indicate that the cost estimates

are likely to be very reliable.

As a general guide, a value for r between + 0.90 and + 1 indicates good correlation

between the values of x and y, suggesting that the formula for costs can be used

with reasonable confidence for cost estimation.

If you calculate a value for r that is more than +1 or is a greater negative value than

– 1, your calculation will be wrong.

3.4 Coefficient of determination r

The square of the correlation coefficient, r

, is called the coefficient of determination.

The value of r

shows how much the variations in the value of y, in the data used to

calculate the regression analysis formula, can be explained by variations in the value

of x.

Significance of coefficient of determination

The value of the coefficient of determination must always be in the range 0 to +1.

 If the value of r is + 0.70, this means that on the basis of the data used in the

regression analysis formula, 0.49 or 49% (= 0.70

) of variations in the value of y

can be explained by variations in the value of x.

 Similarly if the value of r is – 0.80, this means that on the basis of the data used

in the regression analysis formula, 0.64 or 64% (= 0.80

) of variations in the value

of y can be explained by variations in the value of x. Since r is negative, this

means that y falls in value as the value of x increases.

In the example above, where r = + 0.94, we can say that from the data used to

produce a formula for total costs, 88.36% (0.94 × 0.94 = 0.8836) of the variations in

Chapter 4: Business mathematics and computer spreadsheets

total cost can be explained by variations in the volume of output. This would

suggest that the formula obtained for total costs is likely to be fairly reliable for

estimating future costs for any given (budgeted) volume of production.

The coefficient of correlation and the coefficient of determination can therefore be

used to give a statistical measurement to the reliability of estimates of y from a

given value for x, using a line of best fit that has been calculated by linear regression

analysis. As you might imagine, this can be a very useful item of management

information for the purpose of forecasting or planning.

Paper F2: Management accounting

80 Go to www.emilewoolfpublishing.com for Q/As, Notes & Study Guides © EWP

Spreadsheet models

 Features of a spreadsheet

 Using spreadsheets

 Applications of spreadsheets in cost and management accounting

 ‘What if’ analysis: sensitivity analysis

4 Spreadsheet models

4.1 Features of a spreadsheet

Spreadsheets are used extensively in management accounting, because they enable

accountants to make long and detailed calculations very quickly.

A spreadsheet program is a type of computer software. A spreadsheet is a table of

rows and columns. Like any table, the rows and columns can contain words, figures

or other symbols. A spreadsheet program is used to create spreadsheets.

A spreadsheet created by a spreadsheet program enables the user to prepare one or

more tables of figures. Any table of figures, no matter how complex, can be

prepared in a spreadsheet.

A blank spreadsheet is simply a huge table of rows and columns, with each row and

having a unique identity number and each column having a unique letter code (A,

B, C …AA, AB, etc). The table therefore consists of boxes or cells, and each cell can

be identified by a unique combination of column letters and row number, such as

B5, T28, AA4 and so on.

A description of the features of a spreadsheet system is given in an Appendix at the

end of this text. If you are not familiar with spreadsheets, you should read the

Appendix before continuing to read this chapter.

4.2 Using spreadsheets

A blank spreadsheet can be used to create a table of figures by entering words,

figures and formulae. Figures are entered in the appropriate cells if their values are

known. Otherwise a formula can be entered into a cell, and the spreadsheet model

will convert the formula into a numerical value. The use of formulae in spreadsheets

is the reason why they can be used to produce tables of figures so quickly. Formulae

avoid the need to make calculations ‘by hand’ with a calculator.

Example

The example below is a very simple illustration of how spreadsheets are used to

construct accounting calculations.

Chapter 4: Business mathematics and computer spreadsheets

All text in this column

Entered in the

spreadsheet file as text of

formulae

Shown in the spreadsheet

on screen or printout

Column F G

Row

Year Sales Sales

7 $

8 1 100,000

100,000

9 2 =G8*1.05

105,000

10 3 =G9*1.05

110,250

11 Total sales Years 1 -

=G8+G9+G10

315,250

12 Average annual sales

=G11/3

105,083

Column G is shown twice here. The left hand column for G shows the data as it has

been entered into the spreadsheet as formulae. The left hand column for G shows

the data that is displayed on the screen and in printouts.

The figures in the spreadsheet can be changed quickly simply by amending some of

the data in the cells. For example, if the accountant wants to change the figures so

that sales in Year 1 are $110,000 and annual sales growth in Years 2 and 3 is 4%, he

can do this by amending the number in cell G8 to 110,000 and amending cells G9

and G10 to change 1.05 to 1.04.

Example

Here is another example of a simple accounting calculation entered as text,

numbers and formulae in a spreadsheet.

Column C D

E F

Row

6 months 2

6 months Year

4 Output (units) 10,000

15,000 = D4+E4

$ $

6 Variable costs =D4*F11

=E*F11 =D6+E6

7 Fixed costs 40,000

=D7 =D7+E7

8 Total costs =D6+D7

=E6+E7 =D8+E8

10 Average cost/unit =D8/D4

=E8/E4 =F8/F4

11 Variable cost/unit

3.00

This would appear on screen as follows:

Column C D

E F

Row

6 months 2

6 months Year

4 Output (units) 10,000

15,000 25,000

$ $

6 Variable costs 30,000

45,000 75,000

7 Fixed costs 40,000

40,000 80,000

8 Total costs 70,000

85,000 155,000

10 Average cost/unit 7.00

5.67 6.20

11 Variable cost/unit

3.00

The figures can be re-calculated using different figures for output in each half of the

year, or different figures for fixed costs or the unit variable costs. All that is required

is an alteration to the number in cells D4, E4, D7 or F11.

Paper F2: Management accounting

4.3 Applications of spreadsheets in cost and management accounting

Spreadsheets can be used for many tasks in cost and management accounting,

where a large number of calculations are required. They are used to construct

mathematical ‘models’ and to carry out a large number of calculations quickly and

accurately.

Examples of applications of spreadsheets in management accounting include:

 Preparing forecasts of sales, and forecasts of profit or loss

 Cost estimation using linear regression analysis and the calculation of a

correlation coefficient and coefficient of determination

 Preparing financial plans, such as budgets

 Comparing actual results with a plan or budget (control reporting).

Each table or set of related tables in a spreadsheet is held in a single file and

accountants often carry a number of spreadsheet files on their lap top computer.

There are cost and management applications for which spreadsheets are not

suitable. These include any application involving the recording and filing of large

amounts of data. For these applications, involving the maintenance of records and

large files, other types of software are more suitable, such as:

 A cost accounting software package for keeping cost accounting records (in a

double entry ‘book-keeping’ system)

 An inventory control software package for maintaining records of inventory

 A database for maintaining and accessing other large files of data.

Graphical reproduction of spreadsheet data

Spreadsheets can be printed out and included in management reports. It is very

common in practice to find tables of figures produced in a spreadsheet to be

included as appendices in management reports.

In addition, the figures in a spreadsheet can be converted by the spreadsheet

program into graphical display format, and shown as graphs, bar charts or pie

charts. This facility can also be very useful for the preparation of management

reports.

For example, if a spreadsheet is used for linear regression analysis, it can be used to

show the line of best fit as a graph. Similarly, if a spreadsheet is used to prepare an

estimate of costs, the percentage of total costs made up by different items of cost

(direct materials, direct labour, production overheads etc) can be shown as a pie

chart or a bar chart.

Chapter 4: Business mathematics and computer spreadsheets

Applications of spreadsheets in management accounting include:

 Making forecasts, such as sales forecasts

 Preparing budgets and other financial plans

 Preparing flexible budgets for comparing actual and expected costs

 Preparing a complex income statement.

Some examples of spreadsheets are illustrated below. Don’t worry about the detail

in these examples. Cost-volume-profit analysis will be explained in a later chapter.

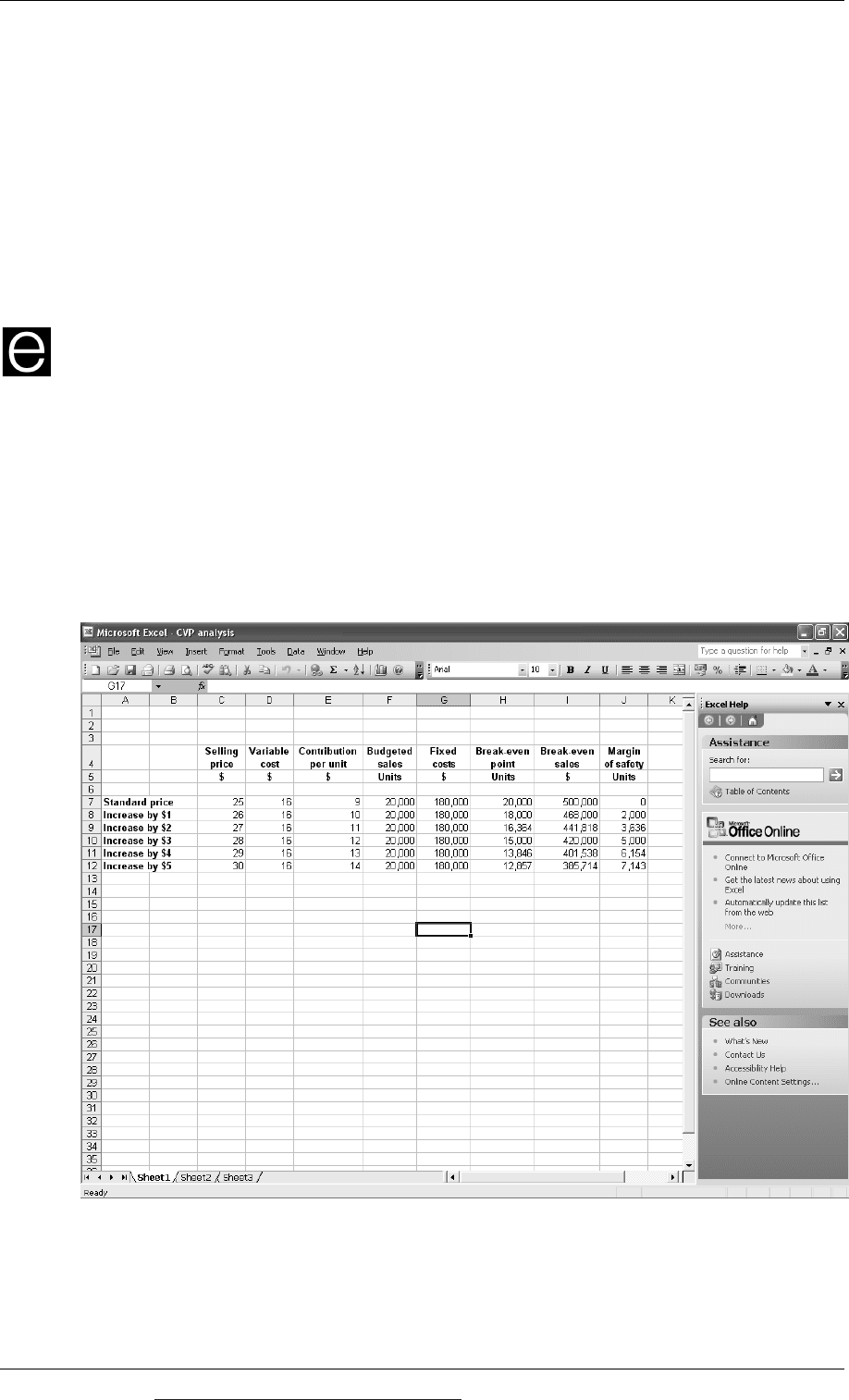
Example

Cost-volume-profit analysis is a technique in cost accounting that might be used to

prepare profit forecasts or to estimate what the profit might be at different selling

prices per unit or at different sales volumes. In this example, numbers might have

been entered in cells C7, D7, F7 and G7. All the other cells, except for the text cells,

will contain formulae.

The estimates for selling price, variable costs, budgeted sales units and fixed costs

can be amended simply by changing the numbers in C7, D7, F7 and G7. (However,

in this example, the text cells A8 – A12 might also need changing.

Paper F2: Management accounting

Graphical reproduction of spreadsheet data

Spreadsheets can be printed out and included in management reports. It is very

common in practice to find tables of figures produced in a spreadsheet to be

included as appendices in management reports.

In addition, the figures in a spreadsheet can be converted by the spreadsheet

program into graphical display format, and shown as graphs, bar charts or pie

charts. This facility can also be very useful for the preparation of management

reports.

For example, if a spreadsheet is used for linear regression analysis, it can be used to

show the line of best fit as a graph. Similarly, if a spreadsheet is used to prepare an

estimate of costs, the percentage of total costs made up by different items of cost

(direct materials, direct labour, production overheads etc) can be shown as a pie

chart or a bar chart.

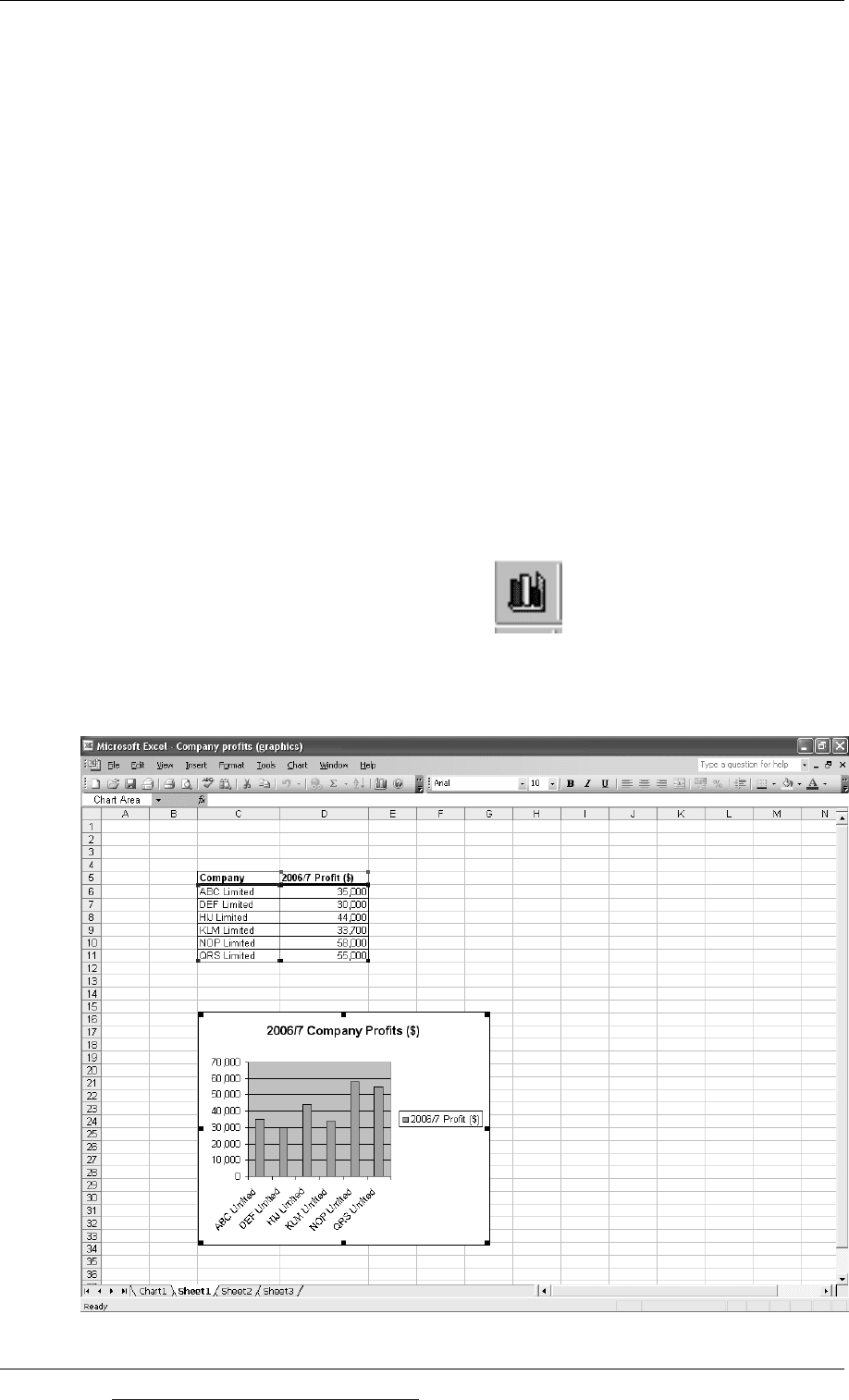
In the Microsoft Excel spreadsheet program, the facility to produce graphical

displays is provided by the Chart Wizard facility. A Chart Wizard icon is on the

menu bar and appears as follows:

The example below shows how the profits for six different companies can be shown

in the form of a graph using ‘Chart Wizard’.

ACCA F2 Management Accounting - 2010 - Study text - Emile Woolf Publishing

Подождите немного. Документ загружается.