Agoston M.K. Computer Graphics and Geometric Modelling: Implementation and Algorithms

Подождите немного. Документ загружается.

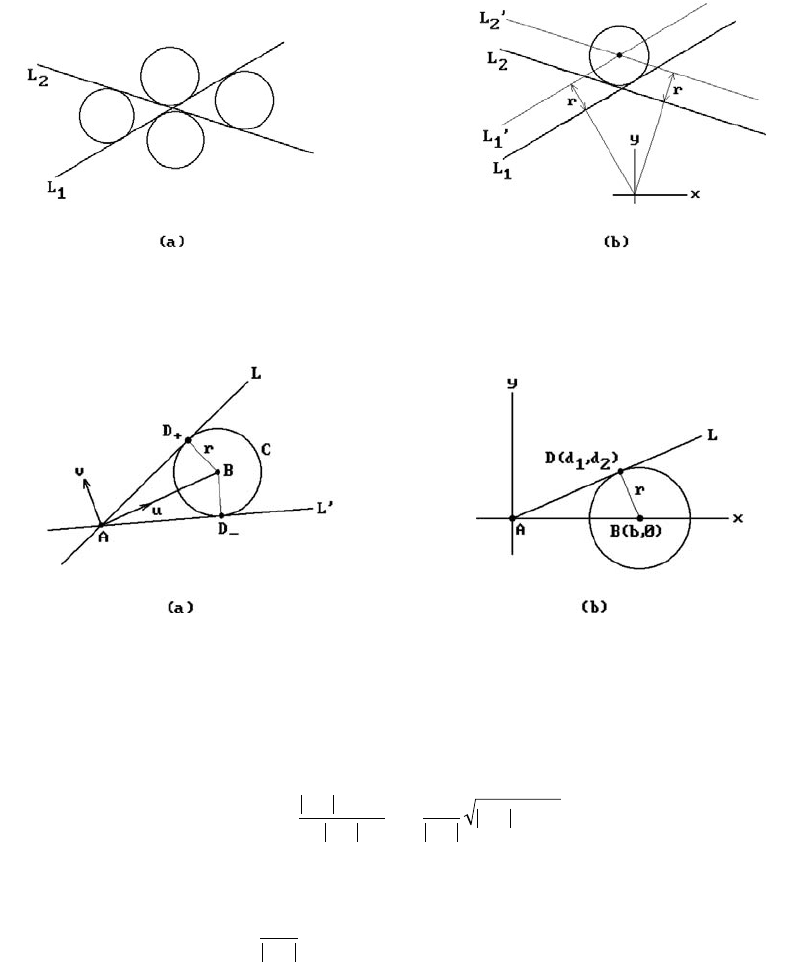
6.8.3 Formula. Let A be a point and C a circle with center B and radius r. Assume

that |AB|>r. There are two lines through A that are tangent to C and they intersect

C in the points D

deﬁned by

where u and v are the orthonormal vectors

Proof. Figure 6.22(a) shows the two lines L and L¢ that pass through A and are

tangent to C. By switching to the coordinate system deﬁned by the frame (A,u,v) we

may assume that A = (0,0) and B = (b,0). Let D = (d

). See Figure 6.22(b). The fol-

lowing equations are satisﬁed by D:

v==

()

u u and u u

12 21

,,.

AB v

±-

6.8 Circle Formulas 255

Figure 6.21. Circles of ﬁxed radius tangent to two lines.

Figure 6.22. Lines through a point tangent to a circle.

In other words,

If follows that

Since b corresponds to |AB| in the original problem, our solution translates into the

stated one in world coordinates.

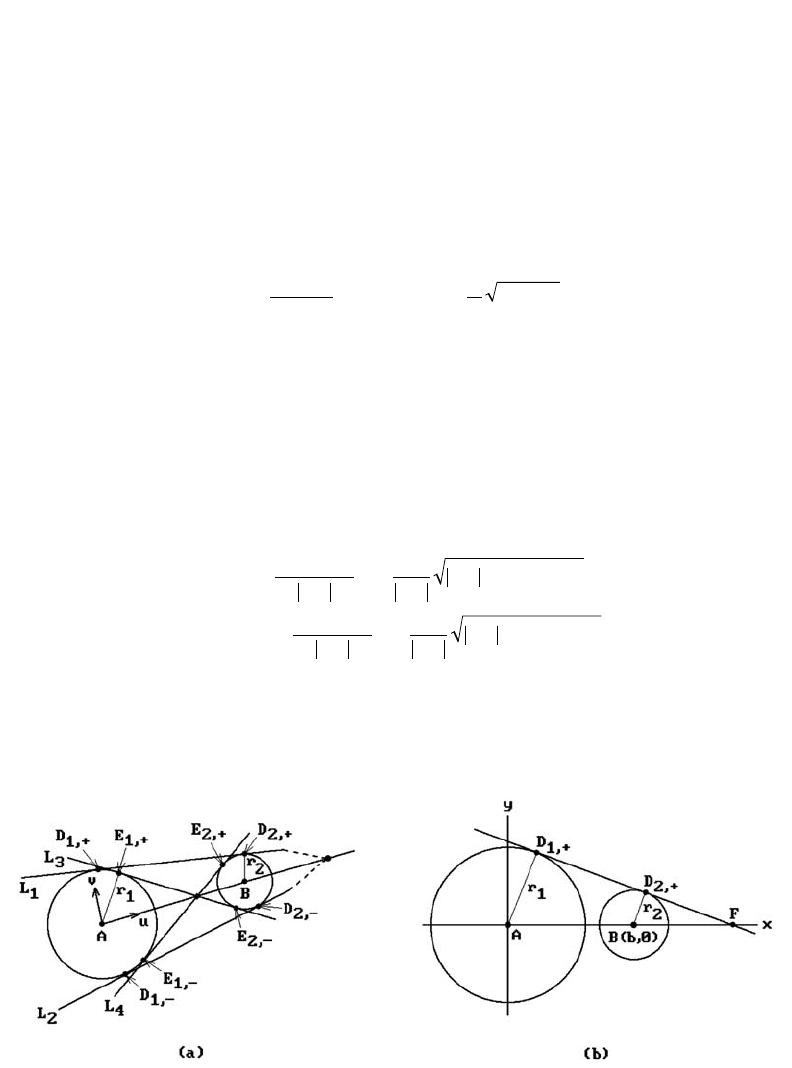
6.8.4 Formula. Consider two circles in the plane centered at points A and B with

radii r

and r

, respectively. Assume that |AB|>r

+ r

and r

> r

. Let D

i,±

and E

i,±

the points where the four lines L

that are tangent to both of these circles intersect

the circles. See Figure 6.23(a). Then

where A

= A, A

= B, e

=+1, e

=-1, and u and v are the orthonormal vectors

AB v

iii

rr r r

()

±--

()

±-+

()

and d

=± - .

db d r

dd b d

11 2

()

+=.

BD • BD

D•BD

256 6 Basic Geometric Modeling Tools

Figure 6.23. Lines tangent to two circles.

Proof. Note that the associated pairs of lines (L

) and (L

) intersect on the line

through the points A and B. We again switch to the coordinate system deﬁned by the

frame (A,u,v) and assume that A = (0,0) and B = (b,0), b > 0. See Figure 6.23(b). Let

F = A + sAB be the point where L

intersects the x-axis. Then

(6.38)

Because the triangles ADF and BEF are similar, we get that

(6.39)

Case 1: s > 1. In this case equation (6.39) implies that

Case 2: 0 < s < 1. In this case equation (6.38) implies that

In either case, since we now know F, we can now use Formula 6.8.3 to compute

i,±

and E

i,±

. For example, in Case 1,

Note that to use Formula 6.8.3 we must use the frame (F,-u,v). It is now a simple

matter to rewrite this formula in the form stated earlier.

6.8.5 Formula. Consider two circles in the plane centered at points A and B with

radii r

and r

, respectively. Assume that r

+ r

<|AB|<r

+ r

+ 2r. The circles of

radius r that are tangent to these circles have center C deﬁned by

where

CA u v=+ ± +

()

-erre

AB v

()

AF AB

BF AB

s1 .

v==

()

u u and u u

12 21

,,.

6.8 Circle Formulas 257

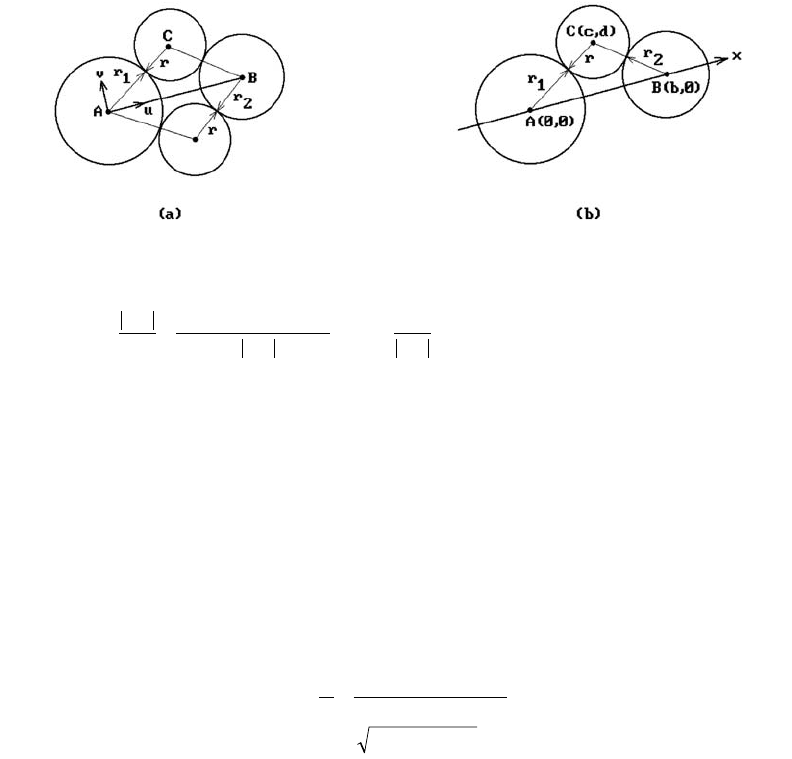
Proof. We can see from Figure 6.24(a) that there are precisely two circles of radius

r which are tangent to both circles. What we have to do is ﬁnd the intersection of

two circles: one has center A and radius r

+ r and the other has center B and radius

+ r.

We switch to the coordinate system deﬁned by the frame (A,u,v). Let A = (0,0) and

B = (b,0). See Figure 6.24(b). We must solve the equations

We get that

This translates to the desired formula in world coordinates since b corresponds to

|AB|.

This concludes our list of formulas involving circles. Other formulas can be found

in [Chas78] and [BowW83].

6.9 Parametric or Implicit: Which Is Better?

Two of the most common ways to present a geometric object X is via a parameteri-

zation or implicitly as the zeros of an equation. It is natural to ask which is better.

The advantages and disadvantages of these two representations are seen best in the

context of the following two tasks:

brr rr

yrrx

()

=± +

()

xy rr

xb y r r

+=+

()

+=+

()

rr rr

u u and u u=+

()

12 21

,,, ,.

258 6 Basic Geometric Modeling Tools

Figure 6.24. Circles of ﬁxed radius tangent to two circles.

Task 1: Generate some points that belong to X.

Task 2: Determine if a point q belongs to X.

Assume that X Õ R

. Suppose that

(6.40)

is a parameterization of X, where A Õ R

. Suppose also that

(6.41)

where f: R

Æ R.

Advantage of a parameterization: Task 1 is easy because all one has to do

is to evaluate the function p in (6.40) at

different values.

Disadvantage of a parameterization: Task 2 is hard because one has to ﬁnd a

value t that satisﬁes the equation p (t) = q.

Advantage of an implicit deﬁnition: Task 2 is easy because all one has to do

is check if f(q) = 0 for the f in equation

(6.41).

Disadvantage of an implicit deﬁnition: Task 1 is hard because one has to ﬁnd

values q for which f(q) = 0. Solving

equations is usually not easy.

Since both Tasks 1 and 2 are usually handy to be able to carry out in a modeler, it would

be nice if one could maintain both a parametric and an implicit representation for an

object. The implicit function theorem implies that locally a smooth manifold in R

has

both a parametric and implicit representation, at least in terms of C

•

functions. On the

other hand, in computer graphics, for computability reasons, one prefers polynomial

functions (sometimes rational functions are acceptable) and then the question

becomes harder. With the exception of a few well-known spaces, such as conics, ﬁnding

such representations is difﬁcult in general and falls into the domain of algebraic geom-

etry. See Chapter 10 in [AgoM05] for some answers to the question of how one can

convert from parameterizations to implicit representations and vice versa.

6.10 Transforming Entities

This section makes two simple but useful observations about transformations. The

ﬁrst has to do with how vectors transform.

Let M: R

Æ R

be an afﬁne map. The map M can be written uniquely in the form

M = TM

, where T is a translation and M

is linear transformation with M

(0) = 0. Let

v Œ R

, where we think of v as a vector. Let v¢ be the vector to which v is transformed

by the map M. Then

(6.42)

v v not v¢=

() ()()

Xqq=

()

{}

f0,

p:AXÆ

6.10 Transforming Entities 259

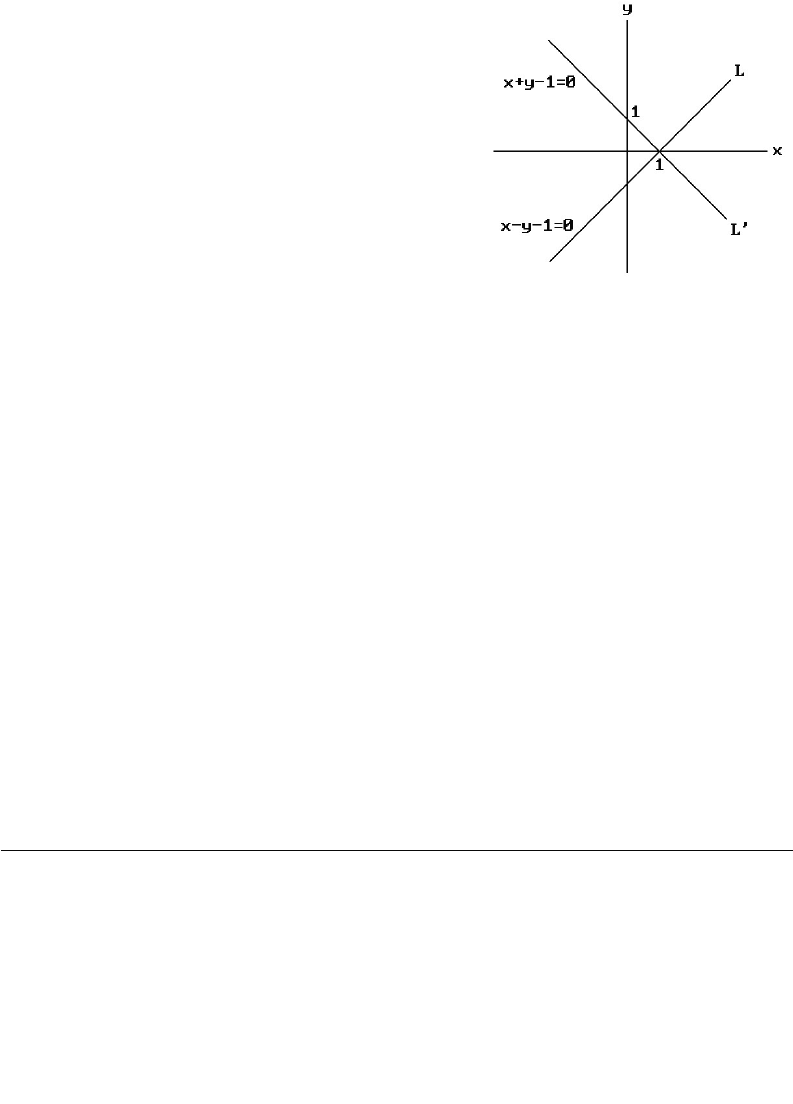
6.10.1 Example. Let L be the line in the plane deﬁned by

(6.44)

and let T be the rotation about the origin through the angle of ninety degrees. The

equations for T and T

-1

are

If L¢=T (L), then from what we just said above, the equation for L¢ is gotten from

equation (6.44) by substituting y and -x for x and y, respectively. This gives

(6.45)

That this is the correct answer can easily be checked. See Figure 6.26. Simply take

two points on L and ﬁnd the equation of the line through the image of these two points

under T. For example, the points (0,-1) and (1,0) map to (1,0) and (0,1), respectively,

and equation (6.45) contains these two points.

6.11 EXERCISES

Section 6.5

6.5.1 Find the intersection of the segments [(2,1),(6,-2)] and [(-1,-3),(7,1)].

6.5.2 Find a formula for the intersection of a ray with a segment in the plane.

6.5.3 Find the intersection of the line L deﬁned by

=- +

yx xy--

()

-=+-=110

Tx y T x y

yx y x

¢=- ¢=

¢= ¢=-

-1

xy--=10

6.11 Exercises 261

Figure 6.26. Transforming a line.

and the plane X with equation x + y - z = 2.

6.5.4 Find all intersections of the ray starting at the point p = (2,1) and direction vector

v = (1,-3) with the circle deﬁned by x

- 2x + y

= 0.

Section 6.6

6.6.1 Prove equation (6.19).

6.6.2 Prove Formula 6.6.2.

Section 6.7

6.7.1 Show that Formula 6.7.4 works for nonconvex polygons.

Section 6.8

6.8.1 Find the equation of the circle through the points p

= (2,1), p

= (3,3), and p

= (7,1).

Section 6.10

6.10.1 Find the equation of the parabola y = x

after it is rotated about the origin through an

angle of p/3.

6.12 PROGRAMMING PROJECTS

Section 6.5

6.5.1 Two-dimensional ray tracing

This project involves implementing a simple 2d ray-tracing program. Create the following

submenu for your main program

262 6 Basic Geometric Modeling Tools

When the user enters this menu, he/she should be presented with a view looking orthogonally

down on the plane. Then the menu items should cause the following actions to be taken when

activated:

Start Pt: This should let the user to graphically pick a point p on the screen.

Direction: This should ask the user for an angle q.

Start: This should start drawing the ray from p in the direction deﬁned by q. The ray

should continue, reﬂecting off of any polygonal curves and circles in the world,

until the user presses a key. If a ray does not meet any object, that is, it is about

to escape to “inﬁnity,” draw a short segment in that direction and then stop after

telling the user what has happened. Alternatively, rather than waiting for a key to

be pressed ask for a number k and quit drawing the ray after k reﬂections.

Be sure to include a delay each time the ray hits an object so that one can

watch the ray trace out its path in the world. Without this, the whole process will

happen so fast that one would only see a “ﬁnal” picture.

Example: This would display a sample world of objects for the user to use in this ray tracing

exercise.

An additional nice option in your program would be to allow the user to create his/her own

world of circles and closed or open polygons in the plane.

6.12 Programming Projects 263