Agoston M.K. Computer Graphics and Geometric Modelling: Implementation and Algorithms

Подождите немного. Документ загружается.

number of pixels) but can simply recompute the curve using the moved “control

data.”

No real constraints were placed on the basis functions above. However, in later

sections on Bézier curves and B-splines we shall see the usefulness of the following

properties:

(1) The functions should be nonnegative.

(2) The functions corresponding to point data should sum to 1.

(3) The functions should have compact support.

Properties (1) and (2) would imply that the curve lies in the convex hull of its control

points and property (3) essentially means that if a control point is moved only the

curve near that point changes. Properties (1)–(3) basically mean that the functions

form a partition of unity.

11.2.3 Spline Interpolation

The interpolation problems described in the last section and the functions that solve

them can be generalized.

Deﬁnition. A spline of degree m and order m + 1 is a function S : [a,b] Æ R for which

there exist real numbers x

, i = 0,..., n, with a = x

£ x

£ ...£ x

= b, so that

(1) S is a polynomial of degree £ m on [x

i+1

], for i = 0,..., n - 1, and

(2) S is a C

m-1

function.

The x

are called knots and (x

,...,x

) is called the knot vector of length n + 1 for

the spline. The intervals [x

i+1

] are called spans. If a knot x

satisﬁes x

i-1

< x

= x

i+1

...= x

i+d-1

< x

i+d

-1

=-•and x

n+1

=+•), then x

is said to be a knot of multiplicity d.

S is called a linear, quadratic, or cubic spline if it has degree 1, 2, or 3, respectively.

Note. One allows a =-•and/or b =+•in the deﬁnition of a spline. Only ﬁnite x

are called knots, however.

If one had to list the key terms that should always be intimately associated with

the concept of spline they would be “piecewise polynomial function,” “knots,” and

“differentiability.” Note that splines are more than just piecewise polynomials because

they satisfy a global differentiability condition. The piecewise Hermite interpolation

function described in the last section was not smooth enough to be called a cubic

spline.

The physical deﬁnition of a spline. A spline is a thin metal or wooden strip that

is bent elastically so as to pass through certain points of constraint.

Physical splines have been used for ages. For example, in the construction of ships’

hulls, the hull was modeled at full or nearly full size on a wooden ﬂoor in the “mold’s

loft.” This task, called “lofting,” was carried out by skilled “loftsmen” using such phys-

ical splines. When one tries to determine a mathematical description of the curves

generated by physical splines, one discovers something very interesting. Physics tells

11.2 Early Historical Developments 387

us that the strip will assume a shape that minimizes the strain. The equation for this

minimum energy problem is difﬁcult to solve directly, however, an approximation to

it can be solved and leads to a solution that is a cubic spline. We shall explain this a

little more in Section 11.6. At any rate, it is this ability of cubic splines to model curves

from physical splines, plus the fact that their low degree makes them easy to compute,

that makes them the most popular spline by far.

The spline interpolation problem: Given an integer k and real numbers x

and y

, i = 0,

..., n, with x

< x

< ...< x

, ﬁnd a spline g(x) of order k so that the x

are the knots for g

and g(x

) = y

11.2.3.1 Theorem. The spline interpolation problem has a solution.

Proof. For a general solution see [BaBB87] or [deBo78]. One can also prove this

using B-splines, which are discussed later. See [RogA90]. Here we shall only show the

existence of a solution in the important special case of a cubic spline. We rephrase

the problem as follows: Given points (x

), (x

),..., and (x

), ﬁnd cubic poly-

nomials p

(x), so that for i = 0,1,..., n - 1,

and for i = 1,2,..., n - 1,

In this situation we have 4n degrees of freedom and only 4n - 2 constraints. The two

extra degrees of freedom can be handled in several ways depending on how we choose

to specify m

and m

, the slope at the beginning and end of the spline, respectively.

We mention four approaches, but there are others.

End condition choices for interpolating splines:

(1) (Clamped end condition) We can specify the slopes m

and m

explicitly.

(2) (Bessel end condition) We can let m

and m

be the end slope of the interpo-

lating parabola for the ﬁrst, respectively, last three data points.

(3) (Natural end condition) We can require that the second derivative of the spline

vanishes at the ends. This amounts to requiring zero curvature of the spline at the

ends and is closer to what happens in the case of a physical spline. The spline will act

like a straight line near its endpoints. This type of spline is called a natural spline.

(4) (Periodic end condition) We require that the value of the spline and the value

of its ﬁrst and second derivative are the same at both endpoints. This is of interest

mainly in the context of closed spline curves.

In the ﬁrst approach we are obligated to specify the end conditions ourselves, whereas

in the other approaches it is done automatically for us. No matter what choice we

()

=¢

()

¢¢

()

=¢¢

()

px p x

ii i i

px y

ii i

()

388 11 Curves in Computer Graphics

make it will deﬁnitely inﬂuence the curve. As an example, consider the ﬁrst three

approaches in the context of a uniformly spaced spline curve that interpolates points

on an arc of a circle (we shall show how our results about spline functions applies

to spline curves shortly). One would like the curvature of the curve to be approxi-

mately constant since that holds for the circle. What one ﬁnds is the following (see

[Fari97]): With the correct choice of start and end tangents, the clamped end condi-

tion approach has the best curvatures, the Bessel end condition approach is the next

best, and the natural end condition approach is the worst because it forces the biggest

deviations from constant curvature near the endpoints.

For more on spline interpolation see [Beac91], [Fari97], or [RogA90]. Here we

only sketch the solution to the spline interpolation problem for clamped end

conditions.

Let us assume for the moment that we know the slopes m

= p

¢(x

) for i = 1,2,

..., n - 1. Assume further that we also know the slopes m

and m

at x

and x

, respec-

tively. Because the slopes are known, equation (11.21) deﬁnes the polynomials p

(x).

A simple computation using equation (11.21) shows that

where Dx

= x

i+1

- x

, and Dy

= y

i+1

- y

. Setting p

≤(x

) equal to p

i-1

≤(x

) leads to the

equation

for i = 0,1,..., n - 1, where d

= 1/Dx

. The matrix form of this system of equations is

(11.30)

where S

is the (n - 1) ¥ (n - 1) matrix

(11.31)

nn n

nnn

()

-- -

---

2000

200

02 00

000 0

0002

000 2

01 1

1122

223

32 2

221

dd d

dddd

ddd

dd d

ddd

...

. . . ... . .

...

ÁÁ

yym

100

()

dd d

nnn

()

dddddd

ii i iiii

mmmyy

-- - +

()

+= +

()

11 1 1

23DD,

¢¢

()

xm m y

yxmm

ii i i

iiii

11.2 Early Historical Developments 389

The tridiagonal symmetric matrix S

has all positive entries and is diagonally domi-

nant, which implies that it has an inverse. In other words, there is a solution to the

cubic spline interpolation problem and this solution is unique. The tridiagonal nature

of the matrix means that the system of equations can be solved very efﬁciently. One

needs only one forward substitution sweep (row operations starting from the top,

which eliminate the elements below the diagonal and change the diagonal elements to

1) and then one backward substitution sweep starting from the bottom. See [ConD72].

Finally, let us translate the above results to interpolating points in R

with a para-

metric curve. Suppose that we are given distinct real numbers u

, u

,..., u

and

points p

, p

,..., p

in R

, then there is a unique cubic spline p : [u

] Æ R

sat-

isfying p(u

) = p

. The individual cubic curves that make up p(u) are deﬁned by equa-

tion (11.25). All that is needed is to ﬁnd the tangent vectors v

at the points p(u

). Let

Then equation (11.30) becomes

(11.32)

The v

are solved for using this equation. The uniform spline case where u

i+1

- u

= 1

is of special interest. In that case we need to solve the following system:

(11.33)

Section 11.5.5 will look at another solution to the spline interpolation problem.

11.3 Cubic Curves

Cubic curves are the most popular in graphics because, as indicated earlier, the degree

is high enough for them to be able to satisfy the typical constraints one wants and yet

410 000

141 000

000 141

000 014

20 0

...

.........

... ...

.........

...

()

pp v

()

nn n

ppv

100

()

dd d

nnn--

()

d v

Dpp p

ii i i

and

=- =

d .

390 11 Curves in Computer Graphics

they are easy to compute. For that reason it is worthwhile to collect together in one

place some facts about them. The emphasis in this section will be on their basic matrix

representation and how it can be used to analyze the curves. Additional matrix rep-

resentations will be encountered in the sections on Bézier curves and B-splines. We

should point out though that matrix representations are not always the fastest or the

most numerically stable representations. See Section 11.15.

To begin with, it is easy to see, by collecting together terms with the same power

of u, that every cubic curve in R

can be written in the form

(11.34)

where the a

are vectors in R

. For example,

can be written as

Suppose that one wants to use a polynomial as in (11.34) to design curves. The a

are then the unknowns and in this representation of the function they are what has

to be determined. However, the same function can be speciﬁed in many different ways.

The most convenient way to specify the parameterization depends on what one is

doing. Specifying the a

directly is usually the least convenient. Hermite interpolation

was basically a case where one wanted to specify the curve by means of its endpoints

and its tangent vectors at those points. This is a more geometric approach but there

are others. Given that curves can be represented in different ways it is desirable to be

able to switch between representations. We show in this and later sections that matri-

ces can be used effectively for this task.

Notation. We shall abbreviate p(c) and p¢(c) to p

and p

, respectively.

From now on, unless stated otherwise, the domain of our cubic curve is assumed

to be [0,1]. This assumption leads to simpliﬁed formulas but the results in this case

translate easily into corresponding results for other domains. See the comments at

the end of this section.

Deﬁne matrices

(11.35)

Deﬁnition. The vectors a

are called the algebraic coefﬁcients of the cubic curve p(u).

The elements of B

are called its geometric or Hermite coefﬁcients.

()

u u u and

1, , .

pu u u u

()

372 0 31 201 015

,, , , ,, ,, .

pu u u u u u u

()

=+-+ +++

()

23 375 2

23 32

pu u u u

()

=+ + +aa a a

01 2

11.3 Cubic Curves 391

Note that

Furthermore, in analogy with equation (11.9),

Recall from (11.10) that the Hermite matrix M

, which is the inverse of the 4 ¥ 4

matrix on the left, is given by

(11.36)

By deﬁnition, A = M

. We have the following matrix equations:

(11.37)

where

The functions F

(u) are just the Hermite basis functions deﬁned earlier in (11.14). They

will now also be called blending functions because they blend the geometric coefﬁ-

cients into p. Equations (11.37) show that a curve can be manipulated by changing

either its algebraic or geometric coefﬁcients.

Derivatives of p can also be computed in matrix form:

(11.38)

where

(11.39)

---

0000

6633

6642

0010

()

==¢pu

UM B UM B F B ,

FUM==

() () () ()()

FuFuFuFu

1234

()

UM B

FB ,

---

2211

3321

0010

1000

0001

1111

0010

3210

=AB

p u and p u u u

()

=¢

()

=¢=

()

UA U A A3210

392 11 Curves in Computer Graphics

and

(11.40)

where

(11.41)

Before moving on to other matrix descriptions of a cubic curve we pause to show

how just the geometric matrix by itself already tells us a lot about its shape. A more

thorough discussion of the shape of curves can be found in Section 11.10. First of all,

we need to realize that only a limited number of shapes are possible here because

cubic polynomials have the property that their slope can change sign at most twice

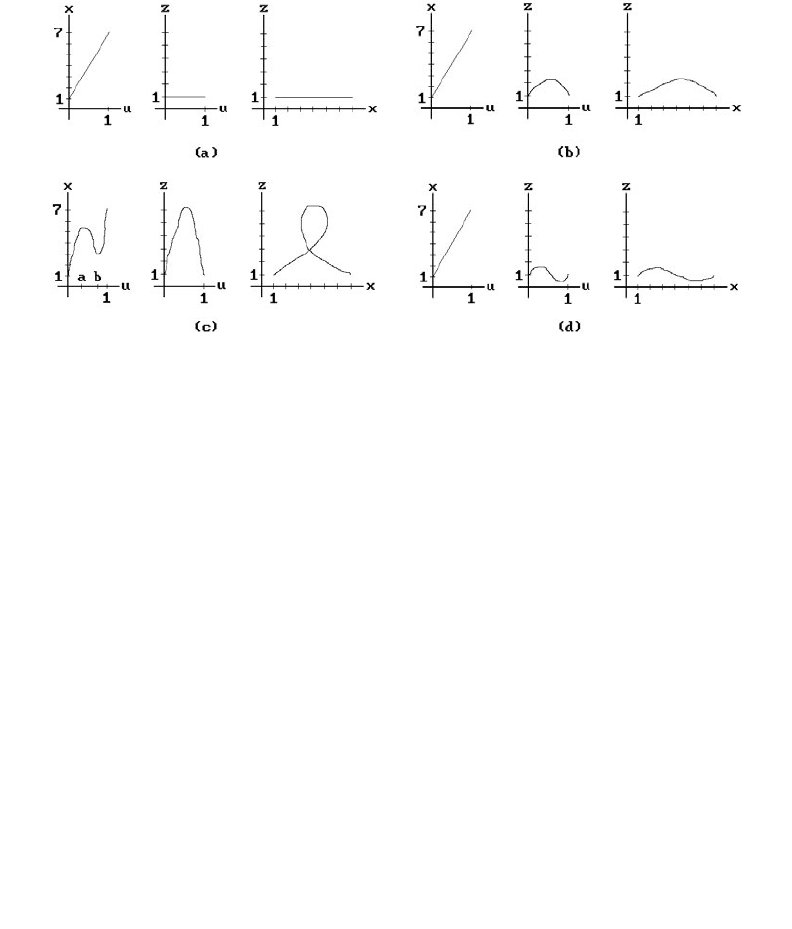
and they can have only one inﬂection point. For example, Figure 11.6(a) shows pos-

sible shapes and Figure 11.6(b) shows impossible ones. Secondly, although there may

be many ways to specify a cubic curve, it is uniquely deﬁned once one knows its geo-

metric coefﬁcients. To put it another way, if one can come up with a cubic curve that

has the same geometric coefﬁcients as some other cubic curve, then this will be the

same curve as the other one, no matter how the other one was deﬁned. Having said

that we shall now show how looking at the x-, y-, and z-coordinates of a cubic curve

separately and then combining the analysis can tell us a lot about its shape and

whether it has loops or cusps.

11.3.1 Example. Consider the following four geometric coefﬁcient matrices B

ab c d

()

131

731

600

13 1

73 1

60 10

13 1

73 1

20 0 40

13 1

73 1

6010

---

0000

12 12 6 6

6 642

¢¢

()

¢¢

==¢¢pu

UM B UM B F B ,

11.3 Cubic Curves 393

Figure 11.6. Possible and impossible cubic curves.

The problem is to sketch the corresponding curves p(u) without actually computing

the polynomials via formula (11.37).

Solution. Sketches of the curves are shown in Figure 11.7, but we want to give a

qualitative explanation for why they look like they do.

First of all, note that in all four cases the curve starts at (1,3,1) and ends at (7,3,1).

Let

Then y(0) = y(1) = 3 and y¢(0) = y¢(1) = 0. It follows that y(u) = 3 for all u and that each

curve lies in the plane y = 3. To analyze each curve we need only ﬁnd its projection

in the x-z plane. This will be done by analyzing x(u) and z(u).

Curve (a). The tangent vector at the beginning and at the end is (6,0,0). Since the

straight line

from (1,3,1) to (7,3,1) has the same tangent vector, this is the (only) solution. See

Figure 11.7(a).

Curve (b). See Figure 11.7(b). The function x(u) is just a linear function since it has

the right slope, namely, 6, at both ends. Because the slope of z(u) is 10 at 0 and -10

pu u

()

131 600,, ,,

pu xu yu zu

()

() () ()()

,, .

394 11 Curves in Computer Graphics

Figure 11.7. The cubic curves for Example 11.3.1(a)–(d).

at 1, the shape of the graph of z(u) can be realized by a parabola as shown in the

ﬁgure. The function z(u) achieves its maximum value at u = 0.5. (By uniqueness, since

a parabola is able to satisfy the given data, it must be the curve. Actually solving for

z(u) would give us

but we do not need this precise formula.) It follows that as u moves from 0 to 1, x(u)

increases steadily from 1 to 6 in a uniform way and the function z(u) starts at 1 and

increases until u = 0.5, then it decreases back to 1. This leads to the indicated sketch

of the projection of p(u) to the x-z plane.

Curve (c). See Figure 11.7(c). The graph of x(u) needs to have the shape shown since

its slope is 20 at both 0 and 1. It is a cubic. The only fact that we need to believe that

requires perhaps a little extra experience with functions is that the local maximum

and minimum occur at some values a and b, respectively, where 0 < a < 0.5 < b < 1.

The function z(u) has slope 40 at 0 and -40 at 1. Therefore, since this can again be

realized by a parabola which takes on its maximum value at u = 0.5, it is that parabola.

Its actual formula happens to be

but this is again not important for what we are doing. All that we need to

know is that as u moves from 0 to a, the x-coordinate of p(u) is increasing and

so is the z-coordinate. As we move from a to 0.5, x is decreasing, but z is still

increasing. Moving from 0.5 to b, both x and z are decreasing. Finally, as u moves

from b to 1, x is increasing, but z is decreasing. The reader should check that the

x- and z-coordinates of the self-intersecting loop shown on the right in Figure

11.7(c) behave in the same way as one moves from the left to the right endpoint of

that curve.

Curve (d). See Figure 11.7(d). The graph of x(u) is again a straight line and the

shape of the graph of z(u) is forced by its slope of 10 at both ends to be the cubic

as shown. The rest of the argument is, like for curve (c), based on an analysis of

the regions where x and z are increasing and decreasing. This ﬁnishes Example

11.3.1.

Example 11.3.1 and others such as Exercise 11.3.2 should begin to give the reader

a feel for how changing p

and p

affects a curve.

One other useful matrix form is the one for a cubic curve that interpolates four

points p

, p

, and p

. Although equation (11.8) already described a general solu-

tion for this problem, it is worthwhile to state the special uniform case explicitly. That

is the case where the u

are chosen to be the numbers 0, 1/3, 2/3, and 1, in other words,

= p(i/3). Let

zu u

()

=- -

()

+20 0 5 6

zu u

()

=- -

()

+505225

..,

11.3 Cubic Curves 395

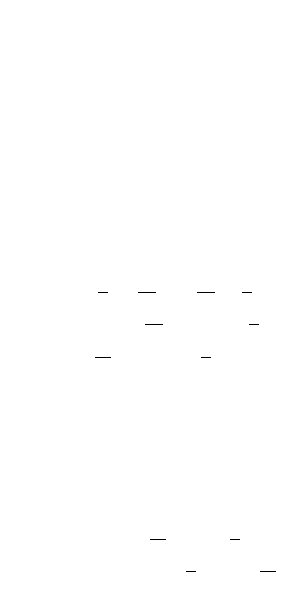
Then the so-called four-point matrix form of a cubic curve is

(11.42)

where the four-point matrix M

is deﬁned by

(11.43)

The geometric matrix B

and P are related by the equation B

= LP, where

(11.44)

The discussion up to here has centered on cubic curves with domain [0,1]. What

happens in the case of a different domain [a,b]? One can give a similar analysis, except

that the “geometric coefﬁcients” for such a cubic curve would have to be based on the

values and tangents at a and b, rather than at 0 and 1. Other than that one could

proceed pretty much as before. Note that the Hermite matrix M

can no longer be

used, but there would be a matrix that plays the same role but based on a and b.

Exercise 11.3.4 asks the reader to work out one example of such a change.

11.4 Bézier Curves

This section and the next will deal with curves that are deﬁned by control points but

do not interpolate them in general. We shall return to the interpolation problem in

Section 11.5.5.

Although the geometric coefﬁcients approach to deﬁning curves is a big improve-

ment over having to specify the algebraic coefﬁcients, specifying tangent vectors in

an interactive computer graphics environment is still somewhat technical. A better

way allows a user to specify these vectors implicitly by simply picking points that

suggest the desired shape of the curve at the same time. Figure 11.8 shows a cubic

curve p(u) which starts at p

and ends at p

. It is very easy to specify the tangent lines

LMM==

1000

0001

918

1000

()

= UM P

396 11 Curves in Computer Graphics