Agoston M.K. Computer Graphics and Geometric Modelling: Implementation and Algorithms

Подождите немного. Документ загружается.

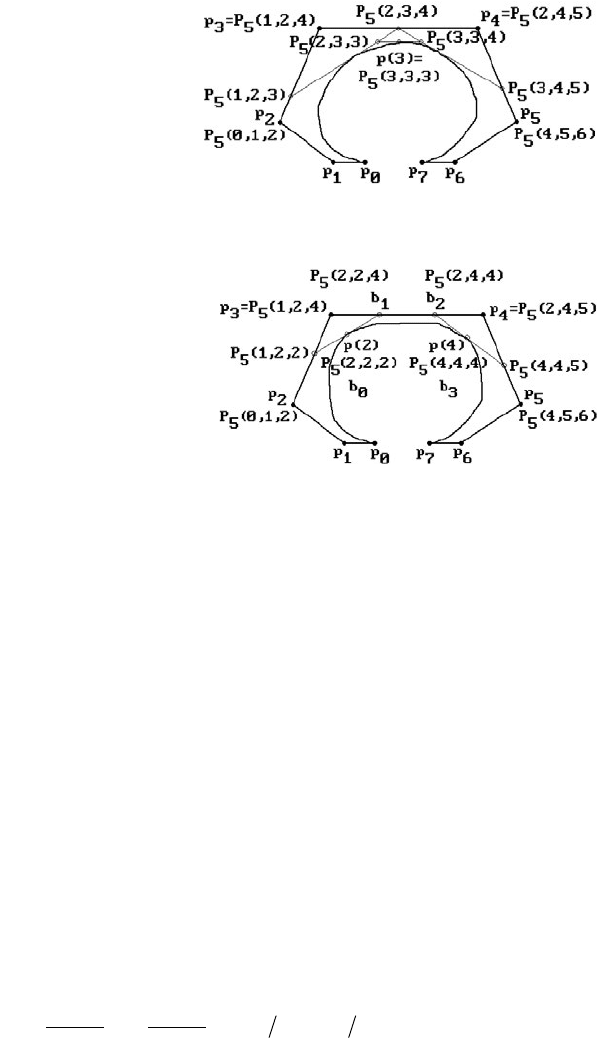
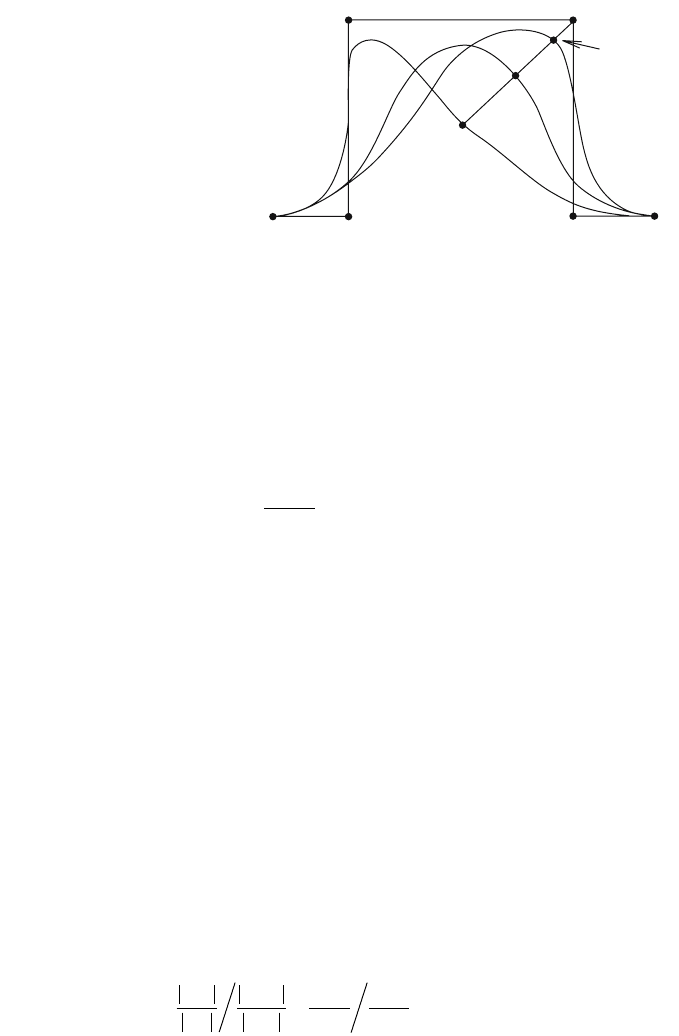
Figure 11.24 shows how Algorithm 11.5.2.2 computes the value of the cubic B-spline

p(u) with knot vector (0,0,0,0,1,2,4,5,6,6,6,6) at u = 3. In that case, i = 5 and p(3) =

(3,3,3).

There is more geometry hidden in the formalism above. Given a blossom we can

use equations (11.90) and (11.96) to deﬁne the Bézier and de Boor points, respectively.

In other words, we have a way to switch between a Bézier and a B-spline represen-

tation for a B-spline curve. We show how this works with an example.

11.5.2.11 Example. Let p(u) be a cubic B-spline p(u) with knot vector (t

) =

(0,0,0,0,1,2,4,5,6,6,6,6) and consider the interval [2,4]. Using the notation of Theorem

11.5.2.9 that interval corresponds to the values j = 5, k = 4, and 2 £ ᐉ £ 5. In equation

(11.90) we would have d = 3. Using the blossom of the curve p(u) over [2,4] = I

] we can compute both the associated de Boor points p

= P

(0,1,2), p

= P

(1,2,4),

= P

(2,4,5), and p

= P

(4,5,6) and the Bézier points b

= P

(2,2,2), b

= P

(2,2,4),

= P

(2,4,4), and b

= P

(4,4,4). See Figure 11.25. From this it is easy to see the rela-

tionship between the Bézier and de Boor points. Consider the three points p

(1,2,4) = P

), b

= P

(2,2,4) = P

), and p

= P

(5,2,4) = P

). Using

barycentric coordinates and the linearity of P

with respect to its ﬁrst coordinate, we

see that

Similarly, b

= P

(4,2,4) = P

), and

bpppp

434

34 14=

()

11.5 B-Spline Curves 427

Figure 11.24. The de Boor algorithm for

B-splines using blossoms.

Figure 11.25. Computing Bézier points

from the de Boor points.

In particular, the points p

, b

, and p

are collinear. Furthermore, the point b

divides the segment [p

] in the same proportion as t

divides the interval [t

Similarly, the point b

divides the segment [p

] in the same proportion as t

divides

the interval [t

The computations in Example 11.5.2.11 easily generalize. There was nothing

special about our knots and j = 5. Consider an arbitrary cubic B-spline p(u) with knots

and control points p

. With respect to [t

j+1

], t

< t

j+1

, we have

Deﬁne points

Then we can easily show like in Example 11.5.2.11 that

and

11.5.2.12 Theorem. If t

£ u £ t

j+1

, then the cubic curve traced out by the function

p(u) deﬁned by equations (11.95) and the curve traced out by the Bézier curve p(u)

deﬁned on [0,1] by equation (11.49) for control points b

3j-6

, b

3j-5

, b

3j-4

, and b

3j-3

are

the same.

Proof. This is an easy consequence of the validity of the de Casteljau and the de

Boor algorithms.

Theorem 11.5.2.12 can be rephrased as saying that each cubic B-spline curve can

be thought of as a collection of cubic Bézier curves. Comparing control points, each

knot interval contributes two de Boor points and four Bézier points under this

correspondence.

The de Boor algorithm also shows us how to insert knots. The reason one might

want to insert knots is to allow more ﬂexibility in subsequent manipulations. As usual,

assume that we have a B-spline p(u) of order k with knot vector K = (t

,...t

n+k

)

deﬁned by equation (11.95) and suppose that we want to add a new knot t, where t Œ

h+1

). Let K* = (t

,..., t

,t,t

h+1

,..., t

n+k

) be the new knot vector and let N

i,k

(u)

be the spline functions deﬁned recursively by equations (11.69) but with respect to

the new knot vector K*. We want to ﬁnd new control points p

so that

bpp

36 35 1

34 11 33 111

j jjjj j jjjj

Pttt Pttt

--+

- ++ - +++

()

,, , ,, ,

,, , ,, .

jjjjj jjjjj

Pt tt and Pt tt

--+ -++

()

211 111

,, ,, .

bpppp

434

14 34=

()

428 11 Curves in Computer Graphics

(11.97)

11.5.2.13 Theorem. The new control points for equation (11.97) are deﬁned by

where

Proof. See [Boeh80] or [Seid89]. Figure 11.26 shows the idea behind the proof. We

have inserted the knot t = 3 into the knot vector (0,0,0,0,1,2,4,5,6,6,6,6) used in Figure

11.25.

Inserting knots does not change the shape of the curve but increases the number

of control points; however, in contrast to Bézier curves we do not raise the degree of

the curve by doing this.

Theorem 11.5.2.13 shows how to insert a single knot. Sometimes one wants to

insert more than one knot at a time into a knot vector. The next theorem shows how

to do that. We again assume that we have a B-spline p(u) with knot vector K = (t

...t

n+k

), but this time we want to replace K with a new knot vector K* = (s

,...,

m+k

), m ≥ n. If N

i,k

(u) are the spline functions associated to K*, we want to ﬁnd the

new set of control points p

, so that

(11.98)

11.5.2.14 Theorem. (The Oslo Algorithm) The control points for equation (11.98)

are deﬁned by

ajm

=££

pu N u

jk j

()

aihk

hk ih

hin

ik i

=££-+

-+££

=+££+

10 1

011

pp p

iii ii

,=+-

()

pu N u

()

11.5 B-Spline Curves 429

Figure 11.26. Boehm knot insertion.

where the a

i,j

are deﬁned recursively by

Proof. See [CoLR80].

We ﬁnish this section with several other theorems that follow easily from the

multiafﬁne map approach to splines. First of all, an important fact that drops out of

the formalism is the differentiability of the functions N

i,k

(u), which is not totally

obvious from their recursive deﬁnitions.

11.5.2.15 Theorem. If t = t

j+1

= t

j+2

= ...= t

j+m

is a knot of multiplicity m £ k for

i,k

(u), then N

i,k

(u) is C

k-1-m

at t.

Proof. See [Seid89].

11.5.2.16 Theorem. (Curry-Schoenberg Theorem) All splines are linear combina-

tions of B-splines.

Proof. See [Seid89].

One can use Theorems 11.5.2.12 and 11.5.2.15 to ﬁnd the Bézier control points of

a spline of order k. Simply keep inserting knots until all have multiplicity k - 1. At

that point the de Boor points reduce to the Bézier points.

11.5.2.17 Theorem. (Variation diminishing property) A plane (line in planar case)

intersects a B-spline in no more points than it intersects the control polygon.

Proof. See [LanR83], [Seid89], or [PieT95]. In particular, this theorem applies to

Bézier curves.

One important point about all the results in this section is that the proofs are very

short and straightforward. The reader should have little trouble ﬁlling in those that

are omitted.

11.5.3 Rational B-spline Curves

Although B-splines curves represent a very large class of curves, they are unable to

represent some very simple curves exactly. It is easy to show that conics like circles

and ellipses cannot be represented by polynomial curves and so B-spline curves can

only approximate them. This is a drawback because conics are curves that one often

wants to represent.

Fortunately, all is not lost. Conics can be represented by rational curves via a

simple trick. We show how this works in the case of a circle. Consider the circle of

aiftst

elsewhere

iji

jk i

ik i

ik jk

ik i

,, ,

=££

++-

430 11 Curves in Computer Graphics

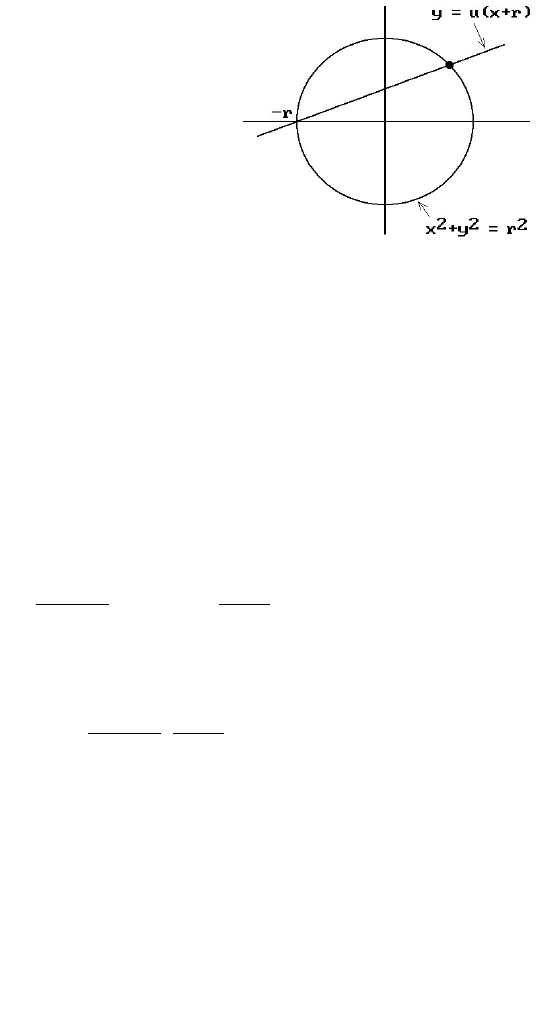
radius r shown in Figure 11.27. Every nonvertical line through (-r,0) can be

parameterized by its slope u and satisﬁes the equation

(11.99)

Solving for the intersection of this line and the circle

leads to the solution

and the parameterization

(11.100)

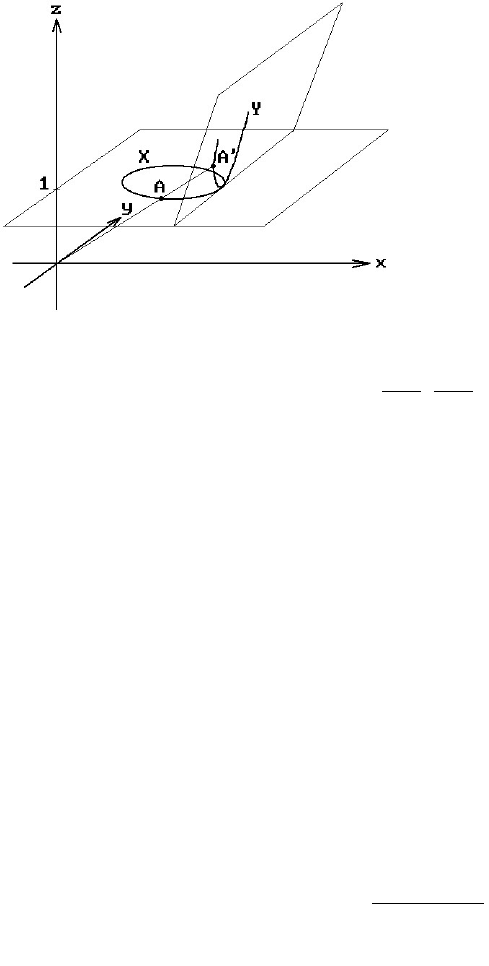
Another argument for showing that conics have rational parameterizations comes

about by using projective geometry and homogeneous coordinates. It is a well-known

fact (Theorem 3.6.1.1 in [AgoM04]) that all conics are projectively equivalent. In fact,

every conic X in the plane z = 1 in R

is the central projection of a parabola Y in some

other plane. See Figure 11.28. Furthermore, a parabola is the only conic that has a

polynomial parameterization. Now the standard parabola y = x

in R

can be

parameterized by u Æ (u,u

), so that our parabola Y can be parameterized by a

quadratic curve

(11.101)

since it is obtained from the standard one by a linear change of variables and such a

transformation does not change the degree of the parametrization. It follows that the

conic X has a rational parametrization of the form

uxuyuzuÆ

() () ()()

()

and y

()

xyr

222

yuxr=+

()

11.5 B-Spline Curves 431

Figure 11.27. Deﬁning a rational parameterization of

the circle.

because the central projection is gotten simply by dividing by the z-coordinate. But

we can think of equation (11.101) as deﬁning a conic with homogeneous coordinates

in projective space P

. The important observation is then that conics do have

polynomial representations if we use homogeneous coordinates.

In summary, we have shown that we can handle a larger class of curves if we use

homogeneous coordinates. In that setting, the analog of equation (11.67) is

(11.102)

where the b

(u) are suitable basis or blending functions and the P

are points described

with homogeneous coordinates. Everything we did earlier for polynomial curves

applies to the curves deﬁned by equation (11.102) since the nature of the coordinates

did not play a role. In particular, we have the obvious notions of Bézier and B-spline

curves for homogeneous coordinates. Furthermore, if we write P

in the form P

), then the projective space curve deﬁned by P(u) projects to the curve

(11.103)

where p

= (x

). There are several important special cases of such curves.

Deﬁnition. The curve p(u) deﬁned by equation (11.103) is called a rational Bézier

curve if its domain is [0,1] and b

(u) = B

i,n

(u). (The B

s,t

(u) are the functions deﬁned

by equation (11.50).) The curve p(u) is called a rational B-spline curve of order k if the

wb u

ii i

()

Pu b u

()

P ,

()

432 11 Curves in Computer Graphics

Figure 11.28. Projectively equivalent

ellipse and parabola.

(u) are B-splines of order k. The curve p(u) is called a nonuniform rational B-spline

(NURBS) curve of order k with domain [a,b] if b

(u) = N

i,k

(u) with respect to a knot

vector

(The N

i,k

(u) are the B-splines deﬁned by equations (11.69).) In any case, the points p

are called the control points of the curve p(u) and the numbers w

are called its weights.

The ordinary Bézier and B-spline curves are clearly a special case of the rational

ones since we get them by using weights that are all equal to 1. Note further that if

we deﬁne the function R

(u) by

(11.104a)

then

(11.104b)

so that p(u) is again a curve of a form (like that of equation (11.67)) that we have seen

many times before.

Deﬁnition. The functions R

(u) in equations (11.104) are called the rational basis

functions for the curve p(u).

NURBS curves (and surfaces) have become very popular in recent years and a

number of modeling programs are based on them. Some general references for these

and rational Bézier curves are [PieT95], [Pieg91], [Fari95], [Roge01], or [RogA90]. In

the rest of this section we shall look at some examples and properties of NURBS

curves, leaving a discussion of how to compute them efﬁciently to the next section.

11.5.3.1 Example. Suppose that we want to ﬁnd a NURBS representation for the

unit circle.

Solution. Consider the ﬁrst quadrant of the unit circle. By equation (11.100) we have

the rational parameterization

In homogeneous coordinates this can be written as

(11.105)

Pu u u u

()

=- +

()

1201

1001 0200 1001

,,,

,,, ,,, ,,,.

for u

()

[]

,, ,.

pu R u

()

p ,

wb u

()

U u a auu ub b

kk n

()

( ,..., , , ,..., , ,..., ).

1243412434

11.5 B-Spline Curves 433

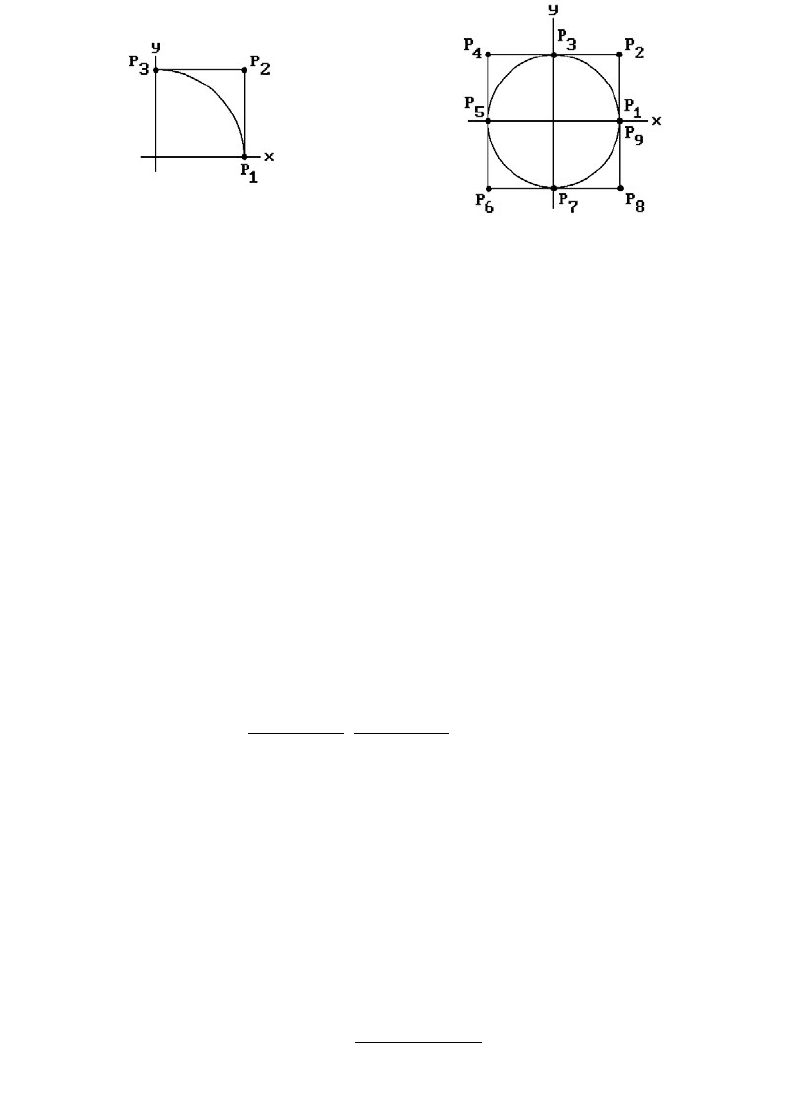
The Bézier approach to describing this curve is to look for three homogeneous control

points P

, P

, and P

so that

(11.106)

Equating the coefﬁcients of the u’s in the two equations (11.105) and (11.106) for P(u)

gives that

The corresponding p

are shown in Figure 11.29(a). Using these P

as control points

and the knot vector (0,0,0,1,1,1) gives us the NURBS curve that describes the ﬁrst

quadrant of the unit circle. A NURBS representation for the second quadrant can

easily be obtained from this one by rotating the control points about the y-axis by

180 degrees. Alternatively, reparameterizing to [1,2], a parameterization q(u) for this

second quadrant is

and we can solve for the new control points as before. At any rate, the new control

points are

Finally, rotating our control points by 180 degrees about the x-axis gives us the com-

plete NURBS representation for the whole unit circle. It is easy to check that the

parameterization can be written in the form

wN u

ii i

()

PP P

34 5

0202 1101 1001=

()

,,, , ,,, , ,,,and

for u

()

[]

12,, ,,

PP P

12 3

1001 1101 0202=

()

,,,, ,,, , ,,, .and

Pu u u u u

()

=+ -

()

+-+

()

121

321

PPP

PPPPPP.

434 11 Curves in Computer Graphics

Figure 11.29. The circle as a rational B-spline.

where the weight sequence (w

,...,w

) is (1,1,2,1,1,1,2,1,1) and the knot vector is

(0,0,0,1,1,2,2,3,3, 4,4,4). The points p

are shown in Figure 11.29(b).

Although Example 11.5.3.1 found a NURBS representation for the unit circle, it

is not a good one because it does not distribute points uniformly along the circle. The

problem is with the rational function parameterization that we used as a starting

point. [Till83] shows how one can get a better parameterization by a rational trans-

formation of the form

Next, there is a geometric interpretation of the weights. To emphasize the depend-

ence of the function p(u) deﬁned by equation (11.103) on its weights we shall include

a reference to the weights in the parameters of the functions below along with any

values that may have been assigned to them. See Figure 11.30, where

where the R

are the rational basis functions of p(u), then one can show that

It follows that

In other words, the weight w

is just the cross-ratio of the four points p

, q, r, and q

The following geometric facts can be proved:

iii

--pr

11a

rqp

qqp

()

and,

ab==

()

R u w and R u

ii i

;,1

qr q==

()

=π

()

p u w p u w and p u w or

iiii

;, ;, ; .01 01

at b

ct b

11.5 B-Spline Curves 435

Figure 11.30. The geometric interpreta-

tion of rational B-spline

weights.

(1) Increasing or decreasing w

will increase or decrease b which pulls the curve

toward p

or pushes it away from p

, respectively.

(2) Increasing or decreasing w

will push the curve away from p

or pull it toward

, j π i, respectively.

(3) The points q

lie on the line segment [q,p

(4) As q

approaches p

, b approaches 1 and w

approaches inﬁnity.

We ﬁnish by listing a few of the important properties of NURBS curves.

11.5.3.2 Theorem. Let p(u) be a NURBS curve of order k with domain [0,1], knots

, control points p

, and weights w

> 0.

(1) The rational basis functions R

(u) for p(u) satisfy R

(u) ≥ 0 and

(2) The curve p(u) interpolates the ﬁrst and last point. More precisely, p(0) = p

and p(1) = p

(3) (Local control) Changing the control point p

or weight w

only changes the

formula for p(u) over the interval (u

i+k

(4) (Projective invariance) If the curve p(u) is transformed by a projective trans-

formation, the formula for the new curve is gotten simply by transforming the homo-

geneous control points (equation (11.102) and then projecting back to R

to get

another formula like equation (11.103).

(5) (Local convex hull property) The curve p(u) satisﬁes a strengthened convex

hull property like the ordinary B-splines, namely, for each i, p([u

i+1

]) is contained

in the convex hull of the control points p

i-k+1

, p

i-k+2

,..., p

(6) (Variation diminishing property) A plane (line in planar case) intersects the

curve p(u) in no more points than it intersects the control polygon.

Proof. See [PieT95]. The projective invariance property is stronger than afﬁne

invariance. Ordinary B-splines are afﬁnely invariant but not projectively invariant.

Finally, although rational Bézier and B-spline curves are deﬁned as projections

of ordinary Bézier and B-spline curves in R

to the plane w = 1, it turns out that the

associated correspondence between ordinary splines in R

and ordinary splines in R

is not as natural as one might want. For example, not every C

Bézier and B-spline

curve p(u) in R

with simple knots is a projection of a spline curve q(u) in R

with

simple knots. To ﬁnd a curve q(u) that projects to p(u) we would have to allow q(u)

to have multiple knots. See [Fari89] for a discussion of this and the condition that

guarantees that a C

curve with simple knots is a projection of a C

curve with simple

knots.

11.5.4 Efﬁcient B-Spline and NURBS Curve Algorithms

As mentioned earlier, B-spline and NURBS curves are used a lot. Fortunately, although

their deﬁnitions seem somewhat complicated and it is certainly more work than

()

436 11 Curves in Computer Graphics