Agoston M.K. Computer Graphics and Geometric Modelling: Implementation and Algorithms

Подождите немного. Документ загружается.

12.2 Surfaces of Revolution 477

Since p(1,p/4) = p, it follows that

are a basis for our tangent plane. Finally,

is a normal vector to the plane, so that its equation is

12.2.2 Example. Assume that S is the surface of revolution obtained by rotating

the segment X = [(3,1),(3,3)] about the x-axis. We want to ﬁnd the tangent plane to S

at p = (3,0,2).

Solution. The surface S is parameterized by

and

∂

qqq

∂

∂q

qqq

y and

yyy, ,cos ,sin , , sin , cos .

()

()()

()

py y y, , cos , sinqqq

()

22220xyz--+=.

222 122 0,, ,, ,, ,--

()

∑

()

()()

=xyz

∂

∂q

14 14 2 2 2,,,,

()

=- -

()

∂

()

∂

()

and

∂

∂q

p14 11212 14 0 22,,, , ,,

Figure 12.4. Interesting surfaces of revolution.

Since p(2,p/2) = p, it follows that

are a basis for our tangent plane. Finally,

is a normal vector to the plane, so that its equation is

Next, if we rotate a semicircle about an axis whose endpoints lie on the axis, then

we get a sphere. In the case of the semicircle of radius r about the origin, we can

parameterize its points with the map

This leads to the following parameterization of the sphere of radius r about the origin:

(12.5)

See Figure 12.5(a). The partial derivatives

(12.6)

deﬁne the tangent planes except at the two poles (±r,0,0) where they vanish. The

tangent planes at those two points have to be handled as a special case unfortunately.

If we rotate a circle about an axis and if this circle does not meet the axis, then we

get a torus. As a special case, let T be the torus obtained by rotating the circle of radius

r with center (0,R,0), r < R, about the x-axis. See Figure 12.5(b). Here is another natural

way to visualize the standard parameterization of T. Let P

be the plane through the x-

axis that makes an angle q with the x-y plane. This plane intersects T in a circle C

with

center Ru

, where u

= (0,cosq, sinq) is the unit vector in the y-z plane that makes an

angle q with the y-axis. Parameterizing the points of C

by the angle f that the ray from

the center of C

makes with the x-axis corresponds to the map

∂

∂q

fq f q f q

rr, , sin sin , sin cos

()

∂

∂f

fq f f q f q

rr r, sin , cos cos , cos sin

()

prr rfq f f q f q, cos , sin cos , sin sin .

()

ffffpÆ

()

[]

r r forcos , sin , .0

x -=30.

200 302 0,, ,, ,, ,

()

∑

()

()()

=xyz

∂

∂q

22 22 200,,,,

()

∂

∂q

and

22 001 22 020,,, ,,,

()

() ( )

()

478 12 Surfaces in Computer Graphics

If we rotate half of a parabola about its axis, then we get a paraboloid of revolution

(also called an elliptic paraboloid). See Figure 12.5(c). If we do the same thing to a

hyperbola, we get a hyperboloid of revolution (also called a hyperboloid of one sheet).

12.2.4 Example. Let S be the paraboloid of revolution obtained by rotating the

part of the parabola x = y

, y ≥ 0, about the x-axis. We want to ﬁnd the tangent plane

and normal to S at p = (4,0,2).

Solution. The standard parameterization for S is

Since p(4,p/2) = (4,0,2) and

evaluating these vectors at (4,p/2) and taking the cross product gives us that (1/2,0,

-2) is a normal vector, so that

is the equation for the tangent plane.

12.3 Quadric Surfaces and Other Implicit Surfaces

Like the conic curves, quadric surfaces are an important shape for CAGD. A quadric

surface is a subset of points (x,y,z) in R

which satisﬁes a general quadratic equation

of the form

(12.9)

A complete classiﬁcation of the solutions to equation (12.9) can be found in Section

3.7 in [AgoM04] and we shall not repeat it here. Omitting the degenerate cases, one

gets the basic ellipsoids, cylinders, cones, paraboloids, and hyperboloids. Figure

12.5(a) and (c) showed a sphere (a special case of an ellipsoid) and paraboloid. Figure

12.6 shows examples of the others. Clearly, many mechanical parts have such shapes.

In an interesting paper, Goldman ([Gold83]) analyzes quadrics that are surfaces of

ax by cz dxy exz fyz gx hy iz j

222

0+++++++++=.

xz-+=440,

120 2 402 0,, ,, ,, ,-

()

∑

()

()()

=xyz

∂

qqq

∂

∂q

qqq

xxx

, , cos , sin

, , sin , cos ,

()

px x x x, , cos , sin .qqq

()

480 12 Surfaces in Computer Graphics

12.3 Ouadric Surfaces and Other Implicit Surfaces 481

revolution (like the cyclinder, ellipsoid, paraboloid, cone, and hyperboloids) and

shows that they make good candidates for primitives in modeling systems because

one can classify their intersections.

A fundamental question for a quadric surface like for all surfaces is how one

can ﬁnd a normal vector and an equation for the tangent plane at a point. Since

many of these surfaces are surfaces of revolution, we could apply the methods

developed in the last section. We could also use the fact that these surfaces can be

parameterized and tangent planes are easily computed from parameterizations.

Here, rather than using either of these two approaches, we shall describe another

powerful method. Quadric surfaces are a special case of implicit surfaces. An

implicit surface S in R

is a surface that is the set of zeros of a function f : R

Æ R,

that is,

It is a well-known fact that if p Œ S, then the gradient to f at p, —f(p), is a normal

vector to S at p (assuming that the function f is differentiable). This means that com-

puting normals for implicit surfaces is trivial. Of course, once one has the normal,

then the tangent plane is easily expressed in the point-normal form.

12.3.1 Example. We want to ﬁnd the tangent plane to the hyperboloid S deﬁned

at p = ( ,0,2). See Figure 12.6(c).

Solution. Let

fxyz x y z,, .

()

=- + + -

222

-+ + =xyz

222

SpR p=Œ

()

{}

0f.

Figure 12.6. Three quadric surfaces.

Since —f(x,y,z) = (-2x,2y,2z), —f(p) = ( ,0,4) is a normal vector to S at p. It follows

that the tangent plane is deﬁned by

From the point of view of ﬁnding normals to surfaces it is therefore advantageous

to have an implicit representation of it. Unfortunately, except for quadric surfaces,

surfaces are usually presented via parameterizations. Finding an implicit representa-

tion given a parameterization is a nontrivial problem that is addressed in Chapter 10

in [AgoM04].

It should be pointed out that many surfaces of revolution are implicit surfaces, so

that the gradient method for ﬁnding normals and tangent planes applies to them. For

example, consider the surface of revolution deﬁned by equation (12.2). It is easy to

show that this surface is the set of zeros of the function

(12.10)

12.3.2 Example. We rework Example 12.2.4 using this approach. Using equation

(12.10), the surface is deﬁned by the equation

But —F(x,y,z) = (-1,2y,2z) and —F(4,0,2) = (-1,0,4). The latter is, up to a scalar

multiple, the same normal as the one we got before.

Finally, we mention Barr’s ([Barr81]) superquadric surfaces. These are the surface

analogs of superellipses and are useful in representing shapes such as rounded blocks

or rounded square toroids. They are deﬁned by trigonometric functions raised to expo-

nents. [Barr92] presents expressions for their volume, center of mass, and rotational

inertia tensor.

12.4 Ruled Surfaces

Ruled surfaces are probably the next simplest surfaces after planes. Special cases of

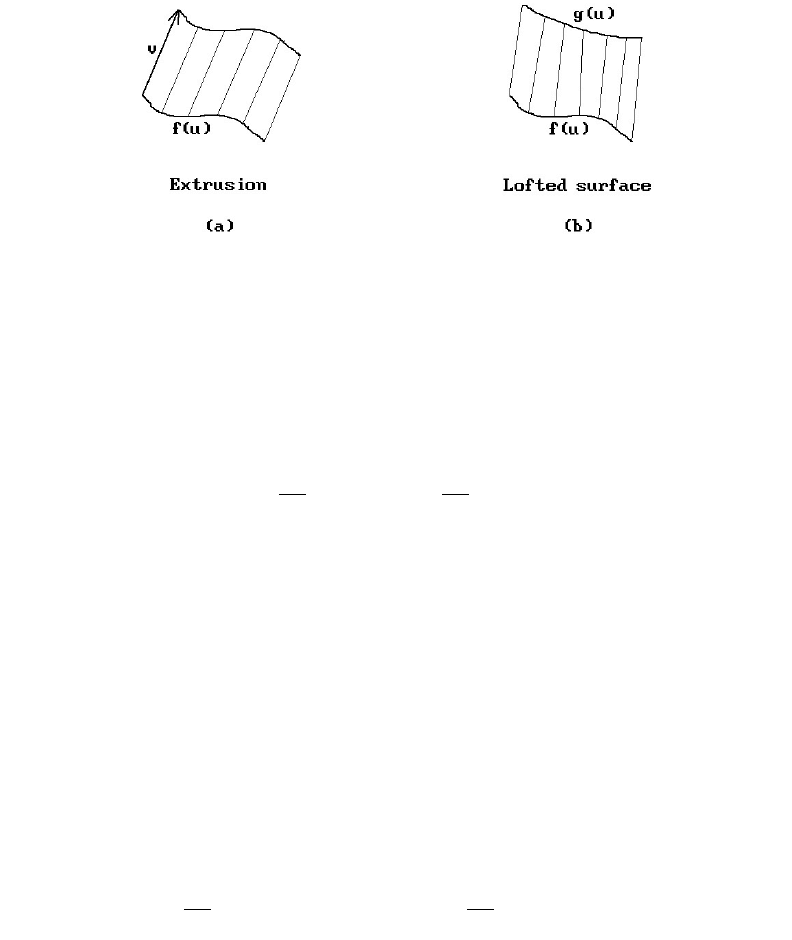
these are extrusions. These are surfaces obtained by sweeping a vector along a curve.

Deﬁnition. Given a curve f : [a,b] Æ R

and a vector v Œ R

, the parametric surface

deﬁned by

pab:, ,

[]

Æ01

Fxyz y z x,, .

()

=+-=

Fxyz y z f x,, .

()

=+-

()

222

-+-=3270xz .

()

∑

()

()()

=2304 302 0,, ,, ,,xyz

-23

482 12 Surfaces in Computer Graphics

12.4 Ruled Surfaces 483

(12.11)

is called an extrusion. The vector v is called the sweep vector for the extrusion.

See Figure 12.7(a). The partials are again easy to compute:

(12.12)

Deﬁnition. Given two curves f, g : [a,b] Æ R

, the parametric surface

deﬁned by

(12.13)

is called a lofted surface.

Lofted surfaces are ruled surfaces that interpolate two curves. See Figure 12.7(b).

The partials are

(12.14)

Note that extrusions are a special case of a lofted surface. In both the case of extru-

sions and the case of lofted surfaces, one needs to worry about self-intersections. Of

the nondegenerate quadric surfaces, the cylinders and cones are ruled surfaces. The

hyperboloid of one sheet and the hyperbolic paraboloid are doubly ruled surfaces. For

a more thorough discussion of ruled surfaces that includes algorithms for computing

planar intersections and contour outlines see [PePR99].

One question that sometimes arises in the context of ruled surfaces is whether

∂

v f u vg u and

gu fu=-

()()

()

1 ¢¢ .

p u v v f u vg u,.

()

()()

()

pab:, ,

[]

Æ01

∂

f u and

()

=¢ v.

put fu t,

()

+ v

Figure 12.7. Extrusions and lofted surfaces.

12.5 Sweep Surfaces 485

Deﬁnition. The parametric surface p(s,t) deﬁned by equation (12.15b) is called the

sweep surface obtained by sweeping f(t) along the framed curve g(s).

12.5.1 Example. The path of a cutter as shown in Figure 12.9(a) can easily be

described as two sweep surfaces deﬁned by equations like equation (12.15b), where

each function f(t) parameterizes a vertical segment.

Equation (12.15b) can be generalized by letting a one-parameter family of

afﬁne maps T

act on the curve f(t) as we sweep it along g(s). Deﬁne function

(s,t) by

and the new parametric surface p(s,t) by

(12.16)

Deﬁnition. The parametric surface p(s,t) deﬁned by equation (12.16) is called a

screw sweep surface.

12.5.2 Example. Let g(s) be the spiral

Using the Frenet frame (T(s),N(s),B(s)) for this curve we let

Let f : [0,4] Æ R

parameterize the unit square in the x–z plane as follows:

110 3 3 1

110 3

sNs s s

sTs s s

sBs s s

()

=- -

()

cos , sin , ,

sin , cos , ,

sin , cos , .

g ssss

()

33cos , sin , .

pst s g st s g st s g st s,,,,.

()

() ()

11 22 33

uuu

T f t g st g st g st

()()

() () ()()

123

,, ,, ,

Figure 12.9. Sweep surfaces: a cutter path and square rotated along a spiral.

486 12 Surfaces in Computer Graphics

We shall rotate the square as it is swept along g(s). This can be accomplished by

deﬁning

The functions g

(s,t) are easily computed. For example, for t Œ [1,2],

Figure 12.9(b) shows the resulting screw sweep surface.

12.6 Bilinear Surfaces

Let four points p

, p

, and p

be given. The easiest way to deﬁne a surface

p(u,v) that interpolates these points is by means of a double linear interpolation.

Deﬁne

(12.17a)

(12.17b)

where 0 £ u, v £ 1. Equation (12.17a) says that to ﬁnd p(u,v) we ﬁrst ﬁnd p(u,0) and

p(u,1) by a linear interpolation in the u-direction and then do a linear interpolation

of those points in the v-direction. Equation (12.17b) says that we get the same answer

if we ﬁrst interpolate in the v-direction and then in the u-direction. See Figure

12.10(a).

Deﬁnition. The parametric surface deﬁned by equations (12.17) is called the

bilinear surface determined by the four points or the four-point interpolating surface.

()

[]

()

[]

()

11 1

11 1 1

00 01 10 11

uv v uv v

uv uv uv uv

pp pp

pppp

puv v u u v u u,,

()

[]

()

[]

11 1

00 10 01 11

pp pp

g s t s g s t and g s t t s

12 3

01, cos , , , , sin .

()

T xyz x syz s

, , cos , , sin .

()

ft t t

()

[]

()

[]

()

[]

()

[]

,, , ,,

,, , , ,

,,, , ,

,, , , .

00 01

10 1 12

301 23

004 34

Figure 12.10. Bilinear surfaces.