Agoston M.K. Computer Graphics and Geometric Modelling: Implementation and Algorithms

Подождите немного. Документ загружается.

2.5 Generating Discrete Curves

Now we start a central topic of this chapter, namely, curves and the problem that one

runs into when one tries to represent them with a discrete set of points. Clearly, we

want any mapping of continuous structures into discrete ones to preserve the visual

shape properties, such as smoothness and uniform thickness, as much as possible but

this is not easy. We shall look at the problem of deﬁning and generating discrete lines

ﬁrst and then conics.

Lines, or more accurately segments, are the most basic of computer graphics

objects because most modeling systems use linear approximations to all objects so

that displaying them reduces to drawing lots of lines. It is possible to actually give a

formal deﬁnition of a discrete “straight” line (see [ArcM75] and [BoLZ75]). Not sur-

prisingly, such deﬁnitions get complicated, but from a practical point of view we are

not really interested in a deﬁnition. Rather, we are happy with an algorithm that gen-

erates a satisfactory set of points for a line. What is satisfactory? Well, that is not very

precise, but some attributes that we want the generated discrete lines to have are:

(1) Visually, the line should appear as straight as possible.

(2) The line should start and end accurately, so that, for example, if several con-

tiguous line segment are drawn, then there is no gap between them.

(3) Each line should appear to have an even visual thickness, that is, it should

have as constant a density as possible, and this thickness should be inde-

pendent of its length and slope.

(4) The conversion process must be fast.

In Sections 2.5.1–2.5.3 we look at line-drawing algorithms for the monochrome

case, that is, where the raster is an array of 0’s and 1’s and the line consists of those

pixels that are set to 1. Section 2.6 looks at some deeper problems that one encoun-

ters in the process of discretizing continuous objects and making them look smooth.

Section 2.9.1 looks at a scan line algorithm for lists of lines and ﬁll algorithm for

polygons.

Conics are the next most common curve after the “straight” line. The circle is one

obvious such curve, but the other conics are also encountered frequently. Their geo-

2.5 Generating Discrete Curves 35

integer

pushrx, pushlx;

pushrx := rx

1; pushlx := lx

Push (lx,rx,pushlx,pushrx,y

dir,dir);

rx > dadRx

then

Push (dadRx

1,rx,pushlx,pushrx,y

dir,dir);

lx < dadLx

then

Push (lx,dadLx

1,pushlx,pushrx,y

dir,dir);

end;

Algorithm 2.4.3. Continued

metric properties and relatively low degree (when compared with the popular cubic

splines) make them attractive for use in designing shapes such as fonts. Because of

this, a great deal of effort has been spent on devising efﬁcient algorithms for com-

puting them. We shall look at a few of these in Sections 2.9.2 and 2.9.3.

Because one common theme of some of the algorithms that generate discrete

curves is derived from the geometric approach to solving differential equations, we

start with that subject.

2.5.1 Digital Differential Analyzers

Consider the basic ﬁrst order differential equation of the form

(2.1)

If y(x) is any solution, then f(x,y(x)) speciﬁes the slope of the graph of y(x) at the point

(x,y(x)). In other words, if one thinks of the function f as specifying a vector ﬁeld over

the entire plane (to (x,y) in the plane we associate the vector (1,f(x,y))), then solving

equation (2.1) corresponds to ﬁnding a parameterized curve x Æ (x,y(x)) whose

tangent vectors agree with the vectors from this vector ﬁeld. Mathematicians call such

curves “integral curves.” In general, given a vector ﬁeld, a curve whose tangent vectors

agree with the vectors of that vector ﬁeld at every point on the curve is called an inte-

gral curve for that vector ﬁeld. See Figure 2.7. The reason for this nomenclature is

that solving for the curve basically involves an integration process.

This idea of vector ﬁelds and integral curves leads to the following approach to

ﬁnding numerical solutions to differential equations called Euler’s method. Suppose

that we want the solution to pass through p

= (x

). Since we know the tangent

vector to the solution curve there and since the tangent line is a good approximation

to the curve, moving a small distance along the tangent, say by e(h(x

),g(x

)),

where e is a small positive constant, will put us at a point p

= (x

), which hope-

fully is not too far away from an actual point on the curve. Next, starting at p

repeat this process. In general, let

fxy

gxy

hxy

()

36 2 Raster Algorithms

Figure 2.7. Integral curves of a vector

ﬁeld.

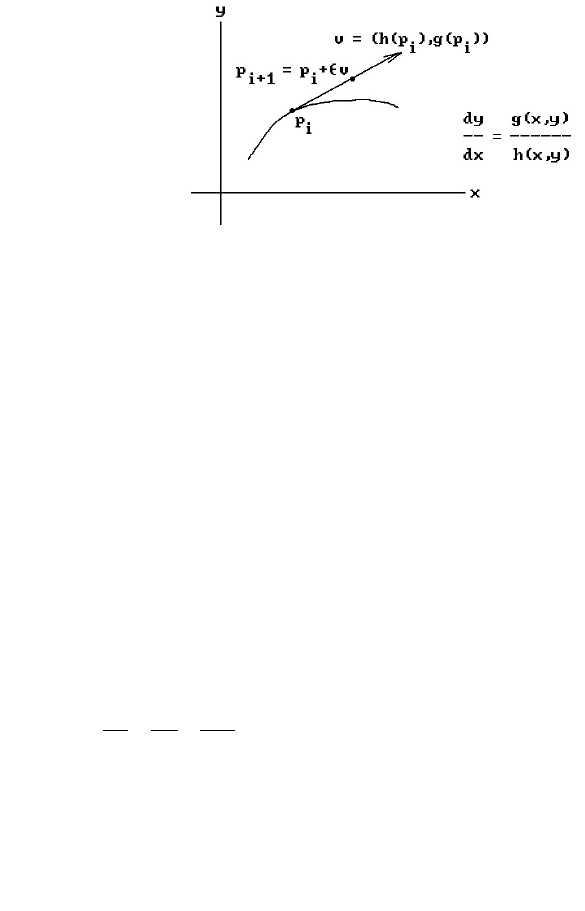
(2.2)

See Figure 2.8. The sequence of points p

, p

, ..., p

obtained in this way becomes

our approximation to the actual integral curve passing through p

Unfortunately, as we move from point to point we start drifting away from the

actual curve and so our approximation will, in general, get further and further away

from the true solution. To make the method work we need to compensate for any

possible error as we move along. There are some very good algorithms that solve dif-

ferential equations with basically this approach by using some fancy error-correcting

terms. For more information see a text on numerical analysis such as [ConD72] or

[DahB74].

Discrete curve-drawing algorithms that are based on the qualitative solutions to

differential equations as described above are called digital differential analyzer or DDA

type algorithms. Let us see what we get in the special case of straight lines.

The differential equation for the straight line that passes through the points (x

)

and (x

) is

where Dy = y

- y

, Dx = x

- x

, and e is any positive real number. Specializing the

approximation formula, equation (2.2), to this differential equation gives us a

sequence of points p

deﬁned by

(2.3)

In fact, the points p

we generate will actually fall on the line, so that we do not have

to worry about compensating for any errors. Although this may seem like overkill in

the case of continuous lines, it does motivate an approach to generating discrete lines

that leads to an extremely efﬁcient such algorithm (the Bresenham algorithm). Note

that if q

is the point with integer coordinates that is gotten from p

by rounding each

real coordinate of p

to its nearest integer, then the points q

deﬁne a discrete curve

that is an approximation to the continuous one. The key to getting an efﬁcient line-

drawing algorithm is to be able to compute the q

efﬁciently.

()

eeDD,.

i i ii ii

hx y gx y

()()()

e ,, , .

2.5 Generating Discrete Curves 37

Figure 2.8. Generating an integral curve

approximation.

In the continuous case one always generates points on the line no matter what e

is chosen but the choice of e does matter when generating discrete lines. We now look

at two possible choices for e. These give rise to what are called the simple and sym-

metric DDA, respectively.

Let m = max(|Dx|,|Dy|).

The simple DDA: Choose e=1/m.

The symmetric DDA: Choose e=2

-n

, where 2

n-1

£ m < 2

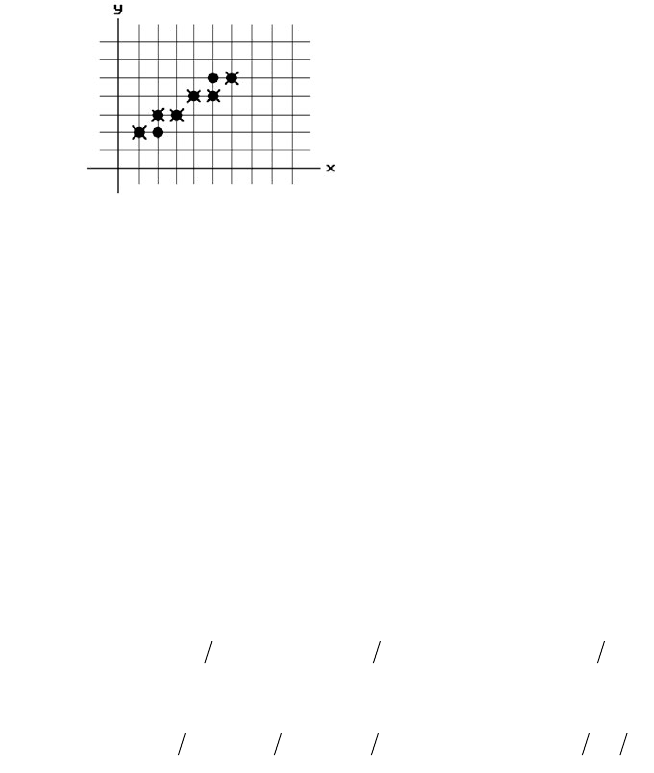
2.5.1.1 Example. Suppose that we want to generate the discrete line from (1,2) to

(6,5).

Solution. In this case (Dx,Dy) = (5,3). For the simple DDA we have

In the case of the symmetric DDA, we have

The points that are generated are shown in Figure 2.9. The points of the simple DDA

are shown as ¥¢s and those of the symmetric DDA are shown as solid circles.

2.5.2 The Bresenham Line-Drawing Algorithm

Although the DDA algorithms for drawing straight lines are simple, they involve real

arithmetic. Some simple modiﬁcations result in an algorithm that does only integer

arithmetic, and only additions at that.

Note that in the case of the simple DDA, either x or y will always be incremented

by 1. For simplicity, assume that the start point of our line is the origin. If we also

restrict ourselves to lines whose endpoint is in the ﬁrst octant in the plane, then it will

be the x that always increases by 1. Therefore, we only need to worry about comput-

ing the y coordinates efﬁciently.

ee e=== =+

()

18 58 38 5838

,,, ,.DDx y and

eee=== =+

()

15 1 35 135

,, , ,.DDx y and

38 2 Raster Algorithms

simple DDA ∑ symmetric DDA

Figure 2.9. Simple and symmetric

DDA generated lines.

Suppose therefore that we want to draw a line from (0,0) to (a,b), where a and b

are integers and 0 £ b £ a (which puts (a,b) into the ﬁrst octant). Using equation (2.3),

the points p

, 0 £ i £ a, generated by the simple DDA are then deﬁned by

and the discrete line consists of the points (i,y

), where y

is the real number i(a/b)

rounded to the nearest integer.

Now the y coordinates start at 0. At what point does y

become 1? To answer this

question, we must compute b/a, 2b/a, 3b/a, ..., and watch for that place where these

values become bigger than 1/2. Furthermore, the y

will then stay 1 until these values

become bigger than 3/2, at which time y

will become 2. Since we want to avoid doing

real arithmetic, note that we do not really care what the actual values are but only

care about when they get bigger than 1/2, 3/2, 5/2, .... This means that we can mul-

tiply through by 2a and the answer to the question as to when y

increases by 1 is

determined by when 2b, 4b, 6b, . . . become bigger than a, 3a, 5a, .... Since comput-

ers can compare a number to 0 in less time than it takes to compare it to some other

number, we shall start off by subtracting a. Our ﬁrst question now is

“When does 2b - a, 4b - a, 6b - a, . . . become bigger than 0?”

and only involves repeated integer additions of 2b to an initial sum d = 2b - a. After

the sum d has become bigger than 0 and y has switched to 1, we need to check when

the sum becomes bigger than 2a. By subtracting 2a, we again only need to keep check-

ing for when the sum gets to be bigger than 0 by successive additions of 2b. In general,

whenever y is incremented by 1, we subtract 2a from the current sum d. In that way

we always need to check d simply against 0. For example, suppose we want to draw

the line from (0,0) to (15,3). In this case, 2a = 30, 2b = 6, and the initial d is 6 - 15 =

-9. The table below shows the points (x

) that are drawn and the changes to the

sum d as i ranges from 0 to 8:

i 012345678

d -9 -3 -27 -21 -15 -9 -3 -27

) (0,0) (1,0) (2,0) (3,1) (4,1) (5,1) (6,1) (7,1) (8,2)

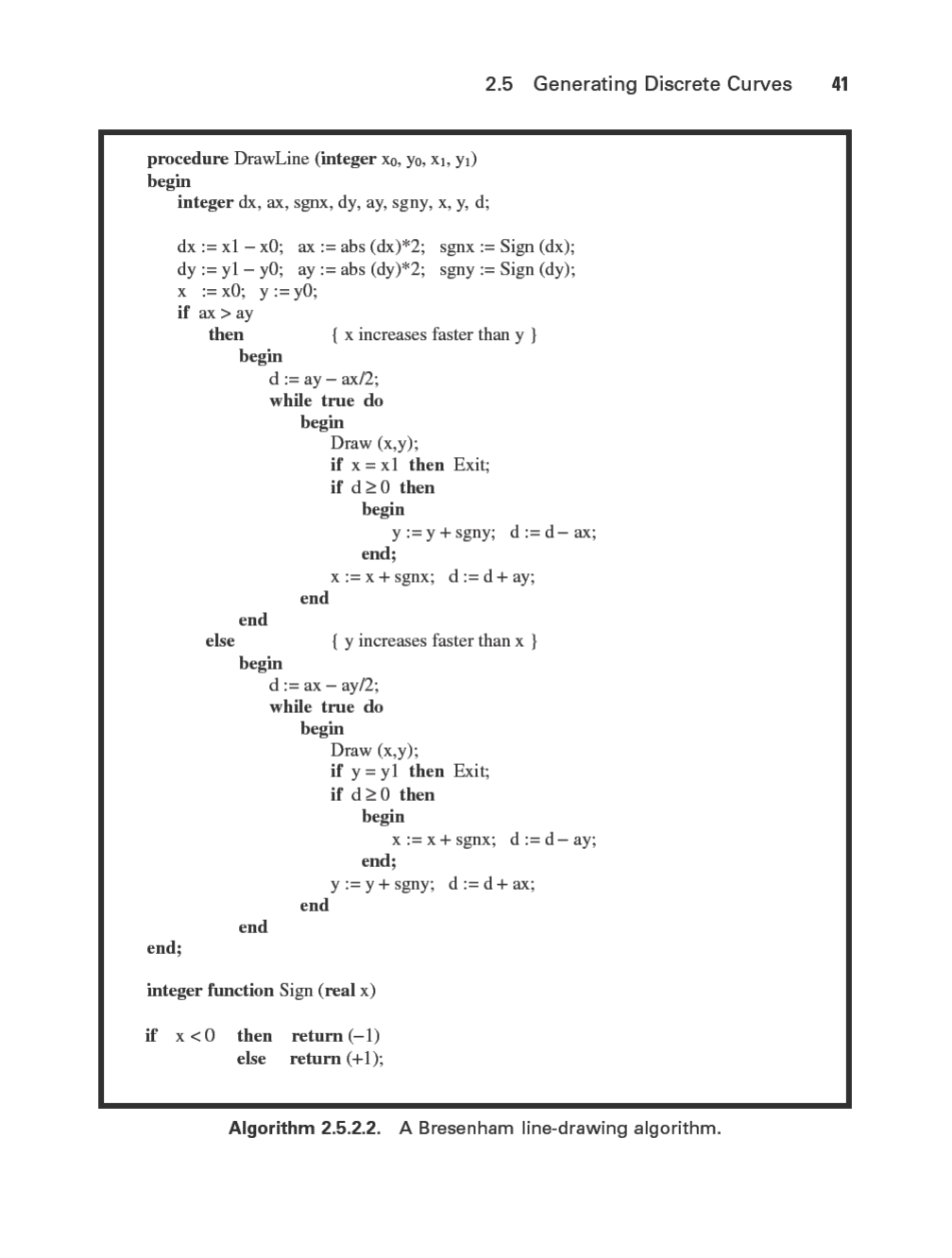
The code in Algorithm 2.5.2.1 implements the algorithm we have been describing.

In our discussion above we have restricted ourselves to lines that start at the origin

and end in the ﬁrst octant. Starting at another point simply amounts to adding a con-

stant offset to all the points. Lines that end in a different octant can be handled in a

similar way to the ﬁrst octant case – basically by interchanging the x and y. What this

boils down to is that an algorithm which handles all lines is not much harder, involv-

ing only a case statement to separate between the case where the absolute value of

the slope is either larger or less than or equal to 1.

We have just described the basis for the Bresenham line-drawing algorithm

([Bres65]). It, or some variation of it, is the algorithm that is usually used for drawing

straight lines. Bresenham showed in [Bres77] that his algorithm generated the best-

ﬁt discrete approximation to a continuous line. The variation that is Algorithm 2.5.2.2

ba iiba=+

()

-1

1, , ,

2.5 Generating Discrete Curves 39

comes from [Heck90c] and works for all lines. It generates the same points as the

original Bresenham line-drawing algorithm but is slightly more efﬁcient.

To further improve the efﬁciency of DDA-based algorithms, there are n-step algo-

rithms that compute several pixels of a line at a time. The ﬁrst of these was based on

the idea of double stepping. See [RoWW90] or [Wyvi90]. There are also algorithms

that use a 3- or 4-step process. See [BoyB00] for an n-step algorithm that automati-

cally uses the optimal n and claims to be at least twice as fast as earlier ones.

2.5.3 The Midpoint Line-Drawing Algorithm

Because drawing lines efﬁciently is so important to graphics, one is always on the

lookout for better algorithms. Another well-known line-drawing algorithm is the so-

called midpoint line-drawing algorithm. It produces the same pixels as the Bresenham

algorithm, but is better suited for generalizing to other implicitly deﬁned curves such

as conics and also to lines in three dimensions (see Section 10.4.1). The general idea

was ﬁrst described in [Pitt67] and is discussed in greater detail by [VanN85].

Assume that a nonvertical line L is deﬁned by an equation of the form

fxy ax by c,,

()

=++=0

40 2 Raster Algorithms

Code for drawing the discrete line from (0,0) to the point (a,b) in the first octant:

begin

integer d, x, y;

d := 2*b - a;

x := 0;

y := 0;

while true do

begin

Draw (x,y);

if x = a then Exit;

if d ≥ 0 then

begin

y := y + 1;

d := d - 2*a;

end;

x := x + 1;

d := d + 2*b;

end

Algorithm 2.5.2.1. Basic line-drawing algorithm.

where -b ≥ a ≥ 0. This assumption implies that our line has slope between 0 and 1.

Lines with other slopes are handled in a symmetric way like in Bresenham’s algo-

rithm. Vertical lines are a very special case that would be handled separately. Another

important consequence of our assumptions is that f(x,y) will be positive for points

(x,y) below the line and negative for points above the line. Also like in the Bresenham

algorithm, the points p

= (x

) that we will generate for the line will have the prop-

erty that the x-coordinate will be incremented by 1 each time, x

i+1

= x

+ 1, so that we

only have to determine the change in the y coordinate.

See Figure 2.10. The only possible value for y

i+1

is y

or y

+ 1. The decision will

be based on the sign of

If d

> 0, then the line L crosses the line x = x

+ 1 above the point (x

+ 1, y

+ 0.5) and

we need to let y

i+1

be y

+ 1. If d

< 0, then we should let y

i+1

be y

. If d

= 0, then either

y value would be satisfactory. We shall choose y

in that case. Choosing our points p

in this way is what constitutes the basic idea behind the midpoint line-drawing algo-

rithm. The only thing that is left is to describe some optimizations that can be made

in the computations. First, the d

can be computed efﬁciently in an incremental way.

By deﬁnition, if d

£ 0, then

On the other hand, if d

> 0, then

This shows that the next value of the decision variable can be computed by simple

additions to the previous value. If our line L starts at the point p

= (x

) , then

This gives us the starting value for the decision variable and all the rest are computed

incrementally. We can avoid the fraction in the starting value and do all our compu-

dfx y fxy ab

000 00

105 2=++

()

++,. , .

dfx y

ax by c

dab

iii

=+ +

()

=++

215

dfx y

ax by c

iii

=+ +

()

205

dfx y

iii

=++

()

105,..

42 2 Raster Algorithms

Figure 2.10. The midpoint line-drawing algorithm

decision.

tations using purely integer arithmetic by multiplying the equation for our line by 2,

that is, let us use

This has the effect of multiplying our starting value for the decision variable and its

increments by 2. Since only the sign of the variable was important and not its value,

we have lost nothing. Putting all this together leads to Algorithm 2.5.3.1.

Finally, before leaving the subject of line-drawing algorithms, we should point out

that there are other such algorithms other than the ones mentioned here. For example,

there are run-based line drawing algorithms. See [SteL00]. One thing to keep in mind

F x y f x y ax by c,, .

()

=++

()

=22 0

2.5 Generating Discrete Curves 43

procedure

DrawLine

(integer

, y

, x

, y

)

{ We have chosen the equation

f (x, y) = (dy) x

(dx) y

c = 0

as the equation for the line.}

begin

integer

dx, dy, d, posInc, negInc, x, y;

dx := x

;

dy := y

;

d := 2*dy

dx; { Initial value of decision variable }

posInc := 2*dy; { The increment for d when d

≥

0 }

negInc := 2*(dy

dx); { The increment for d when d < 0 }

x := x

; y := y

;

Draw (x,y);

while

x < x

begin

then d := d

posInc

else

begin

d := d

negInc;

y := y

end

;

x := x + 1;

Draw (x,y);

end

end;

Algorithm 2.5.3.1. The midpoint-line drawing algorithm.

though is that the time spent in line drawing algorithms is often dominated by the

operation of setting pixels in the frame buffer, so that software improvements alone

may be less important.

2.6 The Aliasing Problem

No matter how good a line drawing algorithm is, it is impossible to avoid giving most

discrete lines a staircase effect (the “jaggies”). They just will not look “straight.”

Increasing the resolution of the raster helps but does not resolve the problem entirely.

In order to draw the best looking straight lines one has to ﬁrst understand the “real”

underlying problem which is one of sampling.

The geometric curves and surfaces one is typically trying to display are continu-

ous and consist of an inﬁnite number of points. Since a computer can only show a

ﬁnite (discrete) set of points, how one chooses this ﬁnite set that is to represent the

object is clearly important. Consider the sinusoidal curve in Figure 2.11. If we sample

such a sine wave badly, say at the points A, B, C, and D, then it will look like a straight

line. If we had sampled at the points A, E, F, and D, then we would think that it has

a different frequency.

The basic problem in sampling theory: How many samples does one have to take so

that no information is lost?

This is a question that is studied in the ﬁeld of signal processing. The theory of

the Fourier transform plays a big role in the analysis. Chapter 21, in particular Section

21.6, gives an overview of some of the relevant mathematics. For more details of the

mathematics involved in answering the sampling problem see [GonW87], [RosK76],

or [Glas95]. We shall only summarize a few of the main ﬁndings here and indicate

some practical solutions that are consequences of the theory.

Deﬁnition. A function whose Fourier transform vanishes outside a ﬁnite interval is

called a band-limited function.

One of the basic theorems in sampling theory is the following:

The Whittaker-Shannon Sampling Theorem. Let f(x) be a band-limited function

and assume that its Fourier transform vanishes outside [-w,w]. Then f(x) can be

reconstructed exactly from its samples provided that the sampling interval is no bigger

than 1/(2w).

44 2 Raster Algorithms

Figure 2.11. Aliasing caused by bad sampling.