Agoston M.K. Computer Graphics and Geometric Modelling: Implementation and Algorithms

Подождите немного. Документ загружается.

with angles close to p are often undesirable and a lot of work has been done to get

more nicely shaped triangles in the end. As one example, we mention the paper

[BeMR94] that describes a way to get a triangulation so that no angle in the triangles

is larger than p/2. It starts by ﬁrst packing the polygon with disks.

Finally, the triangulation algorithm we described above also applies to polygons

with holes and, more generally, for arbitrary planar subdivisions. For polygons with

holes see also the trapezoidation algorithm in Section 14.4 and [ZalC99].

17.6 Triangulating Polygons 719

Inputs:

A strictly y-monotone polygon

specified by two chains of vertices

starting at the top vertex with one chain listing the vertices along the

right side of the polygon and the other listing the ones on the left

Outputs:

A triangulation of

as an appropriately specified list of edges T

tagged vertex p

;

stack of tagged vertices

integer

Order the vertices of

by decreasing y-coordinate with vertices having the same

y-coordinate being ordered by increasing x-coordinate. Let

be the

vertices listed in that order tagged by whether they are on the right or left side of

Initialize S to empty; Add all edges of

to T;

Push (

,S); Push (

,S);

for

i:=3

if p

and Top (S) lie on different sides of the polygon

then

begin

while

|S| > 1

begin

:= Pop (S); Insert a diagonal from

into T;

end

Pop (S); Push (

,S); Push (

,S);

end

else

begin

:= Pop (S);

while

diagonal from

to Top (S) lies in

Pdo

begin

:= Pop (S); Insert a diagonal from

into T;

end

;

Push (

,S);

end

;

Insert into T a diagonal from

to all the vertices on S except the first and last;

Algorithm 17.6.1. The triangulation algorithm for y-monotone polygons.

17.7 Voronoi Diagrams

Voronoi diagrams are structures that get used in many places in geometric modeling

and computational geometry. This section will deﬁne them and summarize some of

their more important properties. Some good references for more information about

them are [Aure91], [BKOS97], [PreS85], and [Edel87].

The general problem that Voronoi diagrams address is:

For each point p in a given a set S of points of a space X, ﬁnd all the points of X that are

closest to p.

We make this more precise. We shall only consider Voronoi diagrams for the plane,

that is, the case X = R

. This is the case that one encounters most often. At the end

of the section we shall make some comments about other cases.

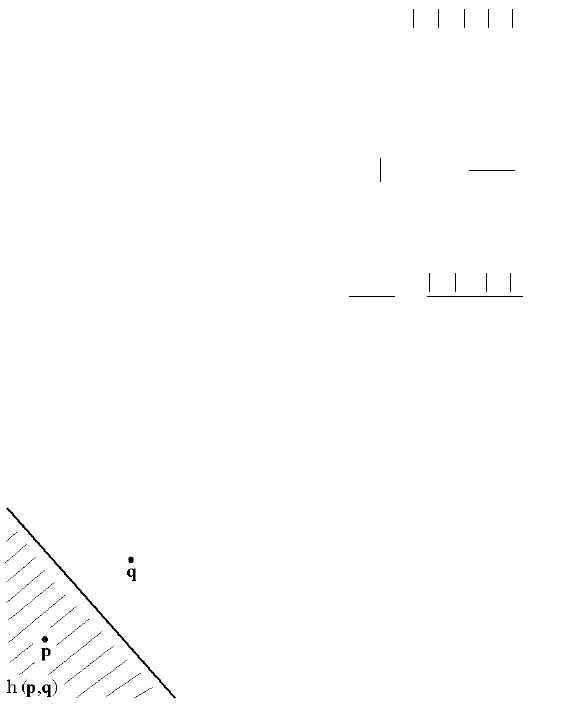
Deﬁnition. Let p, q Œ R

, p π q. Deﬁne the halfplane h(p,q) by

It is easy to show that h(p,q) actually is a halfplane. See Figure 17.13. In fact, it

is the halfplane containing p determined by the perpendicular bisector of the segment

[p,q], that is,

This fact follows easily from the identity

Now let S be a ﬁnite set of points in R

. The elements of S will be called sites.

Deﬁnition. The Voronoi cell of a point p in S, denoted by V(p), is deﬁned by

Vhpp,q

qS p

()

Œ-

{}

pq r

p q pr rq

•.-

h p q r R pq r

,•.

()

=Œ -

h p q r R pr rq,.

()

=Œ £

{}

720 17 Computational Geometry Topics

Figure 17.13. A halfplane h(p,q).

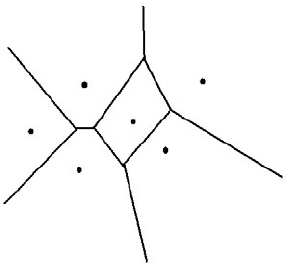
Figure 17.14 shows a Voronoi diagram for six sites. Here are a few basic facts

about the sets V(p):

17.7.1 Proposition. Let S be a ﬁnite set of n points in the plane.

(1) Each V(p) is a nonempty convex set because it is an intersection of (convex)

halfplanes that contain p. It has a nonempty interior because it contains a small neigh-

borhood about p consisting of points that belong to no other Voronoi cell.

(2) The boundary of each V(p) is the union of at most n - 1 segments or halﬂines,

called the edges of V(p). (We assume that an edge is a maximal linear subset of the

boundary, that is, the lines determined by the edges are distinct, or, alternatively, no

two edges lie in the intersection of the same pair of Voronoi cells.) The boundary has

at most n - 1 vertices, where a vertex is the intersection of two edges.

(3) Each point in the interior of an edge of a V(p) is equidistant to precisely two

sites. Each vertex is equidistant to at least three sites.

(4) If p π q, then V(p) « V(q) is either empty or consists of a single edge.

(5) Every point of the plane belongs to at least one Voronoi cell V(p).

Proof. Easy. See [Aure91] or [BKOS97].

Deﬁnition. The Voronoi diagram of the set S, denoted by Vor(S), is the set of Voronoi

cells V(p), p Œ S, together with their edges and vertices.

Proposition 17.7.1(4) and (5) imply that Vor(S) deﬁnes a kind of partition of the

plane. The only reason that we cannot call it a cell complex is that it contains

unbounded sets that are homeomorphic to half-open disks. (Cell complexes are deﬁned

in Section 7.2.4 in [AgoM05]. Their cells must be homeomorphic to closed disks.)

Deﬁnition. Given a point p, let C

(p) denote the largest circle centered at p that con-

tains no site of S in its interior.

17.7.2 Proposition. Let S be a ﬁnite set of n points in the plane.

(1) Vor(S) contains precisely n “2-cells.”

(2) The Voronoi diagram contains no vertices if and only if all sites are collinear.

17.7 Voronoi Diagrams 721

Figure 17.14. A Voronoi diagram.

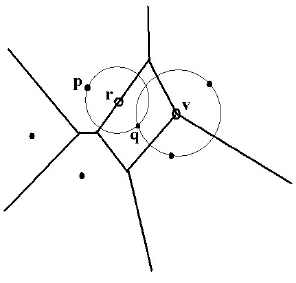
(3) A point v is a vertex of Vor(S) if and only if C

(v) passes through at least three

sites in S. See Figure 17.15.

(4) Two Voronoi cells V(p) and V(q) determine an edge of Vor(S) if and only if

there is a point r so that C

(r) contains p and q in its boundary but no other site. See

Figure 17.15.

(5) If no four points of S lie on a circle, then every vertex of Vor(S) belongs to

precisely three edges of Vor(S).

(6) Vor(S) contains at most 3n - 6 edges and at most 2n - 5 vertices.

Proof. See [BKOS97]. (3) and (4) characterize the vertices and edges of Vor(S).

Next, we consider the question of how to compute the Voronoi diagram for n sites

efﬁciently. Because the problem of sorting n numbers can be reduced to computing a

Voronoi diagram, one should not expect any algorithm to be faster than O(nlog n).

Fortune’s algorithm ([Fort87]) is an algorithm that achieves this best complexity.

17.7.3 Theorem. The Voronoi diagram of a set of n points in the plane can be

computed in time O(nlogn) using O(n) space.

Proof. See [BKOS97].

Voronoi diagrams can be generalized to higher dimensions. It has been shown

that Voronoi diagrams for n sites in R

can be computed in O(nlogn + n

Èm/2˘

) optimal

time. The important special case of Voronoi diagrams for three-dimensional linear

polyhedra has been studied extensively. A recent algorithm and implementation is

described in [EtzR99]. It separates the problem into two parts. First, a symbolic rep-

resentation called the Voronoi graph is computed and then the geometric part, namely,

the actual vertices and edges.

17.8 Delaunay Triangulations

Closely related to Voronoi diagrams are Delaunay triangulations. Again we shall

restrict ourselves to subsets of the plane.

722 17 Computational Geometry Topics

Figure 17.15. Characterizing vertices and edges of a

Voronoi diagram.

Deﬁnition. Let S be a ﬁnite set of points (sites) in the plane. The Delaunay graph

of S is the graph with vertex set S and whose edges are deﬁned by the condition that

two vertices are connected by an edge if and only if the Voronoi cells associated

to those vertices share a common edge. The Delaunay cell complex of S is the two-

dimensional cell complex deﬁned by the condition that its vertices and edges are the

vertices and edges of the Delaunay graph of S. The 2-cells are called the faces of the

Delaunay cell complex. By subdividing the faces of the Delaunay cell complex into tri-

angles, if they are not that already, one obtains a two-dimensional simplicial complex

called a Delaunay triangulation of S.

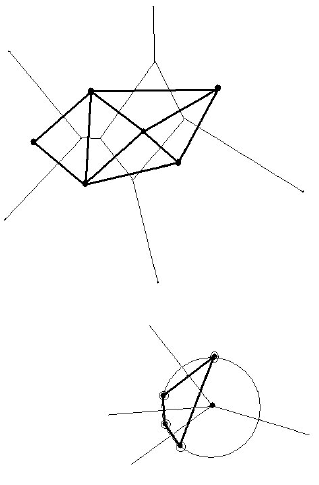
Figure 17.16 shows the Delaunay cell complex associated to the Voronoi diagram

in Figure 17.14. As we can see, it is in fact a Delaunay triangulation. Figure 17.17

shows a Delaunay cell complex deﬁned by the four sites marked by circles. It consists

of a single face that is a quadrilateral and not a triangle. It admits two Delaunay

triangulations. Now, the fact that we always do get a real cell complex needs some

justiﬁcation, which is provided by the properties of the Delaunay graph listed in the

following theorem.

17.8.1 Theorem. The Delaunay graph for a set S satisﬁes the following properties:

(1) The Delaunay graph G is the “dual graph” of the Voronoi diagram D in the

sense that a Voronoi cell in D becomes a vertex in G, an edge e in D deﬁnes an edge

in G between the two vertices in G that correspond to the Voronoi cells that have e

in common, and a vertex v in D deﬁnes the (triangular) region bounded by edges of

G which connect the Voronoi cells that have v in common. (Compare this to the

barycentric subdivision of a simplicial complex.)

17.8 Delaunay Triangulations 723

Figure 17.16. A Delaunay triangulation.

Figure 17.17. A nontriangular face of a Delaunay cell complex.

(2) An edge is orthogonal to the edge the Voronoi cells share but does not neces-

sarily intersect that edge.

(3) A Delaunay graph of a planar set is a planar graph.

(4) If no four points of S lie on a circle, then each face of the Delaunay cell

complex is a triangle.

(5) Three points of S are vertices of the same face of the Delaunay cell complex

if and only if the circle deﬁned by them contains no point of S in its interior.

(6) Two points of S deﬁne an edge in the Delaunay graph if and only if there is a

closed disk that contains those points in its boundary and which contains no other

points of S.

(7) A Delaunay triangulation contains at most 3n - 6 edges and 2n - 4 faces.

Proof. See [Aure91] or [BKOS97]. Parts (5), (6), and (7) follow from Theorem

17.7.2(3), (4), and (6).

Deﬁnition. Let S be a ﬁnite set of points in R

. A triangulation of S is a simplicial

complex K whose vertex set is S and whose underlying space is the convex hull of S.

17.8.2 Theorem. Let S be a ﬁnite set of points in the plane and let K be a trian-

gulation of S. Then K is the Delaunay triangulation of S if and only if the circle cir-

cumscribing any triangle in K does not contain any point of S in its interior.

Proof. The theorem is an easy consequence of Theorem 17.8.1(5) and (6).

One of the important uses of Delaunay triangulations is to ﬁnd a triangulation

of the convex hull of a set of points with the property that the triangles have as good

a shape as possible. For example, long thin triangles are undesirable in many

applications.

Deﬁnition. Let S be a ﬁnite set of points in the plane and let K be a triangulation

of S. If K has m triangles and if we order the 3m angles q

of these triangles in increas-

ing order so that q

£q

if i < j, then the vector (q

,...,q

) is called an angle vector

of K. The triangulation K is called angle-optimal for S if (q

,...,q

) ≥ (t

,...,

) for all angle vectors (t

,...,t

) of triangulations of S.

17.8.3 Theorem. Let S be a ﬁnite set of points in the plane.

(1) Any angle-optimal triangulation of S is a Delaunay triangulation of S.

(2) Any Delaunay triangulation of S maximizes the minimal angle of the trian-

gles in any triangulation of S. If no four points of S lie on a circle, then the Delaunay

triangulation of S is angle-optimal.

Proof. See [BKOS97].

The property in Theorem 17.8.3(2) can be expressed in another way. Note that

there are two ways that a quadrilateral can be triangulated because we can choose

either of the two diagonals. Given a triangulation, consider quadrilaterals that consist

of two adjacent triangles in that triangulation. A Delaunay triangulation has the

724 17 Computational Geometry Topics

property that, for all such quadrilaterals, the minimum of the six angles in the two

triangles that triangulate it will not increase if one switches to the other triangulation

and replaces the diagonal that is the common edge by the other diagonal. Although

Delaunay triangulations maximize the minimal angle of triangles, it is easy to give

examples that it does not minimize the maximal angle.

17.8.4 Theorem. Using a Voronoi diagram a Delaunay triangulation can be com-

puted in O(n) time after a precomputation time of the Voronoi diagram of O(nlog n).

Proof. See [Aure91] or [BKOS97].

Rather than computing a Delaunay triangulation from a Voronoi diagram, which

involves computing and storing the vertices of that diagram, there are algorithms that

compute it directly. The three main approaches are divide-and-conquer ([GuiS85] and

[Dwye87]), sweepline ([Fort87]), and incremental ([GreS77], [ClaS89], [BDST92],

[FanP93], [BoiT93], [Lisc94], [BKOS97], [Devi98]). According to tests described in

[SuDr95] and [Shew96] the divide-and-conquer algorithms seem to be the fastest with

the sweepline algorithms the next fastest and the incremental algorithms the slowest,

although the simplest. An algorithm based on the divide-and-conquer approach that

also extends to higher dimensions can be found in [CiMS98].

Finally, if one wants to generalize to higher dimensions, one can build on what is

known for Voronoi diagrams in that case or again try to deal with the problem directly.

For a survey of this topic see [Aure91]. A speciﬁc implementation for a Delaunay tri-

angulation for three dimensions can be found in [FanP95].

17.8 Delaunay Triangulations 725

18.2 Basic Deﬁnitions

Deﬁnition. Let I(R) denote the set of closed intervals in R.

By identifying the real number a with the interval [a,a] we shall consider R

as a subset of I(R). Throughout this chapter we shall use capital letters to denote

intervals.

Deﬁnition. If A = [a,b] Œ I(R), then deﬁne

Next, here are the basic arithmetic operators of addition, subtraction, multipli-

cation, and division on intervals.

Deﬁnition. Let

Œ {+, -, ◊, /}. Let A, B Œ I(R). Deﬁne

In the case of /, we shall always assume that 0 does not belong to B. At times we shall

abbreviate the product A◊B to AB.

18.2.1 Lemma. If A = [a,b] and B = [c,d], then the following holds:

(1) A + B = [a + c,b + d]

(2) A◊B = [min(ac,ad,bc,bd), max(ac,ad,bc,bd)]

(3) A - B = [a - d,b - c] = A + [-1,-1]◊B

(4) A / B = [min(a/c,a/d,b/c,b/d), max(a/c,a/d,b/c,b/d)]

= [a,b]◊[1/d,1/c]

Proof. This is an easy exercise.

18.2.2 Examples. [-1,3] + [2,5] = [1,8]

[-1,3] - [2,5] = [-6,1]

[-1,3]◊[2,5] = [-5,15]

[-1,3] / [2,5] = [-1/2,3/2]

The next lemma summarizes some basic facts that, among other things, show that

the operations on I(R) act very much like they do on the reals R. The main fact that

keeps (I(R), +, ◊) from being a ring is that is does not have additive inverses.

18.2.3 Lemma. Let A, B, C, D Œ I(R). Then

(1) (Commutativity) A + B = B + A and A◊B = B◊A.

(2) (Associativity) (A + B) + C = A + (B + C) and (A◊B)◊C = A◊(B ◊C).

(3) (Identity) The intervals [0,0] and [1,1] are the unique additive and multi-

plicative identities, respectively. More precisely,

A B a b a A and b B

=Œ Œ

{}

lb A a and ub A b

()

=,.

18.2 Basic Deﬁnitions 727

728 18 Interval Analysis

(4) I(R) has no zero divisors.

(5) The only elements [a,b] in I(R) that have an additive or multiplicative inverse

are those for which a = b. However, we do have

(6) A◊(B + C) + A◊B + A◊C (subdistributivity)

a◊(B + C) = a◊B + a◊C, a Œ R

A◊(B + C) = A◊B + A◊C if bc ≥ 0 for all b Œ B and c Œ C

(7) If A Õ C and B Õ D, then A

B Õ C

D, for

Œ {+, -, ◊, /}. This is often expressed

by saying that the standard interval arithmetic operators are inclusion isotone or inclu-

sion monotonic.

Proof. This is fairly straightforward. See [AleH83].

18.2.4 Example. The distributive law fails:

Property (7) in Lemma 18.2.3 is particularly important. In the context of compu-

tations, it tells us that as new errors creep into computations we can keep control of

them.

It is possible to deﬁne a metric on I(R).

Deﬁnition. Deﬁne

18.2.5 Lemma. The function d deﬁnes a metric on I(R).

Proof. This is easy to show directly, but actually it is the well-known Hausdorff

metric.

18.2.6 Example. d([-1,3],[2,5]) = max(|-1 - 2|,|3 - 5|) = 3.

18.2.7 Theorem.

(1) (I(R), d) is a complete metric space.

(2) The operations of addition, subtraction, multiplication, and division deﬁned

on I(R) are continuous.

dab cd a c b d, , , max , .

[][]

()

=--

()

dI I: RRR

()

12 11 1 1 00 12 11 12 1 1 11,, , , ,,, , ,.

[]

◊

()

+- -

()

[]

[] []

◊

[]

◊- -

[]

but

01Œ- Œ Œ

()

A A and A A Ifor all A R .

AXAAX

AYAAY

=+=+

()

[]

=◊=◊

()

[]

for all X in I if and only if X

for all Y in I if and only if Y