Agoston M.K. Computer Graphics and Geometric Modelling: Implementation and Algorithms

Подождите немного. Документ загружается.

some of whose parameter data ﬁelds are described in Figure C.7. In particular,

for

and

The coefﬁcients D or the coefﬁcients D and C will be zero if the polynomials are of

degree 2 or 1, respectively. If the curve is planar, then the Z coefﬁcients will be zero,

except that AZ(i) will specify the plane z = AZ(i) that contains the curve. So that one

can get the value and the ﬁrst, second, and third derivative at the end point of the

curve without computing the polynomial at u = T(N + 1), these values, divided by

appropriate factorials, are included in the parameter data at the end of the coefﬁcient

data. The entity in our example has its data in parameter data lines 41 through 53.

We see that

suTi=-

()

Ti u Ti i N

()

££ +

()

=112, , ,..., ,

x u AX i BX i s CX i s DX i s

y u AY i BY i s CY i s DY i s

z u AZ i BZ i s CZ i s DZ i s

()

C.3 The IGES Geometric Types 829

Parameter Name Type Description

ææææææææææææææææææææææææææææææææ

1 zt Real Parallel zt displacement of arc from xt, yt plane

2 x1 Real Arc center x-coordinate

3 y1 Real Arc center y-coordinate

4 x2 Real Start point x-coordinate

5 y2 Real Start point y-coordinate

6 x3 Real Terminate point x-coordinate

7 y3 Real Terminate point y-coordinate

8 n Integer Number of back pointers (to associativity entities)

text pointers (to general note entities)

9 DE Pointer .

. Pointers to associativities or general notes

. .

n DE Pointer

n m Integer Number of properties

n DE Pointer

. Pointers to properties

. .

m DE Pointer .

Figure C.6. Parameter data for circular arc entity #100.

In other words the entity deﬁnes a cubic planar spline that is continuous and has slope

continuity at the six breakpoints T(i) = i, i = 0, 1,..., 5.

AY BY CY DY E E

TPZ TPZ TPZ TPZ

1 1 1 1 3 0 0 1481045 01 0 2384186 06 3784813 0

0 1 2 3 0000

() () () ()()

=- +- -

()

, , , .,. ,. ,. ,,

, , , . ,. ,. ,. .

CTYPE H NDIM N T i i i

AX BX CX DX

== ==

()

() () () ()()

()

31 25 015

1 1 1 1 3 0 8722851 0000003576279 01331125

, , , , , , ,..., ,

, , , . ,. ,. , . ,

830 Appendix C IGES

Parameter Name Type Description

æææææææææææææææææææææææææææææææææ

1 CTYPE Integer Spline type

1 = linear 4 = Wilson-Fowler

2 = quadratic 5 = modiﬁed Wilson-Fowler

3 = cubic 6 = B-spline

2 H Integer Continuity with respect to arc length at breakpoints

1 = curve is continuous and has slope continuity

2 = curve is continuous and has both slope and

curvature continuity

3 NDIM Integer 2 = planar

3 = non-planar

4 N Integer Number of segments

5 T(1) Real Break points of piecewise polynomial

N T(N

1) Real

6+N AX(1) Real x-Coordinate polynomial

7+N BX(1)

N CX(1)

N DX(1)

10+N AY(1) . y-Coordinate polynomial

N DY(1)

14+N AZ(1) . z-Coordinate polynomial

N AX(2)

. .

13N TPX0 . Terminate point x-value

. TPX1 . Terminate point x-value of 1

derivative

TPX2 Terminate point x-value of 2

derivative/2!

TPX3 Terminate point x-value of 3

derivative/3!

TPY0 . Terminate point y-value

. .

Figure C.7. Parameter data for parametric spline curve entity #112.

Entity Number 106. The copious data entity has multiple meanings depending on

its form number. Figure C.8 describes some of the ﬁelds of its parameter data. When

the form number is 1, 2, or 3, then the IP ﬁeld takes on the same value and they both

have the same meaning. Its data starts in parameter data line number 70 and consists

of 3 lines altogether. In our case

and we have ﬁve data points

How the points are interpreted is usually determined by the entity that refers to this

one as we shall see when we discuss the next entity.

Entity Number 108. This is the plane entity. There is one parameter data line for

it and that line has number 73. Figure C.9 describes some, but not all, parameters

that can be associated to it. In our case we have

034 01 03401 034101 0341 01 034 01, , ., , ,., , .,., , ., ., , , ..-

()()( )

()

form number == =IP N25,,

C.3 The IGES Geometric Types 831

Parameter Name Type Description

ææææææææææææææææææææææææææææ

1 IP Integer Interpretation flag

IP = 1 x, y pairs, common z

IP = 2 x, y, z triples

IP = 3 x, y, z coordinates

i, j, k vector coordinates

2 N Integer Number of n-tuples

Case IP = 2:

3N Sequence of x, y, z tuples of data values

Figure C.8. Partial parameter data for copious entity #106.

Parameter Name Type Description

æææææææææææææææææææææææææææææææææ

1 A Real Corresponds to plane

2 B Real

3 C Real Ax + By + Cz = D

4 D Real

5 DE Pointer Pointer to directory entry of closed curve entity or 0

Figure C.9. Partial parameter data for plane entity #108.

Because DE is nonzero, we have a closed curve in our plane that happens to be the

copious data entity described above consisting of ﬁve points in the plane x = 0.

C.4 The IGES Nongeometric Types

Figure C.10 lists the nongeometric entity types for IGES version 3.0.

Entity Number 406. Property entities can contain numerical or textual data. The

form number speciﬁes the type of property at hand. Low numbers are predeﬁned and

numbers 5001–9999 are left for a user to deﬁne. In our case, the form number 5555

is a user-deﬁned property. The ﬁrst number in the parameter data section after the

entity number is the number of properties. In our case, it is 1 and the property is the

string “01”.

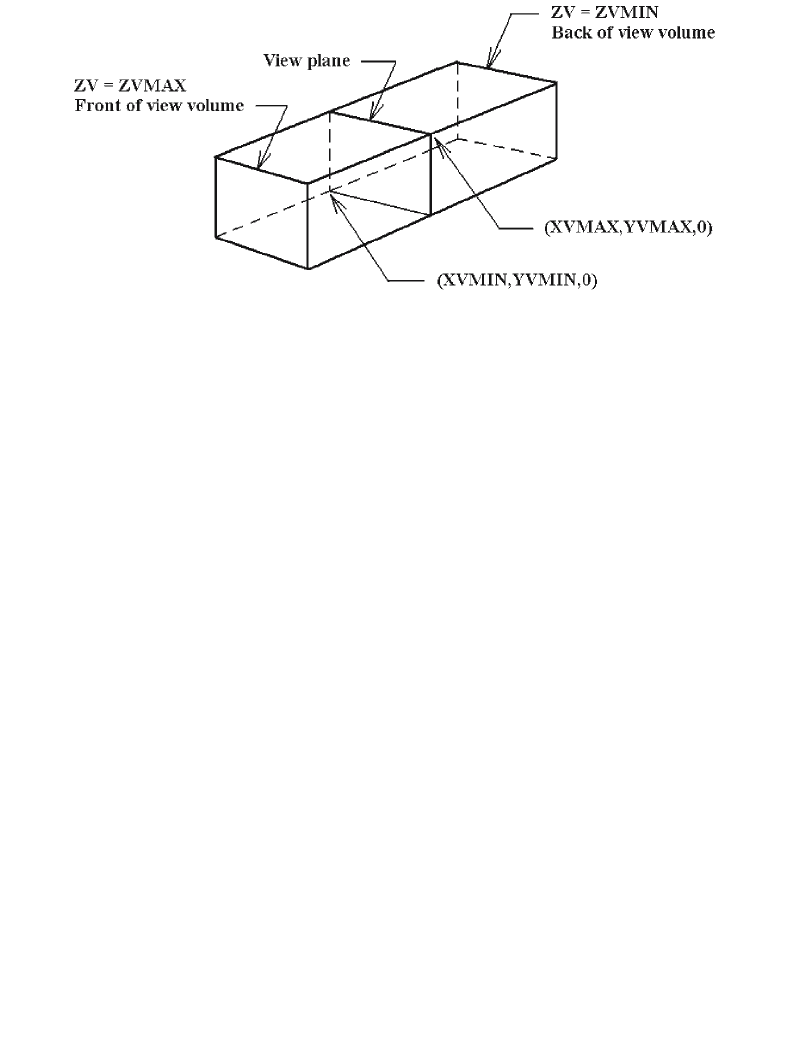
Entity Number 410. A view entity speciﬁes how an object should be viewed. The

projection is assumed to be a parallel orthographic projection. In the view coordinate

system the view plane is assumed to be the plane z = 0 with the origin being the origin

of the view plane. The view direction is along the positive z-direction. The positive y-

axis is the “up” direction. One can also specify a view volume and scale factor. Figure

C.11 shows the layout of the view volume. In the case of our entity, the fact that the

status is physically dependent and the entity use ﬂag is “other” means that a drawing

entity number 404 points to it. See Figure C.12 for a description of the ﬁelds in the

parameter data. In our case,

ABC DDE==== =1000 51,,,, .

832 Appendix C IGES

Annotation Entities Structure Entities

Entity type # Entity type Entity type # Entity type

æææææææææææææææææ æææ æææææææææææææææææ

202 Angular dimension entity 302 Associativity deﬁnition entity

106 Centerline entity 402 Associativity instance entity

206 Diameter dimension entity 404 Drawing entity

208 Flag note entity 304 Line font definition entity

210 General label entity 306 MACRO definition entity

212 General note entity 600-699 MACRO instance entity

214 Leader (arrow) entity 406 Property entity

216 Linear dimension entity 308 Subﬁgure deﬁnition entity

218 Ordinate dimension entity 408 Singular subﬁgure instance entity

220 Point dimension entity 412 Rectangular array subﬁgure

222 Radius dimension entity instance entity

106 Section entity 414 Circular array subfigure instance

106 Witness line entity entity

310 Text font definition entity

410 View entity

Figure C.10. Some IGES annotation and structure entities.

A view volume has been speciﬁed. In general, a zero would indicate no clipping in a

particular direction. We analyzed the XVMIN clipping plane corresponding to entity

VNO SCALE

XVMINP YVMAXP XVMAXP

YVMINP ZVMINP ZVMAXP

===

== =

110

53 57 61

65 69 73

,.,

,,,

,, .

C.4 The IGES Nongeometric Types 833

Figure C.11. The view volume for entity number 410.

Parameter Name Type Description

æææææææææææææææææææææææææææææææææ

1 VNO Integer View number

2 SCALE Real Scale factor (default = 1.0)

3 XVMINP Pointer Pointer to left side of view volume (XVMIN plane) or 0

4 YVMAXP Pointer Pointer to top of view volume (YVMAX plane) or 0

5 XVMAXP Pointer Pointer to right side of view volume (XVMAX plane) or 0

6 YVMINP Pointer Pointer to bottom of view volume (YVMIN plane) or 0

7 ZVMINP Pointer Pointer to back of view volume (ZVMIN plane) or 0

8 ZVMAXP Pointer Pointer to front of view volume (ZVMAX plane) or 0

Figure C.12. Partial parameter data for plane entity #410.

Parameter Name Type Description

æææææææææææææææææææææ

1 N Integer Number of entries

2 DE Pointer Pointer to entity 1

. . . .

N+1 DE Pointer Pointer to entity N

Figure C.13. Parameter data for associativity instance entity #402 with form number 1.

53 in the last section. Our view entity has no pointers to associativity instances,

general notes, or text template entities and one pointer to a property (on directory

section line number 75).

In closing, we mention one other handy entity, the associativity instance entity

with number 402. There are a number of variants of it depending on the form number.

The so-called group associativities are particularly useful because they allow a col-

lection of a set of entities to be maintained as a single, logical entity. A common one

of these is the case where the form number is 1. This requires an (unordered) group

of back pointers as the parameter data. The general structure for its data is shown in

Figure C.13.

834 Appendix C IGES

[Taub94] Taubin, Gabriel, “Rasterizing Algebraic Curves and Surfaces,” CG&A, 14(2), March 1994,

14–23.

Algebraic Geometry

[Arno83] Arnon, D.S., “Topologically Reliable Displays of Algebraic Curves,” SIGGRAPH 83, 17(3), July

1983, 219–227.

[Shaf94] Shafarevich, Igor R., Basic Algebraic Geometry I, 2

Edition, Springer-Verlag, 1994.

Algebraic Topology

(See also Topology).

[BotM58] Bott, R., and Milnor, J., “On the Parallelizability of the Spheres,” Bull. AMS, 64, 1958, 87–89.

[DelE95] Delﬁnado, Cecil Jose A., and Edelsbrunner, Herbert, “An Incremental Algorithm for Betti

Numbers of Simplicial Complexes on the 3-Sphere,” CAGD, 12(7), November 1995, 771–784.

[Matv03] Matveev, S., Algorithmic Topology and Classiﬁcation of 3-Manifolds, Springer-Verlag, 2003.

[Stee51] Steenrod, Norman, The Topology of Fiber Bundles, Princeton Univ. Press, 1951.

Analytic Geometry

[Full73] Fuller, Gordon, Analytic Geometry, 4

Edition, Addison-Wesley Publ. Co., 1973.

[Limi44] Liming, R.A., Practical Analytical Geometry with Applications to Aircraft, MacMillan, 1944.

Antialiasing

(See also Visible Surface Detection)

[AbWW85] Abram, G., Westover, L., and Whitted, T., “Efﬁcient Alias-free Rendering Using Bit-masks and

Look-up Tables,” SIGGRAPH 85, 19(3), July 1985, 53–59.

[Crow77a] Crow, Franklin C., “The Aliasing Problem in Computer-generated Shaded Images,” CACM,

20(11), 1977, 799–805.

[Will83] Williams, Lance, “Pyramidal Parametrics,” SIGGRAPH 83, 17(3), July 1983, 1–11.

Blending

[AllD97a] Allen, Seth, and Dutta, Debasish, “Cyclides in Pure Blending I,” CAGD, 14(1), January 1997,

51–75.

[AllD97b] Allen, Seth, and Dutta, Debasish, “Cyclides in Pure Blending II,” CAGD, 14(1), January 1997,

77–102.

[AllD97c] Allen, Seth, and Dutta, Debasish, “SuperCyclides and Blending,” CAGD, 14(7), September

1997, 637–651.

[BloW89a] Bloor, M.I.G., and Wilson, M.J., “Generating Blend Surfaces Using Partial Differential

Equations,” CAD, 21(3), April 1989, 165–171.

[BloW89b] Bloor, M.I.G., and Wilson, M.J., “Blend Design as a Boundary-Value Problem,” in [StrS89],

221–234.

[Chiy87] Chiyokura, H., “An Extended Rounding Operation for Modeling Solids with Free-Form

Surfaces,” in Computer Graphics, Kunii, T.L., editor, Springer, 1987, 249–268.

[ChiK83] Chiyokura, H., and Kimura, F., “Design of Solids with Free-Form Surfaces,” SIGGRAPH 83,

17(3), July 1983, 289–298.

[ChoJ89] Choi, B.K., and Ju, S.Y., “Constant Radius Blending in Surface Modeling,” CAD, 21(4), May

1989, 213–220.

[ElbC97] Elber, Gershon, and Cohen, Elaine, “Filleting and Rounding Using Trimmed Tensor Product

Surfaces,” in [HofB97], 206–216.

[HofH85] Hoffmann, Christoph M., and Hopcroft, John E., “Automatic Surface Generation in Computer

Aided Design,” The Visual Computer, 1, 1985, 95–100.

[HofH87] Hoffmann, Christoph M., and Hopcroft, John E., “The Potential Method for Blending

Surfaces and Corners,” in [Fari87], 347–365.

[HsuT98] Hsu, Kun Lung, and Tsay, Der Min, “Corner Blending of Free-form N-Sided Holes,” CG&A,

18(1), January/February 1998, 72–78.

836 Bibliography

[Prat89] Pratt, M.J., “Cyclide Blending in Solid Modelling,” in [StrS89], 235–245.

[RoaM92] Roach, P.A., and Martin, R.R., “Production of Blends and Fairings by Fourier Methods,” in

Curves and Surfaces in Computer Vision and Graphics III, Warren, J.D., editor, SPIE, 1992,

162–173.

[RocO87] Rockwood, Alyn P., and Owen, John C., “Blending Surfaces in Solid Modeling,” in [Fari87],

367–384.

[RosR84] Rossignac, A.R., and Requicha, A.A.G., “Constant Radius Blending in Solid Modeling,”

Computers in Mechanical Engineering, July 1984, 65–73.

[Shen98] Shene, Ching-Kuang, “Blending Two Cones with Dupin Cyclides,” CAGD, 15(7), July 1998,

643–673.

[Shen00] Shene, Ching-Kuang, “Do Blending and Offsetting Commute for Dupin Cyclides?” CAGD,

17(9), October 2000, 891–910.

[Szil91] Szilvasi-Nagy, M., “Flexible Rounding Operation for Polyhedra,” CAD, 23(9), November 1991,

629–633.

[VaMV89] Várady, T., Martin, R.R., and Vida, J., “Topological Considerations in Blending Boundary

Representation Solid Models,” in [StrS89], 205–220.

[VaVM89] Várady, T., Vida, J., and Martin, R.R., “Parametric Blending in a Boundary Representation

Solid Modeller,” in [Hand89], 171–197.

[ViMV94] Vida, Janos, Martin, Ralph R., Várady, Tamas, “A Survey of Blending Methods that Use

Parametric Surfaces,” CAD, 26(5), May 1994, 341–365.

[Wood87] Woodwark, J.R., “Blends in Geometric Modelling,” in [Mart87], 255–298.

Clipping

[CyrB78] Cyrus, M., and Beck, J., “Generalized Two- and Three-Dimensional Clipping,” Computers and

Graphics, 3(1), 1978, 23–28.

[GreH98] Greiner, GÜnther, and Hormann, Kai, “Efﬁcient Clipping of Arbitrary Polygons,” ACM TOG,

17(2), 1998, 71–83.

[LiaB83] Liang, You-Dong, and Barsky, Brian A., “An Analysis and Algorithm for Polygon Clipping,”

CACM, 26(11), Nov., 1983, 868–877, and Corrigendum, CACM, 27(2), February 1984, 151.

[LiaB84] Liang, You-Dong, and Barsky, Brian A., “A New Concept and Method for Line Clipping,” ACM

TOG, 3(1), January 1984, 1–22.

[Mail92] Maillot, Patrick-Gilles, “A New, Fast Method for 2D Polygon Clipping: Analysis and Software

Implementation,” ACM Trans. on Graphics, 11(3), July 1992, 276–290.

[NiLN87] Nicholl, Tina M., Lee, D.T., and Nicholl, Robin A., “An Efﬁcient New Algorithm For 2-D Line

Clipping: Its Development and Analysis,” SIGGRAPH 87, 21(4), July 1987, 253–262.

[SutH74] Sutherland, I.E., and Hodgman, G.W., “Reentrant Polygon Clipping,” CACM, 17(1), January

1974, 32–42.

[Vatt92] Vatti, Bala R., “A Generic Solution to Polygon Clipping,” CACM, 35(7), July 1992, 56–63.

[Weil80] Weiler, K., “Polygon Comparison Using a Graph Representation,” SIGGRAPH 80, 14(3), July

1980, 10–18.

Color

[AgoG87] Agoston, G.A., Color Theory and its Application in Art and Design, 2

Edition, Springer-Verlag,

1987.

[Blin93] Blinn, James F., “NTSC: Nice Technology, Super Color,” CG&A, 13(2), March 1993, 17–23.

[Fish90a] Fishkin, Ken, “A Fast HSL-To-RGB Transform,” in [Glas90], 448–449.

[GerP90] Gervautz, Michael, and Purgathofer, Werner, “A Simple Method for Color Quantization:

Octree Quantization,” in [Glas90], 287–293.

[Hall89] Hall, Roy, Illumination and Color in Computer Generated Imagery, Springer-Verlag, 1989.

[Heck82] Heckbert, P.S., “Color Image Quantization for Frame Buffer Display,” SIGGRAPH 82, 16(3),

July 1982, 297–307.

[Paet90] Paeth, Alan W., “Mapping RGB Triples Onto Four Bits,” in [Glas90], 233–245.

[WuXi92] Wu, Xialin, “Color Quantization by Dynamic Programming and Principal Analysis,” ACM

TOG, 11(4), Oct., 1992, 348–372.

Bibliography 837

Computational Geometry

[Aure91] Aurenhammer, Franz, “Voronoi Diagrams—A Survey of a Fundamental Geometric Data

Structure,” ACM Computing Surveys, 23(3), September 1991, 345–405.

[BKOS97] de Berg, Mark, van Kreveld, Marc, Overmars, Mark, and Schwarzkopf, Otfried, Computational

Geometry: Algorithms and Applications, Springer-Verlag, 1997.

[BeMR94] Bern, Marshall, Mitchell, Scott, and Ruppert, Jim, “Linear-Size Nonobtuse Triangulation of

Polygons,” in Proc. of the 10

Annual Symp. on Computational Geometry, Stony Brook, New

York, June 6–8, 1994, 221–230.

[BDST92] Boissonnat, J.-D., Devillers, O., Schott, R., Teillaud, M., and Yvinec, M., “Applications of

Random Sampling to On-line Algorithms in Computational Geometry,” Discrete Comp.

Geom., 8, 1992, 51–71.

[BoiT93] Boissonnat, J.-D., and Teillaud, M., “On the Randomized Construction of the Delaunay Tree,”

Theoret. Comp. Sci., 112, 1993, 339–354.

[Chaz91] Chazelle, B., “Triangulating a Simple Polygon in Linear Time,” Discrete Comput. Geom., 6,

1991, 485–524.

[CiMS98] Cignoni, P., Montani, C., and Scopigno, R., “DeWall: A Fast Divide and Conquer Delaunay

Triangulation Algorithm in E

,” CAD, 30(5), April 1998, 333–341.

[ClaS89] Clarkson, K.L., and Shor, P.W., “Applications of Random Sampling in Computational Geom-

etry,” Discrete Comp. Geometry, 4, 1989, 387–421.

[Devi98] Devillers, Olivier, “Improved Incremental Randomized Delaunay Triangulation,” in Proc. of

the 14

Annual Symp. on Computational Geometry, Minneapolis, Minnesota, June 7–10, 1998,

ACM Press, 106–115.

[Dwye87] Dwyer, Rex A., “A Faster Divide-and-Conquer Algorithm for Constructing Delaunay Triangu-

lations,” Algorithmica, 2(2), 1987, 137–151.

[Edel87] Edelsbrunner, Herbert, Algorithms in Combinatorial Geometry, Springer-Verlag, New York,

1987.

[EtzR99] Etzion, Michal, and Rappoport, Ari, “Computing the Voronoi Diagram of a 3-D Polyhedron

by Separate Computation of its Symbolic and Geometric Parts,” in [BroA99], 167–178.

[FanP93] Fang, Tsung-Pao, and Piegl, Les A., “Delaunay Triangulation Using a Uniform Grid,” CG&A,

13(3), May 1993, 36–47.

[FanP95] Fang, Tsung-Pao, and Piegl, Les A., “Delaunay Triangulation in Three Dimensions,” CG&A,

15(5), September 1995, 62–69.

[Fort87] Fortune, Stephen J., “A Sweepline Algorithm for Voronoi Diagrams,” Algorithmica, 2(2), 1987,

153–174.

[GJPT78] Garey, M.R., Johnson, D.S., Preparata, F.P., and Tarjan, R.E., “Triangulating a Simple

Polygon,” Inform. Process. Lett., 7, 1978, 175–179.

[GreS77] Green, P.J., and Sibson, R., “Computing Dirichlet Tessellations in the Plane,” Computer

Journal, 21(2), 1977, 168–173.

[GuiS85] Guibas, Leonidas J., and Stolﬁ, Jorge, “Primitives for the Manipulation of General Subdivi-

sions and the Computation of Voronoi Diagrams,” ACM Trans. on Graphics, 4(2), April 1985,

74–123.

[LBDW92] Lavender, David, Bowyer, Adrian, Davenport, James, Wallis, Andrew, and Woodwark, John,

“Voronoi Diagrams of Set-Theoretic Solid Models,” CG&A, 12(5), September 1992, 69–77.

[LeeP77] Lee, D.T., and Preparata, F.P., “Location of a Point in a Planar Subdivision and its Applica-

tion,” SIAM J. Comp., 6. 1977, 594–606.

[LinM96] Lin, Ming C., and Manocha, Dinesh, editors, Applied Computational Geometry: Towards

Geometric Engineering, Springer Verlag, 1996.

[Lisc94] Lischinski, Dani, “Incremental Delaunay Triangulation,” in [Heck94], 47–59.

[Mulm94] Mulmuley, Ketan, Computational Geometry: An Introduction Through Randomized Algorithms,

Prentice-Hall, Inc., 1994.

[NarM95] Narkhede, Atul, and Manocha, Dinesh, “Fast Polygon Triangulation Based on Seidel’s

Algorithm,” in [Paet95], 394–397.

[Orou94] O’Rourke, Joseph, Computational Geometry in C, Cambridge Univ. Press, 1994.

[PreS85] Preparata, Franco P., and Shamos, Michael I., Computational Geometry: An Introduction,

Springer-Verlag, 1985.

[Shew96] Shewchuk, Jonathan Richard, “Triangle: Engineering a 2D Quality Mesh Generator and

Delaunay Triangulator,” in [LinM96], 203–222.

838 Bibliography