Agoston M.K. Computer Graphics and Geometric Modelling: Mathematics
Подождите немного. Документ загружается.

by
7.2.2.3. Lemma. j
*q
is a well-defined homomorphism.
Proof. First of all, by Lemma 7.2.2.2(1), the definition makes sense, since j
q
(z) Œ
Z
q
(L). To show that j
*q
is well defined, let a ΠH
q
(K) and assume that a = [z] = [z¢], z,
z¢ŒZ
q
(K). Then z - z¢ belongs to B
q
(K). Therefore,
by Lemma 7.2.2.2(2), that is, [j
q
(z)] = [j
q
(z¢)]. This proves that j
*q
is well defined.
Next, let [z
i
] = z
i
+ B
q
(K) be elements of H
q
(K). Then
Thus, j
*q
is a homomorphism and Lemma 7.2.2.3 is proved.
Definition. The maps j
*q
are called the homomorphisms on homology induced by the
chain map j. In particular, if f : K Æ L is a simplicial map, we shall let
denote the map on the homology group induced by the chain map f
#
.
Consider the simplicial complex K =∂ ·v
0
v
1
v
2
Ò. The next two examples compute
f
*q
for two simplicial maps f:K Æ K.
7.2.2.4. Example. To compute f
*q
when f is the constant map defined by f(v
i
) = v
0
.
Solution. The given f induces the constant map ΩfΩ:ΩKΩÆΩKΩ, ΩfΩ(x) = v
0
. We know
from Example 7.2.1.5 that
and
so that we only have to worry about what happens in dimensions 0 and 1. The map
f
#1
:C
1
(K) Æ C
1
(K) is obviously the zero map by definition, and so f
*1
:H
1
(K) Æ H
1
(K)
H K for q
q
()
=>01,
HK HK
01
()
ª
()
ª Z
fHKHL
qq q*
()
Æ
()
:
jj
j
jj
jj
jj
**
**
[]
+
[]
()
=+
()
+
()()
=+
()
+
()
=
()
+
()()
+
()
=
()
+
()()
+
()
+
()()
=
[]
()
+
qqq
qq
qq q
qq q q
qq
zz zzBK
zz L
zzBL
zBL zBL
zz
12 12
12
12
12
12
B
[[]
()
.
jj j
qq q q
zz zzBL
()
-
()
=-
()
Œ
()
¢¢
jj
*
[]
()
=
()
[]
Œ
()
qq q
zzzZK,.
7.2 Homology Theory 379
is also the zero map. Next, note that the group H
0
(K) is generated by the element
v
0
+ B
0
(K) and
This implies that f
*0
is the identity map.
7.2.2.5. Example. To compute f
*q
when f is defined by f(v
0
) = v
0
, f(v
1
) = v
2
, and f(v
2
)
= v
1
.
Solution. It follows from an argument similar to the one in the previous example
that f
*q
= 0 if q > 1 and f
*0
is the identity map. Only f
*1
is different this time. Recall
from Example 7.2.1.5 that
is a generator of H
1
(K). Since
it follows that f
*1
is the negative of the identity map.
The next lemma lists some basic properties of the maps f
#q
and f
*q
that are easy
to prove.
7.2.2.6. Lemma. Let f:K Æ L and g:L Æ M be simplicial maps between simplicial
complexes. Then
(1) (g
°
f)
#q
= g
#q
°
f
#q
:C
q
(K) Æ C
q
(M).
(2) (g
°
f)
*q
= g
*q
°
f
*q
:H
q
(K) Æ H
q
(M).
(3) If K = L and f = 1
K
, then f
#q
and f
*q
are also the identity homomorphisms.
Proof. This is Exercise 7.2.2.1.
Now simplicial complexes and maps are basically only tools for studying topo-
logical spaces and continuous maps. We shall show next how continuous maps induce
homomorphisms on homology groups.
Definition. Let K and L be simplicial complexes and suppose that f:ΩKΩÆΩLΩ is a
continuous map. A simplicial approximation to f is a simplicial map j:K Æ L with the
following property: If x ŒΩKΩ and if f(x) Œ s for some simplex s Œ L, then ΩjΩ(x) Œ s.
The next lemma summarizes two important properties of simplicial
approximations.
fa f BK
ff ff ff BK
BK
a
*
()
=
[]
+
[]
+
[]
()
+
()
=
()()
[]
+
()()
[]
+
()()
[]
()
+
()
=
[]
+
[]
+
[]
()
+
()
=-
1 1 01 12 20 1
01 12 20 1
02 21 10 1
#
vv vv vv
vv vv vv
vv vv vv
aBK=
[]
+
[]
+
[]
()
+
()
vv vv vv
01 12 20 1
fBKf BK BK
*
+
()()
=
()
+
()
=+
()
00 0 00 0 0 0
vvv
#
.
380 7 Algebraic Topology

7.2.2.7. Lemma. Let f : ΩKΩÆΩLΩ be a continuous map and suppose that j:K Æ L
is a simplicial approximation to f.
(1) The map ΩjΩ:ΩKΩÆΩLΩ is homotopic to f.
(2) If f = ΩyΩ, where y:K Æ L is a simplicial map, then y=j.
Proof. To prove (1), define a homotopy h:ΩKΩ¥[0,1] ÆΩLΩ between f and ΩjΩ
by
for x ŒΩKΩ and t Œ [0,1]. That h(x,t) actually lies in ΩLΩ follows from the fact that
ΩjΩ(x) and f(x) lie in a simplex of L, which means that the segment [ΩjΩ(x),f(x)] is
contained in ΩLΩ because simplices are convex.
To prove (2), let v be a vertex of K. Then w = f(v) is a vertex of L. Since a vertex
is also a 0-simplex, the definition of a simplicial approximation implies that j(v) = w.
This proves the lemma.
Part (2) of Lemma 7.2.2.7 means that the only simplicial approximation to a sim-
plicial map is the map itself. An arbitrary continuous map does not have a unique
simplicial approximation, however.
If K is a simplicial complex, define a new simplicial complex, denoted by sd(K),
as follows:
(1) The vertices of sd(K) are the barycenters b(s) of the simplices s in K.
(2) The q-simplices of sd(K), q > 0, are all the q-simplices of the form b(s
0
)b(s
1
)
···b(s
q
), where the s
i
are distinct simplices of K and s
0
Ɱ s
1
Ɱ ...Ɱ s
q
.
It is easy to show that sd(K) is a simplicial complex (Exercise 7.2.2.3) that is a sub-
division of K. Clearly, Ωsd(K)Ω=ΩKΩ.
Definition. The simplicial complex sd(K) is called the (first) barycentric subdivision
of K. The nth barycentric subdivision of K, denoted by sd
n
(K), is defined inductively
by
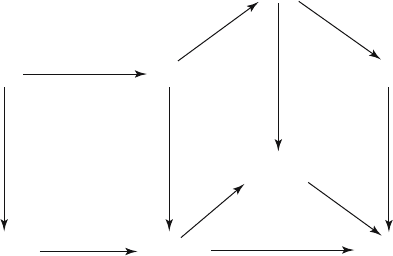
Figure 7.7 shows a simplex and its barycentric subdivision.
7.2.2.8. Theorem. (The Simplicial Approximation Theorem) Let K and L be sim-
plicial complexes and suppose that f :ΩKΩÆΩLΩ is a continuous map. Then there is
an integer N ≥ 0 such that for each n ≥ N, f admits a simplicial approximation j:
sd
n
(K) Æ L.
Proof. See [AgoM76].
sd K K
sd K sd sd K for n
nn
0
1
1
()
=
()
=
()
()
≥
-
,
,.
htt tfxx x,
()
=
()
+-
()()
j 1
7.2 Homology Theory 381

Associated to barycentric subdivisions are natural homomorphisms
that correspond to sending an oriented simplex [s] to the sum of the oriented sim-
plices into which the barycentric subdivision divides s. For example,
See Figure 7.7. More precisely, define the maps sd
#q
inductively on the oriented
simplices as follows:
(1) If v is a vertex of K, then sd
#0
(v) = v.
(2) Assume 0 < q < dim K and sd
#q-1
has been defined. If [s] is an oriented q-
simplex of K, then
(We are using the expression w[v
0
v
1
...v
q
] to denote the oriented simplex
[wv
0
v
1
...v
q
] and let this operation distribute over sums.)
If q < 0 or dim K < q, then we define sd
#q
to be the zero map.
7.2.2.9. Lemma. The maps sd
#q
are well-defined homomorphisms. Furthermore,
∂
q
°
sd
#q
= sd
#q-1
°
∂
q
, so that sd
#
= (..., sd
#-1
,sd
#0
,sd
#1
, . . .) is a chain map that induces
homomorphisms
Proof. This is an easy exercise. See [AgoM76].
We can extend our definitions and define homomorphisms
sd C K C sd K
q
n
qq
n
#
:
()
Æ
()
()
sd H K H sd K
qq q
*
:.
()
Æ
()()
sd b sd
qqq##
.ss s
[]
()
=
()
[]
()()
-1
∂
sd b b b b b b
bb b b
#2 012 012 0 01 012 01 1 012 1 12
012 12 2 012 2 02
vvv vvv v vv vvv vv v vvv v vv
vvv vv v vvv v vv
[]
()
=
()()
[]
+
()()
[]
+
()()
[]
+
()()
[]
+
()()
[]]
+
()()
[]
bbvvv vv v
012 0 2 0
.
sd C K C sd K
qq q#
:
()
Æ
()()
382 7 Algebraic Topology
v
2
b(v
0
v
2
)
b(v
0
v
1
)
b(v
1
v
2
)
b(v
0
v
1
v
2
)
v
0
v
1
K
v
2
v
1
sd (K)
v
0
Figure 7.7. A barycentric subdivision.

inductively by
The maps sd
n
#q
induce homomorphisms (actually isomorphisms)
We are now ready to show how continuous maps induce homomorphisms on
homology groups. Let K and L be simplicial complexes and let
be a continuous map. The Simplicial Approximation Theorem implies that there is an
n ≥ 0, such that f admits a simplicial approximation
Definition. The homomorphism
defined by
is called the homomorphism induced on the qth homology group by the continuous
map f.
7.2.2.10. Lemma.
(1) f
*q
is a well-defined homomorphism.
(2) If K = L and f = 1
K
, then f
*q
is the identity homomorphism.
(3) If M is a simplicial complex and g : ΩLΩÆΩMΩ is a continuous map, then
(g
°
f)
*q
= g
*q
°
f
*q
.
Proof. See [AgoM76].
7.2.2.11. Theorem. Let K and L be simplicial complexes and suppose that f,
g:ΩKΩÆΩLΩ are continuous maps that are homotopic. Then f
*q
= g
*q
:H
q
(K) Æ H
q
(L)
for all q.
Proof. See [AgoM76].
fsd
qqq
n
***
=j o
fHKHL
qq q*
()
Æ
()
:
j :.sd K L
n
()
Æ
fK L: Æ
sd H K H sd K
q
n
qq
n
*
:.
()
Æ
()
()
sd zero map for n
sd identity map of C K
sd sd sd for n
q
n
q
q
n
q
q
n
#
#
#
#
#
,,
,
,.
=<
=
()
=>
-
0
0
0
0
1
o
7.2 Homology Theory 383
7.2.3 Applications of Homology Theory
Before describing some applications, it is worthwhile to briefly pause and summarize
what we have accomplished so far; otherwise, it is easy to lose sight of the global
picture and get lost in a sequence of lemmas and theorems. The main results can be
summarized by the following:
Fact 1. For every simplicial complex K and every integer q there is an abelian group
H
q
(K) called the qth homology group of K.
Fact 2. For every continuous map f :ΩKΩÆΩLΩbetween the underlying spaces of two
simplicial complexes K and L there are a homomorphisms
whose natural properties are best summarized by the commutative diagram
fHKHL
qq q*
()
Æ
()
:
384 7 Algebraic Topology
|K|
|K|
|K|
|L|
|M|
1
H
q
(K) H
q
(K)
H
q
(L)
H
q
(M)
f
*q
(1
|K|
)
*q
g
*q
(f ¢)
*q
(g
°
f)
*q
1
H
q
(K)
f , f ¢
f f ¢
g
=
=
The top line in the diagram deals with simplicial complexes and maps and
the bottom lines deal with groups and homomorphisms.
For our purposes, Facts 1 and 2 contain essentially everything that we need to know
about homology groups and induced maps. Many of our applications will follow in a
purely formal way from Facts 1 and 2 with the geometry being irrelevant. Actual defini-
tions are only needed for a few specific computations. There is one caveat though. We
would really like to have well-defined homology groups and induced maps associated to
polyhedra and their continuous maps. Singular homology theory (see Section 7.6)
accomplishes that, but we shall at times pretend that we have this here also. To avoid
such pretense and restore rigor we could pick a fixed triangulation for each polyhedron
and translate continuous maps between them to maps between the underlying spaces of
the simplicial complexes. This would validate our arguments but the messy details
would obscure geometric ideas. By the way, homology theory can be described axiomat-
ically by means of the so-called Eilenberg-Steenrod axioms. Facts 1 and 2 correspond to
a subset of these axioms. Statements made in Chapter 6 about algebraic topology asso-
ciating “algebraic invariants” to spaces should make a lot more sense now.
7.2.3.1. Theorem. Two simplicial complexes K and L with homotopy equivalent
underlying spaces have isomorphic homology groups.
Proof. Let f :ΩKΩÆΩLΩand g : ΩLΩÆΩKΩ be continuous maps such that g
°
f 1
ΩKΩ
and f
°
g 1
ΩLΩ
. Then Fact 2 implies that
for all q. It follows that f
*q
is an isomorphism and the theorem is proved.
7.2.3.2. Corollary. Homotopy equivalent polyhedra have isomorphic homology
groups.
7.2.3.3. Corollary. If a polyhedron X has the homotopy type of a point, then
In particular, these are the homology groups of D
n
.
There is one consequence of Theorem 7.2.3.1 that would be disappointing to
anyone who might have hoped to use homology groups to classify topological spaces.
They are not strong enough invariants to distinguish spaces up to homeomorphism.
For example, Corollary 7.2.3.3 shows that both a single point and the disk D
n
have
the same homology groups but are clearly not homeomorphic. The best we could hope
for now is that they distinguish spaces up to homotopy type. Unfortunately, they fail
to do even that except in special cases. (There exist polyhedra, such as the spaces in
Example 7.2.4.7, that have isomorphic homology groups but that are not homotopy
equivalent.) Nevertheless, homology groups are strong enough to enable one to prove
many negative results, that is, if one can show that two spaces have nonisomorphic
homology groups, then it follows that the are not homeomorphic. In fact, they would
not even have the same homotopy type.
Before we state several invariance results that can be proved using homology
groups, we need to compute the homology groups for the higher-dimensional spheres.
7.2.3.4. Theorem. If n ≥ 1, then
Proof. The case n = 1 is left as an easy exercise for the reader. Assume that n ≥ 2.
Let s = v
0
v
1
···v
n
be any n-simplex. Let M =·sÒ and N =∂M be the simplicial
complexes associated to the simplex and its boundary. Since S
n-1
is homeomorphic
to ∂s =ΩNΩ, it suffices to compute H
k
(N). The definition of the simplicial homology
groups implies that
Therefore,
B N B M for k n or k n
Z N Z M for all k
kk
kk
()
=
()
££- ≥
()
=
()
,,
,.
02
H
if n and k
if n and either k or k n
if k or n
k
S
n-1
()
ª
≈= =
≥==-
π-
Ï
Ì
Ô
Ó
Ô
¸
˝
Ô
˛
Ô
ZZ
Z
,
,
,.
10
201
001
H
q
X
Z
()
ª
Ï
Ì
Ó
¸
˝
˛
,
.
q=0
0, q > 0
g f l and f g l
q q HK q q HL
qq
**
(
)
**
(
)
==oo
7.2 Homology Theory 385
and Corollary 7.2.3.3 proves Theorem 7.2.3.4 for these values of k.
To compute H
n-1
(N), note that
and so
We shall show that S is in fact a generator of Z
n-1
(N). If
then
Let s < t. The coefficient of the oriented (n - 2)-simplex [v
0
v
1
...vˆ
s
...vˆ
t
...v
n
] is
Since this coefficient has to vanish, it is easy to check that z = a
0
S. It follows that
Z
n-1
(N) = ZS. But B
n-1
(N) = 0 and Z
n-1
(N) has no elements of finite order, so that
and the theorem is proved.
7.2.3.5. Theorem.
(1) The spheres S
n
and S
m
have the same homotopy type only when n = m. In
particular, S
n
is homeomorphic to S
m
if and only if n = m.
(2) The Euclidean space R
n
is homeomorphic to R
m
only when n = m.
Proof. Part (1) follows from Theorem 7.2.3.4 and Corollary 7.2.3.2. To prove part
(2), we use the stereographic projection
p
n
n
n
n
:.Se R-Æ
+1
HNZN
nn--
()
=
()
ª
11
Z,
-
()
+-
()
-
11
1s
t
t
s
aa.
0
11
1101
0
01
1
01
10
1
=
()
= ◊◊◊ ◊◊◊
[]
()
=-
()
◊◊◊ ◊◊◊ ◊◊◊
[]
+-
()
◊◊◊ ◊◊◊ ◊◊◊
[]
Ê
--
=
-
=+=
-
Â
ÂÂ
∂∂
nin in
i
n
i
j
jin
j
ijn
ji
n
j
i
za
a
vv v v
vvvvv vvvvv
ˆ
ˆˆ ˆˆ
ËË
Á
ˆ
¯
˜
=
Â
i
n
0
.
za ZN
iinn
i
n
= ◊◊◊ ◊◊◊
[]
Œ
()
-
=
Â
vv v v
01 1
0
ˆ
,
S= ◊◊◊
[]
()
Œ
()
-
∂
nnn
ZNvv v
01 1
.
∂∂
nn n-
()
◊◊◊
[]
()
=
101
0o vv v ,
H N H M for k n
kk
()
=
()
π-,,1
386 7 Algebraic Topology

Suppose that h:R
n
Æ R
m
is a homeomorphism. Define
by
The map H will be a homeomorphism and therefore n = m by part (1). The theorem
is proved.
The next three theorems are less trivial.
7.2.3.6. Theorem. (Invariance of Dimension) If K and L are simplicial complexes
with ΩKΩªΩLΩ, then dim K = dim L.
Proof. See [AgoM76].
Definition. The dimension of a polyhedron is defined to be the dimension of any
simplicial complex that triangulates it.
Theorem 7.2.3.6 shows the dimension of a polyhedron is a well-defined topologi-
cal invariant.
7.2.3.7. Theorem. (Invariance of Boundary) If K and L are simplicial complexes
and h:ΩKΩÆΩLΩ is a homeomorphism, then h(Ω∂KΩ) =Ω∂LΩ.
Proof. See [AgoM76].
Theorem 7.2.3.7 makes it possible to define the boundary of a polyhedron.
Definition. Let X be a polyhedron. Define the boundary of X, denoted by ∂X, by
where (K,j) is any triangulation of X.
7.2.3.8. Theorem (Invariance of Domain) If U and V are homeomorphic subsets of
R
n
and if U is open in R
n
, then so is V.
Proof. See [AgoM76].
Returning to our definition of topological manifolds in Section 5.3, we are finally
able to prove the claimed invariance of two aspects of the definition.
7.2.3.9. Corollary. The dimension of a topological manifold and its boundary are
well defined.
∂j∂X =
()
K,
H p h p if and
H
mn n
nm
xxxe
ee
()
=
()
()
π
()
=
-
+
++
1
1
11
oo ,,
.
H
nm
: SSÆ
7.2 Homology Theory 387
Proof. The corollary is an easy consequence of Theorems 7.2.3.5 and 7.2.3.8.
Next, we return to the Euler characteristic as defined in Chapter 6. We are now
in a position to put this invariant in a more general context. What we had in Chapter
6 was a combinatorial concept defined for surfaces that was easy to compute by some
simple counting and yet was claimed to be a topological invariant. We can now define
that topological invariant in a rigorous manner.
Definition. If K is a simplicial complex, let n
q
(K) denote the number of q-simplices
in K and define the Euler-Poincaré characteristic of K, c(K), by
What makes c(K) a topological invariant is the fact that it is related to the Betti
numbers b
q
(K) of K.
7.2.3.10. Theorem. (The Euler-Poincaré Formula) Let K be a simplicial complex.
Then
Proof. By definition, the boundary map ∂
q
:C
q
(K) Æ B
q-1
(K) is onto and has kernel
Z
q
(K) and the natural projection Z
q
(K) Æ H
q
(K) is onto and has kernel B
q
(K). There-
fore, Theorem B.5.8 implies that
These identities and the fact that rank (C
q
(K)) = n
q
(K) gives us that
c KnK
rank C K
rank B K rank H K rank B K
rank H K rank B K
q
q
q
K
q
q
q
K
q
qqq
q
K
q
q
q
K
q
q
()
=-
() ()
=-
() ()()
=-
() ()()
+
()()
+
()()
[]
=-
() ()()
+-
() (
=
=
-
=
=
-
Â
Â
Â
Â
1
1
1
11
0
0
1
0
0
1
dim
dim
dim
dim
))()
+
()()
[]
=-
() ()()
=
=
Â
Â
rank B K
rank H K
q
q
K
q
q
q
K
0
0
1
dim
dim
rank C K rank B K rank Z K and
rank Z K rank H K rank B K
qq q
qqq
()()
=
()()
+
()()
()()
=
()()
+
()()
-1
.
cbKK
q
q
q
K
()
=-
() ()
=
Â
1
0
dim
.
c KnK
q
q
q
K
()
=-
() ()
=
Â
1
0
dim
.
388 7 Algebraic Topology
