Agoston M.K. Computer Graphics and Geometric Modelling: Mathematics

Подождите немного. Документ загружается.

(8.17)

We see that this matches equation (8.13) and the two deﬁnitions of tangent vectors

really amount to the same thing. In fact, the correspondence

(8.18)

deﬁnes the natural isomorphism between the two vector spaces that are called the

tangent space to the manifold.

Deﬁnition. Let M

and W

be differentiable manifolds and let f:M

Æ W

be a dif-

ferentiable map. If p Œ M

, then deﬁne a map

(8.19a)

(8.19b)

for every X Œ T

) and g Œ F(f(p)). The map Df(p) is called the derivative of f at p.

Just like with the previous equivalence class of vectors deﬁnition, one can show

that Df(p) is a well-deﬁned linear transformation.

No matter which deﬁnition of tangent vectors one uses, given a map f between

differentiable manifolds, the rank of f at a point p is the rank of its derivative Df(p).

Let us summarize the main points that we covered in this section. We deﬁned

abstract manifolds, tangent vectors, when a map is differentiable, and the derivative

of a map. One can show that for submanifolds of Euclidean space the notions of

tangent vectors, the derivative of a map, and the rank of a map are compatible with

those given in Section 8.4.

8.9 Vector Bundles

Bundles over a space were introduced in Section 7.4.2. The basic concept consisted

of three pieces, a total space, a projection map onto a base space, and a local trivial-

ity condition (each point of the base space had a neighborhood over which the bundle

looked like a product of the base neighborhood and another space called the ﬁber).

In Section 7.4.2 we concentrated on a very special case, that of covering spaces, where

the ﬁber was a discrete space. In this section we look at the case of where the ﬁber is

a vector space. Even though covering spaces are really part of the same general topic

of “ﬁber” bundles, for historical reasons the notation differs slightly between the two.

We shall now switch to the notation used for vector bundles. (In Section 7.4.2 we used

the expression “bundle over a space” to emphasize that the base space was not part

of the deﬁnition of “bundle”, which it will be here.)

Df X g X g fp

()( )()()

()

Df T T

pM W

()

(

)

ÂÂ

∂

aXu b

ii j

()

∂

8.9 Vector Bundles 509

Deﬁnition. An n-dimensional (real) vector bundle, or n-plane bundle, or simply vector

bundle if the dimension is unimportant, is a triple x=(E(x),p

,B(x)) = (E,p,B)

satisfying

(1) E and B are topological Hausdorff spaces.

(2) The map p:E Æ B is continuous and onto.

(3) For each b Œ B, p

-1

(b) has the structure of an n-dimensional (real) vector

space.

(4) (Local triviality) For each b Œ B, there is an open neighborhood U

of b and

a homeomorphism

such that

is a vector space isomorphism for all b¢ŒU

E is called the total space, p is called the projection, and B is called the base space for

x. The space p

-1

(b) is called the ﬁber of x over b. The pair (j

) is called a local coor-

dinate chart for the vector bundle. A one-dimensional vector bundle is often called a

line bundle. One sometimes refers to x as a vector bundle over B.

8.9.1. Example. If B is a topological space and p:B ¥ R

Æ B is the projection onto

the ﬁrst factor, then x=(B ¥ R

,p,B) is clearly an n-plane bundle called the product

n-plane bundle over B.

Example 8.9.1 shows that there are lots of vector bundles, but the theory would

not be very interesting if they all were just product bundles. We shall see examples of

other bundles shortly, but we need a few more deﬁnitions ﬁrst.

Deﬁnition. Let x=(E,p,B) be an n-plane bundle and let A Õ B. The restriction of x

to A, x|A, is the n-plane bundle x|A = (p

-1

(A),p|p

-1

(A),A).

Showing that x|A is an n-plane bundle is an easy exercise.

Deﬁnition. Let x=(E,p,B) be an n-plane bundle. A cross-section of x is a continu-

ous map

so that

that is, s(b) belongs to the ﬁber p

-1

(b) for every b Œ B. The zero cross-section is the

cross-section s where s(b) is the zero vector in p

-1

(b) for every b Œ B. A cross-section

s is said to be nonzero if s(b) is a nonzero vector in the vector space p

-1

(b) for every

p o s =1

sB E: Æ

¢¥ ¢¥ Æ ¢

()

bRbR b:

bb b

U R U: ¥Æ

()

-n1

510 8 Differential Topology

b Œ B. The support of a cross-section s, denoted by support(s), is deﬁned to be the set

of b Œ B with s(b) π 0. Two cross-sections s

and s

are said to be linearly independ-

ent if s

(b) and s

(b) are linearly independent vectors in p

-1

(b) for every b Œ B.

See Figure 8.28. It is easy to see that the set of cross-sections of a vector bundle

x is actually a vector space. In fact, if s is a cross-section of x and f is a real-valued

function on the base space B of x, then we can deﬁne a new cross-section fs for x by

means of the obvious formula

Note. Every vector bundle has the zero cross-section. One often identiﬁes the base

space of a vector bundle with the image of this zero cross-section in the total space,

namely, the space of zero vectors in all the ﬁbers.

Next, we deﬁne what is meant by a map between vector bundles. Such a map

should preserve ﬁbers and the vector space structure.

Deﬁnition. Let x

= (E

) be vector bundles (of possibly different dimensions). A

vector bundle map F:x

Æx

is a pair of maps (f

,f), so that

(1) the diagram

commutes, that is, p

= f p

, and

(2) the ﬁber maps

are linear transformations with respect to the vector space structure on each

ﬁber for all b

Œ B

˜˜

:ff f

bbb b

()

() ()

()()

-- -

pp p

æÆæ

ØØ

æÆæ

fs f s for all

()()

Œbbb bB,.

8.9 Vector Bundles 511

cross-section s

zero section

s(b)

Figure 8.28. Cross-sections.

The map F is called a vector bundle isomorphism if f is a homeomorphism and f

is a

vector space isomorphism on each ﬁber (or, equivalently, f

is a homeomorphism

between E

and E

). We say that x

and x

are isomorphic vector bundles, and write

ªx

, if there exists a vector bundle isomorphism between them. An n-plane bundle

x=(E,p,B) that is isomorphic to the product bundle (B ¥ R

, projection onto B,B) is

called a trivial vector bundle.

Clearly, if F = (f

,f) is a vector bundle isomorphism, then F

-1

= (f

-1

) is a vector

bundle isomorphism called the inverse of F. One can also compose vector bundle

maps.

Now, one way of thinking of vector bundles is as locally trivial bundles with ﬁber

a vector space, that is, if x is an n-plane bundle over a space B, then there will exist

a covering of B by open sets U, so that x|U is trivial. To put is yet another way, an n-

plane bundle over a space B consists of a collection of product bundles (U ¥ R

,pro-

jection onto U,U) for open sets U in B that are glued together along their ﬁbers using

maps in GL(n,R). We shall make this clearer later when we discuss the tangent bundle

of a manifold. The generalization of this way of looking at a vector bundle is what is

called a ﬁber bundle (also written “ﬁbre” bundle) where we allow an arbitrary space to

be the ﬁber except that one is also explicitly given a group which acts on the ﬁbers.

In our case, this group would be GL(n,R).

Returning to the topic of cross-sections, an interesting question is whether or not

a vector bundle has a nonzero cross-section. Trivial bundles (other than the 0-dimen-

sional ones) certainly have lots of nonzero cross-sections. In fact, a trivial n-plane

bundles has n linearly independent cross-sections (Exercise 8.9.1). Therefore, a vector

bundle that has no nonzero cross-section cannot be trivial and this becomes one of

the tests for triviality.

It is time to give an example of a nontrivial vector bundle.

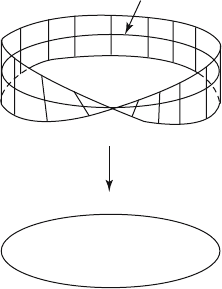
8.9.2. Example. Our nontrivial vector bundle is easy to describe in rough terms,

although it will take a little more work to explain rigorously. Basically, we are talking

about an “open” Moebius strip thought of as the total space of a line bundle (E,p,S

)

over the circle. See Figure 8.29. In a sense, we are simply removing the boundary of

512 8 Differential Topology

meridian

Figure 8.29. The open Moebius strip line bundle.

the Moebius strip deﬁned in Chapter 6, but we shall modify our earlier construction

to match the vector bundle structure better. To this end, let the total space E be the

space [0,p] ¥ R with the two ends glued together after giving one end a 180° twist,

that is, the point (0,t) is identiﬁed with the point (p,-t). The base space is the center

line, or meridian, [0,p] ¥ 0 with the end point (0,0) glued to the end point (p,0). What

we get is a circle that is identiﬁed with S

and we have the obvious projection map p

which maps each ﬁber c ¥ R to c. The space E is obviously not homeomorphic to S

¥ R and so the bundle is not trivial. This is the quick and dirty description of the line

bundle we are after, but ﬁlling in the missing details would be a little messy. There-

fore, we shall now describe a quite different construction for the “same” bundle, one

that leads to a nice generalization in Section 8.13.

Let

be the standard 2-fold covering of P

, which maps every point q Œ S

into the equiv-

alence class

Deﬁnition. The canonical line bundle g=(E,p,P

) over P

is deﬁned as follows:

(1) E = {([q],tq) Œ P

¥ R

| t Œ R}.

(2) p([q],tq) = [q].

To show that g is a vector bundle, we must show that the ﬁbers have a vector space

structure and that the bundle is locally trivial. Since the ﬁbers of this bundle are just

the lines through the origin in R

, we can obviously consider them as one-dimensional

vector spaces. To prove the locally triviality property deﬁne sets

(8.26)

The sets U

are open sets whose union is P

. Deﬁne homeomorphisms

where x = [q] and the representative q for x is chosen so that q

> 0. It is easy to check

that the maps j

are well-deﬁned homeomorphisms because the sets U

do not contain

antipodal points. This ﬁnishes the proof that g is a line bundle. Exercise 8.9.2 asks the

reader to show that g is isomorphic to the open Moebious strip bundle described

above.

Finally, we prove that the line bundle g is not trivial by showing that it does not

admit any nonzero cross-section. Suppose that g had a nonzero cross-section s. It

would follow that the map

ttxxq,,,

()

ii i

: UR U¥Æ

()

-1

.Uq SR S U UP

iiii

q q q and p==

()

ŒÃ >

{}

Ã=

()

12 1 1

qqqP

[]

{}

Œ,

p: SP

8.9 Vector Bundles 513

would have the form

(8.27)

for some continuous map

(Exercise 8.9.3). Such a map a takes on both positive and negative values. Since S

connected, the intermediate value theorem implies that a must be zero somewhere,

which contradicts the hypothesis that s was a nonzero cross-section. This ﬁnishes

Example 8.9.2.

Here are some important constructions deﬁned for vector bundles.

Deﬁnition. Let x

= (E

) be vector bundles. The vector bundle x

¥x

= (E

¥p

¥ B

) is called the vector bundle product of x

and x

It is trivial to show that x

¥x

is in fact a vector bundle.

Deﬁnition. Let j=(E,p,B) be an n-plane bundle and let f :B

Æ B be a map. Deﬁne

an n-plane bundle f*x=(E

) over B

as follows:

(1) E

= {(b

,e) Œ B

¥ E | f(b

) =p(e)}

(2) p

,e) = b

(3) The vector space structure for each ﬁber p

-1

) is deﬁned by

(4) Let b

Œ B

and let

be a local coordinate chart for x over a neighborhood U of f(b

). If V = f

-1

(U),

then the map

deﬁned by

¢,v) = (b

¢,j(f(b

¢),v)).

is a local coordinate chart for x

over V.

:,U ¥Æ

()

jp: UR U¥Æ

()

-n1

r s r s for r sbe be b e e R

111

,,,,,.

()

+¢

()

=+¢

()

aaa:.SR q q

Æ-

()

with

spo

()()

[]

()()

qqqq,,a

spo : SE

514 8 Differential Topology

The vector bundle f*x is called the induced (vector) bundle over B

, the (vector) bundle

over B

induced by f, or the pullback (vector) bundle. Deﬁne

The bundle map (f

,f):f*xÆxis called the canonical (vector bundle) map from f*j

to x.

8.9.3. Lemma. f*x is a well-deﬁned n-plane bundle and (f

,f) is a vector bundle map.

Proof. Easy.

We collect the main facts about induced bundles in the next theorem.

8.9.4. Theorem.

(1) If (f

,f):hÆxis a vector bundle map between two n-plane bundles h and x,

then the induced vector bundle f*x is isomorphic to h.

(2) If j=(E,p,B) is a trivial vector bundle over B and if f :B

Æ B is a map, then

f*j is a trivial vector bundle over B

(3) Let x=(E,p,B) be a vector bundle. If B

is a paracompact space and if f, g:

Æ B are homotopic maps, then the induced bundles f*x and g*x are iso-

morphic.

Proof. To prove (1) show that the vector bundle map

deﬁned by

is the desired isomorphism. Fact (2) is easy. For fact (3) see [Huse66].

8.9.5. Corollary. Every vector bundle over a contractible paracompact space B is

trivial.

Proof. Let f be the identity map on B and let g:B Æ B be a constant map. If x is

any vector bundle over B, then f*x is easily seen to be isomorphic to x and g*x is trivial

by Theorem 8.9.4(2). Since f is homotopic to g, the Corollary now follows from

Theorem 8.9.4(3).

Next, we show how vector bundles over a space can be added.

gfeee

()

() ()

()

,: *gf1

B h

(

)

()

,.f be e

()

:f EE

8.9 Vector Bundles 515

Deﬁnition. Let x

= (E

,B) be an n-plane bundle and x

= (E

,B) an m-plane

bundle over the same base space B. Deﬁne the Whitney sum of x

and x

, denoted by

≈x

, to be the vector bundle (E,p,B), where

(1) E = {(e

) Œ E

¥ E

) =p

)},

(2) p(e

) =p

(3) the vector space structure for each ﬁber p

-1

(b) =p

-1

(b) ¥p

-1

(b) is just the

direct sum vector space structure, and

(4) if b Œ B and if

are local coordinate charts for x

and x

, respectively, over a neighborhood U

of b, then

deﬁned by

is a local coordinate chart for x

≈x

over U.

8.9.6. Lemma. x

≈x

is a well-deﬁned (n + m)-dimensional vector bundle.

Proof. Easy.

One very useful notion for vector spaces is that of an inner product because then

one can talk about the length of vectors and whether two are orthogonal. It is con-

venient to have these concepts for vector bundles.

Deﬁnition. A Riemannian metric on a vector bundle x is a continuous function

such that the restriction of m to each ﬁber is a positive deﬁnite quadratic form.

8.9.7. Theorem. Every vector bundle over a paracompact space admits a Rie-

mannian metric.

Proof. See [Spiv70a].

Note. Because of the equivalence between quadratic forms and symmetric bilinear

maps, a Riemannian metric on a vector bundle x is sometimes deﬁned to be a con-

tinuous function

()

≈

()

Æ,:EE Rxx

mx: ER

()

jjj¢

()()

=¢

()

()()

ŒŒb v,w bv bw v R w R,,,,,,,

jp:,UR U¥Æ

()

+-nm 1

jp j p

::UR U UR U¥Æ

()

¥Æ

()

and

516 8 Differential Topology

with the property that <,> is a positive deﬁnite symmetric bilinear map (inner product)

on each ﬁber. We shall feel free to switch between these two equivalent deﬁnitions of

a Riemannian metric.

Once a vector bundle has a Riemannian metric, then the terms “length”, “orthog-

onality”, “angle”, etc., will all make sense with regard to vectors in a ﬁber. One can

also deﬁne two natural sub-bundles.

Deﬁnition. Let x=(E,p,X) be a vector bundle with Riemannian metric m. Deﬁne

The bundles D(x) = (E

,p|E

,X) and S(x) = (E

,p|E

,X) are called the disk bundle and

sphere bundle associated to x, respectively.

Clearly, the disk and sphere bundles associated to an n-dimensional vector bundle

have ﬁbers homeomorphic to D

and S

n-1

, respectively.

Finally, we deﬁne what it means for a vector bundle to be oriented.

Deﬁnition. Let x=(E,p,B) be a vector bundle. Let s be a map that associates to each

b Œ B an orientation of the vector space p

-1

(b). Such a choice is said to be a contin-

uously varying choice of orientations if for every local coordinate chart (j

) for x

and all b¢ŒU

where the vector space isomorphism

is deﬁned by

(In other words, the orientations s(b¢) are the orientations induced from s(b) using

the isomorphisms T

b¢

. See equation (8.8b).) An orientation of a vector bundle is a con-

tinuously varying choice of orientations in each ﬁber. A vector bundle is said to be

orientable if it admits an orientation. An oriented vector bundle is a pair (x,s), where

x is a vector bundle and s is an orientation of x.

8.9.8. Examples. It is easy to see that any trivial vector bundle is orientable. The

canonical line bundle g=(E,p,P

) over P

is not orientable because a line bundle is

orientable if and only if it is trivial (Exercise 8.9.4).

Other examples pertaining to the orientability of vector bundles can be found in

the next section.

Deﬁnition. Let (x

) and (x

) be two oriented n-plane bundles and let F = (f

,f):x

Æx

be a bundle map. We say that F is an orientation-preserving bundle map if

deﬁnes an orientation-preserving vector space isomorphism on each ﬁber of x

. We

()

=¢

()

vbvj ,.

()

Æ¢

()

bb: pp

ss¢

()

()()()

E eEe E eEe

=Œ

()

{}

=Œ

()

{}

mm11and .

8.9 Vector Bundles 517

say that F is an orientation-reversing bundle map if f

deﬁnes an orientation-reversing

vector space isomorphism on each ﬁber of x

The pullback of an oriented vector bundle has a natural orientation because ﬁbers

get mapped isomorphically onto ﬁbers and so we can simply pull back the orienta-

tion with the inverse of the isomorphism. More precisely,

Deﬁnition. Let (x,s) be an oriented n-plane bundle and let f:B

Æ B(x) be a map.

The induced orientation f*s on f*x is deﬁned as follows: Let (f

,f):f*xÆxbe the canon-

ical map with ﬁber maps f

. If b

Œ B

, then

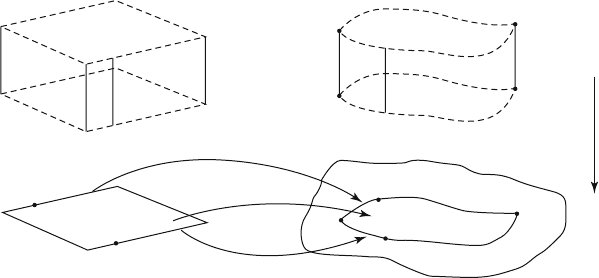
8.9.9. Theorem. Any vector bundle x=(E,p,B) over a simply connected space B is

orientable.

Proof. See Figure 8.30. Fix a point b

in B. Choose an orientation s

in p

-1

). Let

b Œ B. We shall deﬁne an orientaton s for x so that s(b

) =s

. Since B is path-

connected, there is a path g:I Æ B so that g(0) = b

and g(1) = b. By Corollary 8.9.5,

g*x is a trivial bundle over I, which means that g*x admits a unique orientation h

that h

(0) is mapped to s

by the canonical map from g*x to x. See Exercise 8.9.5 for

the uniqueness part. Let s(b) be the orientation of p

-1

(b) to which h

(1) is mapped by

the canonical map from g*x to x. We need to show that

(1) s is a well-deﬁned map, and

(2) s is a continuously varying choice of orientations in each ﬁber.

We shall only prove (1) and leave (2) as an exercise for the reader. Suppose that there

is another path l:I Æ B so that l(0) = b

and l(1) = b. Again, choose the unique ori-

entation h

for l*x so that h

(0) is mapped to s

by the canonical map from l*x to x.

We must show that h

(1) maps to s(b). Since B is simply connected, there is a

homotopy

fff

.ss

()( )

() ()()()

bb b

518 8 Differential Topology

E(h*x)

(t,0)

(t,1)

I ¥ I ¥ R

I ¥ I

0 ¥ I

I ¥ 0

I ¥ 1

1 ¥ I

(t,1) ¥ R

–1

)

–1

(l(t))

–1

(b)

l(t)

g (t)

Figure 8.30. Proving Theorem 8.9.9.