Ahsan A. (ed.) Evaporation, Condensation and Heat transfer

Подождите немного. Документ загружается.

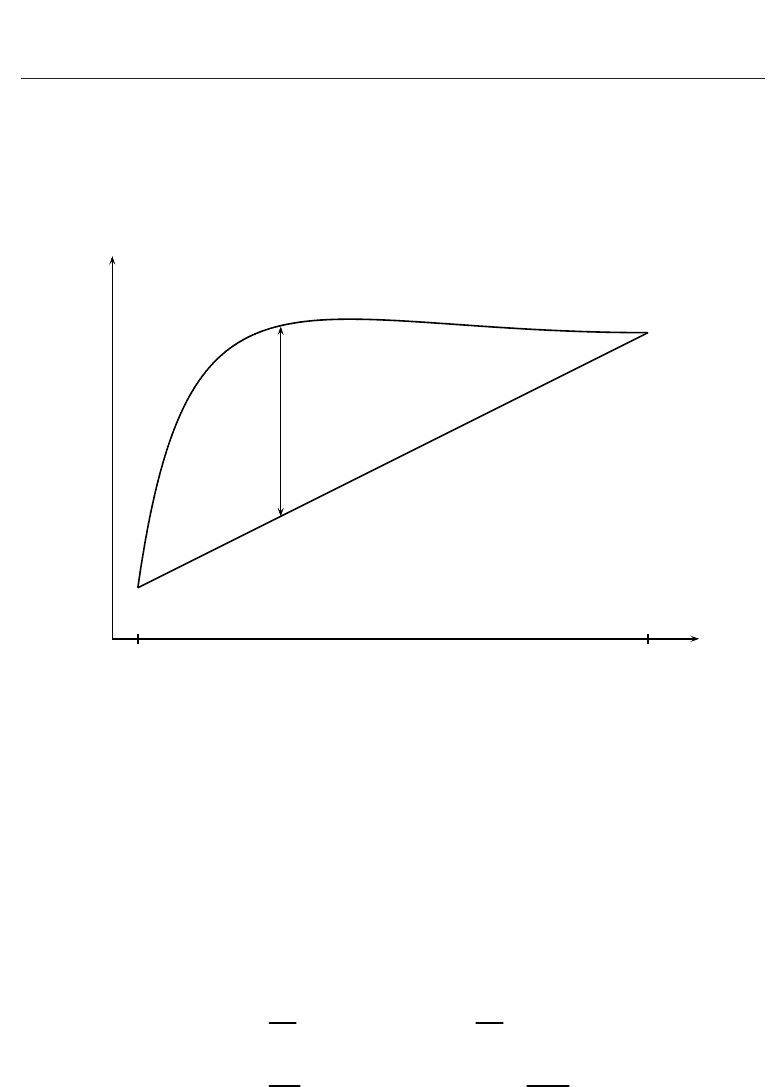
Soret and Dufour Effects on Steady MHD Natural Convection Flow Past a Semi-Inﬁnite Moving Vertical Plate in a Porous Medium with Viscous Dissipation in the Presence of

a Chemical Reaction 5

Deﬁne a function Z

(x) to represent the vertical difference between Y(x) and the initial guess

(x),thatis

(x)=Y(x) − Y

(x),orY(x)=Y

(x)+Z

(x). (17)

For example, the vertical displacement between the variable y

(x) and its corresponding

initial guess y

1,0

(x) is z

1,1

= y

(x) − y

1,0

(x). This is shown in Figure 1.

1,1

1,0

(

)

= y

(x)

Fig. 1. Geometric representation of the function z

1,1

(x)

Substituting equation (17) in (11) gives

, Z



, Z



,...,Z

(n)

]+N[Y

, Y



, Y



,...,Y

(n)

+ Z

(n)

]=−L [Y

, Y



, Y



,...,Y

(n)

(18)

Since Y

(x) is an known function, solving equation (18) would yield an exact solution for

(x). However, since the equation is non-linear, it may not be possible to ﬁnd an exact

solution. We therefore look for an approximate solution which is obtained by solving the

linear part of the equation assuming that Z

and its derivatives are small. This assumption

enables us to use the Taylor series method to linearise the equation. If Z

(x) is the solution

of the full equation (18) we let Y

(x) denote the solution of the linearised version of (18).

Expanding (18) using Taylor series (assuming Z

(x) ≈ Y

(x)) and neglecting higher order

terms gives

, Y



, Y



,...,Y

(n)



∂N

∂Y







,...,Y

(n)

)



∂N

∂Y









,...,Y

(n)

)





∂N

∂Y









,...,Y

(n)

)



+ ...+



∂N

∂Y

(n)







,...,Y

(n)

)

(n)

= −L[Y

, Y



, Y



,...,Y

(n)

] − N[ Y

, Y



, Y



,...,Y

(n)

]. (19)

329

Soret and Dufour Effects on Steady MHD Natural Convection Flow Past

a Semi-Infinite Moving Vertical Plate in a Porous Medium with Viscous Dissipation ...

6 Mass Transfer

The partial derivatives inside square brackets in equation (19) represent Jacobian matrices of

size k

× k,deﬁnedas



∂N

∂Y



⎡

⎢

⎣

∂N

∂y

1,i

∂N

∂y

2,i

···

∂N

∂y

k,i

∂N

∂y

1,i

∂N

∂y

2,i

···

∂N

∂y

k,i

∂N

∂y

1,i

∂N

∂y

2,i

···

∂N

∂y

k,i

⎤

⎥

⎦

⎡

⎣

∂N

∂Y

(p)

⎤

⎦

⎡

⎢

⎣

∂N

∂y

(p)

1,i

∂N

∂y

(p)

2,i

···

∂N

∂y

(p)

k,i

∂N

∂y

(p)

1,i

∂N

∂y

(p)

2,i

···

∂N

∂y

(p)

k,i

∂N

∂y

(p)

1,i

∂N

∂y

(p)

2,i

···

∂N

∂y

(p)

k,i

⎤

⎥

⎦

(20)

where i

= 1andp is the order of the derivatives.

Since the right hand side of equation (19) is known and the left hand side is linear, the equation

can be solved for Y

(x). Assuming that the solution of the linear part (19) is close to the

solution of the equation (18), that is Z

(x) ≈ Y

(x), the current estimate (1st order) of the

solution Y

(x) is

(x) ≈ Y

(x)+Y

(x). (21)

To improve on this solution, we deﬁne a slack function, Z

(x), which when added to Y

(x)

gives Z

(x) (see Figure 2 for example), that is

(x)=Z

(x)+Y

(x). (22)

2,1

1,1

1,0

(

)

= y

(x)

Fig. 2. Geometric representation of the functions z

2,1

Since Y

(x) is now known (as a solution of equation 19), we substitute equation (22) in

equation (18) to obtain

330

Evaporation, Condensation and Heat Transfer

Soret and Dufour Effects on Steady MHD Natural Convection Flow Past a Semi-Inﬁnite Moving Vertical Plate in a Porous Medium with Viscous Dissipation in the Presence of

a Chemical Reaction 7

L[Z

, Z



, Z



,...,Z

(n)

]+N[Y

+ Y

+ Z

+, Y



+ Y



+ Z



,...,Y

(n)

+ Y

(n)

+ Z

(n)

]

= −L[

+ Y

, Y



+ Y



, Y



+ Y



,...,Y

(n)

+ Y

(n)

]. (23)

Solving equation (23) would result in an exact solution for Z

(x). But since the equation is

non-linear, it may not be possible to ﬁnd an exact solution. We therefore linearise the equation

using Taylor series expansion and solve the resulting linear equation. We denote the solution

of the linear version of equation (23) by Y

(x),suchthatZ

(x) ≈ Y

(x). Setting Z

(x)=Y

(x)

and expanding equation (23), for small Y

(x) and its derivatives gives

, Y



,...,Y

(n)



∂N

∂Y





,...,Y

(n)

)



∂N

∂Y







,...,Y

(n)

)





∂N

∂Y







,...,Y

(n)

)



+ ...+



∂N

∂Y

(n)





,...,Y

(n)

)

(n)

= −L [Y

+ Y

, Y



+ Y



,...,Y

(n)

+ Y

(n)

] − N[Y

+ Y

, Y



+ Y



,...,Y

(n)

+ Y

(n)

] (24)

where the partial derivatives inside square brackets in equation (24) represent Jacobian

matrices deﬁned as in equation (20) with i

= 2.

After solving (24), the current (2nd order) estimate of the solution Y

(x) is

(x) ≈ Y

(x)+Y

(x). (25)

Next we deﬁne Z

(x) (see Figure 3) such that

(x)=Z

(x)+Y

(x). (26)

Equation (26) is substituted in the non-linear equation (23) and the linearisation process

described above is repeated. This process is repeated for m

= 3,4,5,...,i. In g eneral, we

have

(x)=Z

i+1

(x)+Y

(x). (27)

Thus, Y

(x) is obtained as

(x)=Z

(x)+Y

(x), (28)

= Z

(x)+Y

(x), (29)

= Z

(x)+Y

(x), (30)

= Z

i+1

(x)+Y

(x)+...+ Y

(x)+Y

(x), (31)

= Z

i+1

(x)+

∑

m=0

(x). (32)

The procedure for obtaining each Z

(x) is illustrated in Figures 1, 2 and 3 respectively for

= 1, 2, 3.

331

Soret and Dufour Effects on Steady MHD Natural Convection Flow Past

a Semi-Infinite Moving Vertical Plate in a Porous Medium with Viscous Dissipation ...

8 Mass Transfer

3,1

1,1

2,1

1,0

(

)

= y

(x)

Fig. 3. Geometric representation of the functions z

3,1

We note that when i becomes large, Z

i+1

becomes increasingly smaller. Thus, for large i,we

can approximate the ith order solution of Y

(x) by

(x)=

∑

m=0

(x)=Y

(x)+

i−1

∑

m=0

(x). (33)

Starting from a known initial guess Y

(x), the solutions for Y

(x) can be obtained by

successively linearising the governing equation (11) and solving the resulting linear equation

for Y

(x) given that the previous guess Y

i−1

(x) is known. The general form of the linearised

equation that is successively solved for Y

(x) is given by

, Y



, Y



,...,Y

(n)

]+a

0,i−1

(n)

+ a

1,i−1

(n−1)

+ ...+ a

n−1,i−1



+ a

n,i−1

= R

i−1

(x),

(34)

where

0,i−1

(x)=

⎡

⎣

∂N

∂Y

(n)

⎤

⎦



i−1

∑

m=0

i−1

∑

m=0



i−1

∑

m=0



,...,

i−1

∑

m=0

(n)



(35)

1,i−1

(x)=

⎡

⎣

∂N

∂Y

(n−1)

⎤

⎦



i−1

∑

m=0

i−1

∑

m=0



i−1

∑

m=0



,...,

i−1

∑

m=0

(n)



(36)

n−1,i−1

(x)=



∂N

∂Y







i−1

∑

m=0

i−1

∑

m=0



i−1

∑

m=0



,...,

i−1

∑

m=0

(n)



(37)

332

Evaporation, Condensation and Heat Transfer

Soret and Dufour Effects on Steady MHD Natural Convection Flow Past a Semi-Inﬁnite Moving Vertical Plate in a Porous Medium with Viscous Dissipation in the Presence of

a Chemical Reaction 9

n,i−1

(x)=



∂N

∂Y





i−1

∑

m=0

i−1

∑

m=0



i−1

∑

m=0



,...,

i−1

∑

m=0

(n)



(38)

i−1

(x)=−L



i−1

∑

m=0

i−1

∑

m=0



i−1

∑

m=0



,...,

i−1

∑

m=0

(n)



− N



i−1

∑

m=0

i−1

∑

m=0



i−1

∑

m=0



,...,

i−1

∑

m=0

(n)



. (39)

4. Numerical solution

In this section we solve the governing equations (7 - 9 ) using the SLM method described in

the last section. We begin by writing the governing equations (7 - 9) as a sum of the linear and

nonlinear components as

− L[ f , f



, f



, f



, θ, θ



, θ



, φ, φ



, φ



]+N[ f , f



, f



, f



, θ, θ



, θ



, φ, φ



, φ



]=0, (40)

where the primes denote differentiation with respect to η and

L[ f , f



, f



, f



, θ, θ



, θ



, φ, φ



, φ



⎡

⎣

⎤

⎦

⎡

⎣



− (M + Ω) f



+ Gr θ + Gmφ



+ Duφ



+ Srθ



− γφ

⎤

⎦

(41)

[ f , f



, f



, f



, θ, θ



, θ



, φ, φ



, φ



⎡

⎣

⎤

⎦

⎡

⎣



− ( f



)

f θ



+ Ec( f



)

f φ



⎤

⎦

. (42)

Using equation (34), the general equation to be solved for Y

,where

⎡

⎣

⎤

⎦

, (43)

, Y



, Y



, Y



]+a

0,i−1



+ a

1,i−1



+ a

2,i−1



+ a

3,i−1

= R

i−1

(η), (44)

subject to the boundary conditions

(0)= f



(0)=θ

(0)=φ

(0)= f



(∞)=θ

(∞)=φ

(∞)=0. (45)

where

0,i−1

⎡

⎢

⎣

∂N

∂ f



∂N

∂θ



∂N

∂φ



∂N

∂ f



∂N

∂θ



∂N

∂φ



∂N

∂ f



∂N

∂θ



∂N

∂φ



⎤

⎥

⎦

⎡

⎣

000

⎤

⎦

(46)

1,i−1

⎡

⎢

⎣

∂N

∂ f



∂N

∂θ



∂N

∂φ



∂N

∂ f



∂N

∂θ



∂N

∂φ



∂N

∂ f



∂N

∂θ



∂N

∂φ



⎤

⎥

⎦

⎡

⎣

∑

2Ec

∑



000

⎤

⎦

(47)

333

Soret and Dufour Effects on Steady MHD Natural Convection Flow Past

a Semi-Infinite Moving Vertical Plate in a Porous Medium with Viscous Dissipation ...

10 Mass Transfer

2,i−1

⎡

⎢

⎣

∂N

∂ f



∂N

∂θ



∂N

∂φ



∂N

∂ f



∂N

∂θ



∂N

∂φ



∂N

∂ f



∂N

∂θ



∂N

∂φ



⎤

⎥

⎦

⎡

⎣

−2

∑



∑

⎤

⎦

(48)

3,i−1

⎡

⎢

⎣

∂N

∂ f

∂N

∂θ

∂N

∂φ

∂N

∂ f

∂N

∂θ

∂N

∂φ

∂N

∂ f

∂N

∂θ

∂N

∂φ

⎤

⎥

⎦

⎡

⎣

∑



∑



∑



⎤

⎦

(49)

i−1

⎡

⎣

1,i−1

2,i−1

3,i−1

⎤

⎦

1,i−1

= −



∑



− (M + Ω)

∑



+ Gr

∑

+ Gm

∑



−



∑







(50)

2,i−1

= −



∑



+ Du

∑



∑



+ Ec



∑







(51)

3,i−1

= −



∑



+ Sr

∑



− γ

∑





(52)

and the sums in equation (46 - 52) denote

∑

i−1

∑

m=0

.Onceeachsolutionforf

, θ

, φ

(i ≥ 1) has

been found from iteratively solving equations (44 - 45), the approximate solutions for f

(η),

(η) and φ(η) are obtained as

(η) ≈

∑

m=0

(η), (53)

(η) ≈

∑

m=0

(η), (54)

(η) ≈

∑

m=0

(η), (55)

where i is the order of SLM approximation. Since the coefﬁcient parameters and the right

hand side of equations (44), for i

= 1,2,3,..., are known (from previous iterations). The

equation system can easily be solved using numerical methods such as ﬁnite differences,

ﬁnite elements, Runge-Kutta based shooting methods or collocation methods. In this work,

equations (44) are solved using the Chebyshev spectral collocation method. This method is

based on approximating the unknown functions by the Chebyshev interpolating polynomials

in such a way that they are collocated at the Gauss-Lobatto points deﬁned as

= cos

πj

, j

= 0, 1, . . . , N, (56)

where N

+ 1 is the number of collocation points used (see for example Canuto et al. (1988);

Don & Solomonoff (1995); Trefethen (2000)). In order to implement the method, the physical

334

Evaporation, Condensation and Heat Transfer

Soret and Dufour Effects on Steady MHD Natural Convection Flow Past a Semi-Inﬁnite Moving Vertical Plate in a Porous Medium with Viscous Dissipation in the Presence of

a Chemical Reaction 11

region [0, ∞) is transformed into the region [−1, 1] using the domain truncation technique in

which the problem is solved on the interval

[0, L] instead of [0, ∞). This leads to the mapping

ξ + 1

−1 ≤ ξ ≤ 1 (57)

where L is the scaling parameter used to invoke the boundary condition at inﬁnity. The

unknown functions f

, θ

and φ

are approximated at the collocation points by

(ξ) ≈

∑

k=0

(ξ

), (58)

(ξ) ≈

∑

k=0

(ξ

), (59)

(ξ) ≈

∑

k=0

(ξ

), (60)

= 0, 1, . . . , N, (61)

where T

is the kth Chebyshev polynomial deﬁned as

(ξ)=cos[k cos

−1

(ξ)]. (62)

The derivatives of the variables at the collocation points are represented as

dη

∑

k=0

(ξ

dη

∑

k=0

(ξ

dη

∑

k=0

(ξ

), j = 0, 1, . . . , N (63)

where a is the order of differentiation and D

D with D being the Chebyshev spectral

differentiation matrix (see for example, Canuto et al. (1988); Trefethen (2000)). Substituting

equations (57 - 63) in (44) - (45) leads to the matrix equation given as

i−1

= R

i−1

, (64)

subject to the boundary conditions

(ξ

∑

k=0

(ξ

∑

k=0

(ξ

)=θ

(ξ

)=θ

(ξ

)=φ

(ξ

)=φ

(ξ

)=0 (65)

where

i−1

= A + a

1,i−1

+ a

2,i−1

+ a

3,i−1

(66)

⎡

⎣

− (M + Ω)D GrI GmI

DuD

O SrD

− γI

⎤

⎦

(67)

⎡

⎣

DOO

ODO

OOD

⎤

⎦

(68)

335

Soret and Dufour Effects on Steady MHD Natural Convection Flow Past

a Semi-Infinite Moving Vertical Plate in a Porous Medium with Viscous Dissipation ...

12 Mass Transfer

and Y

and R

i−1

are (3N + 1) × 1 column vectors deﬁned by

⎡

⎣

⎤

⎦

, R

i−1

⎡

⎣

1,i−1

2,i−1

3,i−1

⎤

⎦

, (69)

where

=[f

(ξ

), f

(ξ

),...,f

(ξ

N−1

), f

(ξ

)]

, (70)

=[θ

(ξ

), θ

(ξ

),...,θ

(ξ

N−1

), θ

(ξ

)]

, (71)

=[φ

(ξ

), φ

(ξ

),...,φ

(ξ

N−1

), φ

(ξ

)]

, (72)

1,i−1

=[r

1,i−1

(ξ

), r

1,i−1

(ξ

),...,r

1,i−1

(ξ

N−1

), r

1,i−1

(ξ

)]

, (73)

2,i−1

=[r

2,i−1

(ξ

), r

2,i−1

(ξ

),...,r

2,i−1

(ξ

N−1

), r

2,i−1

(ξ

)]

, (74)

3,i−1

=[r

3,i−1

(ξ

), r

3,i−1

(ξ

),...,r

3,i−1

(ξ

N−1

), r

3,i−1

(ξ

)]

, (75)

In the above deﬁnitions, a

k,i −1

,(k = 1, 2, 3) are now diagonal matrices of size 3(N + 1) ×

3(N + 1) and the superscript T is the transpose.

To impose the boundary conditions (65) on equation (64) we begin by splitting the matrix M

in equation (64) into 9 blocks each of size

(N + 1) × (N + 1) in such a way that M takes the

form

i−1

⎡

⎣

⎤

⎦

(76)

We then modify the ﬁrst and last rows of M

(m, n = 1, 2, 3) and r

m,i−1

and the N − 1th row

of M

1,1

, M

1,2

, M

1,3

in such a way that the modiﬁed matrices M

i−1

and R

i−1

take the form;

i−1

⎛

⎜

⎝

0,0

0,1

··· D

0,N−1

0,N

00··· 0000··· 00

N,0

N,1

··· D

N,N−1

N,N

00··· 0000··· 00

··· 0100··· 0000··· 00

00··· 0010··· 0000··· 00

00··· 0000··· 0100··· 00

00··· 0000··· 0010··· 00

00··· 0000··· 0000··· 01

⎞

⎟

⎠

, (77)

336

Evaporation, Condensation and Heat Transfer

Soret and Dufour Effects on Steady MHD Natural Convection Flow Past a Semi-Inﬁnite Moving Vertical Plate in a Porous Medium with Viscous Dissipation in the Presence of

a Chemical Reaction 13

i−1

⎛

⎜

⎝

1,i−1

(ξ

)

1,i−1

(ξ

N−2

)

2,i−1

(ξ

)

2,i−1

(ξ

N−2

)

2,i−1

(ξ

N−1

)

3,i−1

(ξ

)

3,i−1

(ξ

N−2

)

3,i−1

(ξ

N−1

)

⎞

⎟

⎠

(78)

After modifying the matrix system (64) to incorporate boundary conditions, the solution is

obtained as

= M

−1

i−1

. (79)

5. Results and discussion

In this section we present numerical calculations for different values of M, Gr, Gm, γ, Du,

and f

for ﬁxed values of Ω = 1, and Re = 1 to obtain a clear insight of the physical

problem. In computing the numerical results presented in this paper, unless otherwise stated,

the following values of physical parameters were used: M

= 1, Ω = 1, Gr = 1, Gm = 1,

= 0.71, Sc = 0.6, Sr = 0.1, γ = 1, Ec = 1, f

= 0, Du = 0.1. The numerical results are

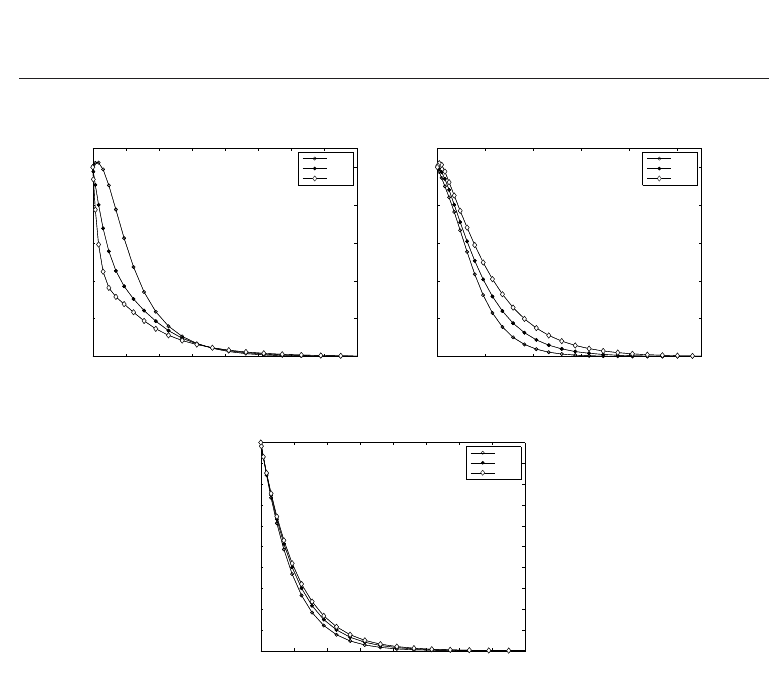
displayed graphically. The effect of the Hartmann number M on the dimensionless velocity



(η), temperature θ(η) and concentration φ(η) proﬁles are respectively represented in Figs

(a), (b) and (c). It is observed in these Figs, that the velocity decreases with the increase of

the magnetic parameter, the value of the temperature proﬁles increase with the magnetic

parameter. The concentration of the ﬂuid have a small increase with the increase of the

magnetic parameter. The effects of a transverse magnetic ﬁeld give rise to a resistive-type

force called the Lorentz force. This force has the tendency to slow down the motion of the

ﬂuid ﬂow and to increase its thermal boundary layer hence increasing the temperature of the

ﬂuid ﬂow.

Figure (d), (e) and (f) depict the effects of varying the local thermal free convection

(Gr) with

increasing η on the dimensionless velocity, temperature and concentration. It is observed in

Fig (d) that the increase of the Grashof number leads to the increase of the velocity of the ﬂuid.

This is because the increase of Gr results in the increase of temperature gradients

∞

− T

∞

leads to the enhancement of the velocity due to the enhanced convection. From Fig (e) we

observe that the effect of increasing the values of thermal free convection is to reduce the

temperature proﬁles

(θ). We also observe in Fig (f) that the concentration proﬁles decrease

337

Soret and Dufour Effects on Steady MHD Natural Convection Flow Past

a Semi-Infinite Moving Vertical Plate in a Porous Medium with Viscous Dissipation ...

14 Mass Transfer

0 1 2 3 4 5 6 7 8

0.2

0.4

0.6

0.8



(η)

M = 0

M = 2

M = 4

(a) Plot of f



( η) for varying M

0 2 4 6 8 10

0.2

0.4

0.6

0.8

θ(η)

M = 0

M = 2

M = 4

(b) Plot of θ(η) for varying M

0 1 2 3 4 5 6 7 8

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

φ(η)

M = 0

M = 2

M = 4

as the Grashof number increases. It can be clearly seen that the effect of Grashof number

(Gr) is to decrease the concentration distribution as the concentration distribution species is

dispersed away largely due to increased temperature gradient. The modiﬁed Grashof number

Gm has the same effect as the local Grashof number

(Gr) on the ﬂow properties as depicted

in Figs (g), (h) and

(i).

Figs (j)-(l) depict the effects of the chemical reaction parameter γ on the dimensionless velocity,

temperature and concentration distributions. The effect of chemical reaction parameter is

very important in the concentration ﬁeld. Chemical reaction increases the rate of interfacial

mass transfer. Reaction reduces the local concentration, thus increases its concentration

gradient and its ﬂux. Figs (m)- (o) show the inﬂuence of the Eckert number Ec,onthe

velocity, temperature and concentration proﬁles, respectively. By analyzing these Figs, it

is clearly revealed that the effect of Eckert number is to increase both the velocity and the

temperature distributions in the ﬂow region. This is due to the fact that the heat energy is

stored in liquid due to the frictional heating. Thus the effect of increasing Ec is to enhance

the temperature at any point as well as the velocity. However, the Eckert number Ec has

no signiﬁcant effect on the concentration within the ﬂow region. Figs (p) - (r) depict the

inﬂuence of the Dufour parameter

(Du) on the dimensionless velocity, temperature and

concentration distributions. It can be clearly seen from Fig (p) that as the Dufour effects

338

Evaporation, Condensation and Heat Transfer