Alexandrov A.S.,Theory of Superconductivity - From Weak to Strong Coupling

Подождите немного. Документ загружается.

156

Strong-coupling theory

F

7

DUELWUDU\

XQLWV

%(&

%&6

77



Figure 4.13. BEC critical ﬁeld of a CBG compared with the H

(T ) of BCS

superconductors.

bipolaron binding energy  is much larger than their T

. Bosons are condensed

at T = 0 no matter what their energy spectrum is. Hence, in the CBG model,

(0) =∞(ﬁgure 4.13). For composed bosons, like bipolarons, the pair-

breaking limit is given by µ

(0) ≈ ,sothatH

(0)  H

4.7.9 Symmetry of the order parameter

The anomalous Bogoliubov average



, r

) =

)



)

is the superconducting order parameter both in the weak- and strong-coupling

regimes. It depends on the relative coordinate ρ = r

− r

of two electrons

of the pair and on the centre-of-mass coordinate R = (r

+ r

)/2. Hence, its

Fourier transform, f (k, K ), depends on the relative momentum k and on the

centre-of-mass momentum, K. In the BCS theory, K = 0 (in a homogeneous

superconductor) and the Fourier transform of the order parameter is proportional

to the gap in the quasi-particle excitation spectrum, f (k, K )



(section 2.2).

Hence, the symmetry of the order parameter and the symmetry of the gap are the

same in the weak-coupling regime. Under the rotation of the coordinate system,



changes its sign if the Cooper pairing is unconventional (section 2.10). In this

case, the BCS quasi-particle spectrum is gapless.

In the bipolaron theory, the symmetry of the BEC is not necessarily the

same as the ‘internal’ symmetry of a pair [123]. While the latter describes the

transformation of f (k, K ) with respect to the rotation of k, the former (‘external’)

symmetry is related to the rotation of K . Therefore, it depends on the bipolaron

band dispersion but not on the symmetry of the bound state. As an example, let

us consider a tight-binding bipolaron spectrum comprising two bands on a square

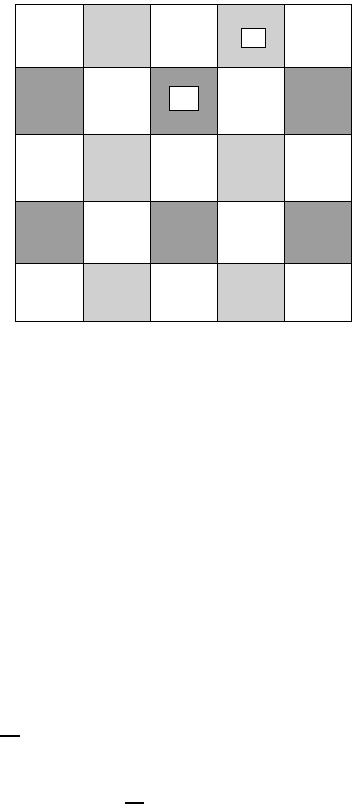
Bipolaronic superconductivity

157











Figure 4.14. d-wave condensate wavefunction, in the Wannier representation. The order

parameter has different signs in the shaded cells and is zero in the blank cells.

lattice with the period a = 1:

= t cos(K

) − t



cos(K

) (4.269)

=−t



cos(K

) + t cos(K

They transform into one another under π/2 rotation. If t, t



> 0, ‘x’ bipolaron

band has its minima at K = (±π, 0) and the y-band at K = (0, ±π).These

four states are degenerate, so that the condensate wavefunction ψ

(m) in the site

space, m = (m

, m

), is given by

(m) = N

−1/2



K=(±π,0),(0,±π)

−iK ·m

. (4.270)

where b

=±

√

are c-numbers at T = 0. The superposition (4.270) respects

the time-reversal and parity symmetries, if

(m) =

√

[cos(πm

) ± cos(πm

)]. (4.271)

The two order parameters (equation (4.271)) are physically identical because

they are related by the translation transformation, ψ

, m

) = ψ

−

, m

1). Both have a d-wave symmetry-changing sign, when the lattice is rotated by

π/2 (ﬁgure 4.14). The d-wave symmetry is entirely due to the bipolaron energy

dispersion with four minima at K = 0. When the bipolaron spectrum is not

degenerate and its minimum is located at the  point of the Brillouin zone, the

condensate wavefunction is s-wave with respect to the centre-of-mass coordinate.

The symmetry of the gap has little to do with the symmetry of the order parameter

in the strong-coupling regime. The one-particle excitation gap is half of the

158

Strong-coupling theory

bipolaron binding energy, /2, and does not depend on any momentum in zero

order of the polaron bandwidth, i.e. it has an ‘s’-wave symmetry. In fact, due

to a ﬁnite dispersion of polaron and bipolaron bands (sections 4.3 and 4.6), the

one-particle gap is an anisotropic s-wave. A multi-band electron structure can

include bands only weakly coupled with phonons which could overlap with the

bipolaronic band (see also part 2). In this case, the CBG coexists with the Fermi

gas just as

He bosons coexist with

He fermions in the mixture of He-4 and He-3.

The one-particle excitation spectrum of such mixtures is gapless.

PART 2

APPLICATIONS TO HIGH-T

SUPERCONDUCTORS

Chapter 5

Competing interactions in unconventional

superconductors

5.1 High-T

superconductors: different concepts

Nowadays there are many complex high-T

superconductors including copper

[1, 127] and a few other oxides, doped fullerenes M

[128, 129] (M is an

alkali metal) and the more recently discovered magnesium diborade MgB

[130]

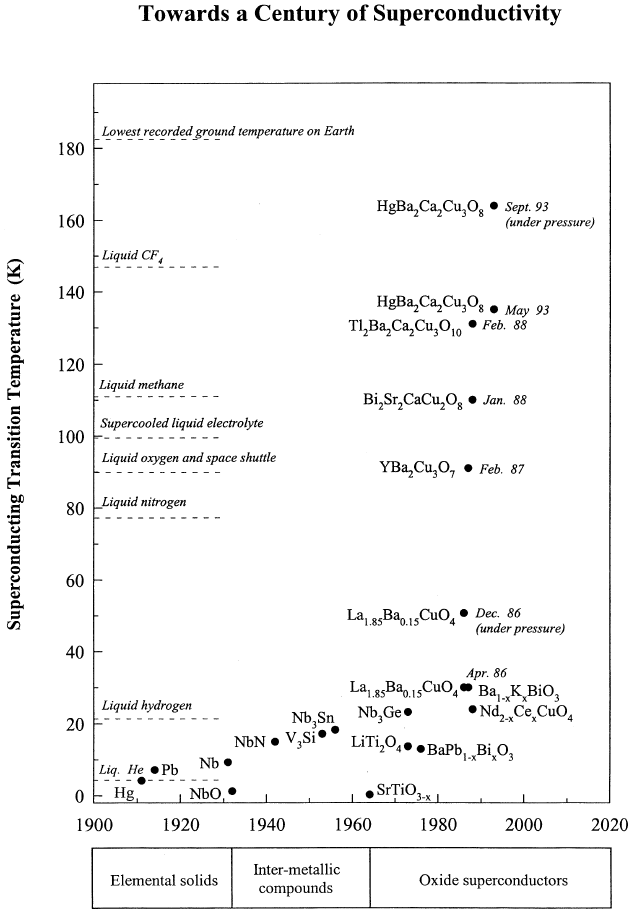
with a critical temperature above 30 K, ﬁgure 5.1.

These discoveries have broken all constraints on the maximum T

predicted

by conventional theory of low-temperature superconducting metals and their

alloys. As highlighted by Simon [132], the canonical theory has not provided

a ‘materials’ aspect in the search for new high-T

superconductors. Nevertheless,

in a phenomenological sense, any superconductivity can just be treated as a

consequence of the formation of pairs and their condensation—even within the

BCS framework, as was noted by Ginzburg [133] in 1968 (chapter 1). At any

value of the e–ph interaction superconductivity is a correlated many-body state of

pairs which is well described by BCS theory in the weak-coupling regime λ  1,

where pairing takes place in the momentum space due to the Pauli exclusion

principle (collective pairing) and by the bipolaron theory in the strong coupling

regime, λ

1, where pairing is individual (upper half-plane in ﬁgure 5.2). Hence,

knowledge of the carrier-pairing mechanism and of the nature of the normal state

is central to an understanding of high-T

supeconductivity.

In general, the bosonic ﬁeld, which ‘glues’ two carriers together, can not only

be ‘phononic’, as in BCS and bipolaron theory, but also ‘excitonic’ [133, 134],

‘plasmonic’ [135, 136] and/or of magnetic origin [137, 138]. BCS theory like

any mean-ﬁeld theory is rather universal, so that it describes the cooperative

quantum phenomenon of superconductivity well even with these non-phononic

attraction mechanisms, if the coupling is weak (see left-hand side of ﬁgure 5.2).

If the coupling is strong, magnetic interaction could result in the spin–bipolaron

formation as suggested by Mott [139]. The main motivation behind these concepts

161

162

Competing interactions in unconventional superconductors

Figure 5.1. Towards a century of superconductivity. A plot of the evolution of the

superconducting transition temperature, from 1911, to the present situation. We also

include the characteristic temperatures of a variety of cryogenic liquids, as well as the

lowest recorded ground temperature on Earth (−89.2

◦

C) [131].

High-

superconductors: different concepts

163

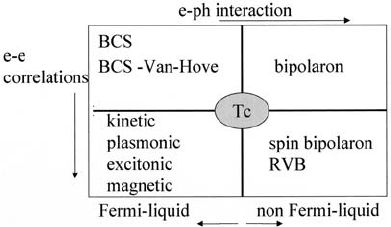
Figure 5.2. BSC-like theories of high-T

superconductors with the electron–phonon (top)

and electron–electron (bottom) interactions (left-hand side). Right-hand side: non-Fermi

liquid theories with electron–phonon (top) and electron–electron (bottom) correlations.

is that high T

might be achieved by replacing low-frequency acoustic phonons

in conventional BCS theory by higher-frequency bosonic modes, such as the

electron plasmon (chapter 3) or by spin waves (pseudomagnons). However, the

Coulomb pseudopotential creates a serious problem for any of these non-phononic

mechanisms. With the increasing energy scale of the bosonic ﬁeld, the retardation

of the effective attraction vanishes and the Tolmachev logarithm (section 3.5)

cannot be applied. Then the direct Coulomb repulsion would deﬁnitely prevent

any pairing in these models because the exchange electron–electron interaction is

always weaker than direct repulsion. The problem is particularly grave in novel

superconductors, where the carrier density is low, and the screening of the direct

Coulomb repulsion is poor.

Therefore, some authors [140, 141] dogmatized that the interaction in novel

superconductors is essentially repulsive and unretarded and that it also provides

high T

without any phonons. A motivation for this concept can be found

in the earlier work by Kohn and Luttinger [57], who showed that the Cooper

pairing of repulsive fermions is possible. But the same work clearly showed

that the T

of repulsive fermions is extremely low, well below the mK scale

(section 3.6). Nevertheless, BCS and BCS-like theories (including the Kohn–

Luttinger consideration) rely heavily on the Fermi-liquid model of the normal

state. This model fails in many high-temperature superconductors (chapter 6).

There are no obvious apriorireasons for discarding the dogma, if the normal

state is not the Fermi liquid. There is little doubt that strong on-site repulsive

correlations (Hubbard U) are an essential feature of the cuprates. Indeed all

undoped parent compounds are insulators with an insulating gap of about 2 eV

or so. But if the repulsive correlations are weak, one would expect a metallic

behaviour for the half-ﬁlled d-band of copper in cuprates or, at most, a much

smaller gap caused by lattice and spin distortions (i.e. due to charge and/or spin

density waves [142]). Therefore, it is the strong on-site repulsion of d-electrons

in cuprates which results in their parent ‘Mott’ insulating state (section 5.2).

164

Competing interactions in unconventional superconductors

Differing from conventional band-structure insulators with completely ﬁlled or

empty Bloch bands, the Mott insulator arises from a potentially metallic half-ﬁlled

band due to the Coulomb blockade of electron tunnelling to neighbouring sites,

if U > zT(a) [143]. The insulator is antiferromagnetic with one hole and spin-

per site. In using this model, we have to realize that the insulating properties of

the Mott insulator do not depend on the ordering of the spins; they persist above

the N´eel temperature and arise because the on-site Coulomb repulsion is larger

than the half-bandwidth.

When on-site correlations are strong and dimensionality is low, there is an

alternative to the usual Fermi-liquid description proposed by Anderson [140].

In Anderson’s resonating-valence-bond (RVB) theory, the ground state supports

‘topological solitons’ (the so-called spinons and holons), such as occur in one-

dimensional models like the one-dimensional Hubbard model (see later). The

main idea is that an electron injected into a two-dimensional layer decays

into a singlet charge e component (holon) and a spin-

component (spinon)

and, conversely, must form again in order to come out. This is the case

for one-dimensional repulsive electrons, which form the so-called Luttinger

liquid in one dimension. Bose quasi-particles imply a condensate. However,

there is no experimental evidence for a charge e superﬂuid. Therefore, in

the so-called interlayer RVB extension of the model [144], it was suggested

that the superconductivity of copper-based high-T

materials is due to holon-

pair tunnelling between the copper–oxygen planes. There is no single-particle

coherent tunnelling between two spinon–holon planes above T

.However,

there is a coherent two-particle tunnelling between them below T

. Then the

corresponding kinetic energy should be responsible for the BCS-like pairing at

temperatures below T

≈ t

⊥

/t and for the plasma-like gap, observed in the c-

axis conductivity. Here t and t

⊥

are the in-plane and out-of-plane renormalized

hopping integrals, respectively. Anderson argued that the existence of the upper

Hubbard band (section 5.2) would necessarily lead to the Luttinger liquid even in

two dimensions, as opposed to the Fermi liquid. While the interlayer RVB model

was found to be incompatible with experiments [145], the basic idea of spin and

charge separation had been worked out in great detail [146]. The microscopic

Hubbard Hamiltonian [147]

H = T (a)



mn,s

†

+ H.c.]+U



ˆn

m↑

ˆn

m↓

(5.1)

was proposed to justify the RVB concept, where mn are the nearest neigbours.

The Hamiltonian describes the antiferromagnetic Mott insulator at half ﬁlling

when U > D. In the strong correlation limit, U  T (a), the doubly occupied

sites take a large Coulomb energy and the Hubbard Hamiltonian can be reduced

to the so-called t–J model [148]

H = T (a)



mn,s

[˜c

†

˜c

+ H.c.]+J



mn

(

−

ˆn

) (5.2)

High-

superconductors: different concepts

165

where the projected electron operators ˜c

m↑

= c

m↑

(1 −ˆn

m↓

) act in the subspace

without double occupancy, ˆn

=ˆn

m↑

+ˆn

m↓





˜c

†

(τ

)



˜c



are three components of the on-site spin-

operator (α = 1, 2, 3) and τ

are the

Pauli matrices as in equation (3.73). The second term in

H describes the spin-

Heisenberg antiferromagnet with the exchange energy

J =

(a)

(5.3)

for the nearest neigbours. The exchange energy leads to spin polarons similar to

lattice polarons but dressed with magnetic ﬂuctuations rather than with phonons.

However, the non-fermionic commutation relations for the projected electron

operators lead to an additional kinematic interaction between carriers doped into

the Mott insulator. As a result an analytical solution of the t–J model is a very

hard problem but not in the dilute limit. In this limit a doped hole dressed by

antiferromagnetic spin ﬂuctuations propagates coherently in a narrow band of

the order of J  T (a) like a small polaron. One could believe that the same

spin ﬂuctuations, which dress a single hole, mediate a superconducting pairing of

spin polarons due to an effective attractive interaction of the order of J .Tobe

consistent with the N´eel temperature of parent undoped cuprates and with their

spin-wave excitation spectrum, J should be of the order of 0.1 eV. The magnetic

singlet pairing might be effective in the d-channel (section 2.10), where the

direct Coulomb repulsion is diminished due to the d-wave symmetry of the BCS

order parameter 

. The possibility of d-wave BCS-like superconductivity in

the two-dimensional Hubbard model near half-ﬁlling was suggested by Scalapino

et al [149] concurrently with the discovery of novel superconductors. There is

now a variety of phase-sensitive experiments, which support the unconventional

symmetry of the order parameter in some cuprates, while other experiments

appear to contradict this symmetry (see section 8.2).

Independent of any experimental evidence, the Hubbard U and t–J models

share an inherent difﬁculty in determining the order. While some groups

claimed that they describe high-T

superconductors at ﬁnite doping, other authors

could not ﬁnd any superconducting instabilty without an additonal (i.e. e–ph)

interaction [150]. Therefore, it has been concluded that models of this kind

are highly conﬂicting and confuse the issue by exaggerating the magnetism

rather than clarifying it [151]. In our view [12], the problem with the RVB-like

concepts of high-T

is that for them to be valid, the diffractive scattering between

holes of cuprate superconductors needs to be absent. A known case where

diffractive scattering is absent is that of one-dimensional interacting fermion

systems. But in one-dimensional interacting fermion systems the scattering is

non-diffractive due to topological reasons. In two and higher dimensions, one