Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems
Подождите немного. Документ загружается.


B IFURCATIONS
point at x ⫽ (⫺1 ⫹
3) 2. The case in which a pair of fixed points appear in
a region where there were none, as a parameter is varied, is called a saddle-node
bifurcation.
At a saddle-node bifurcation, two fixed points of f
a
, one stable and one
unstable, are born as the parameter a is increased. Of course, this is a matter of
perspective. Alternatively, we could say that the two fixed points disappear as a is
decreased. The term “saddle-node” derives from this type of bifurcation in a two-
dimensional state space, where the unstable orbit is a saddle and the stable orbit
is an attractor or “node”. For maps in which the state space is one-dimensional,
this bifurcation is also sometimes called a tangent bifurcation. This name comes
from the fact that the derivative f
a
at a fixed point saddle-node bifurcation orbit
must be ⫹1, and thus the graph must be tangent to the line y ⫽ x, as we discuss
later.
Figure 11.1 shows plots of the state space graphed against itself before,
during, and after the bifurcation value. A different type of plot compresses the
state space information so that variation as a function of the parameter a can
be viewed. This type of graph, exemplified by Figure 11.2, is called a bifurcation
diagram. The vertical axis corresponds to the state space. Only significant points
in the state space are plotted.
-2
-1
0
1
2
-1 0 1 2
x
a
o
o
(-1/4,-1/2)
(3/4,1/2)
Figure 11.2 Bifurcation diagram of a saddle-node bifurcation.
Fixed points of the quadratic family f(a, x) ⫽ a ⫺ x
2
are shown. Attracting fixed
points (sinks) are denoted by the solid curve, and repelling fixed points (sources) are
on the dashed curves. The circle at a ⫽⫺1 4 denotes the location of a saddle-node
bifurcation. The other circle denotes where a period-doubling bifurcation occurs.
450

11.1 SADDLE-NODE AND P ERIOD-DOUBLING B IFURCATIONS
Figure 11.2 depicts the fixed points of f
a
as a function of a near the saddle
node. Attracting fixed points are shown on the solid curve and repelling fixed
points are on the dashed curves. For example, when a ⫽ 0, the function f has two
fixed points, one an attractor and one a repeller.
There are more bifurcations hiding in Figure 11.2. Notice that the point
(
3
4
,
1
2
) represents a passage of the curve of fixed points from solid to dashed
indicating a change in stability. How do the fixed points lose their stability?
Recall that if the derivative f
a
evaluated at a fixed point satisfies |f
a
| ⬍ 1, then
the fixed point is an attractor, and if |f
a
| ⬎ 1, then it is a repeller. Clearly, the
way fixed points change stability is to have f
a
(x) move across the border ⫾1as
the parameter a varies. As a increases from ⫺1 4to3 4, the derivative of f
a
at
the attracting fixed point decreases from ⫹1to⫺1. For a ⬎ 3 4, the derivative
of f
a
at this fixed point has crossed the ⫺1 border, and the fixed point becomes a
repeller. In the parameter range (
3
4
,
⬁
), the map f
a
has no fixed-point attractors.
However, f
a
does have a period-two attractor for a in (
3
4
,
5
4
). At a ⫽ 3 4,
the two points in this orbit split off from the fixed point x ⫽
1
2
. For a slightly
larger than
1
2
, one point in the orbit is greater than
1
2
and one is less than
1
2
.
This bifurcation is called a period-doubling bifurcation (or, sometimes, a flip
bifurcation). In Figure 11.3 the graph of f
a
is shown for a values before, at, and
following the period-doubling bifurcation.
-2
-1
0
1
2
-2 -1 0 1 2
-2
-1
0
1
2
-2 -1 0 1 2
-2
-1
0
1
2
-2 -1 0 1 2
(a) (b) (c)
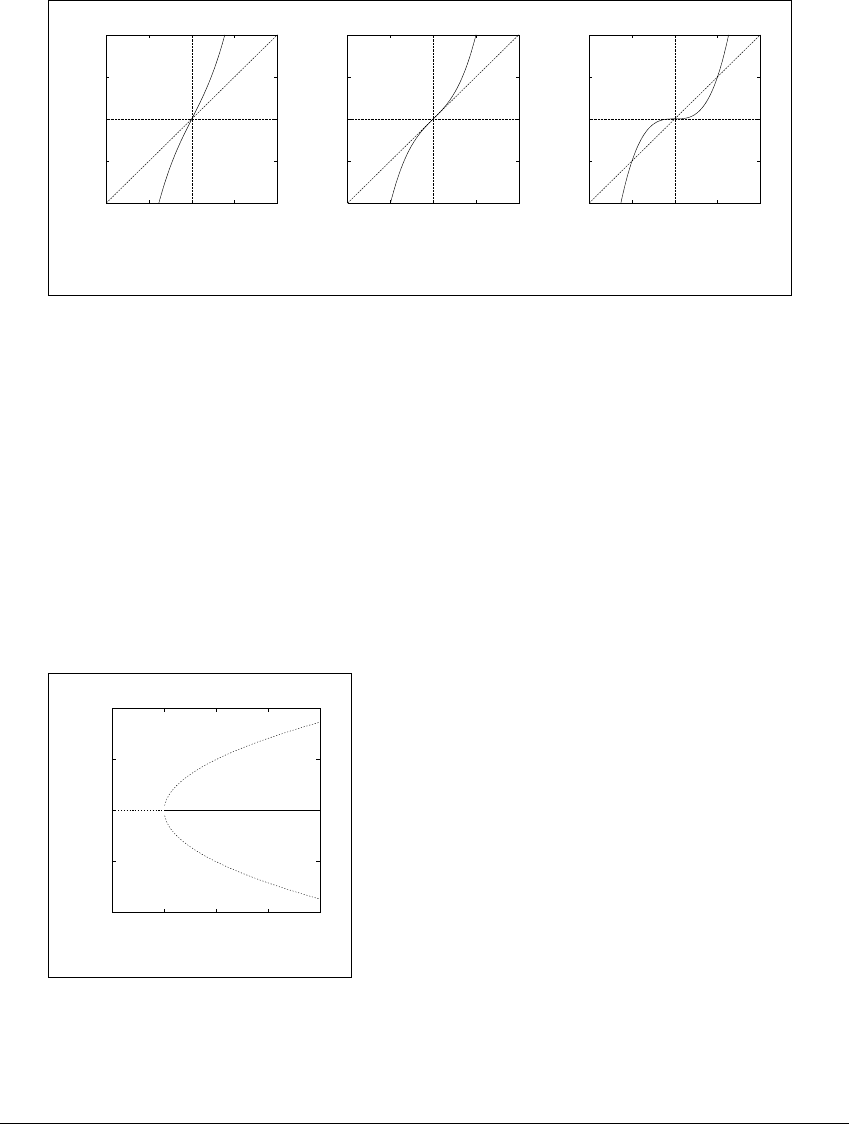
Figure 11.3 The quadratic map at a period-doubling bifurcation.
Graphs of the quadratic family f
a
(x) ⫽ a ⫺ x
2
before, during and after a period-
doubling bifurcation. (a) a ⫽ 0.5. Orbits flip back and forth around the sink as
they approach. (b) a ⫽ 0.75. At the bifurcation point, x ⫽ 1 2 still attracts orbits,
although the derivative of f
a
is ⫺1. (c) a ⫽ 1. Beyond the bifurcation, orbits are
attracted by the period-two sink.
451
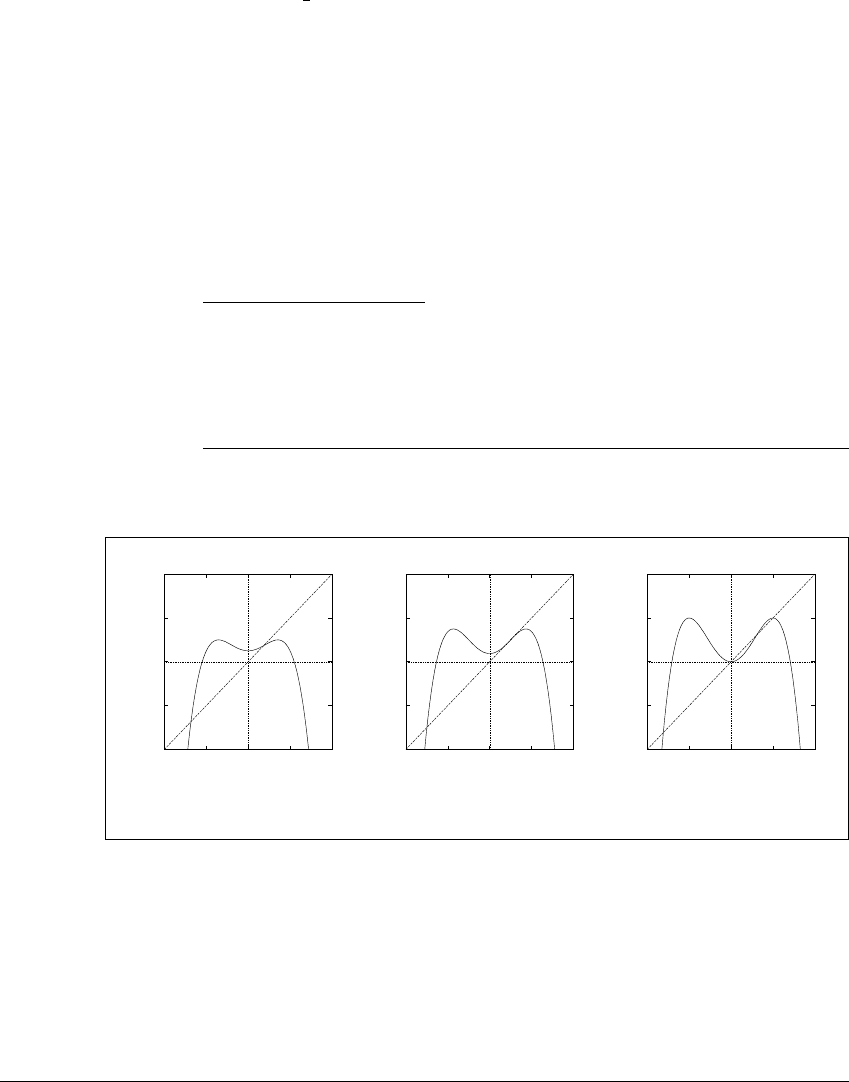
B IFURCATIONS
Since the derivative at the (positive) fixed point is negative for parameter
values near
3
4
, iterates of points near the fixed point flip back and forth around
the fixed point. We can observe this flipping in the cobweb plot (Figures 11.3(a)
and (c)). The fixed point, which is unstable after the bifurcation, is called a flip
repeller since its derivative is smaller than ⫺1. A fixed point with derivative
greater than ⫹1 is called a regular repeller. (Compare these definitions with
those of “flip saddle” and “regular saddle” in Chapter 2.) It is difficult to see
precisely where the period-two points are located after the bifurcation without a
careful cobweb plot. However, if we graph the second iterate f
2
a
, as in Figure 11.4,
the period-two orbit of f
a
appears as two fixed points. We can also see from slopes
on the graph of f
2
a
that the bifurcating fixed points are attractors.
✎ E XERCISE T11.1
Notice in Figure 11.4(b) that the period-doubling bifurcation point is an
inflection point for f
2
a
.Does(f
2
a
)
have to equal 0 at a period-doubling
bifurcation point?
-2
-1
0
1
2
-2 -1 0 1 2
-2
-1
0
1
2
-2 -1 0 1 2
-2
-1
0
1
2
-2 -1 0 1 2
(a) (b) (c)
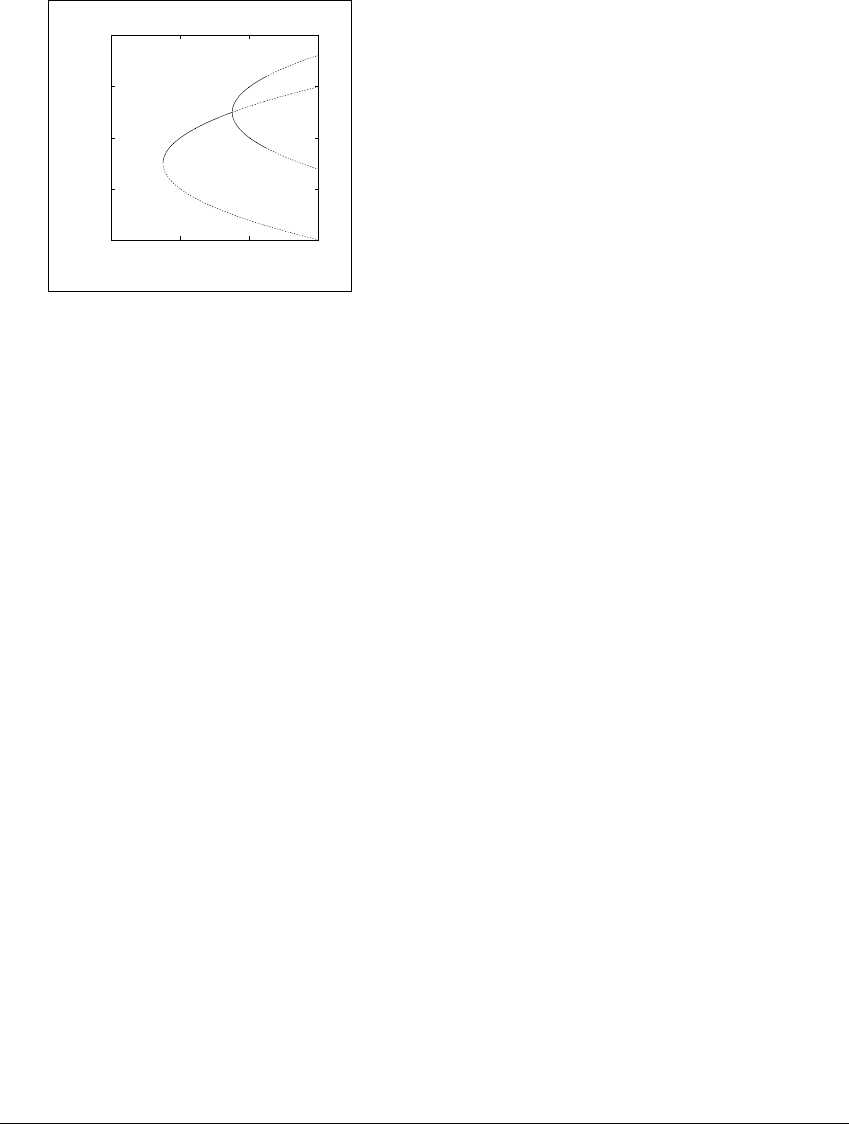
Figure 11.4 The second iterate of the quadratic map at a period-doubling
bifurcation.
(a) The second iterate f
2
a
of the quadratic map f
a
(x) ⫽ a ⫺ x
2
is graphed at a ⫽ 0.5,
before the bifurcation. The fixed point above zero is an attractor. (b) The function
f
2
a
is graphed at a ⫽ .75, the bifurcation parameter. The line y ⫽ x is tangent to the
graph at the positive fixed point, which is an attractor (although not a hyperbolic
one). (c) At a ⫽ 1, following the bifurcation, there are three nonnegative fixed
points of f
2
a
: a flip repeller fixed point of f
a
surrounded by a period-two attractor of f
a
.
452
11.2 BIFURCATION D IAGRAMS
-2
-1
0
1
2
-1 0 1 2
x
a
o
o
o
o
(-1/4,-1/2)
(3/4,1/2)
Figure 11.5 Diagram of a period-doubling bifurcation.
Fixed points and period-two orbits of the quadratic family f(a, x) ⫽ a ⫺ x
2
are
shown. Attractors are on solid curves, while repellers are on dashed curves. The
circles denote the location of the bifurcation orbits.
Figure 11.5 is a bifurcation diagram showing the fixed points and period-two
points of f as a function of a and x near the period-doubling bifurcation point.
Again, attracting orbits are shown with solid curves and repellers are indicated
with dashed curves. At a ⫽ 5 4, the derivative of f
2
a
moves past the border at ⫺1,
causing another period-doubling bifurcation. For values of a greater than 5 4and
less than the next period-doubling value, orbits are attracted to a period 4 sink.
11.2 BIFURCATION DIAGRAMS
Periodic orbits of periods greater than one can come into (or go out of) existence
through saddle-node bifurcations, and they can undergo period-doubling bifur-
cations. Nothing new is involved—it is only a matter of applying the ideas we
have already seen to a higher iterate f
k
a
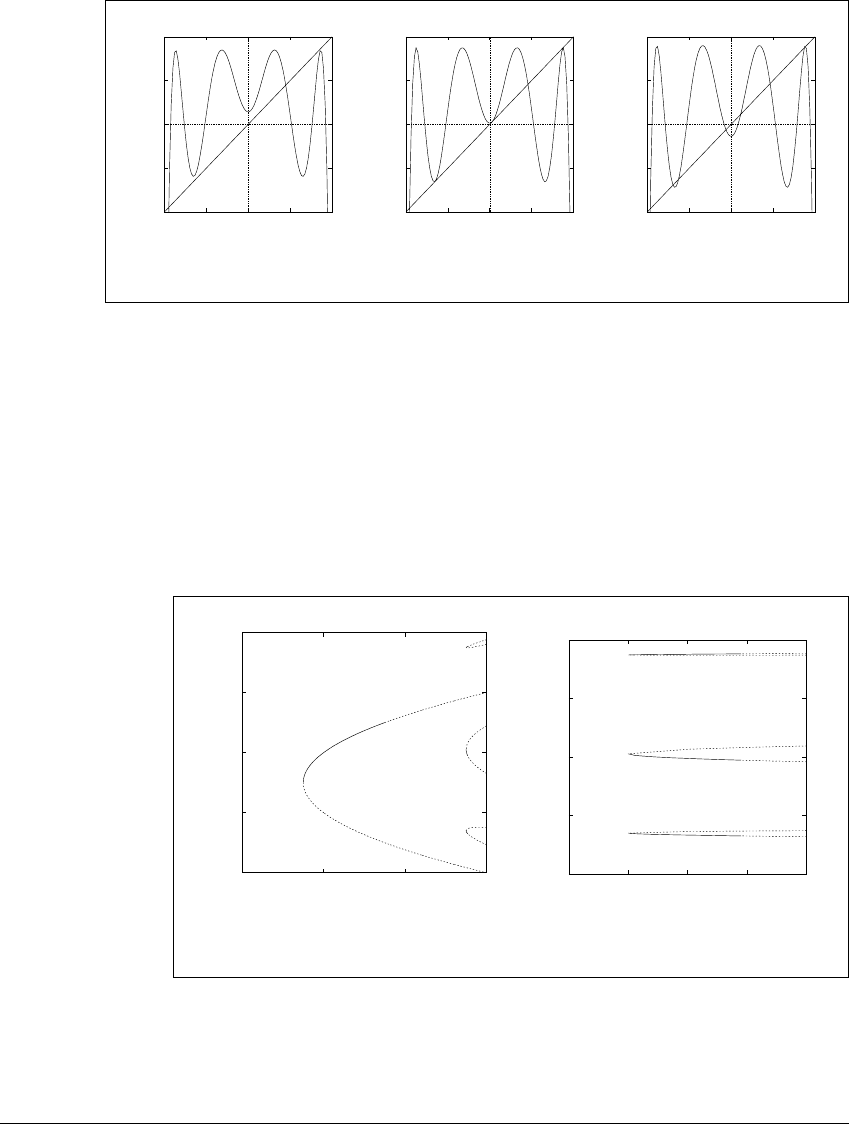
. For example, Figure 11.6 shows the graph
of f
3
a
for three values of a before, at, and following a saddle-node bifurcation at
a ⫽ 1.75. Note the simultaneous development of three new fixed points of f
3
a
at
the bifurcation value. The map f
a
is a degree-two polynomial and so can have at
most 2 fixed points; they are already shown in Figure 11.6(a). Since the three new
points are not fixed points, they must represent a new period-three orbit of f
a
.
Figure 11.7 shows the bifurcation diagram of period-three points of f near
a ⫽ 1.75. In the bifurcation diagram, two branches of fixed points of f
3
a
are shown
to emanate from each of the three points in the bifurcation orbit. On one branch,
453
B IFURCATIONS
-2
-1
0
1
2
-2 -1 0 1 2
-2
-1
0
1
2
-2 -1 0 1 2
-2
-1
0
1
2
-2 -1 0 1 2
(a) (b) (c)
Figure 11.6 A period-three saddle-node bifurcation.
Graphs of the third iterate of the quadratic map f
a
(x) ⫽ a ⫺ x
2
before, at, and
following a period-three saddle-node bifurcation. (a) At a ⫽ 1.7, there are two
solutions of f
3
a
(x) ⫽ x. (b) The bifurcation point a ⫽ 1.75. (c) At a ⫽ 1.8, there
are eight solutions of f
3
a
(x) ⫽ x.
-2
-1
0
1
2
-1 0 1 2
x
a
-2
-1
0
1
2
1.74 1.75 1.76 1.77 1.78
x
a
(a) (b)
Figure 11.7 The bifurcation diagram of a period-three saddle-node bifurca-
tion.
(a) Fixed points of f
3
are shown for the quadratic family f(a, x) ⫽ a ⫺ x
2
;(b)a
magnification of (a) near the saddle node shows only the period-three orbits.
454

11.2 BIFURCATION D IAGRAMS
the branch of stable periodic orbits, the derivative of f
3
a
decreases from ⫹1as
a increases; on the other, the branch of unstable periodic orbits, the derivative
increases from ⫹1. In Figure 11.7(a), all fixed points of f
3
a
are shown for a in
[⫺1, 2] (including fixed points of f
a
). Figure 11.7(b) shows only period-three
points in a smaller parameter range containing the saddle-node bifurcation.
In Chapter 12 we investigate the phenomena of repeated period-doublings,
called cascades, and explain why they are so prevalent. At a period-doubling
bifurcation from a period-k orbit, two branches of period-2k points emanate from
a path of period-k points. When the branches split off, the period-k points change
stability (going from attractor to repeller, or vice versa). This change is detected
in the derivative of f
k
which, when calculated along the path of fixed points,
crosses ⫺1.
For maps of dimension greater than 1 (maps whose state space is at least
two-dimensional), a bifurcation that creates period-k points can only occur when
an eigenvalue of the Jacobian Df
k
passes through ⫹1. Again, the letter D here
means we are taking partial derivatives with respect to the coordinates x and y,
not a. Figure 11.8(a) depicts a saddle-node bifurcation in a parametrized map of
the plane. A period-doubling bifurcation is illustrated in Figure 11.8(b). As in the
one-dimensional case, these two bifurcations are the ones most typically seen. The
following example illustrates the saddle-node and period-doubling bifurcations
for a H
´
enon family of two-dimensional maps.
a
0
a
a
0
a
(a) (b)
Figure 11.8 Bifurcations in a parametrized map of the plane.
(a) A fixed point appears at parameter a ⫽ a
0
in a saddle-node bifurcation. For a ⬎ a
0
there is an attracting fixed point and a saddle fixed point. The cross-sectional figures
depict the action of the planar map at that parameter value. (b) An attracting fixed
point loses stability at a ⫽ a
0
in a period-doubling bifurcation. For a ⬎ a
0
there is a
saddle fixed point and a period-two attractor.
455

B IFURCATIONS
E XAMPLE 11.3
(H
´
enon map.) Let h
a
(x, y) ⫽ (a ⫺ x
2
⫹ by, x), for fixed b, with |b| ⬍ 1.
In principle, we might also consider b as a parameter, but our purpose here
is to describe bifurcations of one-parameter families. See Example 11.14 for a
discussion of the phenomena that can occur for fixed a and varying b. The map
h has fixed points when the equations a ⫺ x
2
⫹ by ⫽ x and y ⫽ x are satisfied;
when a ⫺ x
2
⫹ bx ⫽ x. Fixed points occur at
p
a
⫽
⫺(1 ⫺ b) ⫹
(1 ⫺ b)
2
⫹ 4a
2
,
⫺(1 ⫺ b) ⫹
(1 ⫺ b)
2
⫹ 4a
2
and
q
a
⫽
⫺(1 ⫺ b) ⫺
(1 ⫺ b)
2
⫹ 4a
2
,
⫺(1 ⫺ b) ⫺
(1 ⫺ b)
2
⫹ 4a
2
,
when these expressions are defined. In particular, for a ⬍⫺
1
4
(1 ⫺ b)
2
, there
are no fixed points; for a ⬎⫺
1
4
(1 ⫺ b)
2
, there are two fixed points; and at
a
⫹
⫽⫺
1
4
(1 ⫺ b)
2
there is a saddle-node bifurcation. At a
⫹
, the fixed point is
p
a
⫹
⫽ q
a
⫹
⫽ (⫺(1 ⫺ b) 2, ⫺(1 ⫺ b) 2). Verify that the Jacobian Dh(p
a
⫹
)has
an eigenvalue of ⫹1.
For a greater than (but near) a
⫹
, the fixed point p
a
is an attractor, and
the fixed point q
a
is a saddle. Then at a
⫺
⫽
3
4
(1 ⫺ b)
2
there is a period-doubling
bifurcation from the branch p
a
of attractors. At a
⫺
, the fixed point from which
the bifurcation occurs is p
a
⫺
⫽ ((1 ⫺ b) 2, (1 ⫺ b) 2). Verify that the Jacobian
Dh(p
a
⫺
) has an eigenvalue of ⫺1.
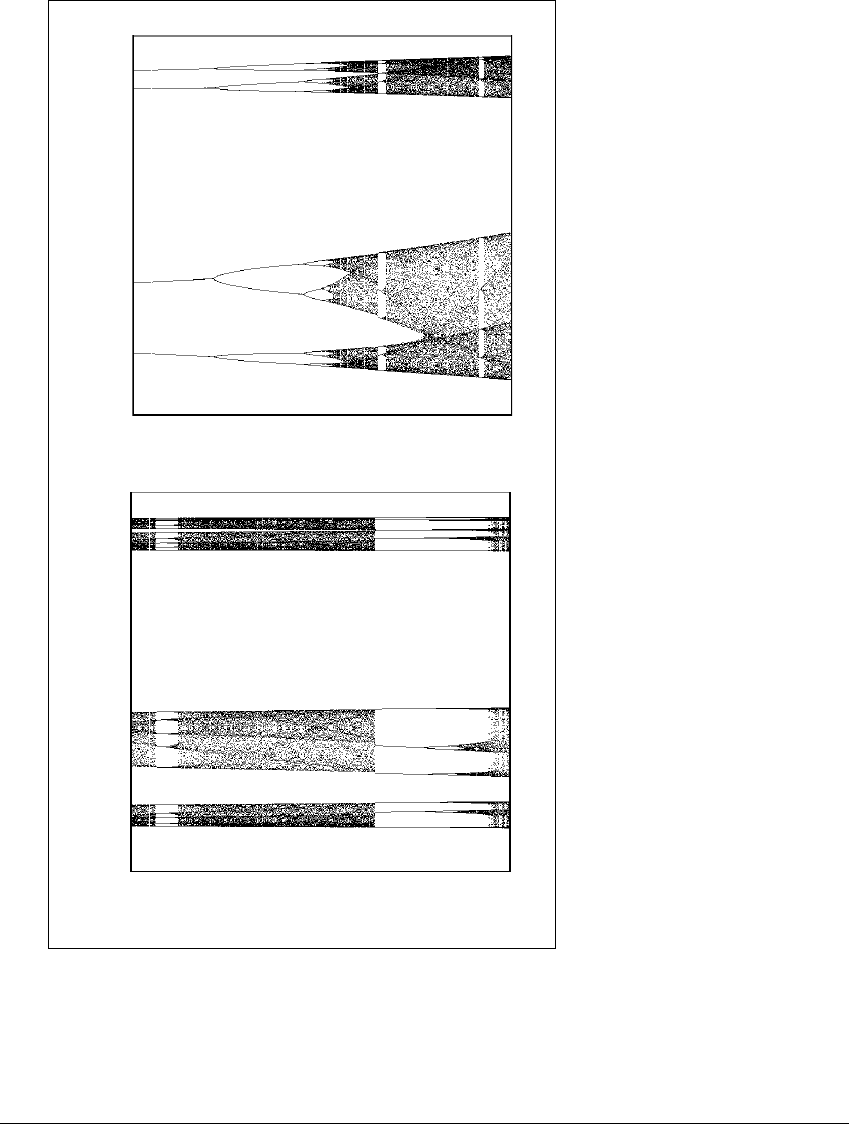
Figure 11.9(a) shows the bifurcation diagram (projected onto the x-axis) for
b ⫽⫺0.3anda in the range [1. 9, 2]. A magnified version of the range [1.96, 1.97]
is shown in Figure 11.9(b). Notice that the same type of cascade behavior observed
in the one-dimensional quadratic map is hinted at in these figures.
E XAMPLE 11.4
(Logistic map.) Define g
a
(x) ⫽ ax(1 ⫺ x). As a increases from 0 to 4, the
maximum of g (occuring at x ⫽ 1 2) increases from 0 to 1. As it does, the parabola
stretches but still has a fixed point at x ⫽ 0. Since the equation
ax(1 ⫺ x) ⫽ x (11.1)
has real root(s) for all a (one of them is x ⫽ 0),g
a
has fixed points for all a.
456
11.2 BIFURCATION D IAGRAMS
1.7
⫺0.7
1.9 2.0
(a)
1.7
⫺0.7
1.96 1.97
(b)
Figure 11.9 Bifurcation diagrams for the H
´
enon map.
The x-coordinate is plotted vertically, and the horizontal axis is the bifurcation
parameter a for the family h
a
(x, y) ⫽ (a ⫺ x
2
⫺ 0.3y, x). (a) A period-four orbit
at a ⫽ 1.9 period-doubles to chaos. At a ⫽ 2 the attractor is a two-piece chaotic
attractor. (b) A magnification of the period-twelve window in (a).
457

B IFURCATIONS
-0.5
0
0.5
1
0 1 2 3 4
x
a
Figure 11.10 Transcritical bifurcation of fixed points in the logistic family.
The bifurcation shown here is atypical in that it is neither a saddle-node nor a period-
doubling bifurcation. This type of bifurcation occurs since the graph is constrained
to pivot about the fixed point (0, 0) as the parameter changes.
Equation (11.1) has exactly two roots, except at a ⫽ 1, when x ⫽ 0isa
double root. The two paths of fixed points for a ⬍ 1 move toward one another
and cross at a ⫽ 1. At this point, the fixed point 0 loses stability and the other
fixed point becomes an attractor. Figure 11.10 shows the bifurcation diagram for
fixed points of this map. The term transcritical is sometimes used for this type
of bifurcation, when two paths meet and exchange stability. Elsewhere in the
bifurcation diagram for this family there are saddle-node bifurcations for periodic
orbits of periods greater than one, as well as period-doubling bifurcations. Both
can be seen in Figure 1.6 of Chapter 1.
✎ E XERCISE T11.2
Find a period-doubling bifurcation for the map g
a
(x) ⫽ ax(1 ⫺ x) of Example
11.4.
E XAMPLE 11.5
Let f
a
(x) ⫽ x
3
⫺ ax. Figure 11.11 shows the graph of f for values of a before,
at, and following a bifurcation of fixed points at a ⫽⫺1. The bifurcation diagram
of fixed points is shown in Figure 11.12. Notice that all maps in the family have at
least one fixed point. For each a ⱕ⫺1, there is one fixed point. For each a ⬎⫺1,
there are three fixed points.
458
11.2 BIFURCATION D IAGRAMS
-2
-1
0
1
2
-2 -1 0 1 2
y
x
-2
-1
0
1
2
-2 -1 0 1 2
y
x
-2
-1
0
1
2
-2 -1 0 1 2
y
x
(a) (b) (c)
Figure 11.11 A pitchfork bifurcation.
The graphs of the cubic maps f
a
(x) ⫽ x
3
⫺ ax before, during and after a pitchfork
bifurcation. (a) a ⫽⫺2(b)a ⫽⫺1(c)a ⫽ 0.
We will see in Section 11.4 that this bifurcation, called a pitchfork bi-
furcation, is atypical, or “nongeneric”, in the sense that it depends on special
circumstances. In this case, the special circumstance is the symmetry the map has
across the origin, since f
a
is an odd function: f
a
(⫺x) ⫽⫺f
a
(x). This symmetry
implies (1) that x ⫽ 0 is a fixed point (since f
a
(0) ⫽⫺f
a
(0)) and (2) that if x is
a fixed point, then so is ⫺x.
-2
-1
0
1
2
-2 -1 0 1 2
x
a
Figure 11.12 The bifurcation diagram for a pitchfork bifurcation.
Fixed points of the family of cubic maps f
a
(x) ⫽ x
3
⫺ ax are shown. This type of
bifurcation is not unusual for the special class of maps which are odd functions, for
which f
a
(x) ⫽⫺f
a
(⫺x).
459
