Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems

Подождите немного. Документ загружается.

C ASCADES

different types of branches. We may therefore refer to branches as stable (or S)

branches, regular unstable (or U

⫹

) branches, etc.

Deﬁnition 12.6 A cascade from period k is a connected set of branches

and bifurcation orbits containing stable branches of period k, 2k, 4k,...,all lying

in a bounded region of parameter and phase space. The connected set will also

contain unstable orbits.

Since we are interested in how chaotic sets develop, we assume Hypotheses

12.7 hold for some closed, bounded region V of phase space. For one-dimensional

maps, V is an interval [x

], while for two-dimensional maps, V could be chosen

to be a disk. We discuss only orbits all of whose points lie in V.

Hypotheses 12.7 Hypotheses for the Cascade Theorem.

1. There is a parameter value a ⫽ a

for which f has only stable ﬁxed points

or stable periodic points. In particular, it may have no periodic points.

2. There is a parameter value a ⫽ a

⬎ a

(c for “chaotic”) for which f

has unstable periodic points and for which the only periodic orbits are

in U

⫹

or U

⫺

. (Of course, in some cases the order of a

and a

will be

reversed, but we choose one case to make the discussion simpler.)

3. For a between a

and a

, the periodic orbits of f all lie in a bounded

region V of phase space. A weaker statement may also be used: there are

no periodic orbits of f on the boundary of the set V.

4. The map f satisﬁes the Generic Bifurcation Hypotheses of Deﬁnition

12.3. In particular, all bifurcations look like those shown in Figures 12.7

and 12.10, and, for each k, there are only ﬁnitely many bifurcation orbits

in [a

] ⫻ V.

In Theorem 12.8, we refer to a connected set of orbits. Thinking of a

period-k orbit as a collection of k periodic points, we mean the connected set of

branches together with endpoints (bifurcation orbits) to which a particular orbit

belongs. For a period-k orbit, there will be k distinct connected sets of periodic

points underlying this one connected set of orbits.

Theorem 12.8 (The Cascade Theorem.) Assume Hypotheses 12.7. Let p

be a regular unstable periodic orbit of f of period k at a ⫽ a

. Then p is contained in a

connected set of orbits that contains a cascade from period k. Distinct regular unstable

orbits at a ⫽ a

yield distinct cascades: If p

and p

are two regular unstable orbits at

a ⫽ a

, then the two cascades associated with p

and p

have no branches of stable orbits

in common.

520

12.4 THE C ASCADE T HEOREM

Before going into the proof of Theorem 12.8, we focus again on the type

of situation to which the theorem applies: namely, a one-parameter family of

maps for which at an initial value of the parameter there are no ﬁxed points or

periodic points or only sinks, and at a later parameter value there are only unstable

ﬁxed points or periodic points, such as in a chaotic set. We were introduced to

cascades in the bifurcation diagram of the logistic map (see, for example, Figure

6.3 of Chapter 6). The one-dimensional quadratic family f

(x) ⫽ a ⫺ x

satisﬁes

Hypotheses 12.7 for (a, x)in[⫺2, 2] ⫻ [⫺2, 2]. (See Exercise 12.1.) Our primary

two-dimensional example is the formation of a horseshoe in a family of area-

contracting maps. For example, (Devaney and Nitecki,1979) proved that for

ﬁxed b, ⫺1 ⬍ b ⬍ 0, the H

enon family H(x, y) ⫽ (a ⫺ x

⫹ by, x) develops a

horseshoe as the parameter a is varied. In particular, for a ⬍

⫺(1⫺b)

, H has no

ﬁxed or periodic points, and for a ⬎

(5 ⫹ 2



5)(1 ⫺ b)

, a hyperbolic horseshoe

exists. All periodic points and ﬁxed points in this family are contained within a

bounded region of the plane.

The proof of Theorem 12.8 follows from a few key ideas that we split off

as lemmas for you to verify. First we isolate a path of orbits in (a, x)-space within

the possibly vast and interconnected network of orbits that can occur even in

the generic case. The path will enable us to follow cascades even when there are

numerous saddle nodes, period doublings, and period halvings along the path.

Deﬁnition 12.9 For any point (a, x) on a periodic orbit that is not a ﬂip

unstable orbit, deﬁne the snake through (a, x) to be the collection of S branches

and U

⫹

branches and their endpoints (bifurcation orbits) that can be reached by

a connected path of these branches and their endpoints from (a, x). See Figure

12.12.

✎ E XERCISE T12.6

Verify that a snake passes through an orbit in S, U

⫹

, or a bifurcation orbit

as a one-dimensional path of orbits.

Notice that a snake can be a closed loop of orbits. If it is not, however, then

the snake will never go through any orbit twice. The following lemma says that

under Hypotheses 12.7 regular unstable orbits cannot period double.

Lemma 12.10 When a period-k branch in a snake ends in a period-

doubling bifurcation orbit of period k,thenitisanS branch.

521

C ASCADES

16k

...

Figure 12.12 Snakes in a generic bifurcation diagram.

A snake is a connected path of orbits, none of which are ﬂip unstable orbits. Three

snakes are shown in this schematic diagram, which is constructed by eliminating

the ﬂip unstable branches in Figure 12.11.

Lemma 12.10 is proved by observing that it holds for the four cases in

Figure 12.10. Speciﬁcally, since the only branches on a snake are S branches and

⫹

branches, the period-k branch must be a stable branch. (The fact that there

are no generic period-doublings with U

⫹

branches of period-k follows originally

from the assumption of area-contraction: If one eigenvalue crosses ⫺1atthe

bifurcation point, the other cannot be greater than ⫹1. For one-dimensional

maps, the derivative must move through ⫺1.)

Since snakes are composed only of S and U

⫹

branches, the direction of

travel along a snake (whether a is increasing or decreasing) will change precisely

at a bifurcation orbit, when moving from an S branch to a U

⫹

branch or vice

versa. See Figure 12.12, where S branches are indicated with arrows pointed to

the right, and U

⫹

branches, with arrows pointed to the left. We may say that

a snake enters (or leaves) a region if it has one orbit on the boundary and the

522

12.4 THE C ASCADE T HEOREM

directed path enters (or leaves, according to the direction of arrows) the region

at that orbit.

Lemma 12.11 implies that once a snake enters [a

] ⫻ V, entering either

from the right at a ⫽ a

as a U

⫹

branch, or from the left at a ⫽ a

as an S branch,

the snake is trapped inside [a

] ⫻ V.

Lemma 12.11 No snakes leave [a

] ⫻ V.

✎ E XERCISE T12.7

Prove Lemma 12.11.

Lemmas 12.12, 12.13, and 12.14 together establish that a snake must con-

tain inﬁnitely many bifurcation orbits, only ﬁnitely many of which can be of a

given period N or less. Therefore, the snake must contain bifurcation orbits of

arbitrarily large periods. Since, for a generic family, the only way periods can

increase along a snake is for it to contain period doublings, we obtain the desired

cascade.

Lemma 12.12 Any snake that is not a closed loop of orbits must contain

inﬁnitely many branches and inﬁnitely many bifurcation orbits.

✎ E XERCISE T12.8

Prove Lemma 12.12.

Lemma 12.13 follows from the generic bifurcation hypotheses.

Lemma 12.13 Let N ⬎ 0 be given. A snake contains only ﬁnitely many

bifurcation orbits of period N or less for parameter values between a

and a

✎ E XERCISE T12.9

Prove Lemma 12.13.

Lemma 12.14 The snake must pass through bifurcation orbits of periods

k,2k,4k,8k,...,and stable branches of periods k,2k,4k,8k,....

523

C ASCADES

✎ E XERCISE T12.10

Prove Lemma 12.14.

To summarize: Assuming that there are only stable orbits at a

and no stable

orbits at a

, we have shown that each regular unstable orbit at a

must lie on a

connected set of orbits containing a cascade. Generically, an orbit in U

⫹

is born

in a saddle-node bifurcation, paired with an orbit in S of the same period. The

stable orbit then sheds its stability through a period-doubling cascade.

Now we can translate the theorem within an appropriate system. For one-

dimensional families, the stable orbits are attractors, and the unstable orbits are

repellers, either regular or ﬂip. Higher-dimensional systems where orbits have at

most one unstable direction are also appropriate. For families of area-contracting

maps of the plane, the stable orbits are attractors, while the unstable orbits are

saddles, regular or ﬂip.

As a ﬁnal result, we restate the Theorem 12.8 within this setting.

Theorem 12.15 Let f be a family of area-contracting maps of the plane that

satisfy Hypotheses 12.7, and let p be a regular saddle of f of period k at a ⫽ a

. Then p

is contained in a connected set of orbits that contains a cascade from period k. Distinct

saddles at a ⫽ a

yield distinct cascades: If p

and p

are two saddles at a ⫽ a

, then the

two cascades associated with these saddles have no branches of attractors in common.

✎ E XERCISE T12.11

Explain which of the arguments in the proof of the Cascade Theorem

depend on the assumption that orbits have at most one unstable direction.

(This assumption underlies the structure of the generic bifurcations.)

We conclude with a brief discussion of moving from the generic to the

general case. In particular, Theorem 12.8 holds for any smooth one-parameter

family f of area-contracting maps of ⺢

for which hypotheses (1)–(3) of (12.7)

hold (see (Yorke and Alligood, 1985) for the limit arguments). Families of area-

preserving maps of the plane can also be approximated by maps in our generic

set, although in the area-preserving case, the stable orbits are not attractors but

elliptic orbits. Thus, for families of area-preserving maps of the plane that satisfy

hypotheses (1)–(3) of (12.7), period-doubling cascades of elliptic orbits will occur.

524

C HALLENGE 12

☞ C HALLENGE 12

Universality in Bifurcation Diagrams

HE STABILITY ARGUMENTS of this chapter have shown us why period-

doubling cascades must occur in certain systems that develop chaos. Not only

are distinct cascades qualitatively similar, as seen in Figure 12.2, but they also

have metric properties in common, as we saw with Feigenbaum’s discovery for

one-parameter families of one-dimensional maps.

Self-similarity within a cascade follows from the basic idea that higher

iterates of the map can be rescaled in a neighborhood of the critical point to

resemble the original map. For example, Figure 12.13 shows the graphs of iterates

of two maps in the quadratic family g

(x) ⫽ x

⫺ a. In Figure 12.13(a), g

graphed for g(x) ⫽ x

⫺ 1. At this parameter (a ⫽ 1), the origin is a period-two

point of g, (a ﬁxed point of g

). In Figure 12.13(b), g

is graphed for g(x) ⫽

⫺ 1.3107. The origin is a period-four point of g. In each case, the graph in a

-2

-1

-2 -1 0 1 2

-2

-1

-2 -1 0 1 2

(a) (b)

Figure 12.13 Iterates of maps within the quadratic family

(

) ⴝ

ⴚ

(a) The origin is a period-two point of g(x) ⫽ x

⫺ 1. The second iterate g

graphed. (b) The origin is a period-four point of g(x) ⫽ x

⫺ 1.3107. The fourth

iterate g

is graphed. In each case, a neighborhood of the origin in phase space and

of the appropriate a-value in parameter space can be rescaled so that the dynamic

behavior of the iterate in the small scale mimics that of the whole quadratic family

in the large.

525

C ASCADES

neighborhood of the critical point can be rescaled to look like the graph of x

⫺ a

at a ⫽ 0. For example, the map g

in Figure 12.13(a) would be ﬂipped about the

horizontal axis and rescaled. As a is increased, each parabolic region mimics the

behavior of x

⫺ a. Thus sequences of bifurcations, such as cascades, could be

expected to be the same for g

in a neighborhood of x ⫽ 0anda ⫽ 1 and for g

in a (still smaller) neighborhood of x ⫽ 0anda ⫽ 1.3107 as for g

(x) ⫽ x

⫺ a.

In Challenge 12 we examine universal metric properties among different

windows of periodic behavior within chaotic regions of parameter space. The

arguments are given for one-parameter families of scalar unimodal maps, although

the phenomena seems to occur within families of area-contracting planar maps as

well. We show that, typically, the distances between bifurcations (both local and

global) within a periodic window are well-approximated by the corresponding

distances for the canonical map g

(x) ⫽ x

⫺ a under a suitable linear change of

coordinates. The procedure of rescaling to obtain universal properties is known

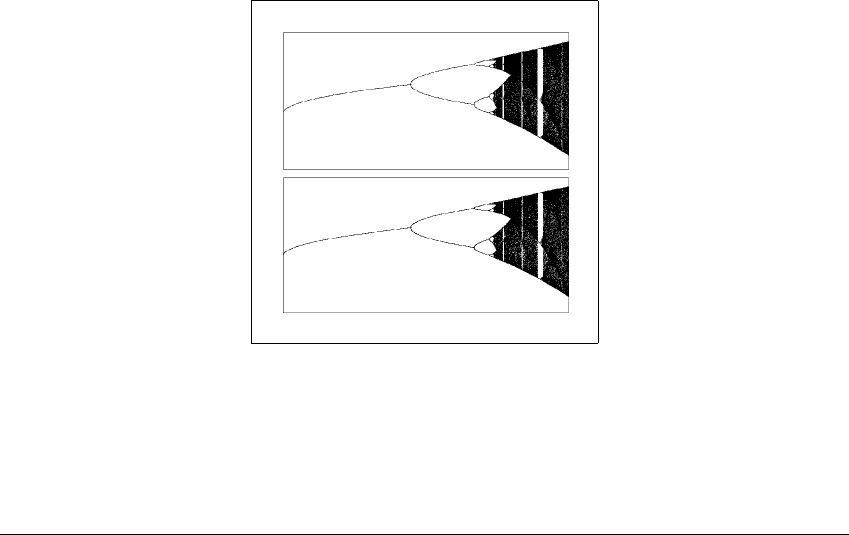
as renormalization. Figure 12.14 shows ﬁrst the complete bifurcation diagram for

the map g

(x) followed by a period-nine window for g

. The relative distances

between corresponding bifurcations are strikingly similar.

A period-n window begins with a period-n saddle node at a ⫽ a

. The stable

period-n orbit then loses stability through a period-doubling cascade, eventually

forming an n-piece chaotic attractor. The window ends at the crisis parameter

Figure 12.14 Universality in periodic windows.

The complete bifurcation diagram for the map g

(x) ⫽ x

⫺ a is shown above,

while the bifurcations for g

within a period-nine window are shown below. In the

top diagram, x goes from ⫺2.0to2.0anda is between ⫺0.25 and 2.0, while in

the bottom diagram x goes from ⫺0.02 to 0.02 and a is between 1.5552567 and

1.5554906.

526

C HALLENGE 12

value a ⫽ a

at which the n-piece attractor disappears. As with a planar map,

this crisis occurs when the attractor collides with a basin boundary orbit—in this

case, with a period-n source. (See Chapter 10 for a discussion of the planar case.)

The basin of the chaotic attractor includes the union of n disjoint open intervals,

each of which contains a piece of the attractor and one of which contains the

critical point of the map. Since the critical point must map to an endpoint of one

of these intervals, the crisis occurs precisely when the critical point maps onto

one of the period-n boundary sources.

Within a window, we denote the ﬁrst period-doubling bifurcation parameter

by a ⫽ a

. Between the saddle-node at a

and the period-doubling at a

, the path

of stable period-n orbits must pass through a parameter where the orbit has

derivative 0. At this parameter, denoted a ⫽ a

, the orbit is called superstable

and contains a critical point x

of the map.

Step 1 Show that the ratio R

⫽ (a

⫺ a

) (a

⫺ a

)is

for the period-

one window of the canonical family g

(x) ⫽ x

⫺ a. [Hint: Find an interval that

maps onto itself to determine a

Let k

be a family of scalar maps that is linearly conjugate to the canonical

family of maps g

. Speciﬁcally, deﬁne G : ⺢

→ ⺢

to be (a, x) → (a, g

(x)) and

K : ⺢

→ ⺢

to be (a, x) → (a, k

(x)). Then G and K are said to be linearly

conjugate if there is a linear map H : ⺢

→ ⺢

such that H ◦ K ⫽ G ◦ H. The

form of the linear map we use here is H(a, x) ⫽ (C

(a ⫺ a

),C

(x ⫺ x

)), for

nonzero constants C

Step 2 Show that k has a period-n saddle node or period-doubling bi-

furcation at (a, x) or a crisis at a

if and only if g has a period-n saddle node or

period-doubling bifurcation at (C

(a ⫺ a

),C

(x ⫺ x

)) or a crisis at C

⫺ a

respectively.

Conclude for the map k that R

⫽ (a

⫺ a

) (a

⫺ a

)is

. Furthermore, any

ratio of distances deﬁned by conditions on periodic points and their derivatives

is preserved under a linear conjugacy.

Now we focus on an arbitrary family f of unimodal maps that has a super-

stable period-n orbit, 兵x

,...,x

n⫺1

其,ata ⫽ a

. Again, let F(a, x) ⫽ (a, f(a, x)).

We assume that x

is the critical point and show that, under certain assumptions,

there is a neighborhood of (a

) and a linear change of coordinates H for which

⫺1

is approximated by the canonical family G. The larger n, the period of

the orbit, the closer the approximation, with the distance between them (and

their partial derivatives up to a given order) going to 0 as n goes to inﬁnity. The

527

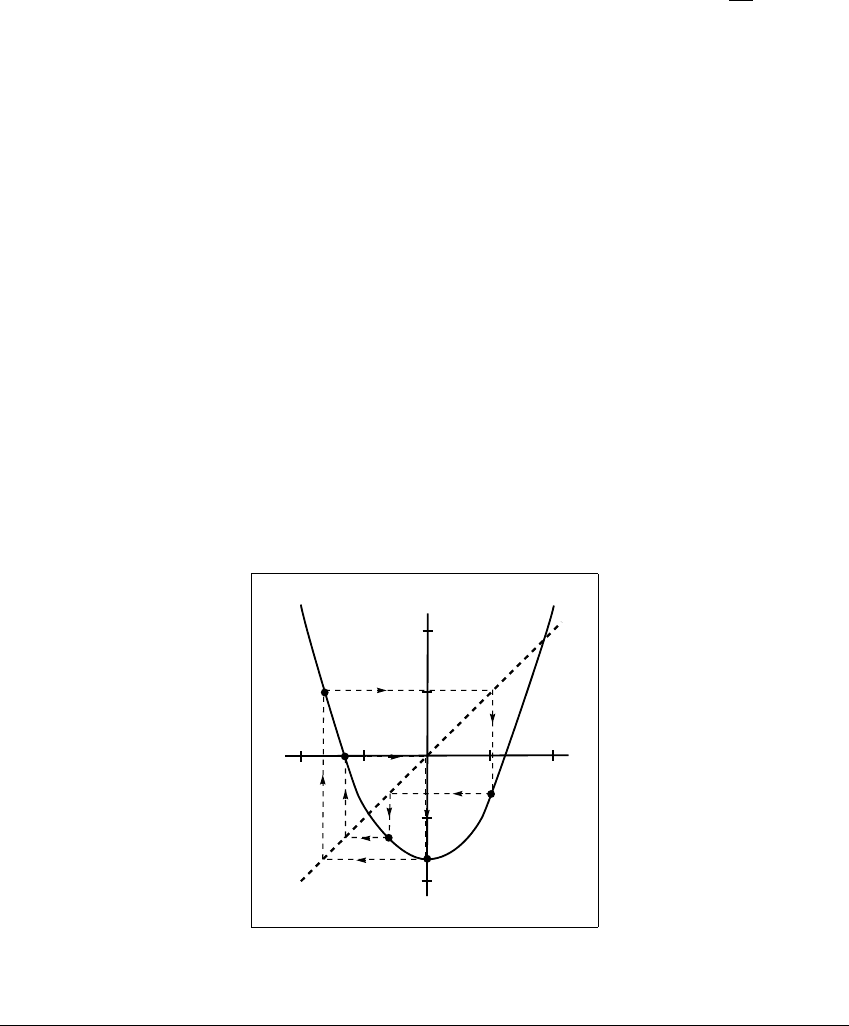
C ASCADES

ratio R

in periodic windows for which the hypotheses are well-satisﬁed is re-

markably close to R

⫽ 9 4. We illustrate this correspondence at the end of this

challenge with one of several published numerical studies of the phenomenon.

We say a function k(n)isoforder g, denoted

O(g), if lim

n→

⬁

k(n)

g(n)

is bounded.

For example, n

is O(2

), but 2

is not O(n

When the orbit of x

is superstable, the map f will typically be quadratic near

, the critical point, and a neighborhood of x

will be folded over by f and then

stretched by the next n ⫺ 1 iterates of f before returning close to x

. See Figure

12.15. In order to get an intuitive idea of what is happening here, we describe an

idealized f

: there is a cycle of n disjoint intervals J

,...,J

n⫺1

that the map f

permutes so that f is quadratic on J

and linear on the remaining J

’s. Speciﬁcally,

(a, x) ⫽ L

n⫺1

⭈⭈⭈L

Q(a, x), for constants L

,...,L

n⫺1

which, in the ideal

case, do not depend on a, for a quadratic map Q, which depends on both x and a,

and for x 僆 J

and a 僆 [a

⫺ a

]. Notice that under this simplifying assumption

: J

→ J

is quadratic. Ideally, the parameter extent of the window, a

⫺ a

is sufﬁciently small that the n ⫺ 1 points in the orbit remain far away from the

critical point and that the constants L

,...,L

n⫺1

remain good approximations

to the slopes of f

near these points throughout the parameter window.

Let S ⫽

⳵

n⫺1



⳵

x(a

). (For our idealized map, S is the product of slopes

⭈⭈⭈L

n⫺1

.) We make the following speciﬁc assumptions incorporating the ideas

in the previous paragraph:

2- 2

- 2

Figure 12.15 A superstable period-5 orbit.

The map is f(x) ⫽ x

⫺ 1.6254.

528

C HALLENGE 12

(1) S grows exponentially with n; that is, there is a constant r, r ⬎ 1, such

that S is

O(r

). (This assumption holds if the remaining points in the

orbit, 兵x

,...,x

n⫺1

其, are “far” from the critical point. How far, will

determine in part how well the renormalization procedure succeeds in

approximating the canonical map.)

(2) The second partial

⳵



⳵

is nonzero at (a

(3) The partial

⳵



⳵

a(a

) is nonzero.

By rescaling both x and a near (a

), we can make the lowest order terms

in the Taylor series for f

match those of the canonical map. The hard part then

is to show that the higher-order terms are made small by the rescaling. We give

a heuristic argument here, based on estimating the order of the error term in

a Taylor expansion of f

. More technical estimates including bounds on higher

order partial derivatives can be found in (Hunt, Gallas, Grebogi, and Yorke, 1995).

Step 3 Typically, all the kth order partial derivatives of f

n⫺1

taken with

respect to a and x near (a

) are of order S

. We illustrate this technical point

with an example:

Show that

⳵

n⫺1



⳵

)isoforderS

. [Hint:

⳵

n⫺1

⳵

) ⫽

⳵

n⫺1

)

⳵

n⫺3

) ...

⳵

Use the product rule (together with the chain rule) to obtain the second partial

derivative.]

Step 4 Using Taylor’s Theorem, verify:

(i) There is a nonzero constant p

such that

n⫺1

(a, x) ⫺ x

⫽ S(x ⫺ x

) ⫹ p

S(a ⫺ a

)

⫹

O(S

(|x ⫺ x

⫹ |a ⫺ a

)),

provided |x ⫺ x

| and |a ⫺ a

| are small compared with S

⫺1

(ii) There are nonzero constants q and p

such that

f(a, x) ⫺ x

⫽ q(x ⫺ x

)

⫹ p

(a ⫺ a

)

⫹

O(|x ⫺ x

⫹ |x ⫺ x

||a ⫺ a

| ⫹ |a ⫺ a

for (a, x) near (a

). Recall that x

is f(a

Step 5 Compose (i) and (ii) of Step 4 to obtain

(iii) f

(a, x) ⫺ x

⫽ qS(x ⫺ x

)

⫹ pS(a ⫺ a

)

⫹

O(S

(|x ⫺ x

⫹ |a ⫺ a

))

⫹

O(S(|x ⫺ x

⫹ |x ⫺ x

||a ⫺ a

|)), (12.2)

529