Amano R.S., Sunden B. (Eds.) Computational Fluid Dynamics and Heat Transfer: Emerging Topics

Подождите немного. Документ загружается.

Sunden CH006.tex 10/9/2010 15: 39 Page 246

246 Computational Fluid Dynamics and Heat Transfer

on these criteria, out of all the schemes the TVD limiter is the most dissipative

even when used with the nondissipative SOC scheme. The QUICK scheme is not

as dissipative as the TVD limiter, but in spite of having a higher accuracy than

the SOC scheme it fails to give accurate results. On the other hand, the universal

limiter behaves very much like the dynamic Smagorinsky model [29] (DSM) and

seems to be a viable alternative for turbulent ﬂow simulations.The use of minimal

numerical dissipation as in the SOC-UL method to substitute for explicit subgrid

modeling as a means for performing LES is referred to as implicit LES or ILES in

the literature (Margolin et al. [30]; Grinstein et al. [31]).

In summary, discrete approximations used for the nonlinear convection terms

have a large bearing on the accurate prediction of turbulence in time-dependent

methods based on DNS, LES, and DES.The SOC method used in its conservative

formisagoodcompromiseforcomplexgeometriesbetweenoverlydissipativelow-

order (second- and third-order upwind scheme) and the extra cost and complexity

of high-order methods.

6.7 Large-Eddy Simulations and Subgrid Modeling

Central to the large-eddy simulation of turbulence is the ﬁltering operation and

modeling of the resulting subgrid stresses. In generic terms the ﬁltering operation

is deﬁned by a low-pass 3-D ﬁlter in physical space:

f (x

,t) =

+∞

−∞

i=1

− x



)f (x



,t)dx



(58)

In any discrete simulation bydeﬁnitionthere is an implicit ﬁlter inherentlyapplied

to the calculation. In physical space with ﬁnite-difference/ﬁnite-element methods

the implicit ﬁlter is referred to as the top hat ﬁlter because of its shape and is

given by:

− x



) =

x

; |x

− x



|≤x

= 0; otherwise

(59)

where

x

is the grid spacing. Similarly in spectral simulations the ﬁlter width in

wavenumber space is implicitly decided by the number of fourier modes used in

the calculation and is referred to as a shar p cut-off ﬁlter and is given by:

) = 1; k

≤ k

= 0;

otherwise

(60)

where k

is the cut-off wavenumber. In contrast, the top hat ﬁlter is not sharp in

wavenumber space but smooth suchthatit partiallyﬁlters even the high wavenum-

bers resolved on the grid (Sagaut and Meneveau [32]). Another smooth ﬁlter that

hasfound someuse forexplicit ﬁlteringis theGaussian ﬁlter.There hasbeen much

debate and research on the properties of these ﬁlters and whether explicit ﬁltering

Sunden CH006.tex 10/9/2010 15: 39 Page 247

Time-accurate techniques for turbulent heat transfer analysis 247

with a ﬁlter width larger than that of the implicit grid spacing should be used in

ﬁnite-difference/ﬁnite-volumemethods.Since ﬁnite-difference methodsinevitably

result in some corruption of the high wavenumbers of the resolved ﬁeld which are

also used to model the subgrid stresses particularly in models that assume a simi-

larity between thehigh wavenumberresolved ﬁeldand the subgrid ﬁeld, numerical

inaccuracies and modeling errors become inextricably linked together. Hence the

argument for explicit ﬁltering is to break this link by using a twice as ﬁne grid and

then explicitly ﬁltering outthe numericallycorrupted scales and usingonly the 2

ﬁltered scales to model the subgrid stresses. However, the cost of the simulation

morethandoubles(in1-D) andstudieshaveshownthatcalculationsonthe twiceas

ﬁnegridwithoutexplicit2 ﬁlteringgivebetter predictionsofturbulentquantities.

In the past, efforts on subgrid modeling focused on calculating the Leonard

terms and on modeling the individual terms in equation (21) (Leonard [33]; Clark

et al. [34]). However this effort was largely abandoned in favor of modeling all

the subgrid terms together. There are a number of subgrid-scale models varying

in complexity from eddy viscosity to one equation models. Reviews can be found

in Rogallo and Moin [35], Ferziger [36], Lesieur and Metais [37], and in the text

by Saugat and Meneveau [32]. The most widely used closure model, suggested

by Smagorinsky [38], is based on the eddy-viscosity approximation in which the

subgrid-scalestressesarerelatedtothestrainratetensoroftheresolvedﬁeldthrough

aneddyviscosity(equation(22)).Theeddyviscosityiscomputedfromtheresolved

strain rate magnitude and a characteristic length scale (equation 61). The length

scale is assumed to be proportional to the ﬁlter width via a Smagorinsky constant,

which has assumed values anywhere from C

=0.06 to 0.23 in past studies.

= C

(

√

2/3

|S| (61)

yielding

=−2C

(

√

2/3

|S|S

=−2Cβ

(62)

where C =C

, |S|=



is the magnitude of the strain rate tensor that pro-

vides the nondimensional time scale of subgrid turbulence. Germano et al. [29]

proposed a dynamic procedure for the computation of the Smagorinsky constant.

The dynamic procedure utilizes information from the resolved high wavenumber

scales by applying a test ﬁlter in addition to the grid ﬁlter to obtain the model

constant.

Central to thedynamic procedure is the applicationof a test ﬁlter denotedby

tothe ﬁlteredgoverning equations(10)and(11)with thecharacteristiclengthscale

G being larger than that of the grid ﬁlter,

G (usually

 =2). In computational

coordinates the ﬁlter is written as:

G(ξ

− ξ



) =

2ξ

; |ξ

− ξ



|≤ξ

= 0; otherwise

; i = 1,2,3 (63)

Sunden CH006.tex 10/9/2010 15: 39 Page 248

248 Computational Fluid Dynamics and Heat Transfer

and the ﬁltered quantity as:

f (ξ

) =

+ξ

−ξ

i=1

2ξ

f (ξ



)dξ



(64)

Using Simpson’s rule for a 1-D integration (say; i =2orη-direction)

f (η) =

(

j−1

+ 2f

+ f

j+1

) (65)

Using a ﬁve-point integration rule

f (η) =



(

j−1

+ 4f

j−1/2

+ 2f

+ 4f

j−1/2

+ f

j+1

)



(66)

Using a second-order interpolation at the cell faces in equation (66) leads to the

trapezoidal top hat test ﬁlter

f (η) =

(

j+1

+ 2f

+ f

j−1

) (67)

From the development above it is straightforward to extend the ﬁltering operation

to nonunifor m grids and to inhomogeneous boundaries. For example, at a wall

boundary a simple extension of the method above will give:

(η) =

+ f

) (68)

where 1 denotes the boundary node and node 2 is at

/2 from the boundary. The

one-sided ﬁlternowhas a complextransfer function and introducesphase errors in

the ﬁltering operation. Najjar and Tafti [39] studied the effect of inhomogeneous

ﬁltering in turbulent channel ﬂow and found that the local modiﬁcation to the test

ﬁlterhad aneffectonthedistributionof thedynamic constantandsubsequentlythe

turbulent viscosity at the ﬁrst few nodes near the boundary.

Usingthesamemethodologyanumberof“high-order”ﬁlterscanbeconstructed

(Najjar andTafti [40]). The high-order ﬁlters ﬁlter out a smaller percentage of the

high wavenumber resolved scales and approach the behavior of a cut-off ﬁlter. It

was determined by Najjar and Tafti [41], that the trapezoidal ﬁlter yielded more

consistent results with ﬁnite-difference approximations.

Since the grid ﬁlter is applied to the conservation equations in physical space,

for consistency the test ﬁltering operations are transformed from computational to

Sunden CH006.tex 10/9/2010 15: 39 Page 249

Time-accurate techniques for turbulent heat transfer analysis 249

physical space.This is accomplished by the following transformations:

x



f (ξ) +x

f (η) +x

f (ζ)



(69)

y



(ξ) + y

(η) + y

(ζ)



(70)

xyz

z



(ξ) + z

(η) + z

(ζ)



(71)

to give the ﬁltered variable in physical space. Contrary to the formulation of the

subgridtermsandconsequenttestﬁlteringinphysicalspace,Jordan[42]formulated

the subgrid stresses in computational space, i.e., the grid ﬁltering operation is

applied to the transformed equations.

The test ﬁltered subtest scales that include part of the grid-resolved scales and

the subgrid scales T

−

are modeled as:

=−2C

(σ

(

√

2/3

=−2Cα

(72)

whereσ is theratioofthe testﬁlterwidthtothegrid ﬁlterwidth.Themostcommon

value used in the literature is 2, which is consistent with a sharp cut-off ﬁlter. For

the trapezoidal ﬁlter, Najjar andTafti [41] obtained a value of

√

The resolved turbulent stresses representing the energy scales between the test

andthegridﬁlters,L

,arethencalculatedandrelatedtothesubtest(T

)andsubgrid

(τ

) stresses through the identity

= T

−ˆτ

, where L

−

(73)

to give

= L

−

=−2Cα

+ 2

;

Cβ

(74)

Equation (74) corresponds to a setof ﬁve independent equationsthat cannot be

solvedexplicitlyforC,whichappearsinthetestﬁlteringoperation.Asimpliﬁcation

arises if C is assumed only to be a function of time and the direction where no

explicit test ﬁltering is applied (say the y-direction), i.e., C =C(y,t), then C can

be extracted from the ﬁltering operation resulting in

;

Cβ

. Using a least-

squareminimizationprocedure(Lilly[43])forﬂowswithatleastonehomogeneous

direction, thefollowing closedformfor thedynamic subgrid-scalemodel constant,

C, is obtained:

C(y,t) =−

L

(α

−

)

2(α

−

)(α

−

)

(75)

whererepresentsanaveragingoperationinthehomogeneousdirections.Equation

(75) has been extensively used in LES computations of various turbulent ﬂows.

Sunden CH006.tex 10/9/2010 15: 39 Page 250

250 Computational Fluid Dynamics and Heat Transfer

The averaging procedure applied in equation (75) represents a smoothing operator

todamp thelarge localﬂuctuations inC. In complex geometrieshowever, thereare

no homogeneous directions and the testﬁlter is often applied in allthree directions

and C has to be computed locally. The simplest approximation is to remove C

from the ﬁltering operation in equation (74) and then apply some smoothing to the

local values of C based on zonal averaging or application of a smoothing ﬁlter not

very different from the test ﬁlter. In addition to the smoothing, some bounds are

usually placed on C or 1/Re

. The dynamic procedure is capable of predicting

C < 0 or backscatter of energy. To permit backscatter, but to prevent negative

effective viscosities and the ensuing numerical instability, −1/Re

is limited by

1/Re.However, usageincomplexgeometrieswithﬁnite-differenceapproximations

has tended to eliminate backscatter by constraining C ≥0. Just as negative values

of 1/Re

eff

can induce numerical instabilities, so can very high positive values of C

by decreasing the effective Reynolds number of the ﬂow, which could reduce the

effectivediffusivetimescalebelowthetimestep.Henceasomewhatarbitraryupper

bound on C of the order 0.04 or C

≤0.2 is also used based on the theoretically

derived value of C

=0.18 for homogeneous turbulence. More elaborate solutions

forcalculatingC fromequation(74)canbefoundinGhosaletal.[44]andMeneveau

et al. [45].

Table 6.1 summarizes calculations done in a fully developed ribbed duct from

Tafti [46] at a nominal Re=20,000. The duct is of square cross section with a

square rib of dimension e/D

=0.1 and a rib pitch of P/e =10, where e is the

dimension of the rib and P is the streamwise pitch between ribs. Four calculations

areshownatdifferentresolutionstohighlighttheeffectofthedynamicSmagorinsky

model (DSM in Table 6.1). An SOC difference scheme is used for the convective

terms. The dynamic Smagorinsky constant is localized and is constrained to be

positive. The turbulent Prandtl number was ﬁxed at 0.5 [47]. The heat transfer

results were found to be quite insensitive to the turbulent Prandtl number and tests

on a grid of 128

showed no difference when Pr

was changed to 0.9. Two grid

sizes of 96

and 128

are investigated with and without the model. Since Nusselt

numberaugmentationratioisaveryweakfunctionofReynoldsnumberintherange

20,000to 30,000, thepredictions arecompared tothe available experiments ofRau

et al. [48] at Re=30,000. The table summarizes the prediction of reattachment

length of the separation bubble behind the rib, and Nusselt and friction coefﬁcient

augmentation.

All calculations reproduce the major ﬂow structures with ﬁdelity, namely the

eddy formed at the junction between the rib and the wall, a recirculation zone

formed on top of the rib and behind the rib with a corner eddy, and the lateral

impingement of ﬂow on the smooth side wall at the rib junction. Qualitatively, the

bulk ﬂow ﬁeld results are indistinguishable, but quantitative differences of 10 to

15% exist between the different calculations. However, there are large differences

in the predicted heat transfer and friction coefﬁcients.The degree of underpredic-

tion of heat transfer and friction varies from 20 to 30% for the 96

quasi-DNS

calculation to 15 to 20% for the 128

quasi-DNS. This is caused primarily by low

turbulence intensities. The use of LES with the dynamic model increases the level

Sunden CH006.tex 10/9/2010 15: 39 Page 251

Time-accurate techniques for turbulent heat transfer analysis 251

Table 6.1. Summary of heat transfer and friction data and percentage error with

data of Rau et al. [48]. Experimental uncertainty is ±5%

Computations Rau et al. [48],

e/D

=0.1, P/e =10 e/D

=0.1,

P/e =10

DSM 128

128

DSM

6,667 6,667 6,667 6,667 –

24,000 20,000 22,000 20,000 30,000

% Form loss 92 94 92 91 85

Reattachment 4.8 4.3 4.6 4.1 4.0–4.25

length (x

/e)

<Nu>/Nu

(Nu

=0.023·Re

0.8

·Pr

0.4

)

Rib 2.22 2.84 2.54 2.89 –

Ribbed wall 1.78 2.35 2.00 2.4 2.40

(−26%) (0%) (−17%) (0%)

Smooth sidewall 1.40 1.89 1.60 1.89 2.05

(−32%) (−7%) (−22%) (−7%)

Overall with rib 1.67 2.22 1.89 2.23 –

Overall w/o rib 1.58 2.11 1.79 2.14 2.21

(−28%) (−4.5%) (−19%) (−3.4%)

f /f

=0.046·Re

−0.2

)

Overall 6.11 8.53 7.23 8.6 9.5

(−36%) (−10%) (−24%) (−9%)

of turbulence in the ﬂow, particularly near walls, and is able to predict the heat

transfer coefﬁcient to within experimental uncertainty and friction coefﬁcient to

within 10% of experiments for both mesh resolutions. The level of turbulence

augmentation provided by the dynamic model is commensurate with the mesh res-

olution such that the turbulent energy, heat transfer coefﬁcient, and friction are

predicted at the right levels independent of the resolution.

The dynamic Smagorinsky model has been used extensively in the literature

for complex ﬂows, and in spite of some as yet unresolved issues it does a reason-

able job in calculating the eddy viscosity in complex ﬂows. Chief among them is

that it is difﬁcult to separate out numerical errors from the subgrid model. Some

new developments in subgrid modeling and LES simulations can be found in the

deﬁltering approach to reconstruct the subgrid scales (Domaradzki and Saiki [49];

Domaradzki and Loh [50]; Stolz and Adams [51]), the use of grid hierarchies for

dynamic simulations on coarse grids using information from ﬁne grids to model

Sunden CH006.tex 10/9/2010 15: 39 Page 252

252 Computational Fluid Dynamics and Heat Transfer

the subgrid stresses with large savings in computational effort (Dubois et al. [52,

53],Terracol etal.[54]),andthe variationalmultiscalemethodofHughes [55,56].

Alternate methods of simulating turbulentﬂowswithout explicit subgrid modeling

have also been proposed and used [31].

6.8 Detached Eddy Simulations or Hybrid RANS-LES

LES is an attractive alternative to DNS, but is still computationally expensive in

wall-bounded ﬂows, particularly when wall friction and heat transfer coefﬁcients

are sought from the calculation. Typically, to capture the energy-producing scales

a ﬁne grid resolution is required not only in the wall normal direction (which even

wall integration or low Reynolds number RANS models require), but also in the

wall parallel direction. In typical turbulent boundary layers the streaks and bursts,

which are primarily responsible for near-wall production of turbulence, extend

about 40 spanwise wall units and are spaced about 100 wall units apart. With LES

itisimperativethatthesestructuresareresolvedinthecalculation,whichputslarge

demands onthe near-wall resolution astheReynolds numberincreases. Hence it is

not surprising that attemptshave been madeto use wall functions withLES (Cabot

and Moin [57]; Piomelli and Balaras [58]).

TheforbiddingcomputationalexpenseofLESathighReynoldscoupledwiththe

inability of RANS models to accurately predict separation and reattachment led to

thedevelopmentofDES,ormoregenerallyahybridRANS-LESmethod,bySpalart

et al. [1].The motivation behind the formulation was to allow a RANS solution in

the near-wall region which would default to LES away from the wall. Hence, in

some sense italso acted as a wall model, whereinby using RANSvery close tothe

wall,thestrictresolutionrequirementsofLESinthewallparalleldirectioncouldbe

relaxedconsiderably.Theoriginalformulationwasintroducedwithintheframework

oftheSpalart–Almaras[59](SA)model.WhatdifferentiatedtheDESmethodfrom

previous efforts to combine URANS and LES was the fact that a single model (in

this case the SAmodel) acted both as the RANS model inthe near-wall region and

asaneddy-viscositysubgridmodelinregionsawayfromthewall.Theswitchinthe

intended use of the model occurs transparently and does not involve complicated

matching of ﬂow and turbulence quantities at the interface. In the case of the SA

model, this is incorporated bycomparing the distance to the wall (d) with the local

cell size () (which in LES is representative of the smallest resolved scale). For

d < C

des

,theSAmodelisusedintheRANSmodeandwhend ≥C

des

,C

des

 is

used as the characteristic turbulence length scale for operation in LES mode.This

idea was applied successfully to airfoils with massive unsteady separation (Shur et

al.[60]), toexternalﬂowovercylinders(Travinetal.[61]), andtoturbulentchannel

ﬂow at high Reynolds numbers (Nikitin et al. [62]) and to a number of external

ﬂows with separation [63–66]. In initiating the switch from RANS to LES, while

the formulation in the SA model related the turbulent length scale to the distance

from the wall, Strelets [67] extended the DES concept to a two equation eddy-

viscosity model (SST model) by calculating the turbulent length scale from the

Sunden CH006.tex 10/9/2010 15: 39 Page 253

Time-accurate techniques for turbulent heat transfer analysis 253

DES

1.00

0.80

0.60

0.40

0.20

0.00

Rib

Figure 6.12. Plot of the time-averaged LES and RANS region in the DES com-

putation for a 64

grid in a lateral plane. A value of 1 represents a

completeLES regionanda valueof0a completeRANSregion. Flow

is periodic or fully developed in the streamwise direction. Reynolds

number based on mean ﬂow velocity and hydraulic diameter of duct

is 20,000 [69].

model turbulent quantities.This is illustrated for the k −ω model (Wilcox [68]) in

whichthedissipationofturbulentenergy, −C

kω iswrittenask

3/2

DES

.TheDES

length scale is obtained from l

DES

=min(l

RANS

LES

), where l

RANS

√

k/(C

ω)

and l

LES

DES

max(

,

) is the turbulent length scale and the grid length

scale,respectively. Foragridscalesmallerthantheturbulentlengthscalethemodel

reverts to an LES solution.This feature facilitates the computation to be cognizant

of the eddy length scales and hence behave as RANS or LES depending on the

instantaneous local conditions, unlike in the case of SA model DES, where it is

constrained to be a wall model. Another prominent feature of the DES version of

the two equation model is that although an instantaneous discontinuity may exist

between the RANS region and the LES region, in the mean however a smooth

transition takes place from RANS to LES and vice versa. Figure 6.12 plots the

fractionof timethe modeloperates inLES modeatagivenlocation inspace. Itcan

be observedfrom Figure6.12 thattheRANS regionstransition intoLES smoothly.

In a DES SA model, the distance from the wall determines the switch from RANS

to LES, which is not as receptive to instantaneous ﬂow features.

Much like the SA model the near-wall region is always resolved in the RANS

mode, which transitions to the LES mode as the distance from the wall increases.

The ﬂow in the vicinity of the ribs is mostly resolved in LES mode all the way

to the channel center. This includes the unsteady large-scale dynamics of the

separated shear layer as shown in Figure 6.12. Though the inter-rib spacing is

predominantlyLES, ittransitions to aRANS modeat the centerof inter-ribregion.

The grid facilitates the computation of the region in RANS and/or LES depending

on the instantaneous conditions existing in the region. Downstream of the rib, in

the region of separation it is observed that the computation is mostly carried out

in the LES model. This sensitizes the RANS model to grid length scales, thereby

Sunden CH006.tex 10/9/2010 15: 39 Page 254

254 Computational Fluid Dynamics and Heat Transfer

allowing the natural instabilities of the ﬂow in this region to develop. Thus, the

unsteady physics in the separated region is captured accurately.

In spite of its attractiveness and successful application, extension of DES to a

wide range of ﬂows poses several challenges [69]. DES is a strategy that depends

onthegridnotonlyforaccuratelyresolvingtheturbulenceintheregionsofinterest,

butalsoindeterminingtheswitchbetweenRANSandLES.Thoughguidelineshave

beenprescribed forSA-based DES(Spalart [70])in externalﬂows,grid generation

ininternalﬂowsisnot trivialand requiressomea prioriknowledge oftheﬂow. One

probable alternative is the scale adaptive simulation (SAS) approach suggested by

Menter et al. [71, 72] that compares a von Karman length scale to the turbulent

length scales to make the RANS-LES switch independent of the grid.

DES still depends on the prediction capability of the base RANS model to

predict phenomena such as separation, transition, and effects of secondary strain

rates due to rotation and buoyancy forces. In previous investigations it has been

found that while DES was successful in capturing secondary strain effects, which

the base RANS model did not capture when used in RANS or URANS mode ([73,

74]), it also failed to predict shear layer transition in contrast to LES which was

successful [75].

The transition from URANS to LES still remains a “grey area” in DES. The

physicsbehindtheswitchfromacompletelymodeledsolutionintheRANSregions

to a well-resolved LES still remains to be understood [76].

6.9 Solution of Linear Systems

Solution of linear systems generated in the semi-implicit and implicit treatment

of the momentum equations and the pressure equation requires careful consid-

eration because these take up a majority of the computational time. The system

matrix ingeneralized coordinates with second-orderapproximations issparse with

18 off-diagonal bands on nonorthogonal grids and can either be symmetric or

nonsymmetric. A symmetric system is only generated on orthogonal grids in the

semi-implicit treatment of momentum and in the pressure equation, whereas the

implicit treatment of convection always leads to a nonsymmetric system. Non-

conformal block boundaries can further lead to strong asymmetries in the system

matrix. There are a variety of methods for solving large sparse systems of linear

equations (Meurant [77]). Out of these methods, iterative Krylov subspace meth-

odshaveproventobequiteefﬁcientforCFDapplications(Barrettetal.[78]).While

the method of conjugate gradients (CG) is useful for symmetric systems, methods

like BiCGSTAB and GMRES(m) can be applied to nonsymmetric systems (Tafti

[79]). Preconditioning can be applied using a variety of methods. One particular

framework that is quite effective is based on a two-level additive/multiplicative

Schwarz domain decomposition (DD) method (Smith et al. [80]; Dryja and

Widlund [81]). In this method, the full system of equations is substructured into

smaller sets of overlapping domains, which are then solved individually in an iter-

ative manner, all the time updating the boundaries such that the global system is

Sunden CH006.tex 10/9/2010 15: 39 Page 255

Time-accurate techniques for turbulent heat transfer analysis 255

110

500

1000

MFLOP/S

1500

2000

100 1000

Block size

Intel lll (1 GHz)

Itanium l (800 MHz)

IBM Power4 (2.3 GHz)

Intel Xeon (3.06 GHz)

Intel Itanium 2 (1.3 GHz)

Apple G5 (2.3 GHz)

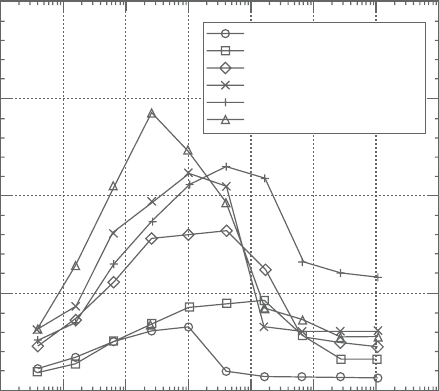
Figure 6.13. Effect of substructured block size on single-processor performance

on some modern computer chips. MLOP, million ﬂoating point

operations.

driven to convergence. Each subdomain is smoothedwith an iterative method such

astheJacobimethodorsymmetricsuccessiveover-relaxation(SSOR)orincomplete

LU (ILU) decomposition.

Not only does the DD method act as an effective preconditioner for the Krylov

method, but also results in large performance gains on modern computer architec-

tures. By substructuring the large system into smaller systems that are designed to

ﬁt into cachememory, main memory accesses are minimized, which result inlarge

performancegains[82–84].Figure6.13showstheeffectofthesub-structuredblock

size on performance with an additive Schwarz preconditioned conjugate gradient

(ASPCG) algorithmfor solving a linearsystem generated bya Laplace equationin

Cartesian coordinates.

Figure 6.13 shows that there is an optimal block size that depends on the pro-

cessor speed, cache size, speed and memory bandwidth, and latency. For very

small blocksthecachelines are not utilized effectivelyand the overhead of getting

data from memory exceeds the equivalentnumberof ﬂoating point operations per-

formed on the data.As the block size increases, the overhead of memory accesses

is amortized over more ﬂoating point operations on block data in cache, and hence

performance increases till the block size gets so large that data required by the

iterative solver for a given block does not ﬁt in cache and has to be accessed from

mainmemorymultipletimes–onceagainincreasingtheoverheadofdatareadsand

stores and decreasing performance. The asymptotic performance beyond a block