Ames W.F., Harrel E.M., Herod J.V. (editors). Differential Equations with Applications to Mathematical Physics
Подождите немного. Документ загружается.

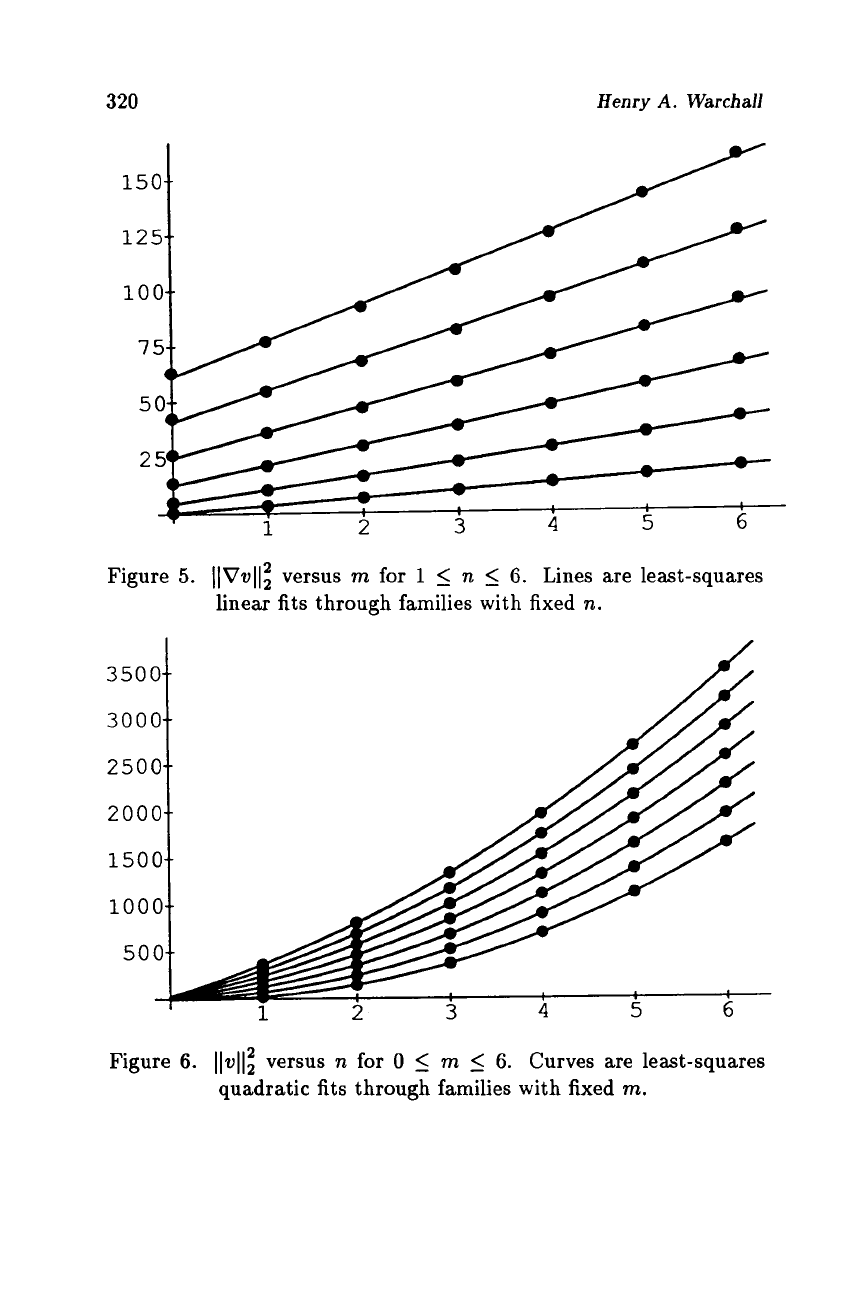
320
Henry
A.
Warchall
1501
1254
Figure
5.
3500-
3000-
2500--
2000-
1500-
1000-
500-
~l~vlli
versus
m
for
1
5
n
5
G.
Lines are least-squares
linear fits through families with fixed
n.
I
5
6
1
2
3
4
Figure
6.
11vl1i
versus
n
for
0
5
m
5
6.
Curves are least-squares
quadratic fits through families with fixed
m.
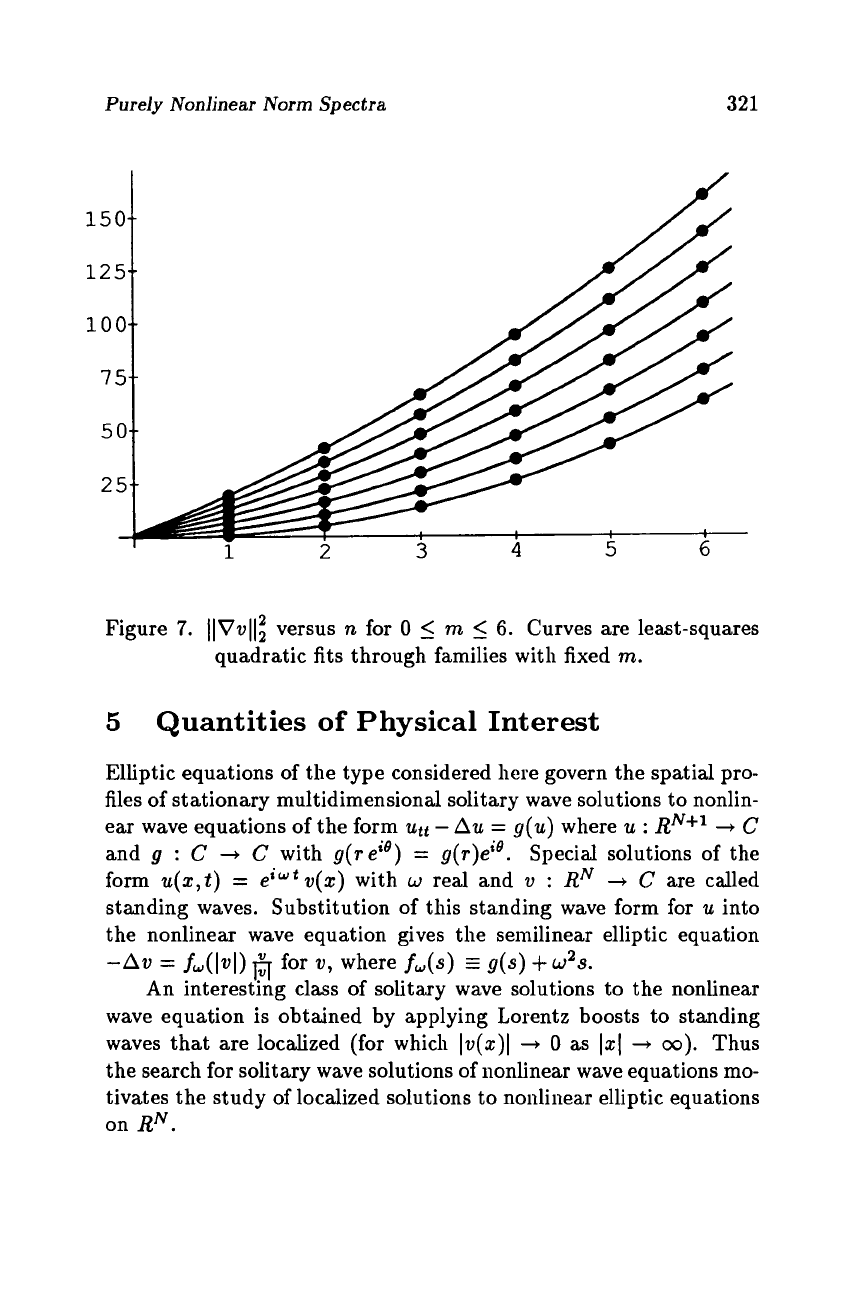
Purely Nonlinear Norm Spectra
321
Figure
7.
llVvl[i
versus
n
for
0
5
m
5
6.
Curves are least-squares
quadratic fits through families with fixed
m.
5
Quantities
of
Physical Interest
Elliptic equations of the type considered here govern the spatial pro-
files of stationary multidimensional solitary wave solutions to nonlin-
ear wave equations of the form
utt
-
Au
=
g(u)
where
u
:
RN+l
+
C
and
g
:
C
-+
C
with
g(reie)
=
g(r)eie.
Special solutions of the
form
u(z,t)
=
eiwtv(z)
with
w
real and
v
:
RN
--+
C
are called
standing waves. Substitution of this standing wave form for
u
into
the nonlinear wave equation gives the semilinear elliptic equation
-Av
=
fw(lvl)
for
v,
where
fw(s)
I
g(s)
+
w2s.
An interesting class of solitary wave solutions to the nonlinear
wave equation is obtained
by
applying Lorentz boosts to standing
waves that are localized (for which
Iv(x)I
--+
0
as
1.1
+
KI).
Thus
the search for solitary wave solutions of nonlinear wave equations mo-
tivates the study of localized solutions to nonlinear elliptic equations
on
RN.

322
Henry
A.
Warchall
Among the conserved quantities
for
solutions of the nonlinear
wave equation are energy
charge
Q[u]
3
JRN
Im[-Gtu]
dx,
and angular momentum
L[u]
JR~
{
x
x
Re
[-fit
Vu]
}
dx.
The values
of
these functionals evalu-
ated
on
standing wave solutions are interpreted as the (rest-frame)
mass, charge, and spin, respectively, of the associated solitary wave.
Explicitly, these physically meaningful quantities are related to the
purely nonlinear norm spectrum of the elliptic equation
as
follows.
The solitary wave mass is
E
=
w2
Ilvlli
+
IIVvlli.
The solitary wave
charge is
Q
=
w
11~11;.
The solitary wave spin is
I
L
I
=
lmwl
Ilvlli.
(We note that nonspherical solitary waves necessarily carry nonzero
angular momentum in the rest frame.)
The purely nonlinear norm spectrum
of
the elliptic equation
is
thus reflected in the discrete set of allowed values
of
solitary-wave
masses, charges, and spins. Thorough understanding of the relation-
ship between the nonlinearity
f
and its norm spectrum will shed light
on the relationship between the dynamics
of
solitary waves and the
structure
of
the solitary wave family in nonlinear wave equations.
B
iblio
grap
hy
111
H.
Berestycki
&
P.-L.
Lions,
Nonlinear scular field equations,
I
and
11.
Arch. Rat. Mech. Anal.
82 (1953) 313-375.
[2]
M.
Berger,
Nonlinearity and Functionul Analysis.
Academic
Press, New
York
(1977).
[3]
C.
Jones
&
T.
Kupper,
On the infinitely many solutions
of
a
semilinear elliptic equation.
SIAM
J.
Math. Anal.
17 (1986) 803-
835.
[4]
P.-L.
Lions,
Solutions complexes d’equations elliptiques semilin-
eaires duns
R”.
C.R.
Acad. Sc. Paris
302
(#19)
(1986) 673-676.

Purely Nonlinear Norm Spectra
323
[5]
W. Strauss,
Existence
of
solitary waves in higher dimensions.
Comm. Math. Phys.
55
(1977) 149-162.
[6]
E.
Deumens
&
H.
Warchall,
Explicit construction
of
a11
spheri-
cally symmetric solitary waves
for
a
nonlinear wave equation
in
multiple dimensions.
Nonlin. Anal.
T.
M.
A.
12 (1988) 419-447.
[7]
G.
King,
Explicit multidimensional solitary waves.
University
of
North Texas Master’s Thesis, August
1990.

This page intentionally left blank

On
Gelfand-Dickey Systems
and Inelastic Solitons
Rudi Weikard
Department
of
Mathematics
University
of
Alabama
at
Birmingham
Birmingham,
AL
35294,
USA
1
Introduction
The Boussinesq equation
is known to have
so
called N-soliton solutions, i.e., solutions that
exhibit asymptotically (as
t
-,
fm)
N
solitary waves of the typical
sech2-form (see Hirota
[5]).
IIere
I
am mainly interested in (a scaled
version of) the Boussinesq equation in imaginary time, specifically,
22
1
Utt
=
--(u
)zz
-
-uzzzz.
3 3
This equation renders “inelastic solitons”, i.e., solitary waves of the
sech2-form which may stick together after interaction thus forming
a
new sech2-wave (see Figure
1).
These inelastic solitons can be obtained via an auto-Backlund
transformation for the Gelfand-Dickey system associated with the
Differential Equations
with
Copyright
@
1993
by Academic Press, Inc.
Applications
to
Mat hernat
i
cnl
All
rights
of
reproduction in any
form
reserved.
Physics
ISBN
0-12-056740-7
325

326
R
u
di
Weikard
Boussinesq-type equation.* In the following
I
will define what Gel-
fand-Dickey systems and their “modified” counterparts, the Drinfeld-
Sokolov systems, are. Section
2
then reviews the above mentioned
auto-Biicklund transformation (see
[3]
and
[4]).
Section
3
describes
briefly (details will appear elsewhere) how the inelastic solitons are
constructed.
Gelfand-Dickey systems are most easily defined in terms of Lax
pairs. By
a
Lax pair is meant
a
pair of two ordinary differential
expressions
an-2
L
=
a:
+qn-2
+
...
+qo,
P
=
a;
+
pr-2a;-2
+
...
+
Po,
which are almost commuting, i.e., their commutator
[P,
L]
is
a
dif-
ferential expression of order
n
-
2
only. Under an additional homo-
geneity condition it is always possible to find uniquely coefficients
pj,
j
=
0,
...,
T
-
2
such that this holds (Wilson
[7]).
This distinguishes
between
n
and
T
and causes the two operators to play very different
roles. The Lax equation
dL
dt
-
=
[P,
L]
is then equivalent to
a
system of nonlinear evolution equations which
is called
a
Gelfand-Dickey system. In particular the well-known KdV
equation is recovered in the case
n
=
2
and
T
=
3,
while the case
n
=
3
and
T
=
2
yields the Boussinesq-type equation
(1).
An important ingredient in the construction of the auto-Backlund
transformation is another system of evolution equations, the Drin-
feld-Sokolov system which is defiiied as follows: Given functions
q$(z,t),
i
=
1,
...,
n
such that their sum is identically equal to zero,
‘As
I
realized only after finishing this
work
these solutions were obtained
earlier by Tajiri and Nishitani
(J.
Phys.
SOC.
J.,
51:3720-3723, 1982) and by
Lambert, Musette and Kesteloot
(Inv.
Prob.,
3:275-288, 1987) using different
methods. However, the construction
of
these solutions in the present context
should be viewed as an illustration
of
how the auto-Backlund transformation of
Section
2
works.

On Gelfand-Dickey Systems and Inelastic Solitons
construct the matrix
M=
0
........
0
ax
t
4n
a,
+
41
........
0
0
0
........
0 0
0
........
ax
+
4"-1
0
327
Then
M"
=
diag(L1,
....
Ln)
where each
Lj
has the form of the above
L:
Note that Lj is obtained from Lj-1 by commuting the first
n
-
1
factors with the last one. This basic idea of commutation goes back
to Darboux and was used by Deift
[l]
to construct the N-soliton
solution of the KdV equation.
Now let
Q
=
diag(Pl,P2
.....
Pn)
where
Pj,
j
=
1
.....
n
is the
uniquely defined differential expression
of
order
T
that almost com-
mutes with L;. Then
is equivalent
to
a
system of
n-
1
non1inea.r evolution equations, called
the Drinfeld-Sokolov system
or
modified Gelfand-Dickey system.
2
An Auto-Backlund Transformation
Given
a
solution of the Drinfeld-Sokolov system, i.e.,
a
set of
4j,
j
=
1,
....
n
such that dM/dt
=
[Q,
A{]
then it is easy to see that this
implies d(Mn)/dt
=
[Q,
Mn],
which
is
equivalent to
This means one has found
n
solutions
of
the associated Gelfand-
Dickey system. This observation is due to Sokolov and Shabat
[6].
Now the following question arises:
Is
it possible
to
reverse this process

328
Rudi
Weikard
and to construct
a
solution
4j,
j
=
1,
...,
n
of the Drinfeld-Sokolov
system given
a
solution of the Gelfand-Dickey system?
If
so
then
one has immediately
n
-
1
new solutioiis
of
the Gelfand-Dickey
sys-
tem.
It
is precisely this question which was answered affirmatively
by Gesztesy and Simon in
[2]
in the case of the I<dV equation and
by Gesztesy, Race and myself in
[3]
in the case of
a
Boussinesq-type
equation.
The answer in the general case
was
given in
[4].
The method there
allows
the coefficients of
L
to be matrices with entries in some com-
mutative algebra with two independent derivations.
For
simplicity,
however,
I
give in the following the scalar version using just functions
of
x
and
t
as coefficients of
L.
Theorem
1
(Gesztesy, Race, Unterkofler,
W.)
Suppose that
(qn-2,
...,
qo)
is
a
real-valued solution of the Gelfand-Dickey system.
Also
assume that the
q;
and their x-derivatives up to order
r
+
i
are
continuous functions
in
R2.
Let
$1,
...,
$n
be
a fundamental system
of
solutions
of
L.11,
=
0
and
.11,t
=
P$
and define
...,
4,
according
to
where
Wo
=
1
and
wk
=
W($l,
...,
$k),
the Wroiiskian
of
$1,
...,
$k
for
k
=
1,
...,
n.
(Note that this implies that
q!Ik
=
0.)
Then
(41,
...,
&)
satisfies the Drinfeld-Sokolov system. Furthermore de-
fine
qk,;,
k
=
1
,...,
n,
i
=
0,
...,
n
-
2
through
(2).
Then each tuple
(qk,n-2,
...,
qk,O)
satisfies the Gelfand-Dickey system.
In particular
(qlpz-2,
...,
ql,o)
=
(qn-2,
...
q0)-
One can allow for an “energy” parameter
X
and consider
L.11,
=
All,
instead of
L.11,
=
0.
The method can
now
be applied repeatedly to
construct new solutions in each step, i.e., new operators
Lj,l
=
Lj-1~
starting from
a
given
Lo,J.
This way
one
may derive the following
formula

On Gelfand-Dickey Systems and Inelastic Solitons
329
In general the solutions constructed by the method described
above may have singularities since the Wronskians used may have
zeros. In the KdV case
as
well as
in
the Boussinesq-type case it
is possible to show that under certain conditions the new solutions
inherit some properties from the original solution.
Theorem
2
(Gesztesy,
Race,
W.)
Let (q1,qo)
be
such that the
Gelfand-Dickey system for
n
=
3,
r
=
2
is satisfied. Furthermore
assume that
q;,...,q!3+i)
are
in
Co(lR2)
n
L"(lR2) and that L$
=
0
is disconjugate at time
to.
Then L$
=
0
is
disconjugate at
ull
times. Moreover, for
a
suitable
choice of a solution system
($1,
...,&),
the
solutions constructed
in
Theorem
1
satisfy the same smoothness
cmd
boundedness conditions
as the original one,
in
particular there
ure
no
locul singularities.
A
similar result was proven by Gesztesy a.nd Simon
[2]
for the KdV
case.
3
Inelastic Solitons
A
solution of the Gelfand-Dickey system for
n
=
3
and
r
=
2
2
Qlt
=
2qoz
-
Qlm,
clot
=
qoxx
-
+.,,
+
41Qlr)
yields at once
a
solution of the Boussinesq- type equation
upon letting
u
=
(4ql
+
3b)/u
(a
#
0).
The
Lax
pair associated to
this Gelfand-Dickey system is
2
3
L
=
82
+
Ql&
t
clo,
p
=
8:
+
-q1.
Starting now from the trivial solution where both coefficients
q1
=
q1,l
and
qo
=
q1,o of
L
=
L1
are consta.nt, new nontrivial solutions of
the Boussinesq-type equation are constructed. The coefficient
q2,l
of
LZ
is given in terms of one solution
$1
of
L$
=
0
and
P$
=
t,bt
as
Q2,l
=
Ql,l
+
3(1%
$l)m
