Ames W.F., Roger C. Nonlinear equations in the applied sciences. Volume 185
Подождите немного. Документ загружается.


100
Shui-Nee Chow
and
Masahiro Yamashita
i
=
1,
...,
m.
Here
z"(v)(t)
=
r(t;a,€'(v,rlz"(a,v,e)))
is the solution of
(3.4)
and
is given in
(5.6).
Similarly
z'(v)(t)
and
'14
is given in
(5.7).
Now it is reasonable
to
define the following quantities.
z(t;a,C"(v,rl;(a,v,e)))
is the solution of
(3.3)
Definition
5.1.
The Melnikov vector
M(a,
v,
e)
for system
(2.2)
is
defined by
where
(5.13)
The first approximation
&'(a)
of the Melnikov vector
M(a)
is defined by
(5.14)
A2(a)
=
(A21(a),...,A2m(a))
where
m
(5.15)
=
J_,
d:(t)g(t
-
a,r(t))dt,
i
=
1,.
.
.
,
m.
Remark
5.2.
M(a,
v,
e)
=
k(a)
+
O(le1)
uniformly in
v.
Remark
5.3.
By
(5.10)
the dimension
m
of
the Melnikov vector
for
system
(2.2)
is the same
as
the number
of
linearly independent bounded solutions
of
the adjoint
system
(5.9).

Geometry
of
the Melnikov Vector
101
Remark
5.4.
The above argument to derive the Melnikov vector is essentially the
same
as
the Lyapunov-Schmidt reduction. However, we employed the above more ele-
mentary and geometrical argument which will be useful when we derive the condition
for the transversal intersection.
Next we consider transversality of the intersection of the stable and unstable
manifolds. Recall from Remark
3.2
that
W&(%-,
c)
and
Wic(F+,
e)
are diffeomorphic
to the graphs
F"(a,q;,r$)
and
P(a,
qf,
q;)
respectively in
a
tabular neighborhood
of
-y
which are given by
and
ER
It
is
clear that transversal intersection occurs when column vectors in the following
matrices
D(u,qy,q;)Fu
and
Du,q;,q;)Fa
at
a
point of intersection span the whole space

102
IR"
:
Shui-Nee
Chow
and
Masahiro Yamashita
Now we have the main result
in
this paper.
Theorem
5.5.
Assume that system
(2.1)
bas
two hyperbolic critical points
x+
and
x-
(not
necessarily distinct) and has an orbit
y
connecting them:
y(t)
+
x+
as
t
--t
00
and
y(t)
--t
x-
ast
+
-m.
Let
k
=
dim{R(I-Q(a))nR(P(a))},
m
=
dim{R(I-Q(a))+
R(P(a>)}l
andlet
v=
(V~,...,V~-~)
E
{R(I-Q(a))nR(P(a))}nT~o,R",
where
P(a)
and &(a)
are
respectively projections of exponential dichotomies
on
(a,
001
and
on
[-00,a)
of system
(3.2)
and satisfy the conditions
in
(3.9).
Consider the perturbed

Geometry
of
the Melnikov Vector
103
system
(2.2)
and define the Melnikov vector
M(a,
u,
E)
and its first approximation
M(a)
by
(6.30)-(6.33).
Then
(i) the cross sections
W'(z+,e)
and
W"(%-,e)
at t
=
0
of the time dependent stable
and unstable manifolds of system
(2.2)
intersect each other if and only if
M(a0,
VO,
e)
=
0
for some
a0
and
vo,
provided
e
ti
suficiently small.
In this case,
(ii) the intersection of
Wl",,(s-,e)
and
WL,(%+,e)
are transversal if there ezist
m
nonzero column vectors in the
m
x
k
matriz
Proof.
(i)
If
M(a0,
po,
e)
=
0
for some
a0
and
UO,
then it
is
obvious from the definition
of
the Melnikov vector that
W;b,(?+,e)
and
Wr",,(s-,e)
intersect each other. Con-
versely, once
W'(?+,
e)
and
W"(%-,
e)
intersect, then there is
a
bi-infinite sequence
{p;}~o=-oc
of
points
of
intersection which approaches
5+
and
5-
as
i
+
+oo
and
i
-t
-oo
respectively. Hence for sufficiently large
lil,p,
E
WL,(?+,e)
n
Wr",,(?-,e)
which implies that
M(a0,
uo,
e)
=
0
for some
a0
and
UO.
(ii) Consider column vectors in matrices
(5.16)
and
(5.17).
Firstly, it is clear that
all
column vectors in blocks
(3)
and
(6)
are always linearly independent. Secondly, by
(5.11),
M(ao,vo,e)
=
0
implies that
Imi(ao)
-
mZ"(a0)l
=
IGl(a0,
uo,rlzd(ao,
e), e)
-
Gi(a0,
vo,
rlZy(a0,
uor
e),
€)I
=
O(lel).
so

104
Shui-Nee Chow
and
Masahiro Yamashita
j
=
1,.
. .
,k
-
1.
Therefore
if
&M(aO,vO,e)
#
0,
then
&(fi;
-
fi;)
#
0
and hence j-th column
vectors in blocks
(2)
and
(5)
are linearly independent at the point of intersection.
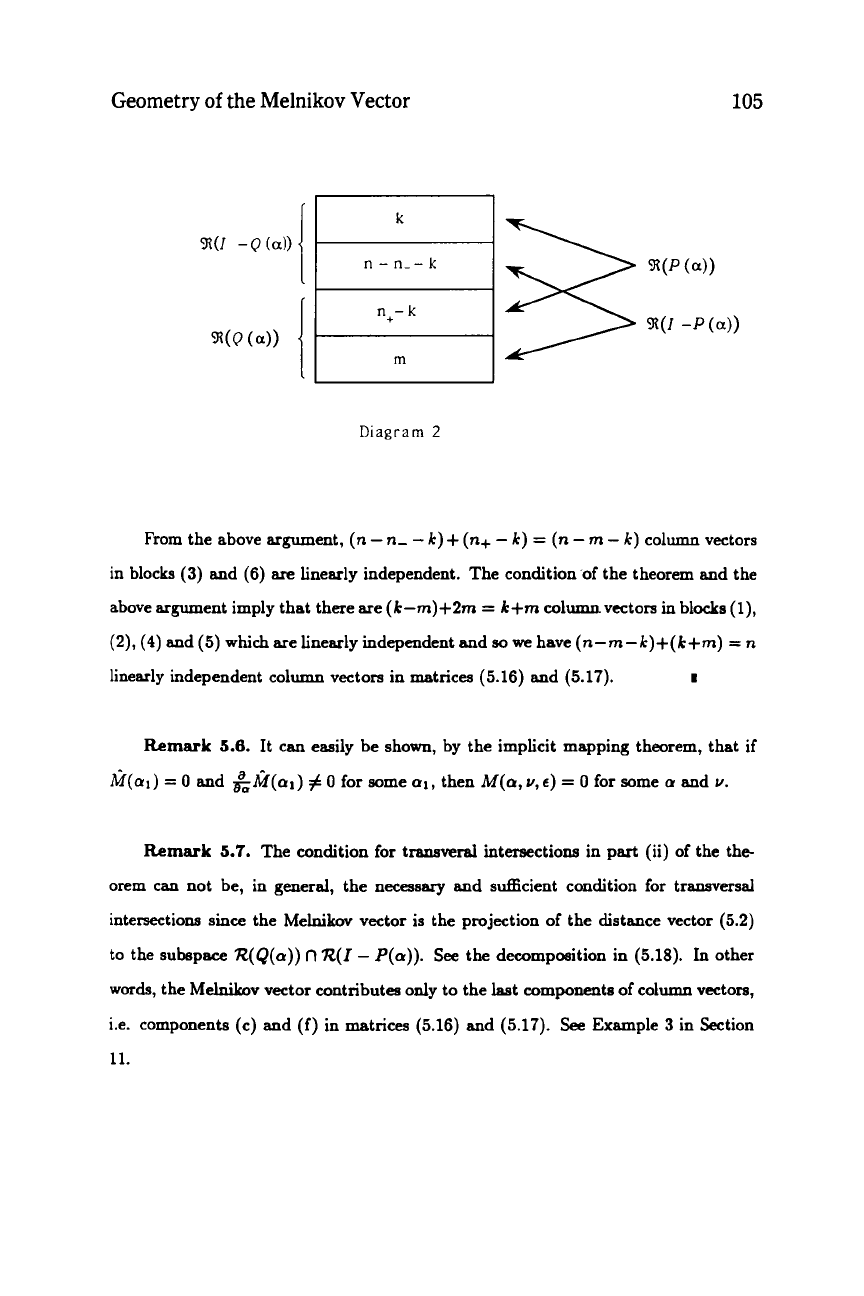
Now consider the following decomposition of
T,(,)R".
@
{R(Q(a))
n
R(P(a)))
@
{R(Q(a))
n
R(I
-
p(a))I
with the following dimensions:
dim{R(I- &(a))
n
R(P(a))}
=
k,
dim{R(I- &(a))
n
R(I
-
P(a)))
=
n
-
n-
-
k,
dim{R(Q(a))
n
R(P(a))}
=
n+
-
k,
dim{R(Q(a))
n
R(I
-
P(a))}
=
m,
where
n-
=
dim
W'(z-)
and
n+
=
dim
W'(z+).
See
diagram
below.
Geometry
of
the Melnikov Vector
105
k
I
I
n-n--k
I
m
Diagram
2
From the above argument,
(n
-
n-
-
k)
+
(n+
-
k)
=
(n
-
rn
-
k)
column
vectors
in blocks
(3)
and
(6)
are
linearly independent. The condition,of the theorem and the
above argument imply that there are
(k-m)+2m
=
k+m
columnvectors in blocks
(l),
(2),
(4)
and
(5)
which are linearly independent and
80
we
have
(n-m-k)+(k+m)
=
n
linearly independent column vectors in matrices
(5.16)
and
(5.17).
I
Remark
5.6.
It can easily be shown, by the implicit mapping theorem, that
if
fi(a1)
=
0
and
&&f(al)
#
0
for some
al,
then
M(a,v,c)
=
0
for some
a
and
v.
Remark
5.7.
The condition for transveral intersections in part (ii) of the the-
orem can not be, in general, the necessary and sufficient condition for transversal
intersections
since
the Melnikov vector is the projection of the distance vector
(5.2)
to the subape
R(Q(a))
flR(1-
P(a)).
See
the decomposition in
(5.18).
In
other
words, the Melnikov vector contributes
only
to the
last
components of column vectors,
i.e. components (c) and (f) in matrices
(5.16)
and
(5.17).
See
Example
3
in Section
11.

106
Shui-Nee Chow
and
Masahiro Yamashita
However. if
the components
(a),
(b), (d) and (e) of column vectors of matrices
(5.16)
and
(5.17)
are
missing and hence the Melnikov vector can be used to give
a
necessary and sufficient
condition for transversal intersection. Thus, we have the following
Corollary
5.8.
Under the same assumption
as
in Theorem
5.5
and assumption
(5.19),
the intersection
of
Wl",,(z-,e)
and
W:oc(5+,e)
is transversal
if
and only if
M(a0,
VO,
e)
=
0
for some
(YO
and
vo
and there exist
m
nonzero column vectors in the
m
x
k
matrix
We remark that condition
(5.19)
implies
m
=
n
-
k.
$6.
THE
SPLITTING INDEX
OF
7
AND
THE
DIMENSION
OF
THE MELNIKOV VECTOR
In this section we define an index
of
a
homoclinic or heteroclinic orbit
7.
Then
this index is used to classify the possible cases of the transversal intersection of the
stable and unstable manifolds. We also interpret this index
as
the Fredholm index of
a
certain operator.
Consider system
(2.1)
and assume that
7
c
Wy(z-)nW"(s+)
is
a
homoclinic or
heteroclinic orbit joining hyperbolic critical points
z*
of system
(2.1).
Definition
6.1.
The splitting index
b(y)
of
a
homoclinic or heteroclinic orbit
7
is

Geometry
of
the Melnikov Vector
107
defined by
(6.1)
b(7)
=
dim
Wa(z-)
-
dim
Wa(z+).
Notice from (5.10) and diagram
1
in
$5
that the dimension
m
of the Melnikov vector
is given by
m
=
n
-
[{n
-
dimWa(z-)}
+
dimWa(z+)
-
k].
Thus
m,
k
and
b(7)
satisfy the following relation.
(6.2)
m
=
k
+
b(7).
The splitting index
6(7)
expresses the 'degeneracy' of
7
in the following sense.
Here we distinguish the homoclinic and heteroclinic cases.
(i) Suppose that
7
is
a
homoclinic orbit. Then the splitting index
b(y)
is always
zero. Thus by theorem 5.5(ii), all of
k
column vectors in
[&
n
M&M]
must be
nonzero to guarantee the transversal intersection. This situation is only the
case
in
the homoclinic case.
(ii) Suppose that
7
is
a
heteroclinic orbit in
R".
In this case we have three
different situations.
(ii-1)
b(7)
>
0.
Then
m
=
k
+
b(7)
>
k.
Thus theorem 5.5(ii) implies that
there is no transversal intersection because the matrix
[&!&$A41
is
of
size
m
x
k.
A
reason for this is that dimWa(z+)
<
dimWa(z-) is equivalent to saying that
dimWU(z-)
+
dimWa(z+)
<
n.
(ii-2)
b(7)
=
0.
In this case we have the same situation
as
in the homoclinic case.
(iii-3)
6(7)
<
0.
Then
m
=
k+b(~)
<
k.
Thus transversal intersection is possible.
In this way, we can classify the possibility and impossibility of transversal intersection
by using the splitting index
b(7).

108
Shui-Nee Chow
and
Masahiro Yamashita
Though the splitting index
b(7)
is defined by local data, that is, the dimensions
of
stable manifolds of hyperbolic critical points,
b(7)
is
global in nature since it can
be used to distinguish homoclinic and heteroclinic orbits, and
also
used to classify
heteroclinic orbits. firthermore, the relation
(6.2)
shows how the dimension
of
the
Melnikov vector depends on
7.
Next we shall show that the splitting index
b(7)
is the Fredholm index
of
a
certain
differential operator defined below.
Let
A(t)
=
Df(r(t))
and define
a
differential operator
L
:
BC'(R,R")
+
BCo(R,
R")
by
(6.3)
(Lz)(t)
=
i(t)
-
A(t)z,
where
BC'(R,R")
is the space
of
bounded
C'
functions from
R
to
IR"
and
BCo(lR,R")
is the space of bounded continuous functions from
R
to
R".
As
we
shall show,
L
is a Fredholm operator.
See
also
Palmer
[16].
Recall that the Fkedholm
index
of
a
linear operator
L
is defined by
index
L
=
dim(ker
L)
-
codim(Range
L)
Proposition
6.2.
The differential operator
L
defined in
(6.3)
is
Fkedholm and
6(7)
=
-index
L.
Proof.
Define a bounded linear operator
A
:
BCo(R,
R")
-+
R"'
by

Geometry
of
the Melnikov Vector
109
where
4i,
i
=
1,.
.
.
,
m
are independent bounded solutions of the adjoint system
6
+
A*(t)4
=
0.
Then Lemma
4.1
and
4.2
imply that RangeL
=
Kernel
A,
which means
that Range
L
is closed and
codim(Range
L)
=
m,
and hence
L
is
a
hdholm
operator. Thus
index
L
=
dim(ker
L)
-
codim(Range
L)
=k-m
=
-6(7).
I
Remark
6.3.
The splitting index
6(~)
in
(6.1)
was defined in Sacker
[18]
in
a
more
general setting and Proposition
6.2
was also proved there. However,
his
definition is
for
linear systems.
Our
definition of the splitting index is to relate
a
local informa-
tion about eigenvalues
of
of(.*)
to
a
global information about
a
homoclinic
or
a
heteroclinic orbit.
57
Computation
of
Higher
Order
Terms
In the
case
of
dim{R(P)(a))
n
R(I
-
&(a))}
>
1
for
n-dimensional systems
(n
2
3),
we need to know nonlinear terms in expression
(5.13)
of the Melnikov vector
to examine the transversality condition. To this end, we consider again bounded
solutions on
[a,=)
and on
(-=,a]
of system
(3.1).
We use the same assumption
of
exponential dichotomies
as
in
53.
These bounded solutions are given
as
unique
solutions
of
integral equations
(3.3)
and
(3.4)
respectively.
Let
qa
E
R(P(a)),lqaI
<<
1,
and let
z(qa)(t)
be the unique solution of
(3.3)
which is guaranteed by the contraction mapping principle. That is,
z(qa)(t)
is the
solution
of
the following integral equation:
