Antontsev S.N., Kazhikhov A.V., Monakhov V.N. Boundary Value Problems in Mechanics of Nonhomogeneous Fluids
Подождите немного. Документ загружается.


108
Chapter
3
-91
2
I
11
VJl
,-,(Q)dt
<-
C(N)
9
0
-9
(1.14)
<-
C(N) (it should be noted that
w;(O
ST)
which denotes that
IIwl(l
the constant
C(N)
is,
generally speaking N-dependent, i.e. this
estimate
is
not uniform with respect to
Nj.
Therefore, the vector
w1
=
Ato
has been established to belong to the class
iVi(0,
T)
and, in line with the theorem of imbedding L121
1,
it
means that the
image
of
the set
K
is
compact
in
C(0,
I).
Besides, the continuity
of the operator
A
results from the theorems on a continuous de-
pendence of the solutions of the Cauchy problem (l.ll*) on the co-
efficients and the right-hand part of
Thus,
it
has been established that the operator
A
satisfies all
the requirements
of
the Shauder theorem, and, hence, has a fixed
point
3
=
(wl
,
.
.
.
,
wN) on the set
K.
The uniqueness of the
so-
lution to problem (1.8)
-
(1.12)
is
proved in a conventional way:
for the difference of two possible various solutions one formula-
tes a homogenious problem, then an estimate of type (1.13)
is
de-
duced, showing that the difference equals zero.
Note. While deducing the compactness of the operator
A
estimate
(1.14) was obtained under the supposition that the function
Ill(t>l[
,Q
is
quadratically summed on
(0,
I)
while in the condi-
tions
of
theorem 1.1 this function
is
from
Ll(O,
T).
This disba-
lance can be eliminated, for instance, by averaging the function
f(t).
Of
importance
is
the fact that estimates (1.13) depend on
the norm of
f
The a priori estimates (1.13) make
it
possible to choose the sub-
+n
sequences
{U
},
{p"}
-9
[IIO].
+
in
L2,
l(k)
which are to be used below.
such that
-9+
ua
+
u
*-weak in
L
m(O,
T;
J(Q))
and weak in
L2(0,
I;
J'(Q)>,
pn
-9
p*weak in
L
m(Q)
at
n
+
m.
Due to non-linearity of the problem, this information ia not suf-
ficient to carry out a limiting transition in the integral identi-
ties of type
(1.41,
(1.5).
Therefore,
our
next step
is
to demon-
strate the compactness of the sequence
{;"
}
in
L2(k).
3. Lemma on the Compactness of Approximations
Lemma 1.2. For the Galerkin approximations
estimate
{un}
valid
is
the
(1.15)
at an arbitrary
6,
0
<
b
<
T
with the constant
C
independent
on both
n
and
6-

Initial-Boundary
Value
Problems
109
Proof. Let
us
fix
6
and
t,
0
<
6
<
l',
0
5
t
I
T
-
6
and note
that (1.9) and (1.10) yield the following relations for the appro-
ximations
;"(TI,
pn(z),
z
€
Lt, t
+
61'.
(1.16)
=
const (These relations are analogous to formulas (1.6), (1.7)).
Let us then integrate the equality (1.16)
with
respect to
t
possible. -Taking into account the ObViOuB identity
7
from
which
is
to
t
+
6
and
then assume that
;d
=
<"(t
+
6)
-
un(t)
+
-b
pn(t
+
6>un(t
+
6)
-
pn(t)un(t)
=
+
--t
+
=
pn(t
+
6>[un(t
+
6)
-
un(t>J
+
[p"(t
+
6)
-
pn(t)Jun(t),
(1.18)
--t
-9
--t
In
(1.17) let
us
then assume
cp
=
(un(t)*[un(t
+
6)
-
un(t)l),
where
(z
-
b)
--t
is
a
&did scalar product, foliowed by the in-

110
Chapter
3
Substituting this relation into
(1.18)
and making use
of the
perty
m
<-
pn
5
M
we get the following inequality
pro-
10
h=
1
+
un(t)l)}
dxdz
s
C
Ilc(t),
(1.19)
where
Integrating
(1.19)
with respect to
t
monstrate that for a.ny of the ten addents
Ik(t),
k
=
1,
2,
...,
10.
in
the right-hand
part,
the following estimates are valid
from
0
to
I
-
6
we can de-
(1.20)
with constant
nk
independent of either
n
or
6.
Let
us
consider,
for
instance,
Employing the Hglder inequality and the imbedding of
J’(S2)
in
L,(Q)
we get the relation
(
c
denotes the constants from the theorems
of
imbedding).
Let
us
change the order of integration by setting
tn(t)
E
0
at
t>T,t<O:
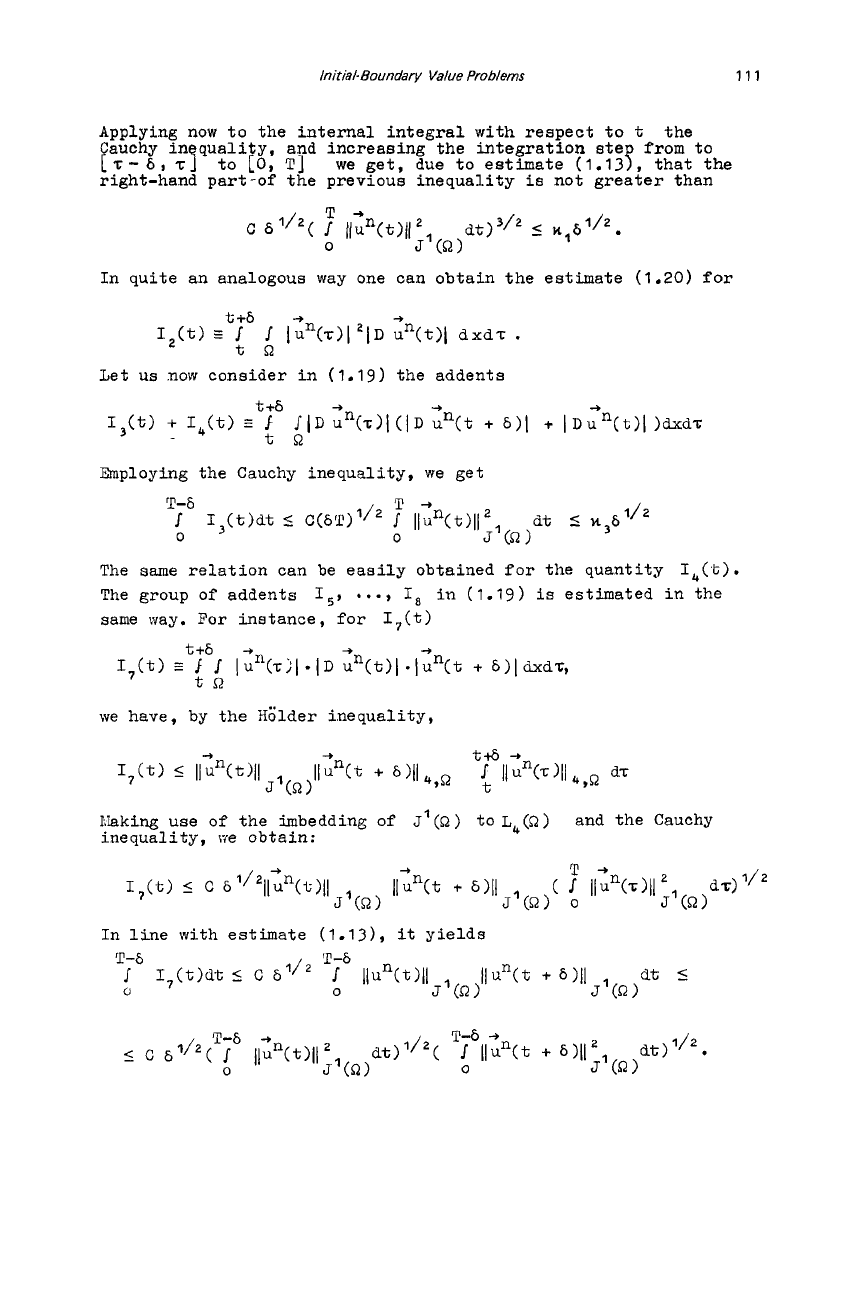
Initial-
Boundary
Value
Problems
111
Applying now to the internal integral
with
respect to
t
the
Cauchy in quality, and increasing the integration ste from to
[?-al
TI
to
[O,
TJ
right-hand part-of the previous inequality
is
not greater than
we get, due to estimate
(1.13P.
that the
In quite an analogous way one can obtain the estimate
(1.20)
for
Let
us
now
consider in
(1.19)
the addents
t+b
+
-b
-?
13(t>
+
14(t>
z
I
,ID
un(7;)1(ID
un(t
+
611
+
lDun(t>l
1dxd-c
tQ
Employing the Cauchy inequality, we get
The same relation can be easily obtained for the quantity
14(t).
The group
of
addents
I,,
a..,
I,
in
(1.19)
is
estimated in the
same way.
For
instance, for
IP(t>
t+6
-b
+ +
17(t>
E
I
1
lun(t>l
*ID
un(t)l
.lun(t
+
6)ldxdg
tn
we have, by the Hzlder inequality,
Llaking use
of
the imbedding of
J1(Q)
to
L4(Q)
inequality, we obtain:
and the Cauchy
In line with estimate
(1.131,
it
yields

112
Chapter
3
In
the
last
co-multiplier, the argument
t
+
6
is
substituted for
by
t,
and the integration step
is
increased to
(0,
T)
in which
case, using the inequality (1.13), we get the required estimate
for the quantity 17(t).
Finally, let
us
consider the last two addents
(1.19):
I,
and
11,
in
In line with the Cauchy inequality,
+
t+
+
lk(t)
<-
IIun(t)ll
J(Q)
I
llf(
")(12,Q
dz
9
k
=
9,
10.
0
It
<-T
t
Changing the order of integration, we find
T-6
t+6
+
T-?
1
.f
Ilf(z)/12,Q
dz
5
6
I
llf(z)ll,,Q
dz,
ot
0
which yields the relation (1.20) for
Therefore, the estimate (1.20) has been established and, hence,
the inequality (1.15) of lemma 1.2 has also been established.
As
a result of this lemma and the
a
priori estimates (1.13) and
according to the theorem
of
imbedding we have the compactness of
the sequence
(3")
in
L,(y)
and in any
of
the domains
L
(k)
with
p
E
[2,
m],
q
E
[2,
6)
4.
The
limiting transition
Using the compactness
of
(u"} one can carry out a limiting tran-
sition
at
n
+
m
in the integral identities (1.4), (1.5)
for
tn
and
p".
blultiplying the equations (1.10) by
with respect to
j
get identit3 (1.4) for
3
functions
cf,
of the type
I,(t)
and Ilo(t).
9P
(see
(SS]).
if
1/p
+
3/2q
>
3/4
--t
H.(t), summing up
J
and cyrying
,put
the integration by parts, we
and
p
which
is
valid for the teat
+"
=
,.Z
Hj(t)zj(x),
Hj(t)
E
C1(O,
T),
H.(I)
=
0.
(1.21
1
J=1
3
Let
us
demonstrate that the
limits
of the obtained subsequences
{itn}
,
{p"}
satisfy identity (1.4) for such
pn
+
p*
is
weak in
L
,(u)
and
u"
+
u
in the norm
L,
(Q,)
the
product
L,(y).
Then, let
us
make sure
that
a.
First, since
pnun weakly reduces
in

Initial- Boundary
Value
Problems
113
-b
For this purpose let
us
present the difference
(pn:n,(:n
-
v)Z?>,,,-
-
(pu,(u
-
v)@),,~
in
the following form
t3
-+
-+t
4
-9-3
4
((pn
-
PlU,
(u
’
vl@12,61
+
(pn(un
-
u),
(u
“El,,,
+
At
n
t
00
the
first
addent tends to zero due to a weak convergence
of
pn
to
p
uniform with respect to
n
boundedness
of
the norms
pn
in
Lrn(Ql2
in
Lm(O,
T;
J(Q)>and due to
a
strong convergence of
un
to
u
in L2(h).In the
two
remaining addents of identity (1.4) for
t”
and
pn
the limiting transition
is
not hampered, since they
are
linear.
It
can be easily shown that at the transition to the
limit
at
n
+
m
the functions
@
in identity (1.4) must have, alongside
with conditions (1.211, the following conditions of smoothness:
while the second and the third ones
-
due to the
-+
un
t
A
set of smooth functions
of
type (1.21)
is
dense in the domain of
functions with the properties (1.22). Therefore identity
(1.4)
is
valid for
all
the functions obeying conditions (1.22). Similarly,
from equation (1.91, by way of multiplying by
cp
and integrating,
followed by the trsnsition to the
limit
at
n
--t
m
we get that
identity
(1.4)
is
valid for all the teat functions ivith the pro-
perties
Thus, Theorem
1.1
is
proven.
2.
DIPFEREIITIAL
PROPERTIES
OF
THE
GENERALIZED
SOLUTIONS
1.
Density continuity with respect to
t
in the integral norms
Lemma 2.1. The
limit
p
of
the sequence
{p”}
from lemma 1.1
is
continuous in the norms L
(a),
1
5
q
<
m
and for all
t
E
LO,
‘i’J
the following equality isqvalid

114
Chapter
3
Proof. Let
us
consider the integral identity
(1.51,
that
is
satis-
fied by
p
:
0
T
-9
J
(P,
'Pt
+
-
VcpI,&dt
+
(P
,
cp(0))2,Q
=
0.
0
+
Let us then extend
u(x,
t)
and p(x,
t)
with the identical zeros
onto the whole of the domain
Q
=
Q
x
(0,
T).
The function
will
then
be
an
element of the space L2(-
a,
+
OD,
J1(R3)),
and the identity
+
u(t)
m
-9
f
(P,
'Pt
+
u
v
'P),,R~
dt
+
(Po,
'P(o)),,~3
=
0
(2.2)
-m
will
hold
at
cp(t>
E
L2(R1;
Wi(R3))
ll
!Yl(R1; L,(R3)),
set
p
(x)
0,
x
E
R3
\
Q
where we
In
(2.2)
let us take a test function
0
cp(t)
in the form of an averaging
I+
where
Q(z>
E
L2(R1;
'ifi(R3)),
Q(T)
=
0
at
0
<
h
<
I.
Let
us
transfer the averaging
o
eration from
8
and
integrate by parts the
first
addent in
(2.215:
T
5
0
and
'c
>
T
-
h,
One
can easily see that the obtained equality
will
be valid for
any function
B(t)
which
is
equal to zero
at
and
is
equal to the arbitrary function
?')(t)
E
L2(tl,t,;
Wi(R3))
at
t
E
(t,,
t,).Here
t,
and
t,
Thus,
t
5
t,
and
t
Z
t,
are any numbers,
05
t,
<
t21
I-h.
-9
Let
us
set here
I
x2
x3
?')
=
WA(X,
t)
z
-
J
J
1
W(E,,
5,,
5,,
t)df
3
A3
XI-A
x,-A x,-A

Initial-Boundary Value Problems
115
-b
and then transfer the averaging again from
w
to
p
and
pu
:
c
Here we denote
-b
It
should
be
noted that the functions
pAh
and (p~)~~
and not zero only in the vicinity of the domain
61
in which case
PAh
2
0.
Let us assume that in (2.3)
w
=
qp;;',
2
<-
q
<
m
Then,
are finite
and (2.3) results the relation
(2.4)
4
Let
us
demonstrate that
if
h
=
O(A
)
then
at
A
-b
0
the right-
-hand part of this formula tends to zero.
It
means that for almost
all
t,,
tz
from
LO,
T]
the equality
is
valid
IIP(t>llq,Q
=
IIP(t1)IIq,Q'
2
5
9
<
m,
(2.5)
since,
by
the property of averaging,
pAh
-b
p
at
A
-b
0,
h
+
0
in
Lq(R3)
almost everywhere on
10,
TI.
To
prove the equality (2.5) let us transform the right-hand part
in
formula
(2.4):
--t
-9
-b
-b
(P')Ah
=
PAh
+
[(Pu>Ah
-
PAh
in which case
u
3
0
outside
51.
The remaining
integral in the right-hand part
of
(2.4)

116
Chapter
3
3
k=
1
is
a
sum
of
three addents
I
=
C
Ik,
Let
us
estimate each of them and make sure that
Ik
-t
0
at
A
+
0.
Let
us,
consider, for instance,
I,.
Applying the estimate
0
I
pAh
<-
hi
and the Cauchy inequality, we deduce:
where
A,
and
A,
denote averaging with respect
to
xp
and x,
with the stepA
b,P
=
P(Xl
+
A,
xz* x3s
t>
-
P(x,, xp) x3g
t>*
Hence,
Let
us
demonstrate that in
(2.6)
the quantity
'
11
(pul)Ah
-
PAh
ulll
2
,RT
if estimeted from above
Z
5
C
A
in
which case the statement that
I,
+O
at
A
-t
0
results from the fact that(/(6,~~)~~~~1,,~~
+o
.
First
of
all, for
Z
the inequality
is
valid
Let make use of the obvious relation

Initial- Boundary Value
Problems
117
and then present the
first
addent
of
the right-hand part of the
EU~
of
integrals
from
the derivatives
Since in
(2.8)
xi
5
ci
5
xi
+A,
A
>
0,
i
=
1,
2,
3
then
Therefore,
-I
In line with the property
of
a generalized solution,
u
E
L2(0,
T;
iiJi(R3))
estimated a8
Couc
hy ine qua1
it
y
and, hence, the
last
addenta in the right-hand part
is
C
A’.The first addent
is
transformed by applying the
In the internal integral over
z
let us make the substitution
t=t)+t:
