Arya S.P.S. Introduction to Micrometeorology

Подождите немного. Документ загружается.

208 13 Marine Atmospheric Boundary Layer

on wind speed,

sea

state, and atmospheric stability. To this end, many

experimental determinations of Co have been made by different investiga-

tors, using different measurement techniques. Early determinations were

largely

based

rather

crude estimates of the tilt of water surface and the

geostrophic departure of flow in the PBL, and are not considered very

reliable. More recently, the sea-surface drag has been determined by

using the more reliable eddy correlation, gradient, and profile methods. A

comprehensive review of the existing data on Co up to 1975was made by

Garratt

(1977). After applying the appropriate corrections for atmospheric

stability

and

actual observation height and using the Monin-Obukhov

similarity relations, the neutral drag coefficient

CON,

referred to the stan-

dard height

10 m, is obtained as a function of wind speed at 10m

) .

Figure

B.4a

shows the block-averaged values of

CON

± 1standard devi-

ation (indicated by vertical bars) for intervals of U

of 1m sec:", based on

the eddy correlation method (closed circles) and wind-profile method

(open circles). The number of

data

used for averaging in each I-m sec"

interval are also indicated above the abscissa axis (the top line refers to

closed circles and the bottom line to

open

circles). Note that there are too

few

data

to give reliable estimates of

CON

at high wind speeds

> 15

ill

sec-I).

Some investigators have inferred the surface stress in hurricanes, using

the geostrophic departure method. Others have measured

CON

at high

wind speeds in laboratory wind flume experiments. Figure

13Ab shows

that

there is a remarkable similarity between the hurricane data and wind

flume

data

(usually referred to a height of 10em, assuming a scaling factor

of 100:

1), despite the large expected errors in the former and dissimilarity

of wave fields in the two cases.

Considering the overall block-averaged data for the whole wide range

of wind speeds represented in Fig.

BAa

and b, there is no doubt that

CON

increases with wind speed. The trend appears to be quite consistent with

Charnock's

formula [Eq. (13.3)], which, in conjunction with Eqs. (10.13)

and (10.14), yields

CON

kCiJW

In(gz/aU2)

(13.5)

After determining the best-fitting value of a = 0.0144 with k =

0041

(for

the more commonly used value of

k = 004, one would obtain a = 0.017,

which is closer to the value indicated in Fig. 13.2), from a regression of In

CON

kCD~2

on In U

Eq. (13.5) is as represented in Figs.

BAa

and b.

In the completely rough regime

> 7 m sec

"),

in particular,

Charnock's

relation is in good agreement with the experimental data. The

variation of

CON

with U

can

also be approximated by a simple linear

relation (Garratt, 1977)

13.2

Momentum

Transfer to the Sea Surface 209

3.0.----,-..,....-,.--,--,--..,..---.----,.---r--....-

.......

(a )

2.0 -

1.01-

16 21 71 43 31 63 56 27 19 5 10 6 I I 3

18 37 56 84 71 51 II 34 18 14 9 6 4 I

2 2

2 4 6 8 10 12 14 16

(m/s

)

18 20 22

I I

I 0

( b )

","""

,..

"'+

t 9

•

3 6 6

5 2 6

5 I

3 I

I I

Z 2

...,

U,O

(m/s)

Fig.13.4

Neutral

drag coefficient as a function of wind speed at a lO-m height compared

with

Charnock's

formula [Eq. (13.5), indicated by the

arrows

in (a) and (b)] with a = 0.0144.

Block-averaged values are shown for (a)

l-rn

sec-

intervals, based on eddy correlation and

profile methods,

and

(b) 5-m sec:" intervals,

based

on geostrophic departure method and

wind flume simulation experiments. [After

Garratt

(1977).]

(0.75 + 0.067U

)

x 10-

(13.6)

or a power relation

= 0.00051

U?046

in which U

is to be expressed in meters

per

second.

(13.7)

210 13 Marine Atmospheric Bonndary Layer

A linear relationship, similar to

Eq.

(13.6), is also suggested by more

recent

measurements

drag in gale-force winds (see, e.g., Smith, 1980).

Such

linear or

power

relations, although convenient for practical applica-

tions, are

not

dimensionally homogeneous (empirical constants must have

rather

odd

dimensions).

Equation

(13.5) suggests that the more appropri-

ate dimensionless

parameter

governing C

is the

Froude

number F

(gZ)1/2,

which should be

used

instead

wind speed.

For

a fixed (standard)

reference height

10 m,

however,

F is directly proportional to the wind

speed

lOV

for V

in meters

per

second) and the latter can be

used for

convenience.

There

is some

controversy

over

the

variation of C

with V

at low and

moderate

wind

speeds

(say, V

< 7.5 m sec

").

At very low wind speeds

< 2.5 m sec: I),

observations

from laboratory flume experiments and

from

over

lakes

and

oceans

indicate a slight tendency of C

to decrease

with

the

increase

in wind

speed,

as would be

expected

for an aerodynamic

smooth surface.

But

sea

surface is rarely completely smooth; ripples and

wavelets

generated

weak

moderate

winds give it a moderate rough-

ness, which is transitional

between

smooth and completely rough re-

gimes.

Some

investigators

have

argued that the

dependence

of C

on V

should be

weak,

if any, in this transitional regime (2.5 < V

< 7.5 m

sec

").

The

data

Fig. 13.4 do suggesta

weaker

dependence

CON

on V

in this range.

Other

oceanic

data

have

even

indicated a nearly constant

value

CON

= 1.2 X 10-

in the

moderate

range of wind speeds (see,

e.g.,

Kraus,

1972).

Dependence

other

parameters,

such as fetch, wind direction

relative to

the

coastline, temporal changes in wind speed and direction,

and

stage

wave

development, also need to be investigated. Most of the

original studies

sea-surface drag do

not

provide quantitative informa-

tion on

these

parameters

and do not classify C

accordingly. Their ef-

fects remain

obscured

the

scatter

of individual

data

sets around the

mean values (indicated by

standard

deviations shown by vertical bars in

Fig. 13.4a

and

b) and also in

the

scatter

mean values.

Few

investigators

have

sought to investigate the

dependence

CON

on wind direction,

fetch,

and

sea-state

parameters,

such as Colu* (see,

e.g.,

Kitaigorodski,

1970;

SethuRaman,

1978; Smith, 1980).

There

is only a slight tendency for

the

drag coefficient to

decrease

with increasing fetch.

has also been

argued

that

the

coefficient a in

Charnock's

formula should decrease with

increasing

Cdu

;

and

may

reach

constant

asymptotic value only at the

equilibrium stage

wave

development. This would imply that

CON

should also

decrease

with increasing Colu*. An observational evidence in

support

such

trend

is given by

SethuRaman

(1978), who also shows

dramatic changes in

CON

response

to a rapid shift in wind direction.

13.3 Parameterization of

Air-Sea

Exchanges

211

13.3 PARAMETERIZATION OF

AIR-SEA

EXCHANGES

In addition to the transfer

momentum between the atmosphere and

the

ocean

at their interface, substantial amounts of heat (both sensible and

latent) and mass (e.g.,

water

vapor, CO

and salt nuclei) are ex-

changed across the

air-sea

interface. Of primary importance to the dy-

namics and thermodynamics of the atmosphere are

the exchanges of heat

and water vapor, which are usually parameterized as

= pCpC

U(0

(13.8)

Eo = pCwU(Qo - Q)

An experimental verification

Eq. (13.8) is given in Figs. 13.5 and 13.6,

in which vertical fluxes of heat and moisture are shown to be well corre-

lated (nearly proportional) with the products

U(0

and U(Qo - Q),

respectively, at a reference height z = 10 m.

Note

that the bulk transfer

coefficients C

and

are given by the slopes of the regression lines

passing through the origin in Figs. 13.5 and 13.6, respectively.

A central objective of many

air-sea

interaction experiments and expe-

" "

0.25

0.20

0.15

-!!!

0.10

0.05

-0.05

-20

100

U(8

o-8).

(mK/s)

120 140

160

Fig.13.5 Sensible heat flux at the sea surface as a function of

U(0

in strong winds

compared with Eq. (13.8) with C

= 1.41 X 10

indicated by the arrow. [After Friehe and

Schmitt (1976); data from Smith and Banke (1975).J

212 13 Marine Atmospheric Boundary Layer

0.18.----------------·-------,

0.15

o POND, SAN DIEGO 1971

n POND, BOMEX

1971

X DREYER, OWAX 1974

" FRIEHE AND

SCHMITT, NORPAX

1974

0.12

+ DUNCKEL ~

'1!.,

ATEX

1974

...,

.!!}

0.09

Q..

0.06

0.03

O.....

....L..----L-

L.-_--'-_--'

...J-_----'

__L_--'

o 10 20

U( Q

-Q

),(m/5)

(g/m

Fig.13.6 Observed moisture flux at the sea surface as a function of U(Qo - Q) compared

with Eq. (13.8) with C

= 1.32 X 10-

indicated by the arrow. [After Friehe and Schmitt

(1976).]

ditions has been the empirical determination of the drag, heat, and water

vapor transfer coefficients (CD, C

and C

), covering a wide range of

surface roughness,

sea

state, and stability conditions. Under moderate

winds (6

< U

< 12 m sec-I) and near-neutral stability, there is an over-

whelming experimental evidence indicating that C

1.2 X 10-

Under

more typical, slightly unstable conditions prevailing

over

the oceans, however, transfer coefficients are somewhat larger, but

still approximately equal to each

other

(CD

1.5 x 10-

) ,

least within the estimated margin of error (±20%) of their determination

(see, e.g., Pond, 1975).

These

results point out to a rather simple parame-

terization of

air-sea

fluxes in terms of wind speed, temperature, and

specific humidity at

the

lO-m level and the sea-surface temperature.

Atypical or exceptional stability conditions may be encountered, of

course,

over

certain oceanic areas and during certain weather conditions

when

Co,

and C

may considerably differ from their above typical

values.

For

example, in the areas and periods of intense cold-air advec-

tion

over

the

warmer

ocean, free convection may occur in which C

and

are expected to become considerably larger than

> 1.5 X 10-

the

other

hand,

under

inversion conditions and light winds, all the transfer

coefficients are expected to become much smaller than their neutral

value.

(13.10)

13.3 Parameterization of

Air-Sea

Exchanges 213

I-

U 2

w....J

ffici

,,-0::

cnl-

z::>

~ ~

1---------=----='----------''\-------1

I-

"-I-

i=1-

0::

-0.4

-0.3

-0.2

-0.1 0 0.1

0.2

RiB

Fig. 13.7 Calculated ratios of the drag and heat transfer coefficients to their neutral

values as functions of the bulk Richardson number and C

•

[After Deardorff (1968).]

The stability effects on the drag and

other

transfer coefficients can be

considered in the framework of the

Monin-Obukhov

similarity theory.

For

example, Eq. (11.16)

can

be expressed in the form

CD/CON

= [1 -

k-lcg~tjJm(z/L)]-2

(13.9)

CH/C

k-lcg~tjJm(z/L)]-l[l

k-lCH~tjJh(Z/L)]-1

expressing the ratios

CD/CON

and CH/C

as functions

CON

and

z/L.

These

can

also be expressed in terms

the more convenient bulk Rich-

ardson

number

RiB

gz(0

o)/T

rJ2

, using the following relations

between

z/L

and

RiB:

z/L = kC

oM2Ri

for

RiB

< 0

L =

WRi

(1 - 5Ri

)- I, for

RiB?

The first of these relations is only an approximation to the more exact but

implicit relationship between

z/L and RiB. The above approximations are

considered to be quite good for the expected range of

RiB

values

(-0.1

RiB

< 0.1)

over

the ocean. The

tjJ

functions in Eq. (13.9) are given by Eq.

(11.14), so that the ratios

CD/CON

and CH/C

can

be evaluated as func-

tions of RiB. Figure 13.7 shows that these are only weakly dependent on

the neutral value of the drag coefficient

(CON),

but have rather strong

dependence on RiB, particularly in stable conditions.

There are very few experimental studies in which stability effects on

the drag and

other

transfer coefficients have been systematically investi-

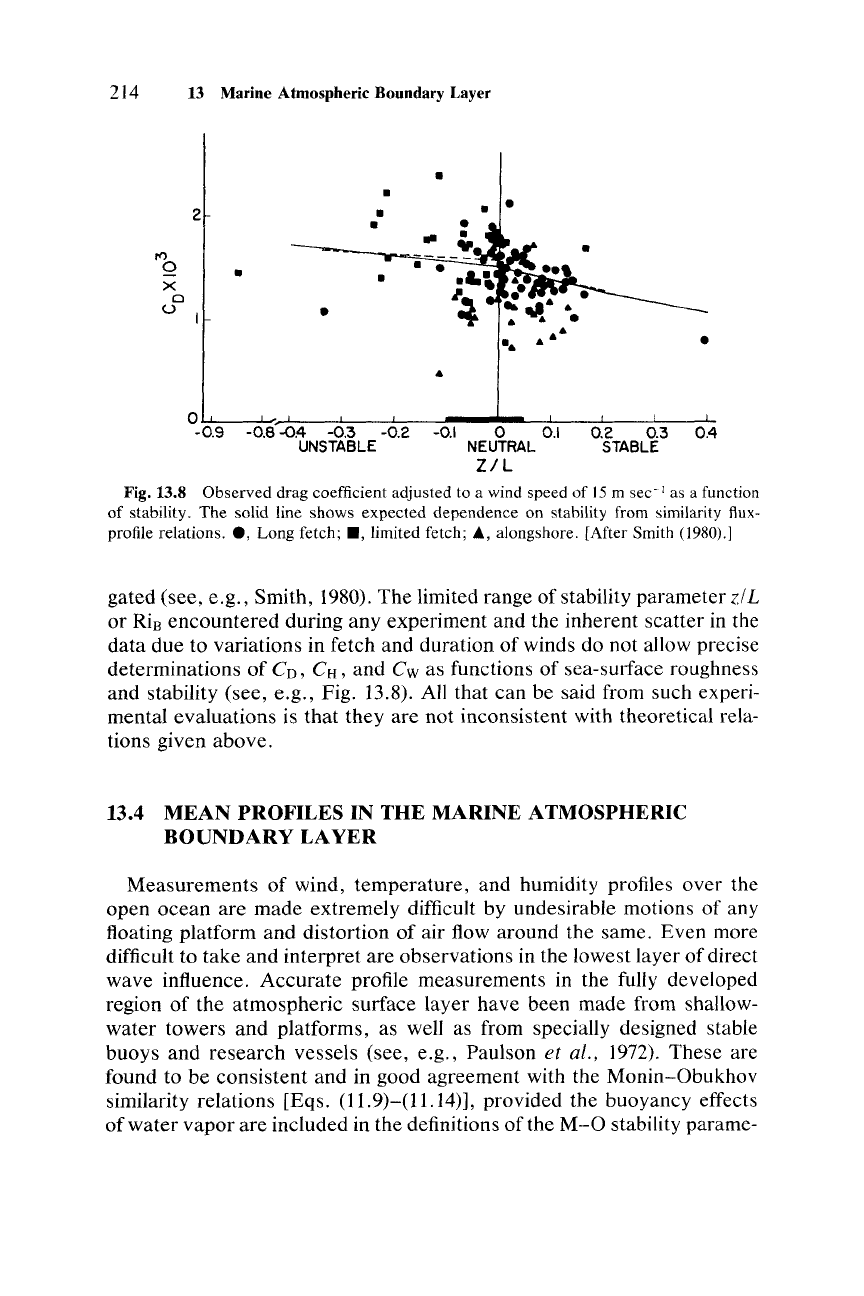
214 13 Marine Atmospheric Boundary Layer

•

;----

•

...

•

-0.9

-0.8-0.4

-0.3

-0.2

-0.1

0 0.1

0.2

0.3 0.4

UNSTABLE

NEUTRAL

STABLE

ZlL

Fig. 13.8 Observed drag coefficient adjusted to a wind speed of 15 m sec-I as a function

of stability. The solid line shows expected dependence on stability from similarity flux-

profile relations. • , Long fetch;

limited fetch; A, alongshore. [After Smith (1980).]

gated (see, e.g., Smith, 1980). The limited range of stability parameter zlI.

RiB

encountered during any experiment and the inherent scatter in the

data due to variations in fetch and duration of winds do not allow precise

determinations of CD, C

and C

as functions of sea-surface roughness

and stability (see, e.g., Fig. 13.8). All that can be said from such experi-

mental evaluations is that they are not inconsistent with theoretical rela-

tions given above.

13.4

MEAN

PROFILES

THE

MARINE

ATMOSPHERIC

BOUNDARY

LAYER

Measurements of wind, temperature, and humidity profiles over the

open

ocean

are made extremely difficult by undesirable motions of any

floating platform and distortion of air flow around the same. Even more

difficult to take

and

interpret are observations in the lowest layer of direct

wave influence. Accurate profile measurements in the fully developed

region of the atmospheric surface layer have been made from shallow-

water

towers

and

platforms, as well as from specially designed stable

buoys and research vessels (see, e.g., Paulson

et al., 1972). These are

found to be consistent and in good agreement with the Monin-Obukhov

similarity relations [Eqs. (11.9)-(11.14)], provided the buoyancy effects

water

vapor

are included in the definitions of the

M-O

stability parame-

13.4 Mean Profiles in the MARL 215

7.0

6.5

6.0

...

5.5

5.0

3 4

(rn/s

)

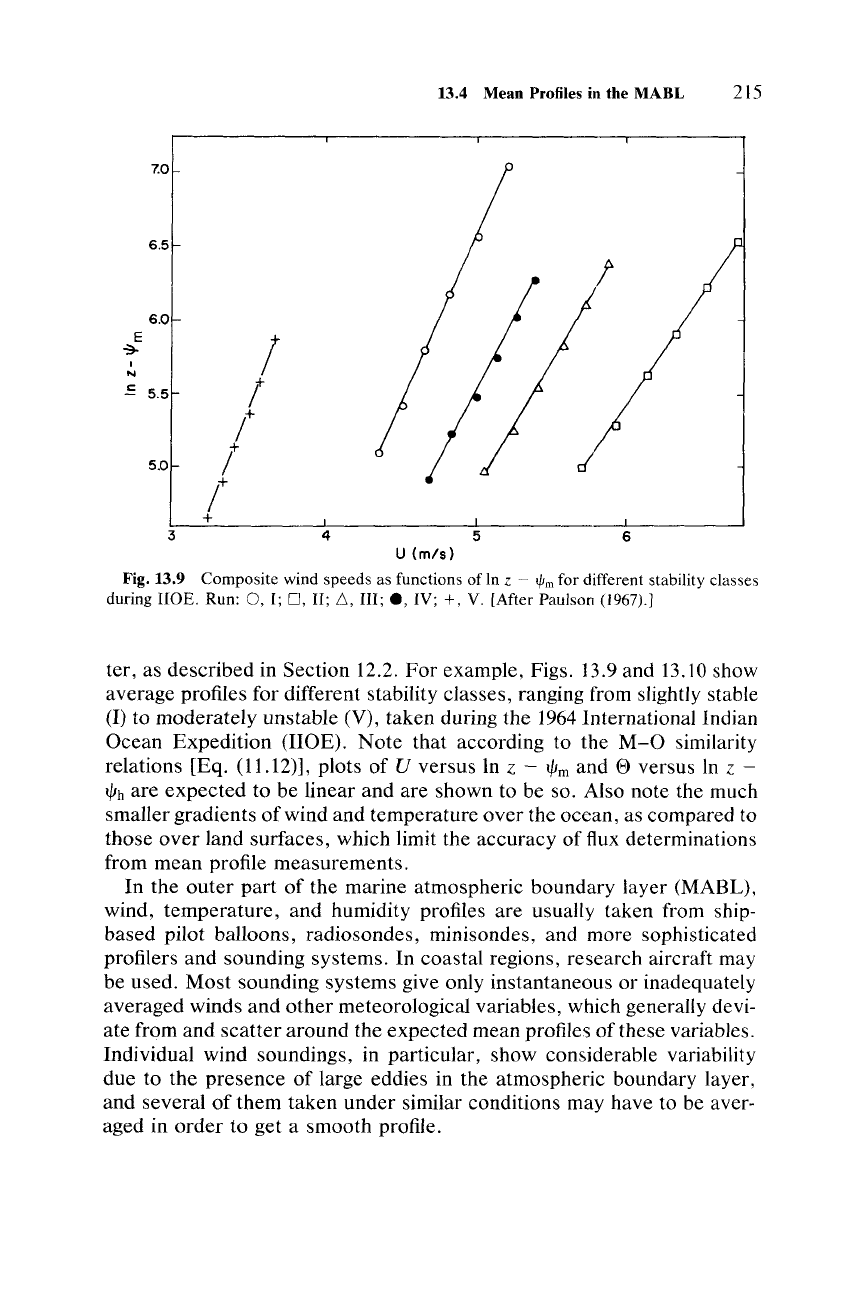
Fig. 13.9 Composite wind speeds as functions of In z

lfJrn

for different stability classes

during IIOE. Run:

I; D, II; L.,

III;.,

IV; +, V. [After Paulson (1967).]

tel', as described in Section 12.2.

For

example, Figs. 13.9 and 13.10 show

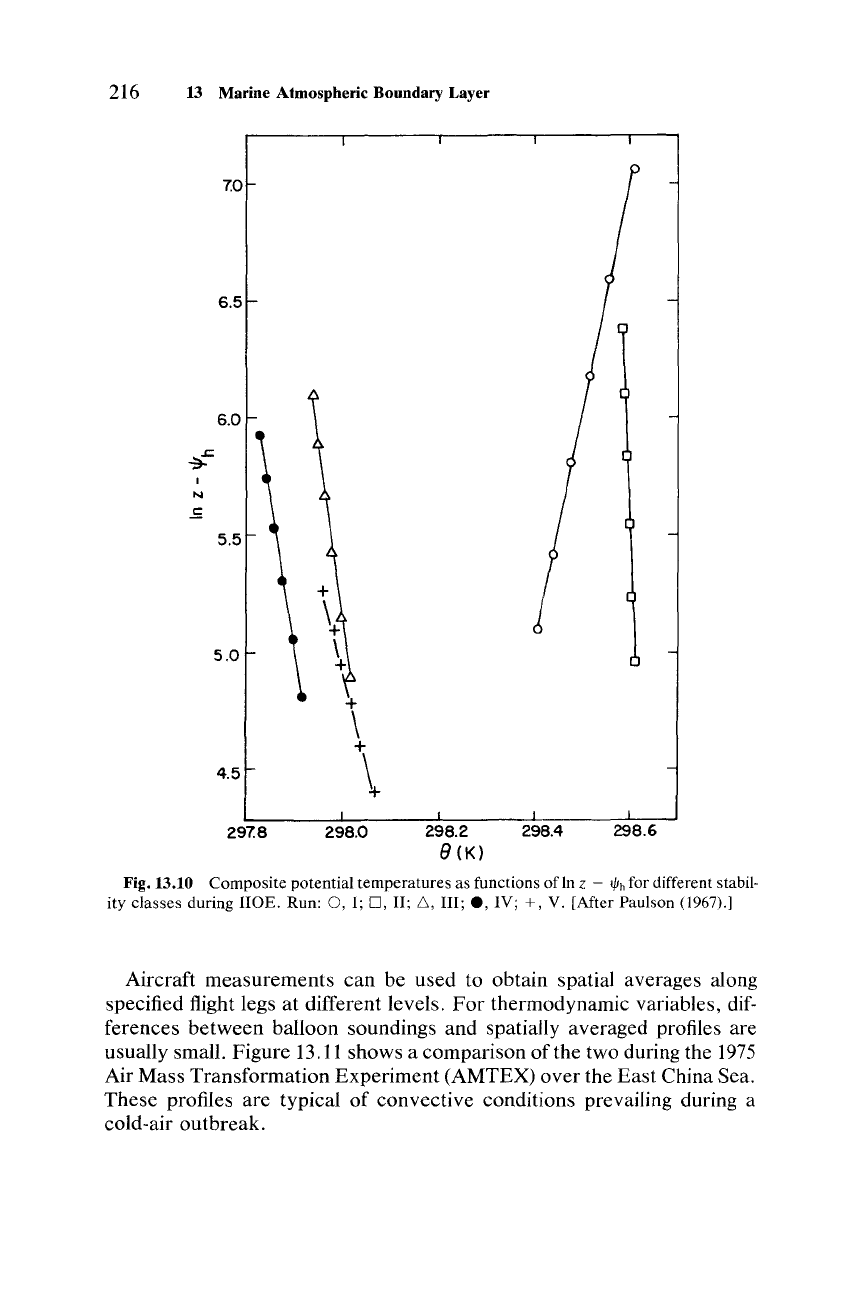
average profiles for different stability classes, ranging from slightly stable

(I) to moderately unstable (V), taken during the 1964International Indian

Ocean Expedition (HOE).

Note

that according to the

M-O

similarity

relations [Eq. (11.12)], plots of

U versus In z -

t/lrn

and ® versus In z -

t/lh

are

expected

to be linear and are shown to be so. Also note the much

smallergradients of wind and temperature

over

the ocean, as compared to

those

over

land surfaces, which limit the accuracy of flux determinations

from mean profile measurements.

In the

outer

part

of the marine atmospheric boundary layer (MABL),

wind, temperature, and humidity profiles are usually taken from ship-

based pilot balloons, radiosondes, minisondes, and more sophisticated

profilers and sounding systems. In coastal regions, research aircraft may

be used. Most sounding systems give only instantaneous or inadequately

averaged winds

and

other

meteorological variables, which generally devi-

ate from and

scatter

around the expected mean profiles of these variables.

Individual wind soundings, in particular, show considerable variability

due to the presence of large eddies in the atmospheric boundary layer,

and several of them taken under similar conditions may have to be aver-

aged in

order

to get a smooth profile.

216 13 Marine Atmospheric Boundary Layer

7.0

6.5

6.0

~L:.

5.5

5.0

4.5

297.8

298.0

298.2

8<Kl

298.4

298.6

Fig. 13.10 Composite potential temperatures as functions of In z -

o)Jh

for different stabil-

ity classes during HOE. Run:

I; D, II;

III;.,

IV; +, V. [After Paulson (1967).]

Aircraft measurements

can

be used to obtain spatial averages along

specified flight legs at different levels.

For

thermodynamic variables, dif-

ferences

between

balloon soundings and spatially averaged profiles are

usually small. Figure 13.11 shows a comparison of the two during the

1975

Air Mass Transformation Experiment (AMTEX)

over

the

East

China Sea.

These profiles are typical

convective conditions prevailing during a

cold-air outbreak.

13.4

Mean

Profiles in the

MARL

217

2000...-----,----,----,----,,..---,-----.----,.------.

1800

1600

1400

1200

1000

800

400

200

~75

2950

---l::>Q--1

Fig. 13.11

Observed

mean

potential

temperature

and specific humidity profiles under

convective conditions during

AMTEX.

Leg average; +, sounding (February 15). [After

Wyngaard

et al. (1978).]

The

potential

temperature

and specific humidity profiles in the MABL

during

typical, slightly unstable,

and

fair-weather conditions are

given in Fig. 13.12.

These

were

measured

by an aircraft during the 1974

GARP

Atlantic Tropical

Experiment

(GATE).

Note

that in the subcloud

layer,

B, By, and, to some

extent,

Q profiles are nearly uniform. The

400

200

1000

(a)

-I-l,-~--('-J~

_\'1:

r r r I t J

l..

l 1 J

12 14

(K)

Q(gm/kg)

Q(gm/

kg)

Fig. 13.12

Observed

mean potential

temperature

and specific humidity profiles in the

marine

boundary

layer

under

slightly unstable conditions during

GATE.

(a) Day 253 and (b)

day

258. [After Nicholls and

LeMone

(1980).]