Avgoustinov Nikolay. Modelling in Mechanical Engineering and Mechatronics

Подождите немного. Документ загружается.

3.1 Problems of Contemporary Modelling 91

it for many of its potential users. But the more complex a given standard is, the

longer takes its adoption and, respectively, implementation. This seems to be the

case with,

e.g., ISO 10303 (well-known as STEP).

3.1.1.12.1.3 Interface

Each standard ages and at some point in time, a need to extend or update it arises.

If this need arises gradually and not simultaneously at all concerned enterprises,

some of the affected developers or users of the standard attempt to introduce

extensions in their implementation of the standard. Thus, different extended

implementations begin to lose their conformity (see the respective section below).

Moreover, with each extension from a different implementer, the standard loses its

role and strength. One of the consequences is that the interfaces to and from such a

standard become inefficient or even non-operational.

3.1.1.12.2 Standard-related Traits

In this section we shall try to define some traits that allow us to assess and compare

different implementations of a given standard. In order to provide a better basis for

comparison, it is preferable for us to define and use traits that can be measured

over the same range – ideally the range [0,1]. Such values can also be interpreted

as percentages.

3.1.1.12.2.1 Conformity of a Standard's Implementation

Let there be a standard defined through a certain set of characteristics S

std

and an

implementation of the standard, defined through the set of characteristics

Simpl

which is a union of the set of implemented elements of the standard

sdtElements

and

the set of implementation-specific elements S

spec

. As a general trait allowing us to

judge how standard-conforming a given implementation is, we can now use the

ratio of the number of implemented elements of the standard and the number of all

elements in the standard:

std

sstdElement

conf

S =

(3.3)

Here S

conf

is the standard conformity, which has a range [0,1].

3.1.1.12.2.2 Specificity of a Standard's Implementation

This trait is not just the inverse value of standard conformity, but also a measure of

uniqueness. Therefore, it is proportional to the number of implemented extra

characteristics (extensions of the standard) and to the number of unimplemented

characteristics, but is inversely proportional to the number of implemented

characteristics.

⎟

⎠

⎞

⎜

⎝

⎛

impl

std

spec

implSpec

(3.4)

3.1.1.12.2.3 Interfaceability of a Standard

It could be interesting to estimate how difficult it is to interface two different

implementations of the same standard, i.e. to establish a way of exchange between

92 3 Conventional Product and Process Modelling

them. This trait, being specific to each set of a given standard and any two of its

implementations, will be called interfaceability and will be denoted

I(standard,source,target). It is proportional to the standard conformities and

inversely proportional to the specificities of the both implementations:

(

)

T)S,(std,

,,,

−−

TSTS

SpSpSCSCfI (3.5)

3.1.1.12.2.4 Standard-related Complexity

No two standards have equal complexity – each standard is specific and has its

peculiarities. Yet, efforts to reduce their complexity are observed. The introduction

of application protocols in STEP, for instance, aims at reducing the complexity by

restricting the scope of each protocol and thus making its implementation easier,

inasmuch as several granules of smaller size are to be considered instead of a huge

one.

3.1.1.12.2.5 Effort for Exchange/Porting

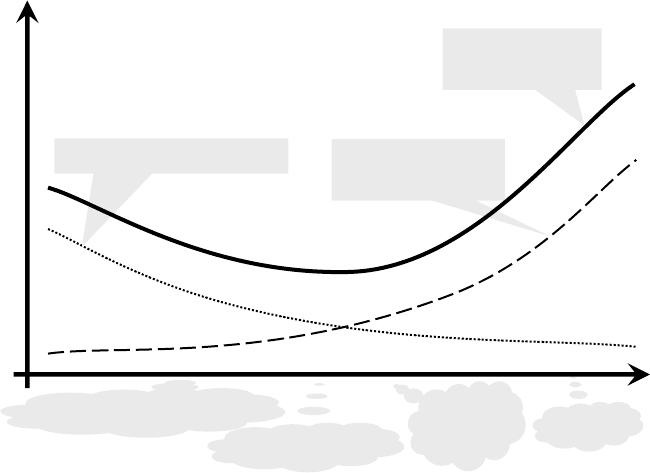
The standards for data exchange are being designed and developed to facilitate the

exchange and make it more efficient. With increased standardization effort,

though, the total effort for exchange and standardization may become bigger than

the effort for exchange without standard. Based on the author's observations, in

Figure 3.5 a hypothesis is presented about the total effort with regard to different

standardization grades. According to this hypothesis the minimal total effort for

exchange is expected to be somewhere between conventions and meta-norms. The

exact position depends on the specific case, scope as well as other factors.

Figure 3.5.

Effort for exchange/porting depending on standardization grade

norms

standardization grade

total effort

for exchange

effort for

standardization

effort

effort for exchange

conventions

recommendations

meta-

norms

3.1 Problems of Contemporary Modelling 93

3.1.1.12.3 Compatibility and Data Exchange

The development of a good standard takes time – everything should be carefully

contemplated, verified, validated,

etc. This time can be so long that the

requirements can change or even a need for a totally new standard could arise. A

typical example here is ISO 10303, whose first version development time took

more than a decade, and even before it was complete, the work on the second

version started. Despite great achievements of ISO 10303, the main problem

nowadays is still the incompatibility of the data formats of different CAx-systems.

On the one hand, it is attempted to overcome the incompatibilities by development

and use of standards for data representation and exchange. On the other hand, in

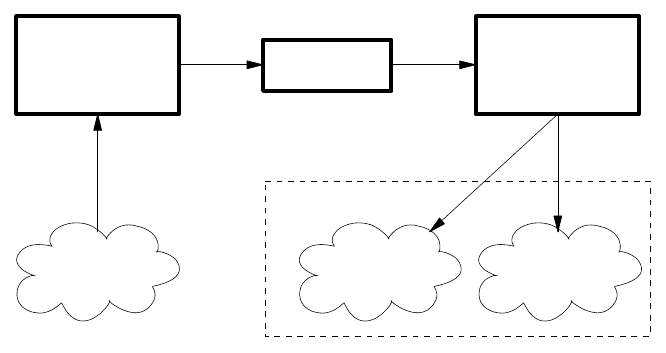
order to integrate models created in different systems, an exchange between the

systems still has to be performed. An exchange using a standard format would just

save the converter (

cf. Figure 3.6) but not the exchange itself. This means that the

mentioned architecture would still have problems with the huge size of the models.

Integrated models "live" in system B

Model A

in format A

Converter

CAx system A

CAx system B

Model B

Model A

in format B

Figure 3.6.

Integration of models by means of data exchange

Note the paradox: STEP’s objective is “to provide a (system-independent, or

neutral) mechanism that is capable of describing product data throughout the

lifecycle of a product, independent from any particular system”, but no CAx-

system producer is even thinking about changing the native format of its CAx-

system to STEP, let alone doing it! This means that either the so-called STEP pre-

processors and postprocessors or the PDM-enablers (or both) have to exist for each

CAx-system type.

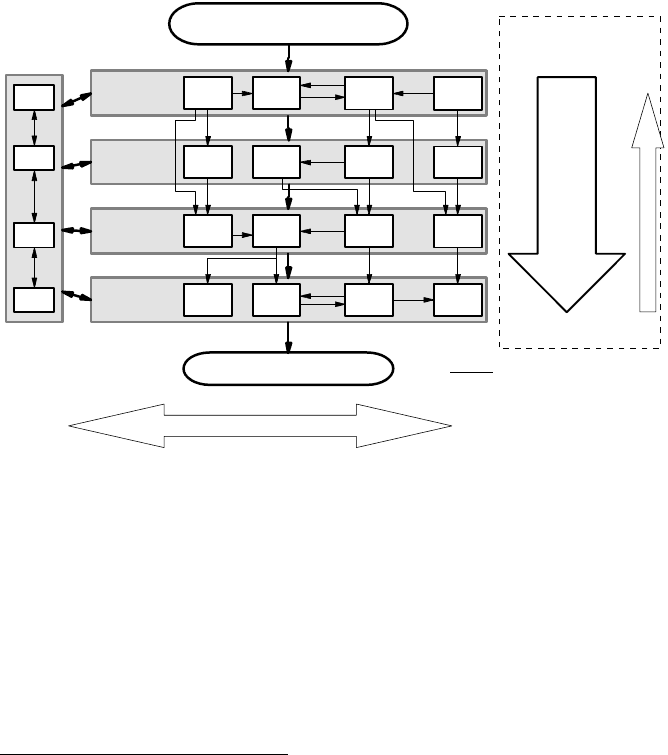
Another point, which is often disregarded, is discussed in Avgoustinov (1997).

It is never the case that all data in a production chain has to be available (and

respectively – converted) to all CAx-systems of the chain. Moreover, due to the

specifics of the information flow it might be more efficient to have distinct

standards for the exchange (

cf. Figure 3.7) within each phase and perhaps a few

standards for inter-phase exchange, rather than having one standard to cover the

whole development and production chain.

Any standard acts as an accelerator up to a given moment in the development,

but after some (the same or other) point in the time it acts conservatively and slows

94 3 Conventional Product and Process Modelling

down the development unnecessary, especially by wrong subject or extent. In

many cases a set of carefully chosen conventions can suffice and be much more

flexible than a standard. On pp.166–167 of Booch

et al. (1999), for instance, it is

suggested that “A well structured interface is

simple yet complete, providing all the

operations

necessary yet sufficient to specify a single service;…” (parts of the

citation italicized by the current author). And the increasing popularity and success

of industry standards like

CORBA

(cf. OMG (1998)), DCOM+

and

Enterprise Java Beans™

confirms again the flexibility and the acceptance of

these alternatives to a “global standardization”.

Inter-phas

(main

)

information flow

PDM

Design phase

Feedback

Product Delivery

Process planning

phase

Manufacturing

phase

Quality control

phase

Customer's Request

Legend:

CAD =Computer Aided Design

CAPP=Computer Aided Process Planning

CAM =Computer Aided Manufacturing

CAQ =Computer Aided Quality control

PDM =Product Data Management

EDM =Engineering Data Management

CAD

CAPP

CAM

CAQ

CAD

CAPP

CAM

CAQ

CAD

CAPP

CAM

CAQ

CAD

CAPP

CAM

CAQ

Main

inform.

flow

PDM

EDM

Intra

hase

(

auxiliar

Information Flo

Figure 3.7. Standardization of the information exchange within a production chain: dividing

in several sub-domains, after Avgoustinov (1997)

3.1.1.13 Other Problems

There are problems related to security, complexity, diversification, heterogeneity,

usability and overall value. Many of them are consequences of globalization,

which intensifies the competition by increasing the pressure of costs, the pressure

of time, the need for cooperative work and, therefore, the need for communication.

Moreover, globalization exposes some specific problems like norm and regulation

diversity among the partners, clash of cultures, as well as some special

requirements. Also not to be ignored is the group of

psychological problems: using

Abbreviated from Common Object Request Broker Architecture.

Abbreviated from Distributed Common Object Model. It is Microsoft’s architecture for

working with distributed objects.

The name of the architecture for working with distributed objects from Sun

Microsystems, Inc.

3.1 Problems of Contemporary Modelling 95

software can be fun, but when the software is unexciting, complex, buggy and

lacks ergonomics, its use can be boring. We should not forget that many new

technologies, products or ideas fail to become popular due to secondary factors like

lack of attractiveness, (critically) high accidental complexity or bad advertisement

and popularization. Quite to the point, Brooks Jr. (1987) spoke about the role of

exciting technologies and their “great designers”. Considering, on the one hand, the

high number of industry standards created by a couple of people but having great

success, and on the other hand, the large number of unsuccessful standards created

artificially by committees, he argues that “we should better learn to

grow great

designers

” than to develop “great” standards and tools (quotation complemented

by the author).

3.1.2 Complexity-related Issues

The challenge over the next 20 years will not be

speed or cost or performance; it will be a

question of complexity.

Bill Raduchel, ~1999

(Chief Strategy Officer, Sun Microsystems)

Our enemy is complexity, and it’s our goal to

kill it.

Jan Baan, ~1999

(SAP competitor)

Simplicity is the ultimate sophistication.

Leonardo da Vinci, 1452 – 1519

The fact that complexity and complexity-related problems have been in the focus

of many investigations from ancient times until today illustrates the importance of

this topic. There exist different views on complexity, methods to oppose it and

even sayings about it. One aphorism says that most genius-made things are simple,

although not all simple things are works of a genius.

According to Brooks Jr. (1987) “

…from the complexity comes the difficulty of

communication among team members, which leads to product flaws, cost overruns,

schedule delays… less understanding … unreliability”

. As complexity leads to

many other problems and inconveniences (cf. Figure 3.4 above), it is very

important to try to analyse the influence of complexity on the modelling and

develop methods to measure and reduce complexity. But what is complexity?

3.1.2.1 Towards a Definition

Although a common word such as complexity should be intuitive enough, a brief

look in the relevant literature shows a wide spectrum of interpretations of this term,

varying from “the opposite of simplicity” to long and domain-dependent

96 3 Conventional Product and Process Modelling

definitions. Furthermore, complexity is discussed in different context by different

authors:

e.g., in Fagade et al. (1998) we find “total product (or project)

complexity”, “management complexity”, “design and manufacturing complexities”

and “process complexity”; or in Edmonds (1999b), offering a study of the

complexity definition by various authors, it speaks of “true complexity”, “real

complexity”, “system complexity”, “observer complexity”, “computational

complexity”, “Kolmogorov complexity”, “descriptive complexity”, “complexity

per se”; Grünwald and Vitányi (2003) use, in addition, “descriptional

complexity”

, “object's complexity”, “algorithmic complexity” and “stochastic

complexity”; finally, we could supplement all these with essential and accidental

complexity after Brooks Jr. (1987) (

cf. previous paragraph and Section 3.1.1.2

above). To summarize, there is no unified view on complexity: scientists could be

distributed into at least three groups according to their understanding of

complexity.

The views of one group (mainly IT-experts) would be, probably, best illustrated

with the definition, given in Black (2005): “

The intrinsic minimum amount of

resources, for instance, memory, time, messages, etc., needed to solve a problem or

execute an algorithm.

” This definition is not tangible enough to use as a base for

(more) quantitative assessments. And since it measures the complexity of a

problem only indirectly, one could get the impression that the complexity depends

on the tool used for its solution, which is unacceptable. Another definition of

complexity in the same sense, but explicitly bound to the (context of) algorithms is

given in Howe (2006): “

The level in difficulty in solving mathematically posed

problems as measured by the time, number of steps or arithmetic operations, or

memory space required (called time complexity, computational complexity, and

space complexity, respectively).

” As we can see, both definitions mainly refer to

computational complexity, which constitutes only one part of the complexity of a

software model.

Another widespread interpretation is that complexity can be viewed as a

measure of the difficulty to understand a given matter or to deal with it. The lack

of understanding alone is not always a problem, but it becomes important as soon

as a decision based on the respective matter has to be taken. Since understanding

can hardly be quantified and, in addition, depends on other factors (

cf. Figure

3.14), such a definition is of little use.

A better alternative is proposed by another group, represented,

e.g. by Suh (cf.

Suh (2001), chapter 9). According to this definition, complexity and information

are tightly related and:

Definition 3.1: Complexity is a measure of uncertainty in achieving

the desired functional requirements.

This definition allows us to measure complexity directly in bits, which is very

convenient and puts the stress once again on the relation to information. Thus, it is

applicable not only to software systems, but to any other system with a countable

number of components. However, it is measured or defined as “

only relative to

what we are trying to achieve and/or want to know

” (cf. Suh (2001, p. 472),

meaning that until the functional requirements are known the complexity either

Cited as used in the source; not to be confused with “descriptive complexity”!

3.1 Problems of Contemporary Modelling 97

does not exist, which is obviously false, or we cannot measure it, which is rather

inappropriate. Yet, complexity according to Definition 3.1 refers only to a part of

the whole complexity phenomenon and should probably be better called

“complexity of achieving the aims”.

Even the simplest technical system or the simplest object can be “finite” only at

a certain level of observation or abstraction. For instance, we are not able to count

the atoms in the smallest mechanical part or in the smallest piece of matter.

Physicists have not succeeded until now to fully explain the structure of the atom

itself. It is (still) impossible to repudiate certain “fractality” of the matter –

cf. the

Bohr model, explained in Wiki (2006) as a planetary model in which the electrons

orbit a tiny nucleus in the way that the planets orbit the sun. Indeed, neither in the

direction of the macrocosm nor in the direction of the microcosm an End comes

into sight, meaning that – as for now – we can hardly dream of final (or countable)

systems. Consequently, the real complexity of anything tends towards

infinity, or at

least is immeasurable. So, Edmonds (1999b) states: “

The “true complexity” of real

objects (if it existed) would probably be totally beyond us

”.

Nevertheless, in our everyday life we perceive certain things as more complex

than others, or some aspects of the same thing as more complex than others –

e.g.,

the use of any product is normally much easier than its development or production.

Moreover, we can deal (although not in all cases) with this “infinite complexity”.

What helps us is our ability to abstract away from the inessential details and deal

with the essentials only. For this reason I shall introduce a new term here:

Definition 3.2: the perceivable or ascertainable part of the absolute (or

full, or total, or overall) complexity of an entity will be

called discernible complexity of this entity.

The term entity is used as a generic term (or placeholder) because it is more

general than model, product, process,

etc. The entity could also be a task – e.g., to

prepare a model or to produce certain product. Therefore, all references made to an

entity within this section could be applied as well to any problem, task, model,

product, process or other complex object.

As already mentioned above, many different complexity types are discussed in

the literature, but no attempt of their systematization or their ordering in a

taxonomy has been available until now –

cf. also Weber (2005c). In my view,

when speaking about one and the same entity, there are no different types of

complexity, but different views or aspects on it.

Definition 3.3: any part of the discernible complexity of a given entity,

which is important or essential, mainly in connection

with something specific or from a specific viewpoint

(aspect) will be called aspect complexity.

Development, use, testing, marketing, etc. are examples of different aspects.

Each aspect appears to be related to (specific) activities, and activities are often

specific to a given phase within the lifecycle. The overall discernible complexity,

which is relevant for a given problem or entity, can thus be viewed as greater than

or equal to the sum of the complexities of all its aspects. In addition to the

discipline-specific aspects there could exist general or product-specific aspects,

too.

98 3 Conventional Product and Process Modelling

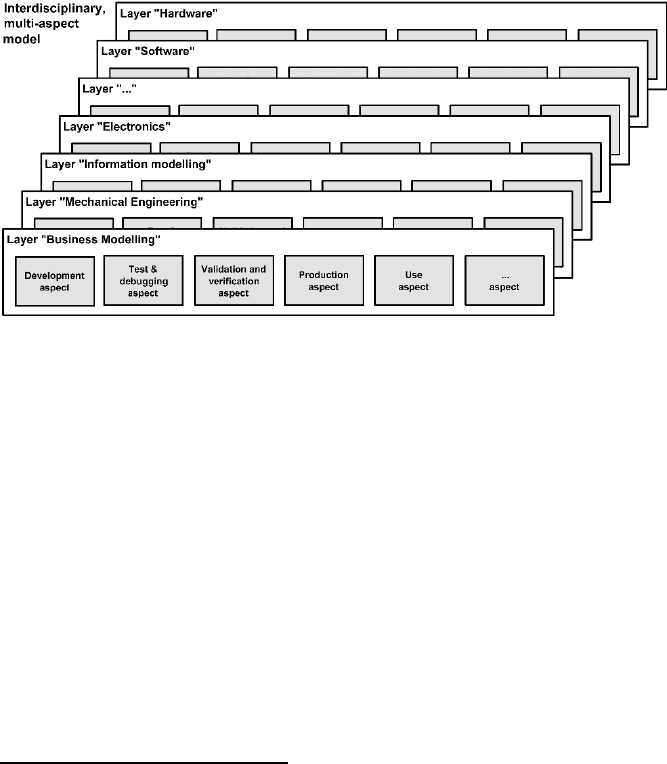
In interdisciplinary branches of science like mechatronics, one or more of the

general aspects may exist in more than one of the involved disciplines, which

additionally increases the complexity. In this text, “discipline” is used as a more

general term than “domain”. To avoid possible confusion, all (or most) discipline-

specific parts of such interdisciplinary models are separated in their own

layer (cf.

the definition of layer in chapter “Modelling basics”).

We could think of aspects and disciplines as of two dimensions forming the

complexity space

of a given entity, as illustrated in Figure 3.8. In fact, there is one

more relevant dimension of complexity that is not considered here, namely,

structure (to be discussed in Section 3.1.2.2.3 below), but it is difficult to prepare

an adequate representation on (two-dimensional) paper.

Figure 3.8.

Complexity of an interdisciplinary model: layers and aspects

Until now, the causes of complexity and the factors influencing it have been

investigated unexpectedly little. So, let us start with some observations.

3.1.2.2 Observations

When we use the word “complexity” alone we actually (unconsciously?) mean

“discernible complexity”. The absolute complexity of software models is always

finite (after all, they are created on computers having final memory and saved on a

medium within finite place), but often it is higher than we can perceive, feel

comfortable with or would like to have.

The brain cannot perceive information having (discernible) complexity above

certain

critical level. This critical level is person-dependent, i.e. the discernible

complexity is subjective. In particular, it depends on the person's

a priori

knowledge (depending in turn on education and background), on the power of

comprehension, and perhaps – at least to some degree – on the training. An

illustration of the different perception of two persons, experts in the same

competence domain, is given in Figure 3.9.

Not to be confused with the term space complexity, used in computer science to refer to

the amount of memory space that a computer program requires for its proper execution.

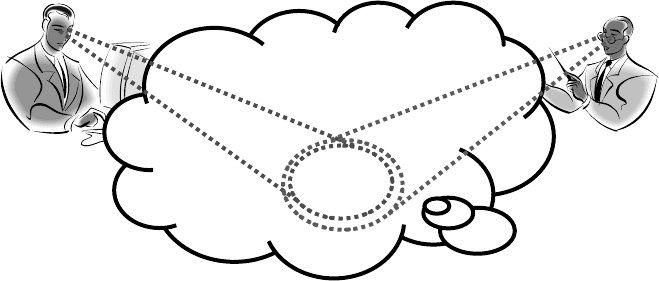
3.1 Problems of Contemporary Modelling 99

Figure 3.9.

Individual limits by perception of complex matter

In order to understand why the critical level of complexity is essential, suppose

that we are observing (only) one person, having to solve a problem or a task in the

considered competence domain – say, to develop a product for us. We call this

person (at least for this example) Solver; and we – as a customer – are permanently

increasing the number of our requirements for the negotiated product.

As expected, with the increased number of requirements the complexity of the

problem increases, too. At the beginning the problem is simple (its complexity is

negligible), and the problem is solved in the best possible way. With increasing

complexity, we reach a point when our Solver starts to produce sub-optimal

solutions (or products). This means that he either cannot find an optimal solution,

or finds multiple solutions but cannot decide which is the optimal one. If we

continue to pose new requirements (and thus further increase the complexity), a

moment will come when the complexity is so high that the Solver cannot control it

anymore, and either delivers a wrong solution or cannot deliver a solution at all.

This stage corresponds to the critical complexity level.

The ability to make (appropriate) decisions as a function of the complexity is

graphically represented in Figure 3.10.

The critical complexity level marks the boundary between solvable and

unsolvable problems, or between ability and inability of making a decision. So it

makes sense to terminologically distinguish whether the complexity is below or

above this level. Since the ability to take decisions is typically related to the ability

to control a given situation, we shall use the terms controllable and uncontrollable

for complexities below and above the critical level, respectively.

In general, a typical sign that the critical level is reached is the fact that the

person in question either ceases to perceive (the excess of) information or cannot

start to perceive it at all. The latter case happens typically when the information

comes from a foreign domain about which very little

a priori knowledge is

available. The additional uncertainty, resulting from the lack of knowledge and

understanding that are needed to solve a given problem, is called

imaginary

complexity

in Suh (2001, p.476).

The imaginary complexity is usually higher when multiple aspects of the

modellee have to be considered. If the discernible complexity of the main aspect of

the modellee is already near to the critical complexity level of the Solver, this

means that every new aspect that has to be considered increases the risk of

Competence domain

Task o

problem

100 3 Conventional Product and Process Modelling

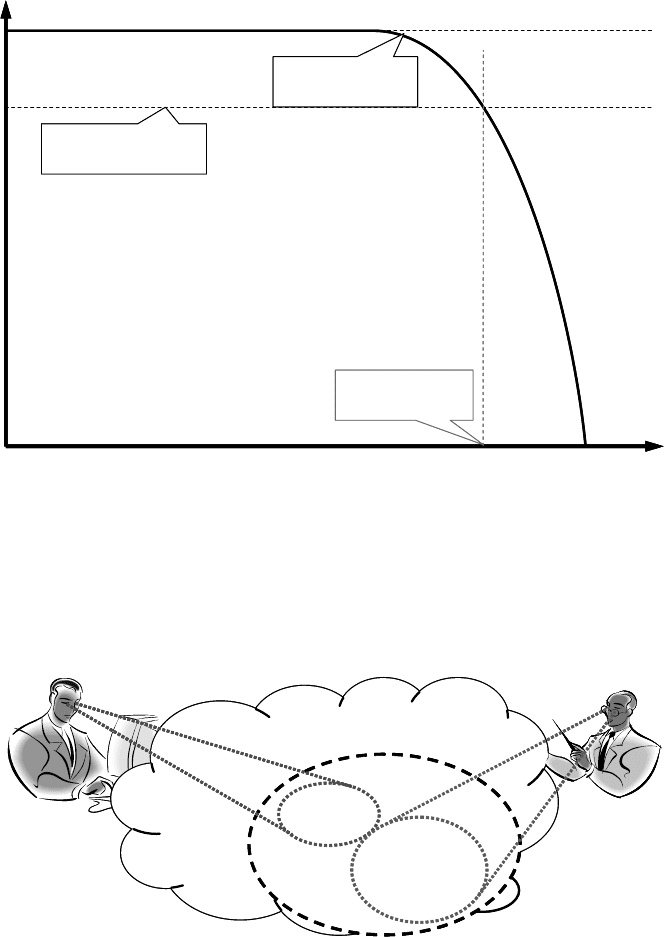
reaching a situation without (optimal) solution. How to deal with this challenge? If

we assume that the critical complexity can be expressed as the number of facts that

are (still) comprehensible at the same moment, one possibility to reduce or keep

the complexity below the critical level is visualized in Figure 3.11.

Complexity

100%

Ability to

make decisions

Critical

complexity level

Critical (in)ability

to make decisions

Complexity

100%

Ability to

make decisions

Critical

complexity level

Critical (in)ability

to make decisions

Figure 3.10.

Dependence of decision making on complexity

The complexity of a process and its results are not necessarily mutually

dependent. Often simple procedures (codes, programs), both in nature and

computing, yield most complex results, and

vice versa – complex procedures

return simple results. Similar observation can be made about the interdependence

of the complexity of a problem and its solution. Therefore, a reasonable question is

what exactly generates and influences the complexity of a model.

Competence domain

Main task

Subtask

Competence domain

Main task

Subtask

Main task

Subtask

Figure 3.11.

Focusing by splitting/reducing the scope to keep the complexity controllable