Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

4.3 Second moments of area 205

Example 4. 5

Determine the second moments of area I

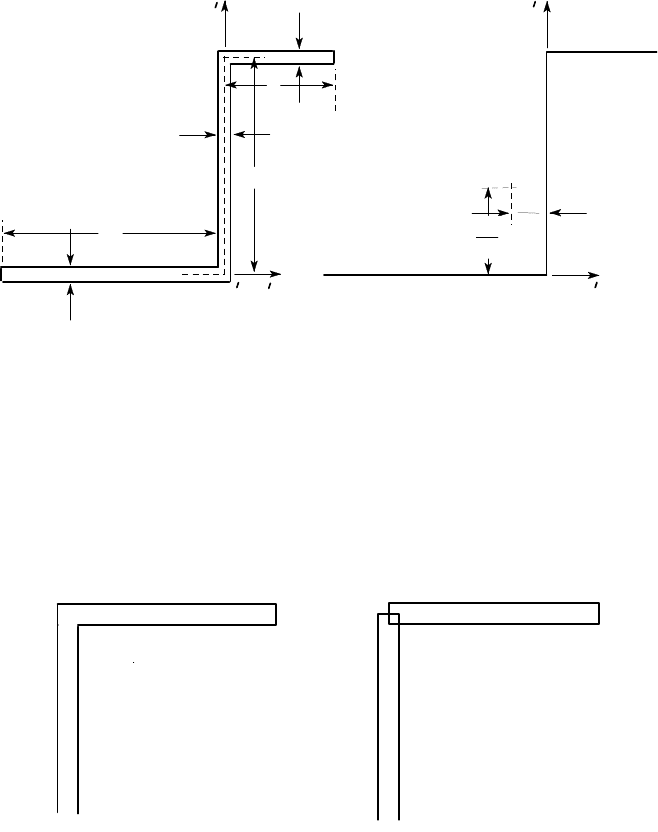
for the unequal Z-section of Figure

4.17 (a), for which t ≪a. The section is deﬁned by the dimensions of the mean line

ABCD which is equidistant between the two sides of the wall. The corresponding

mean line is shown for clarity in Figure 4.17 (b).

A B

(a) (b)

Figure 4.17: (a) The unequal Z-section, (b) the equivalent mean line

We choose to centre the coordinate system O

′

on the point B, as shown in

Figure 4.17 (a). The area of each section is taken to be the product of the length of

the mean line and the section thickness, which has the effect of replacing the actual

corner section CD of Figure 4.18 (a) by the overlapping rectangles of Figure 4.18 (b).

The error involved in this process is clearly of the order of t/a and hence negligible.

(a) (b)

Figure 4.18

206 4 Unsymmetrical Bending

We identify the segments AB, BC, CD as A

respectively, after which we

can construct the ﬁrst ﬁve rows of the table:-

i 1 2 3

segment AB BC CD

2at 2at at

¯x

−a 0

¯y

0 a 2a

( ¯x

− ¯x) −

( ¯y

− ¯y) −

Table 4.3

Equations (4.30, 4.31) then give

A = 2at + 2at + at = 5at

A ¯x = −2a

t + 0 +

= −

A ¯y = 0 + 2a

t + 2a

t = 4a

and hence the coordinates of the centroid are

¯x = −

; ¯y =

as shown in Figure 4.17(b).

We can now complete the remaining rows of the table, noting that the centroidal

second moment of a thin rectangle about its mean line is negligible, since it is of the

order at

≪a

Using equations (4.36–4.38), we therefore obtain

+ 2at



−



+ 2at





+ at





52a

+ 2at



−



+ 2at





+ at





51a

and the product inertia is

4.4 Further properties of second moments 207

= 2at



−



−



+ 2at









+ at







11a

Notice how all these expressions reduce to a numerical multiplier on a

t, since

any other combinations of a,t are small in the sense of t ≪a.

4.4 Further properties of second moments

In addition to the parallel axis theorem, there are relationships between the second

moments of area about axes that are not parallel. These relations give further insight

into the section properties and often enable us to predict how a beam will behave

under given loading without performing more than the simplest calculations.

4.4.1 Coordinate tr ansformation

Suppose we are given I

in some coordinate system Oxy and we wish to ﬁnd

the corresponding quantities I

′

in some other system centred on the same point,

but rotated with respect to the ﬁrst set through an angle

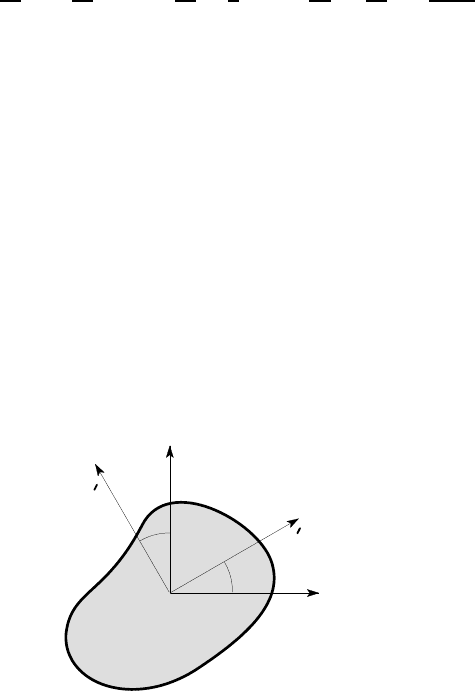
as shown in Figure 4.19.

Figure 4.19: Rotation of coordinate axes

We ﬁrst note that the vector r deﬁning the position of a given element of area dA

can be written

r = ix + jy = i

′

+ j

′

, (4.39)

where i,j, i

′

are unit vectors in the x,y, x

′

-directions respectively.

Using this notation, we can write

′

= r · i

′

= (ix + jy)·i

′

= x(i · i

′

) + y(j · i

′

)

= xcos

+ y sin

. (4.40)

and by a similar argument,

′

= ycos

−x sin

. (4.41)

208 4 Unsymmetrical Bending

D (x,y)

Figure 4.20: Trigonometric construction for establishing equation (4.42)

These results could also be proved using trigonometry as shown in Figure 4.20, since,

for example, x

′

= OB = OA+AB; OA = OE cos

= xcos

; AB =CD = DE sin

ysin

, leading to equation (4.40) as before.

Now, by deﬁnition

′

′2

dA =

(ycos

−x sin

)

dA , (4.42)

using (4.41). Expanding the square in the integrand and separating terms, we then

have

′

= cos

dA −2sin

cos

xydA + sin

= I

cos

−2I

sin

cos

+ I

sin

, (4.43)

using the deﬁnitions (4.15).

By a similar procedure, we ﬁnd

′

(xcos

+ y sin

)

= I

cos

+ 2I

sin

cos

+ I

sin

(4.44)

′

(xcos

+ y sin

)(ycos

−x sin

)dA

= (I

−I

)sin

cos

+ I

(cos

−sin

) . (4.45)

4.4.2 Mohr’s circle of second moments

The perceptive reader will notice a similarity between equations (4.44, 4.45) and the

stress transformation equations (2.1, 2.2), except for some sign differences. In fact

the signs can be made the same by establishing the equivalences

→ I

;

′

→ I

′

(4.46)

→ I

;

′

→ I

′

(4.47)

→ −I

;

′

→ −I

′

. (4.48)

4.4 Further properties of second moments 209

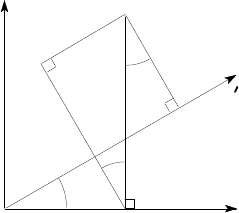
It follows that we can draw a Mohr’s circle for I

′

as shown in Figure 4.21.

X ( , )

Y ( , - )

Figure 4.21: Mohr’s circle for second moments

With the convention used here, clockwise rotation around the circle will corre-

spond to clockwise rotation of the axes about which the second moments are calcu-

lated.

Some important consequences

It follows immediately that:-

(i) There are two principal axes, labelled 1,2 in Figure 4.21.

(ii) About these axes, the product inertia I

=0.

(iii) About these axes, I

is a maximum (point 1) or a minimum (point 2). We shall

refer to axis 1 as the stiff axis and axis 2 as the ﬂexible axis for the beam. They

are respectively the axes about which it is hardest and easiest to bend the beam.

(iv) Since I

′

> 0 for all

— it is the result of integrating a squared quantity [see

equation (4.44)] — the circle must lie totally in the right half-plane.

As in §2.1.1, the distance to the centre of the circle and its radius are easily shown

to be

c =

+ I

; R =



−I



+ I

(4.49)

[compare with equations (2.5, 2.6)]. Since the circle must lie completely in the right

half-plane (see (iv) above), we must have c >R and hence c

. Substituting from

equations (4.49) for c,R, we therefore have



+ I





−I



+ I

and hence

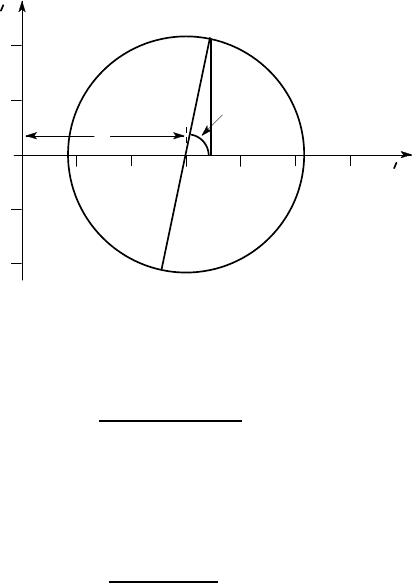
210 4 Unsymmetrical Bending

−I

> 0 , (4.50)

which conﬁrms that the denominator in equations (4.18–4.20) can never be zero or

negative.

Example 4. 6

Sketch the Mohr’s circle of second moments for the unequal Z-section of Example

4.5 (Figure 4.17) and hence determine the principal second moments I

and the

inclination of the principal axes.

From Example 4.5, we have I

=3.467a

t, I

=2.55a

t, I

=2.2a

t. The Mohr’s

circle is found by plotting the points X (I

), Y (I

,−I

) and then sketching the

circle through these points as diameter, as shown in Figure 4.22.

-1

-2

X (3.467, 2.2)

Y (2.55, -2.2)

2θ

Figure 4.22: Mohr’s circle for the unequal Z-section of Figure 4.17

The centre of the circle is deﬁned by the value

c =

(3.467 + 2.55)a

= 3.008a

and the distance CN is

CN = 3.467a

t −3.008a

t = 0.459a

t .

The radius R is therefore

R =



0.459

+ 2.2



t = 2.247a

t .

It follows that the principal second moments are

= 3.008a

t + 2.247a

t = 5.255a

= 3.008a

t −2.247a

t = 0.761a

t .

4.4 Further properties of second moments 211

The inclination of the principal axes is deﬁned by the angle

where

tan(2

) =

2.2

0.459

= 4.793 ,

giving

= 78.2

;

= 39.1

Rotation in the Mohr’s circle is in the same direction as that in the diagram of

the beam section.

To get from the point X to the point 1, we need to rotate around

the circle clockwise by 78.2

and hence the stiff axis 1 can be found by rotating the

x-axis clockwise thorugh 39.1

, as shown in Figure 4.23. The ﬂexible axis 2 is at

right angles to the stiff axis and hence is inclined at 39.1

clockwise from the y-axis

or 50.9

anticlockwise from the x-axis as shown.

A B

stiff

flexible

50.9

39.1

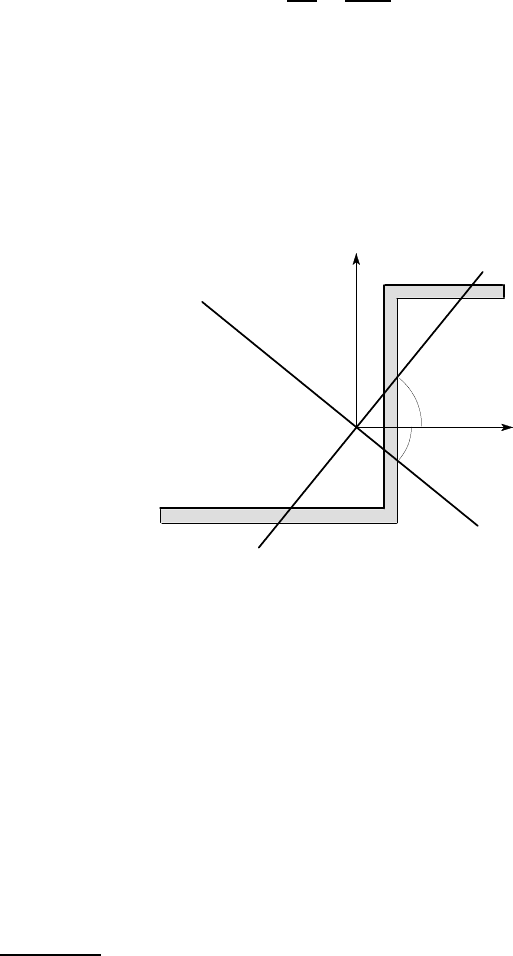
Figure 4.23: Principal axes for the unequal Z-section of Figure 4.17

Mohr’s circle of zero radius

An important class of beams includes all those whose cross sections deﬁne a Mohr’s

circle of radius R = 0. In this case, the circle reduces to a point on the I

axis and it

follows that

(i) the product inertia I

′

= 0 for all

(ii) I

′

is independent of

A beam of this class will therefore always bend only about the axis of the resul-

tant bending moment. The neutral axis will be parallel to the axis of this moment and

the ﬂexural rigidity of the beam EI will be the same for all axes.

Clearly an axisymmetric beam such as a solid or hollow circular cylinder will

behave in this way, but there are other examples as well. For example, if any three or

This is in contrast to the case of stress tranformation and results from the sign differences

noted in connection with the relations (4.46–4.48) above.

212 4 Unsymmetrical Bending

more different axes can be found about which I

is the same, the Mohr’s circle must

reduce to a point, since a vertical line can only cut the circle in two points. This is the

case if the section repeats itself every 120

(or any other submultiple of 360

greater

than 2) as shown in Figure 4.24.

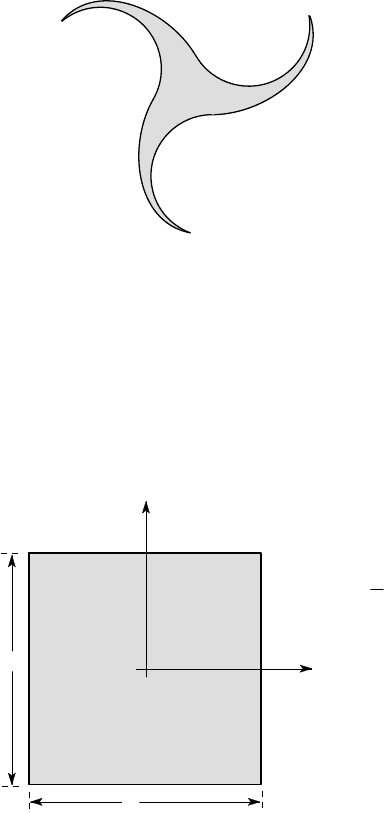
Figure 4.24: Section with three-way symmetry

It also applies to the case of a section with two planes of symmetry if the second

moments about these two axes are equal — as in the case of the square section of

Figure 4.25.

More generally, the coupling terms which cause the neutral axis to deviate from

the moment axis in unsymmetrical bending depend on the product inertia I

and are

therefore most signiﬁcant when the Mohr’s circle has a large radius (see Problem

4.29).

I = I =

Figure 4.25: The square cross section has the same second moment of area about all

centroidal axes

4.4 Further properties of second moments 213

4.4.3 Solution of unsymmetrical bending problems in principal coordinates

If the principal second moments I

and the inclination of the principal axes are

known, the bending problem is simpliﬁed by using the principal directions as co-

ordinate directions, since then there will be no coupling between the two moment

components and the problem can be solved by superposition as in § 4.1.4. It is not

generally cost effective to use this method if the principal second moments are not

already known, since the extra effort involved in determining them, added to the

greater complexity of the coordinates of the maximum stress points with inclined

Cartesian axes makes for a longer solution than that using the simultaneous equa-

tions of § 4.1.5. However, the principal second moments have been tabulated

for

commonly occurring unsymmetrical structural steel sections, so civil engineers gen-

erally prefer to solve such problems using principal coordinates.

Denoting the moments about the principal axes M

and the corresponding

radii of curvature R

respectively, equations (4.18, 4.19) reduce to

;

(4.51)

and (4.7) then gives

′

−

′

, (4.52)

where x

′

are aligned with the stiff and ﬂexible axes 1,2, respectively.

Example 4. 7

Figure 4.26 (a) shows the location of the centroid and the inclination of the principal

axes for an L5×3×1/4 unequal angle. The principal second moments are I

= 5.70

, I

=0.85 in

and the beam is loaded by a bending moment M = 2000 lb.in about

the x-axis as shown. Find the maximum tensile and compressive stresses in the sec-

tion.

We ﬁrst resolve the moment into components about the principal axes, obtaining

= M cos(37.2

) = 1593 lb.in ; M

= −M sin(37.2

) = −1209 lb.in ,

with the directions as deﬁned in Figure 4.26 (b).

These tables generally include the values of I

and the inclination of the principal

axes, but do not include the product inertia I

. In this case the only practical option is

to solve the problem in principal coordinates. However, if I

is also known, the author’s

personal opinion is that the method of §4.1.5 remains more efﬁcient because the coordinates

of the maximum stress points are then more easily determined.

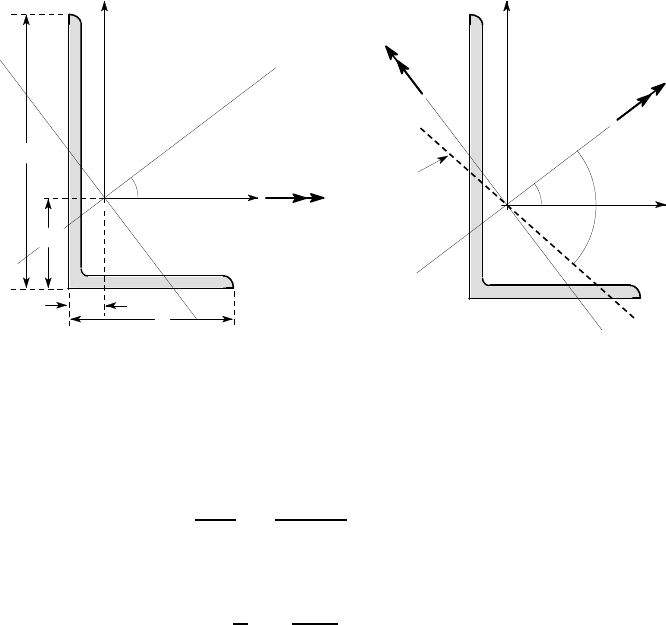
214 4 Unsymmetrical Bending

0.657

2000 lb.in

1.66

37.2

neutral

axis

78.9

all dimensions in inches

(a) (b)

Figure 4.26

The stress distribution is then given by equation (4.52) as

1593

5.70

′

−

(−1209)

0.85

′

= 279.5y

′

+ 1422x

′

(in psi if x

′

are in inches) and hence the neutral axis is deﬁned by the equation

′

= −

1422

279.5

= −5.089 .

This deﬁnes a line inclined at an angle

= tan

−1

5.089 = 78.9

clockwise from the x

′

-axis, as shown in Figure 4.26 (b).

The maximum tensile and compressive stresses will occur at the points A,B,

which are the furthest from the neutral axis. In Cartesian coordinates Oxy, the points

A,B are deﬁned by

= −0.657 in ; y

= 5 −1.66 = 3.34 in

= −0.657 in ; y

= −1.66 in.

Hence, using (4.40, 4.41), the coordinates in terms of principal axes are

′

= −0.657 cos(37.2

) + 3.34sin(37.2

) = 1.50 in

′

= 3.34 cos(37.2

) −(−0.657)sin(37.2

) = 3.06 in

′

= −0.657 cos(37.2

) −1.66sin(37.2

) = −1.53 in