Барилович В.А. Основы термогазодинамики двухфазных потоков и их численное решение
Подождите немного. Документ загружается.

140
()
v
xr
xr
nDj
x
w
w
rr
wr
rx
w
r
w
r
w
2
кпк
)(111
π
ϕ
ρ
ρ
ϕ
ρρ
ϕ
ϕ
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
(13.6)
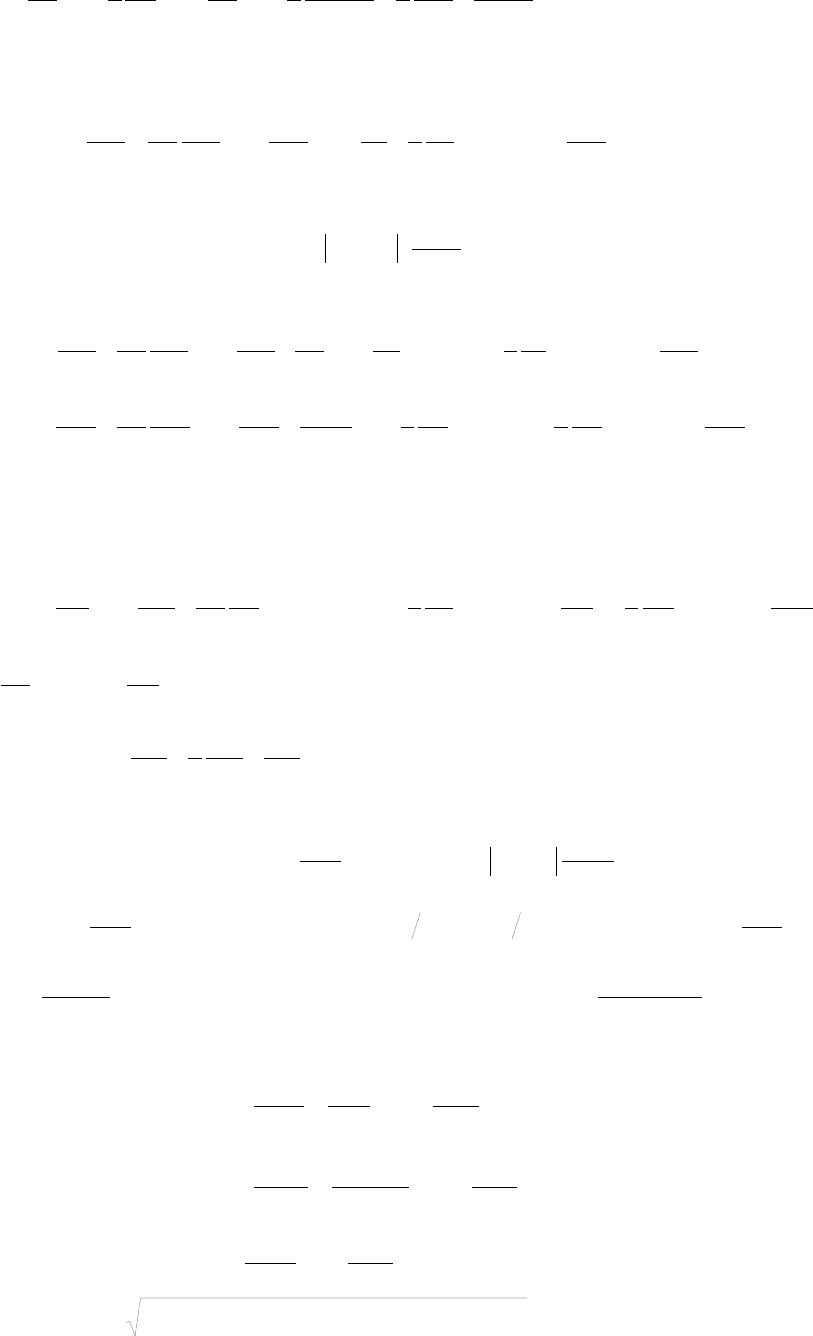
Уравнение движения газового потока с учетом наличия капель будет
иметь вид:
()
2
кпкк.xк.сопр.тб
)(
1
DjnwwF
r
w
r
rrx
p
x
w
w
w
r
w
r
w
w
vxx
xx
x
xx
r
πμμ
ϕ
ρ
ϕ
−
−−−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
+
∂
∂
+
∂
∂
−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
+
∂
∂
+
∂
∂
(13.7)
где
8
)(
2
к
кпк. ксопр
D
wwwwncF
x
xxvxx
π
ρ
−−= - проекция силы сопротивления
капельного потока на ось
x.
2
кктбксопр
2
)()(
1
Dnww
r
w
r
rr
F
r
p
r
w
x
w
w
w
r
w
r
w
w
vrr
r
r
r
x
rr
r
πμμ
ϕ
ρ
ϕϕ
−−
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
∂
∂
+−
∂
∂
−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
∂
∂
+
∂
∂
+
∂
∂
2
кктбксопр
)()(
11
Dnww
r
w
r
F
p
rr
ww
x
w
w
w
r
w
r
w
w
v
r
xr
π
ϕ
μμ
ϕϕϕ
ρ
ϕϕ
ϕ
ϕ
ϕϕϕϕϕ
−−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
+
∂
∂
+−
∂
∂
−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
∂
∂
+
∂
∂
+
∂
∂
В приближении пограничного слоя, когда
xr
ww
<
<
, а x>>r производные
от радиальной скорости
r
w
равны нулю.
Уравнение энергии представим в виде
),()()(
)(
1
)(
1
к
2
кпкк
2
кксопртб
тбтб
∗∗
−
∗∗∗
−+−+⋅+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
+
∂
∂
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
+
∂
∂
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
+
∂
∂
+⋅=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
+
∂
∂
+
∂
∂
iiDnjTTDnwF
x
T
x
r
T
rr
T
r
rr
pgradw
i
r
w
r
i
w
x
i
w
vv
rx
ππαλλ
ϕ
λλ
ϕ
λλ
ϕ
ρ
ϕ
r
r
r
где
x
pp
rr
p
pgrad
∂
∂
+
∂
∂
+
∂
∂
=
ϕ
1
. (13.8)
Для капли можно написать:
8
)(
2
к
кк
к
кк
D
wwwwc
dx
wd
wG
x
π
ρ
rrrr
r
r
−−=
, (13.9)
где
−=
к
3
к
к
6
ρ
π
D
G
масса капли;
32,0Re4,4Re24
5,0
++=
ΚΚx
c
или
к
Re
24
=
x
c (0≤ Re
к
≤1),
667,0
к
Re
24
=
x
c
( 1≤ Re
к
≤390), с
x
=0,45
( Re
к
>390),
μ
ρ
котн
к
Re
Dw
Δ
=
.
В координатной форме будем иметь:
()
()
()
,
8
,
8
,
8
отн
2
отн
2
отн
2
2
www
D
c
d
dw
G
www
D
c
r
ww
d
dw
G
www
D
c
r
w
d
dw
G
xxx
x
x
r
rrx
r
Δ−=
Δ−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
Δ−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
Κ
Κ
Κ
Κ
Κ
Κ
ΚΚΚ
Κ
Κ
Κ
Κ
Κ
Κ
ρ
π
τ
ρ
π
τ
ρ
π
τ
ϕϕ
ϕϕ
ϕ
где
()
()
()
222
отн xxrr
wwwwwww
ΚΚΚ
−+−+−=Δ
ϕϕ
- относительная скорость.
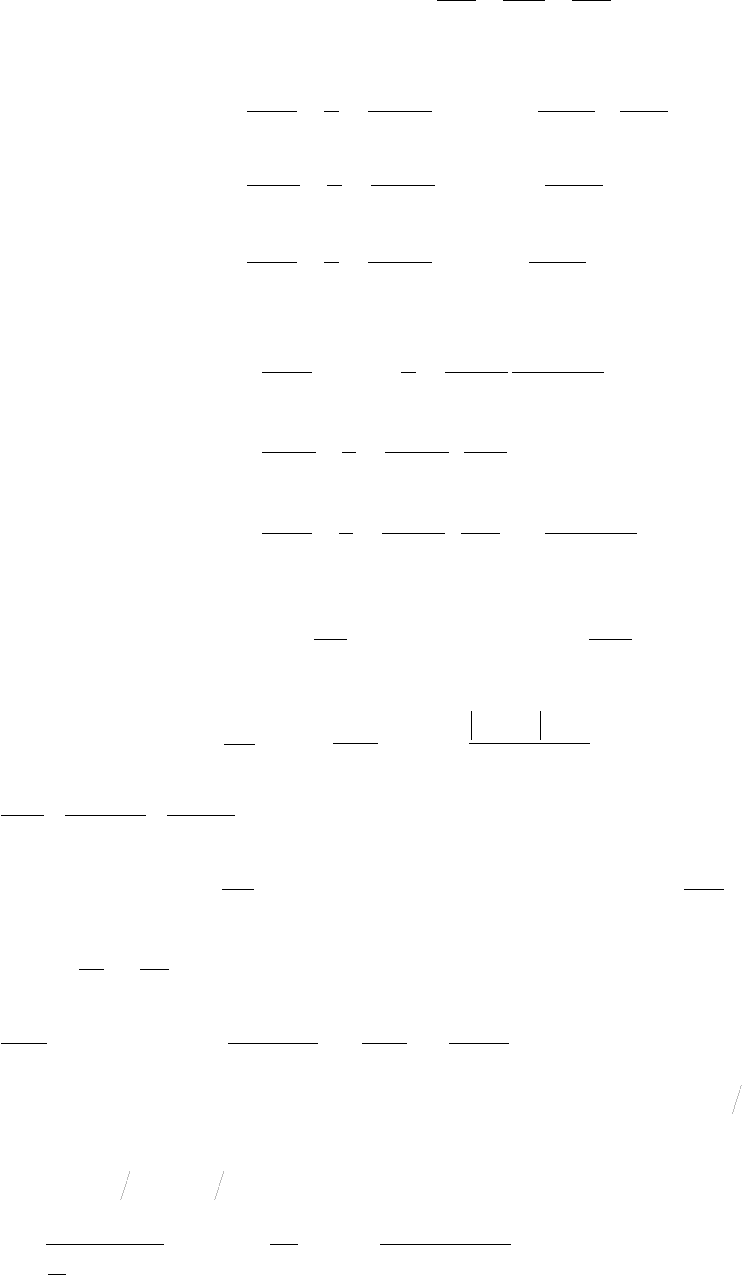
141
С учетом уравнения линии тока
xr
w
dz
w
rd
w
dr
ΚΚΚ
==
ϕ
ϕ
преобразуем уравнения
движения к виду:
()
()
()
.
4
3
,
4
3
,
4
3
отн
отн
2
отн
ϕ
ϕ
ϕϕ
ϕ
ϕ
ρ
ρ
ρ
ρ
ϕ
ρ
ρ
Κ
Κ
ΚΚ
Κ
Κ
Κ
Κ
ΚΚ
Κ
Κ
Κ
Κ
Κ
ΚΚ
Κ
Δ
−=
−
Δ
−=
+
Δ
−=
w
w
cc
D
c
dx
dw
w
w
w
ww
D
r
c
d
dw
rw
w
w
w
ww
D
c
dr
dw
xxx
x
rx
rr
rrx
r
Записывая уравнения в виде производных по
ϕ
, получим:
.1
4
3
,1
4
3
,
4
3
отн
отн
отн
ϕ
ϕ
ϕϕ
ϕ
ϕ
ρ
ρ
ϕ
ρ
ρ
ϕ
ρ
ρ
ϕ
Κ
Κ
Κ
Π
ΚΚ
Κ
Κ
Κ
Π
ΚΚ
Κ
Κ
Κ
ΚΚ
Κ
Κ
Δ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
−Δ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
Δ
−=
w
ww
w
w
D
r
c
d
dw
ww
w
w
D
r
c
d
dw
w
ww
D
r
cw
d
dw
x
x
x
x
x
rx
r
x
r
Уравнение теплового баланса для испаряющейся капли имеет вид:
dx
dG
wrTTD
dx
di
wG
к
к
rr
~
)(
к
2
к
к
кк
+−−=
πα
, (13.10)
где
23
10636,12453
~
ttr
−
⋅−−= , ( Ct 180...100= ) - удельная теплота парообразования;
()
к
5.0
к
33,0
RePr6,02
D
λ
α
+=
;
λ
μ
p
c
~
Pr =
;
μ
ρ
~
Re
кк
к
Dww
r
r
−
=
;
()
)()(
пкп
к
2
к
к
2
кпкк
TT
w
D
w
Dj
dx
dG
ρρ
βππ
−==
−
;
))()((
пкппк
TTj
ρ
ρ
β
−
=
−
;
()
к
5.033,0
~
Re6,02
D
D
Sc
к
+=
β
- коэффициент массопереноса;
D
Sc
~
~
ρ
μ
=
;
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
p
p
T
T
DD
n
0
0
0
~~
коэффициент диффузии;
−
п
ρ
плотность водяного пара.
ΚΚΚ
Π−ΚΚ
Π−ΚΚ
Π
==
wD
jG
FnjD
dx
Gd
Cv
ρ
π
&&
6
2
,
ΚΚ
Π−ΚΚ
−=
w
j
dx
dD
ρ
2
.
ΠΓ
+= GGG
&&&
0
,
constGGGG =++=
ΓΚΠ 000СМ
&&&&
,
кп
GdGd
&&
−= ,
(
)
ΠΓΓΠΓΠ
+=
μμμμμ
GGG
&&&
,
(
)
ΠΠΠ
=
μμ
GpGp
&&
/
- парциальное давление пара в газопаровой смеси,
(
)
GGGRR
&&&
/
00 ΠΠΓΓ
+=
μμ
,
(
)
GGcGcc
ppp
&&&
/
ΠΠΓΓ
+=
,
(
)
ΚΠ
=
Tfp
S
.
()
пг
1
uRR
p
T
u
+
+
=
ρ
, где
г
п
G
G
u
&
&
=
;
p
pp
c
uTcTc
T
кпгг
+
=
.
2966
1003,01005,0102,17
~
tt
−−−
Γ
⋅−⋅+⋅=
μ
;
2853
102908,4104189,8108,23 tt
−−−
Γ
⋅−⋅+⋅=
λ
;

142
[
324"
10]102904,22501 ⋅⋅−+=
−
Π
tti
;
23
10695,21475,09,999 tt
−
Κ
⋅−−=
ρ
;
μ
ρ
~
/Re
C
Dw=
;
25,0
Re079,0=
f
c
;
2/
2
wc
fW
ρτ
=
;
()
(
)
ρρ
wGwGF
C
&&
+=
ΚΚΚ
;
π
CC
FD 4=
;
24
п
107314,6129299,07962,6 tt
−
⋅+−=
ρ
;
22
к
1098,109,34331 ttc
p
−
⋅+−=
;
))ln(48776,11/541,782101028003,086568,82exp(10)(
6
TTTTp
s
−−+=
;
32
п
10)0000736,00132,0719,2( ttc
p
+−=
;
9,461
пп
−
=
pv
сc
.
323'
п
10)103125,1935,3475,12( tti
−
⋅++=
;
323''
п
10)1088,4636,21,2461( tti
−
⋅−+=
;
323
10)1026,6283,17,2447(
~
ttr
−
⋅−−= ;
2253''
п
10)1002,31069,2801,1(
−−−
⋅+⋅+= tt
λ
;
623'
10)1022,9227,4613(
~
−−
⋅+−= tt
μ
;
6252"
10)1021042,335,8(
~
−−−
⋅+⋅+= tt
μ
;
253''
104,24,428,1Pr tte
−−
⋅+−=
;
))ln(5089,24(
8222,4842
)(
p
pTs
−
=
;
Для давлений
Па10)1...1,0(
5
⋅=p :
))ln(1592,25(
1472,5085
)(
p
pTs
−
=
.
При решении обратной задачи можно считать, что закон изменения
статического давления вдоль продольной оси сопла подчиняется
зависимости:
11
2
cp
0
0
+
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=
l
x
p
p
p
p
, тогда
(
)
()
2
2
cp0
2
cp0
11/
1/2
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛
−
−
−=
l
x
ppl
xppp
dx
dp
o
.
При решении прямой задачи необходимо задать геометрию сопла.
Будем считать, что сопло Лаваля состоит из двух усеченных прямых конусов
и цилиндрического горла. В этом случае геометрия сопла описывается
уравнениями:
кон.min00
/)( zxDDDD
ccc
−−= , если
кон.
zx
≤
;
min
DD
c
=
, если )(и
minконкон
zzxzx
+
≤≥ ;
дивminконminсрезmin
/))(()( zzzxDDDD
c
+−⋅−+=
, если )(
minкон
zzx
+
〉 ;
4/
2
cc
DF
π
=
.
конmin0конmin00
/2/)()/)((/ zDDzxDDDdxdF
cccc
−
⋅
⋅−−−=
π
, если
кон.
zx
≤
;
0/ =dxdF
c
, если )(и
minконкон
zzxzx
+
≤≥ ;
)2/()()/))(()((/
дивminсрездивminконminсрезmin
zDDzzzxDDDdxdF
c
−
⋅
+
−⋅−+=
π
,
если
)(
minкон
zzx +〉 .
Используя разложение искомых функций в ряд Тейлора (математический
подход к решению задачи) можно записать уравнения (13.6)-(13.10) в
конечно-разностном виде, получив систему алгебраических уравнений с
погрешностью аппроксимации, которые можно решить при заданных
граничных условиях, например, методом Гаусса-Зайделя.
Покажем, как в этом случае получают конечно-разностную
аппроксимацию производных первого и
второго порядка.
Разложим функцию
u(x,y) в ряд Тейлора разностью “вперед “

143
!
)(
....
!2
)(
),(),(
2
0
2
2
00000
n
x
x
u
x
x
u
x
x
u
yxuyxxu
n
n
n
Δ
∂
∂
+
Δ
∂
∂
+Δ
∂
∂
+=Δ+
ξ
, (a)
откуда получим
....
2
),(),(
2
2
0000
0,0
−
Δ
∂
∂
−
Δ
−Δ+
=
∂
∂ x
x
u
x
yxuyxx
x
u
yx
или
)(
,,1
,
xO
x
uu
x
u
jiji
ji
Δ+
Δ
−
=
∂
∂
+
, где )( xO
Δ
- погрешность аппроксимации.
Для разности “назад” можно написать:
....
!2
)(
),(),(
2
0
2
2
00000
−
Δ
∂
∂
+Δ
∂
∂
−=Δ−
x
x
u
x
x
u
yxuyxxu
(b)
Из (b) найдем
)(
,1,
,
xO
x
uu
x
u
jiji
ji
Δ+
Δ
−
=
∂
∂
−
. Вычитая (b) из (а), получим
аппроксимацию первой производной центральными разностями
−Δ+ ),(
00
yxxu
2
00
)(2),( xO
x
u
xyxxu Δ+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
Δ=Δ− или
2
,1,1
)(
2
,
xO
x
uu
x
u
jiji
ji
Δ+
Δ
−
=
∂
∂
−+
.
Складывая (a) и (b), определим конечно-разностную аппроксимацию
производной второго порядка
2
2
2
2
000000
)(
2
)(
2),(2),(),( xO
x
x
u
yxuyxxuyxxu Δ+
Δ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
=−Δ−+Δ+
, откуда в общем
виде можно написать:
2
2
,,1,1
,
2
2
)(
)(
2
,
xO
x
uuu
x
u
jijiji
ji
Δ+
Δ
−+
=
∂
∂
−+
.
Однако в такой постановке делается предположение, что при этом
выполняются законы сохранения. Поэтому наибольшее распространение
получил метод контрольного объема (МКО) [26], который является
консервативным (в каждом КО выполняются законы сохранения). В этом
случае уравнения записываются в дивергентном виде и интегральной форме.
Рассмотрим паро-капельный поток.
Выделим в цилиндрической системе координат
элементарный объем и
получим необходимые геометрические соотношения (см. рис.13.1). Площадь
кольца
)(2
snpew
rrrSS −=Δ=Δ
π
, где
2/)(
snp
rrr
+
=
- радиус полюса. Объем кольца
zSV
w
ΔΔ=Δ
. Боковые поверхности цилиндров высотой
.2)(2,2)(2: zrzzrSzrzzrSz
swessnwenn
Δ
=
−
=
Δ
Δ=−=ΔΔ
π
π
π
π
Рис. 13.1
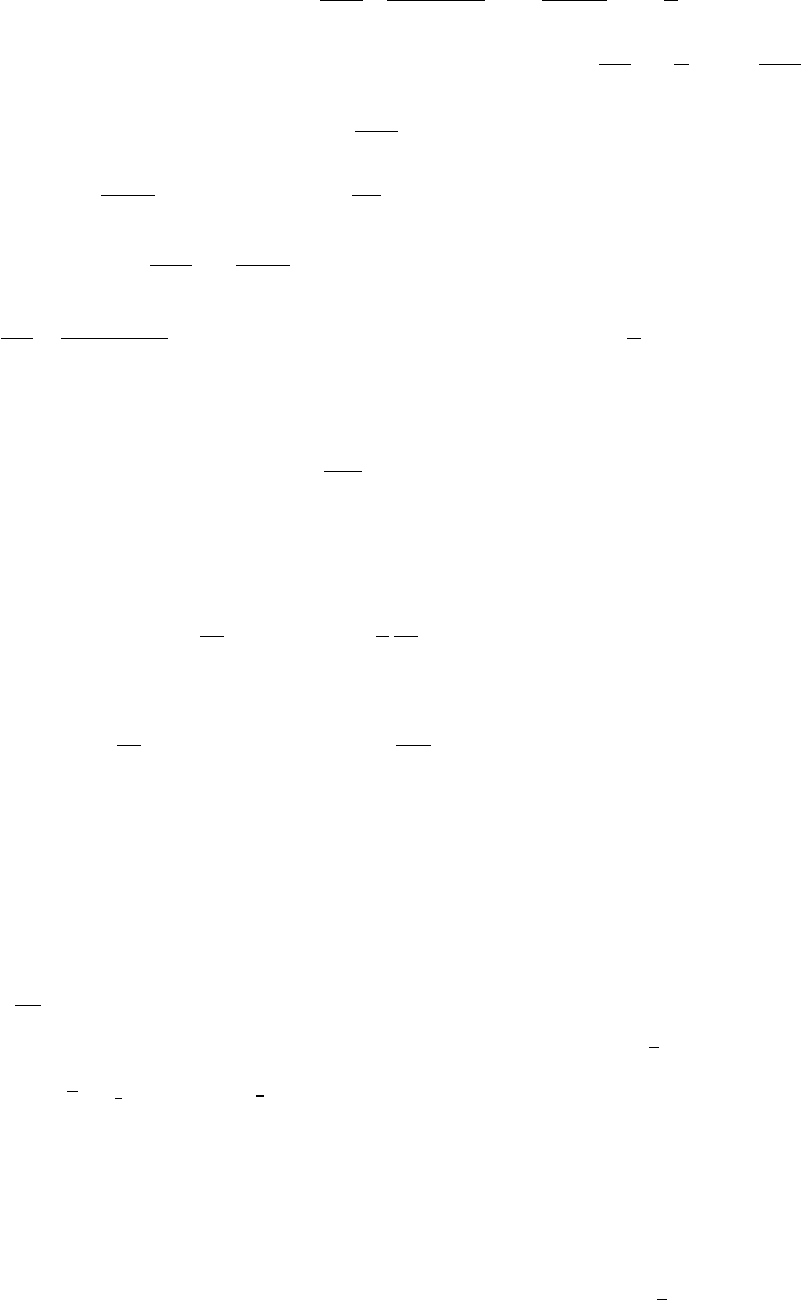
144
Введем объемные доли пара
α
и капель
β
и найдем связь между
α
и
диаметром капли
.
6
1
1
6
1
3
к
3
кккп
Dn
V
Dn
V
VV
V
V
v
π
π
α
−=
Δ
−=
Δ
Δ−Δ
=
Δ
Δ
= Возьмем
производную от
α
по направлению
l
:
dl
dD
nD
dl
d
v
к
2
к
2
1
π
α
−=
(c), но
τπ
dDjdG
2
кпкк
−
−=
(d), где
к
3
к
к
6
ρ
π
D
G =
. После дифференцирования (d) получим
τ
ρ
d
j
dD
к
пк
к
2
−
−=
. Так как
τ
d
dl
w =
к
, то, подставляя
τ
d в предыдущую формулу,
найдем, что
кк
пкк
2
w
j
dl
dD
ρ
−
−=
(e). Теперь (c) с учетом (e) можно переписать в виде
кк
2
кпк
w
nDj
dl
d
v
ρ
π
α
−
= (k). Объемная доля капель
.
6
1
1
3
к v
nD
παβ
=−=
Для потока пара, несущего испаряющиеся капли, уравнение сплошности
запишем в виде:
v
nDjw
2
кпкп
п
)(div
παρ
τ
ρ
−
=+
∂
∂
r
, (13.11)
где
)/(lim
пп0п
VG
V
ΔΔ=
→Δ
ρ
- истинная плотность пара.
При стационарном режиме течения в цилиндрической системе координат и
интегральной форме применительно к КО (13.11) преобразуется к виду
() ()
∫∫∫
Δ
−
ΔΔ
=
∂
∂
+
∂
∂
V
vr
V
z
V
dVnDjdVwr
rr
dVw
z
2
кпк
пп
1
πρααρ
. (13.12)
Перепишем (13.12) в иной форме (см. рис.13.1)
() ()
ϕπϕραϕαρ
πππ
rdrdzdnDjrdrdzdwr
rr
rdrdzdw
z
v
r
rz
r
r
rz
z
r
rz
n
s
n
s
n
s
∫∫∫∫∫∫∫∫∫
−
ΔΔΔ
=
∂
+
∂
∂
2
кпк
2
0
п
2
0
п
2
0
1
.
(13.13)
Для первого слагаемого в левой части уравнения после интегрирования
можно написать:
[][]
(){}
22
)()()()(2
snwzez
r
r
wzez
rrwwrdrww
n
s
−−=
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
−
∫
αραρπαραρπ
, для
второго получим:
[]
srnr
wrwrz )()(2
ρ
α
ρ
α
π
−
Δ , используя очевидное равенство
fdl
l
f
l
=
∂
∂
∫
. В окончательном виде будем иметь:
[]
(){}
[
]
(
)
2222
)()(2)()(
snPsrnrsnwzez
rrJzwrwrzrrww −Δ=−Δ+−−
&
πραραπαραρπ
, (13.14)
где
vP
nDjJ
2
кпк
π
−
=
&
; j - осредненная плотность потока массы пара от
испаряющейся капли в КО. Полученное уравнение относится к КО,
находящемуся внутри потока и не прилежащему к границе, где задаются
условия на входе, выходе и стенке канала.
Для КО, находящегося в центре канала после интегрирования (13.13)
получим
[
]
{}
[
]
22
)(2)()(
nPnrnwzez
rJzwrzrww
&
Δ=Δ+−
πραπαραρπ
. (13.14а)
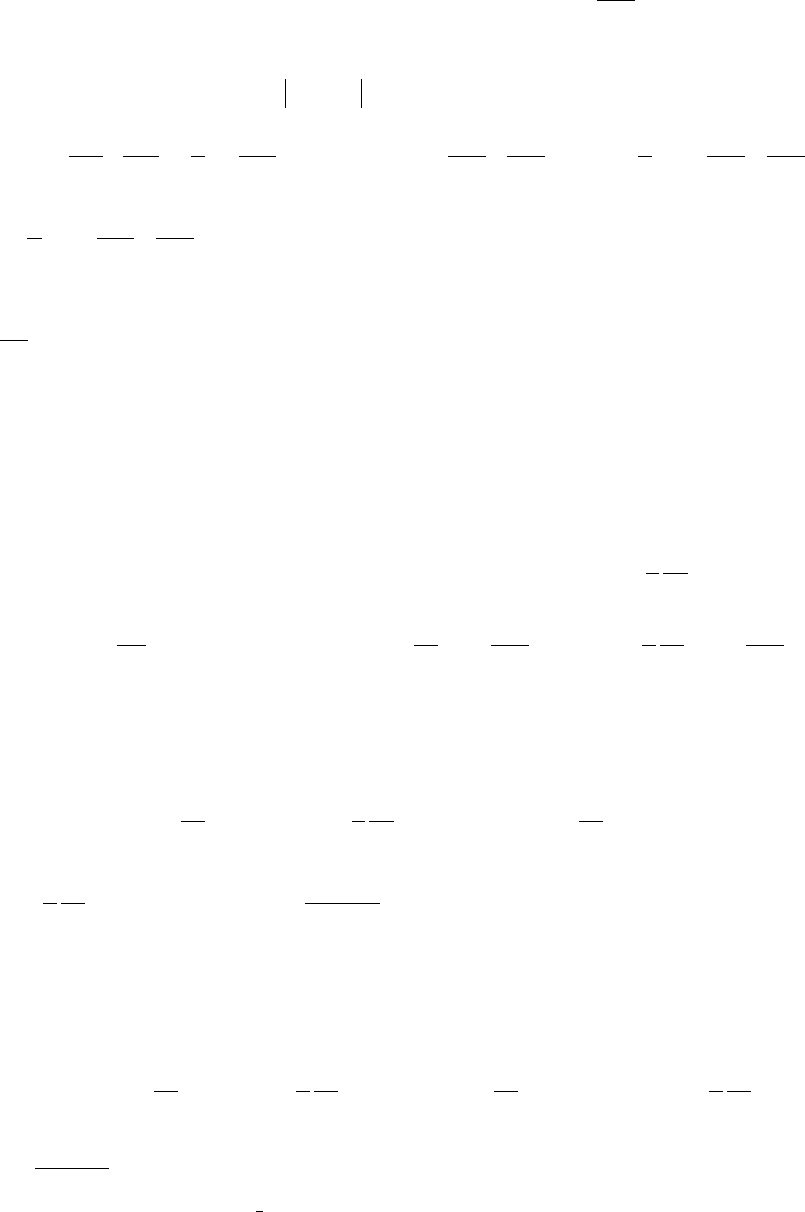
145
Преобразуем (12.21) в дивергентную форму. Для стационарного режима
уравнение (12.21) примет вид:
(
)
(
)
gwwJFww
пкппкп-ксопр
0
ппппп
div
ρααρ
+−−+Π∇=
−
v
v
&
r
r
r
. (13.15)
Умножим уравнение сплошности (13.11) на
п
w
r
при 0
п
=
∂
∂
τ
ρ
и сложим с (13.15)
(
)
gwJFwwwwww
пкпкпк.сопр
0
ппппппппп
)(divdiv)(Div
αρααραραρ
++−Π∇=+=
−−
r
&
r
r
r
r
r
r
r
, (13.16)
где
8/)(
кпкпп
2
кп-ксопр vx
nwwwwDсF −−=
r
r
r
ρπ
;
v
nDjJ
2
кп-кп-к
π
=
&
;
jijiji
p
τδ
+−=Π=Π
0
п
;
n
k
k
ji
i
j
j
i
ji
x
u
x
u
x
u
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
∂
∂
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
+
∂
∂
=
δμτ
3
2
п
;
n
rz
zrrz
z
w
r
w
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
∂
∂
==
п
μττ
;
n
rz
zz
r
w
z
w
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
∂
∂
= 2
3
2
п
μτ
;
n
zr
rr
z
w
r
w
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
−
∂
∂
= 2
3
2
п
μτ
. В общем случае при нестационарном режиме течения и
интегральной форме можно написать:
() ( )
(
)
dVgdVFdVwJdVdVwwdVw
VVVVVV
∫∫∫∫∫∫
ΔΔ
−
Δ
−
ΔΔΔ
+−+Π=+
∂
∂
ппксопркпк
п
0
пп
divDiv
αρααραρ
τ
r
r
&
v
rr
Запись уравнения движения в конечно- разностном виде представляет
значительную сложность из-за необходимости написания большого числа
алгебраических уравнений. Поэтому, получив представление о написании
уравнения, упростим его сохранив основные воздействия на поток. Для
стационарного режима получим:
()
()
∫∫∫∫∫
ΔΔ
−
Δ
−
ΔΔ
∂
∂
+−+−=
VVVVV
dVr
rr
dVFdVwJdVpdVww
п
тр.пксопркпкп
п
1
)(gradDiv
ταααρ
r
r
r
&
v
r
, (13.17)
где
r
w
z
∂
∂
=
r
r
μτ
.тр
. Здесь считаем, что
∫∫
ΔΔ
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
<<
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
V
z
V
z
dV
r
w
r
rr
dV
z
w
z
пп
1
μαμα
.
Проинтегрируем уравнение (13.17) в цилиндрической системе координат.
Для левой части уравнения можно написать (подстрочный индекс “п”-пар
опускаем):
()
()
() ()()
[]
()()
[]
).(2
)(
2
)(
2
1
)(
1
)(Div
22
222
2
0
2
2
0
22
wes
s
rn
n
r
w
z
e
zsn
ns
r
z
r
r
z
z
r
r
r
V
z
VV
zzrwrw
wwrr
rr
rdrdzdwr
rr
rdrdzdw
z
dVrw
rr
dVw
z
dVww
n
s
n
s
−−+
+−
⎥
⎦
⎤
⎢
⎣
⎡
−
+
=
∂
∂
+
+
∂
∂
=
∂
∂
+
∂
∂
=
∫∫∫
∫∫∫∫∫∫
Δ
ΔΔΔΔ
αραρπ
αραρπϕρα
ϕαραραραρ
π
π
v
r
Для слагаемых в правой части уравнения соответственно будем иметь:
() () () ()
()()
[]
() ()
[]
),(2)(
2
)(
2
11
)(grad
2
0
2
0
wes
s
n
nwe
sn
ns
z
r
rz
r
rVVV
zzrprppprr
rr
rdrdzdrp
rr
rdrdzdp
z
dVrp
rr
dVp
z
dVp
n
s
n
s
−−+−
⎥
⎦
⎤
⎢
⎣
⎡
−
+
=
=
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
=
∫∫∫∫∫∫∫∫∫
ΔΔΔΔΔ
ααπααπ
ϕαϕαααα
ππ
(
)
,
к
2
кпккпккпк
VwnDjVwJdVwJ
zvz
V
Δ=Δ=
−−
Δ
−
∫
π
&
r
&
146
VnwwwwDс
nwwwwDсdVFdVF
wv
z
zx
ev
z
zxz
VV
Δ−−−
−−−==
∫∫
Δ
−−
Δ
))8/)((
)8/)((()(
кпкпп
2
к
кпкпп
2
кпксопрпксопр
ρπ
ρπ
r
(здесь считаем, что dVFdVF
r
V
z
V
)()(
пксопрпксопр
∫∫
Δ
−
Δ
−
>> ),
(
)
=
∂
∂
∫
ΔV
dVr
rr
тр
1
τα
r
() ()
[]
.)(
2
)()(
2
)(
2
22
1
zSs
P
zsnzNn
z
SP
SP
s
z
PN
PN
n
r
r
z
V
z
wr
r
z
wrr
r
z
wr
r
z
rr
ww
r
rr
ww
rzrd
r
w
r
r
zdV
r
w
r
rr
n
s
μα
π
μαμα
π
μα
π
μαμαπμαπμα
⎟
⎠
⎞
⎜
⎝
⎛
Δ
Δ
++
⎟
⎠
⎞
⎜
⎝
⎛
Δ
Δ
+
⎟
⎠
⎞
⎜
⎝
⎛
Δ
Δ
=
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
Δ=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
Δ=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
∫∫
Δ
Обозначим
()()
[]
()()
[]
),(2)(
2
)(
2
2222
wes
s
rn
n
r
w
z
e
zsn
ns
zzrwrwwwrr
rr
FKD −−+−
⎥
⎦
⎤
⎢
⎣
⎡
−
+
=
αραρπαραρπ
()()
[]
() ()
[]
),(2)(
2
)(
2
wes
s
n
nwe
sn
ns
zzrprppprr
rr
GRP −−+−
⎥
⎦
⎤
⎢
⎣
⎡
−
+
=
ααπααπ
,
к
2
кпкпк
VwnDjJ
zv
Δ=
−−
π
,))8/)(()8/)(((
кпкпп
2
ккпкпп
2
кпк
VnwwwwDсnwwwwDсF
wv
z
zxev
z
zx
Δ−−−−−=
−
ρπρπ
[]
,)(
2
)()(
2
)(
2
тр zSsPsnzNn
wr
r
z
wrr
r
z
wr
r
z
F
μα
π
μαμα
π
μα
π
⎟
⎠
⎞
⎜
⎝
⎛
Δ
Δ
++
⎟
⎠
⎞
⎜
⎝
⎛
Δ
Δ
+
⎟
⎠
⎞
⎜
⎝
⎛
Δ
Δ
=
[]
.)(
2
,)()(
2
,)(
2
ssnn
r
r
z
Krr
r
z
Hr
r
z
E
μα
π
μαμα
π
μα
π
⎟
⎠
⎞
⎜
⎝
⎛
Δ
Δ
=+
⎟
⎠
⎞
⎜
⎝
⎛
Δ
Δ
=
⎟
⎠
⎞
⎜
⎝
⎛
Δ
Δ
=
Теперь уравнение движения примет вид:
,
пкпк S
z
PN
KwHwEwFJGRPFKD +−+−+−=
−−
&
из которого определим скорость парового потока для внутреннего КО
).(
1
пкпк SN
z
P
KwEwFJGRPFKD
H
w ++−+−−=
−−
&
Запишем уравнение энергии парового потока в дивергентном
виде:
п
кпкпк
2
кпк
ппсопр.кппппппп
1
)(
)grad(div)(grad)(div)grad()(div
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
++−+
+++=+=
∗
−−
−
r
w
rw
rr
iJTTDn
wFi
c
pwwiiwiw
v
p
r
r
&
r
r
rrrr
μαπα
λα
ααραραρ
или
,
1
)(
)grad(divdiv)()(div)(div
п
кпкпк
2
кпк
ппсопр.кппппп
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
++−+
+++−=
∗
−−
−
r
w
rw
rr
iJTTDn
wFi
c
wpwpiw
v
p
r
r
&
r
r
rrr
μαπα
λα
αααρ
(13.18)
так как
abbaba graddiv)(div
r
r
r
+=
. Для однокомпонентного потока слагаемое
.0)(
пк
2
кпк
=−
−
TTDn
v
πα
Запишем (13.18) в интегральной форме

147
)19.13(.
1
)(
)grad(divdiv)()(div)(div
кпкпк
2
кпкппсопр.к
ппппп
∫∫∫∫
∫∫∫∫
ΔΔ
∗
−
Δ
−
Δ
−
ΔΔΔΔ
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
++−+
++−=
VVV
v
V
V
p
VVV
dV
r
w
rw
rr
dViJdVTTDndVwF
dVi
c
dVwpdVwpdViw
r
r
&
r
r
rrr
μαπα
λα
αααρ
Уравнение энергии парового потока (13.19) в цилиндрической системе
координат примет вид:
() ()
()
(13.20).
1
)()()(
1
1
)(
1
)(
пкпк
2
кпкпсопр.кпсопр.к
∫
∫∫∫∫
∫∫∫∫
∫∫∫∫
Δ
∗
Δ
−
Δ
−
Δ
−
Δ
−
ΔΔΔΔ
ΔΔΔΔ
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
+
++−+++
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
+
∂
∂
−
∂
∂
−
−
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
V
z
z
VV
vr
V
z
V
p
V
p
V
r
V
r
V
z
r
V
z
V
r
V
z
V
dV
r
w
rw
rr
dViJdVTTDndVwFdVwF
dV
r
i
c
r
rr
dV
z
i
cz
dVrw
rr
p
dV
z
w
p
dVrpw
rr
dVpw
z
dVirw
rr
dViw
z
μα
πα
λααλα
α
αααραρ
&
Проинтегрируем левую часть уравнения (13.20) в пределах КО, находящегося
внутри потока
() ()
()()
[]
()()
[]
).(2)(
2
)(
2
1
)(
1
)(
2
0
2
0
wes
s
rn
n
r
w
z
e
zsn
ns
r
z
r
r
z
z
r
r
r
V
z
V
zzriwriwiwiwrr
rr
rdrdzdiwr
rr
rdrdzdiw
z
dVirw
rr
dViw
z
n
s
n
s
−−+−
⎥
⎦
⎤
⎢
⎣
⎡
−
+
=
=
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
∫∫∫∫∫∫∫∫
ΔΔΔΔ
αραρπαραρπ
ϕραϕαραραρ
ππ
Рассмотрим правую часть уравнения. Для двух первых слагаемых можно
написать:
() () () ()
()()
[]
()()
[]
).(2)(
2
)(
2
11
2
0
2
0
wes
s
rn
n
r
w
z
e
zsn
ns
r
z
r
r
z
z
r
r
r
V
z
V
zzrpwrpwpwpwrr
rr
rdrdzdrpw
rr
rdrdzdpw
z
dVrpw
rr
dVpw
z
n
s
n
s
−−+−
⎥
⎦
⎤
⎢
⎣
⎡
−
+
=
=
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
∫∫∫∫∫∫∫∫
ΔΔΔΔ
ααπααπ
ϕαϕααα
ππ
Для третьего и четвертого слагаемых будем иметь:
()
() ()
() ()
.2
2
2
22
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
−
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
−
Δ−
−Δ
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
−
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−=
=
∂
∂
−
∂
∂
−
∫∫
ΔΔ
s
s
SrSPrP
s
n
n
PrPNrN
n
w
zW
P
z
w
e
zP
E
z
e
sn
r
VV
z
r
r
rwrw
pr
r
rwrw
pz
z
z
ww
p
z
ww
p
rr
dVrw
rr
p
dV
z
w
p
ααπ
ααπ
α
α
Чтобы понять суть интегрирования пятого слагаемого, проинтегрируем
подинтегральную функцию по оси
z в пределах z
Δ
КО (см. рис.13.1).
148
.
м
Вт
,
2
W
w
p
P
w
p
e
p
E
e
p
WP
w
p
PE
e
p
w
p
e
pp
e
w
i
zc
i
z
cc
i
zc
z
ii
cz
ii
cdz
i
cdz
i
c
dz
z
i
cz
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
+
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
Δ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
=
=
⎟
⎠
⎞
⎜
⎝
⎛
Δ
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
Δ
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
∫
αλ
αλαλ
αλ
αλαλαλαλαλ
Тогда для нашего случая будем иметь:
dV
z
i
cz
p
V
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
∫
Δ
αλ
= ,
2
)()(
2
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎬
⎫
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
+
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
Δ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
−+
W
w
p
P
w
p
e
p
E
e
p
snsn
i
zc
i
z
cc
i
zc
rrrr
αλ
αλαλ
αλ
π
где
ew
snsn
SS
rrrr
Δ=Δ=
−+
2
))((2
π
- площадь элементарного кольца.
Из полученного уравнения видим, что значение удельной энтальпии в
искомой ячейке
P
i зависит как от физических свойств потока на гранях
ячейки, так и значений удельной энтальпии в соседних узлах (
EW
ii , ).
Для шестого слагаемого можно написать:
.
22
2
2
2
11
2
0
S
s
p
s
P
s
p
s
n
p
n
N
n
p
n
SP
SP
s
pPN
PN
n
p
r
r
p
z
r
r
pp
V
i
cr
zr
i
c
r
c
r
r
z
i
cr
zr
rr
ii
c
r
rr
ii
c
r
z
rd
r
i
c
r
r
zrdrdzd
r
i
c
r
rr
dV
r
i
c
r
rr
n
s
n
s
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
Δ
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
Δ
−
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
Δ
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
Δ=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
∫∫∫∫∫
ΔΔ
αλπαλαλπ
αλπαλαλ
π
αλ
πϕ
αλαλ
π
Складывая пятое и шестое слагаемые, получим:
.
2
22
1
S
s
p
s
N
n
p
n
P
s
p
s
n
p
n
w
p
e
p
W
w
p
E
e
pp
V
p
V
i
cr
zr
i
cr
zr
i
c
r
c
r
r
z
zczc
S
i
zc
i
zc
SdV
r
i
c
r
rr
dV
z
i
cz
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
Δ
+
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
Δ
+
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
Δ
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
Δ−
−
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
Δ=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
∫∫
ΔΔ
αλπ
αλπαλαλπαλαλ
αλαλλααλ
Считая, что
dVwFdVwF
r
V
z
V
)()(
пксопр.пксопр.
∫∫
Δ
−
Δ
−
>> , можно написать:
.))8/)((
)8/)((()(
пкпкпп
2
к
пкпкпп
2
кпсопр.кппсопр.к
VwnwwwwDс
wnwwwwDсdVwFdVwF
wzv
z
zx
ezv
z
zxz
VV
Δ−−−
−−−==
∫∫
Δ
−−
Δ
ρπ
ρπ
r
r
Для потока теплоты от капель несущему потоку будем иметь:
149
VTTDndVTTDn
v
V
v
Δ−=−
−
Δ
−
∫
)()(
пк
2
кпкпк
2
кпк
παπα
,
где
пк−
α
- средний коэффициент теплоотдачи от капель к пару.
Для потока энтальпии пара от капель можно написать:
(
)
ViJdViJ
V
Δ=
∗
−
∗
Δ
−
∫
кпккпк
&&
, где
v
nDjJ
2
кпкпк
π
−−
=
&
.
Для последнего слагаемого после интегрирования будем иметь:
() ()
.2
2
11
2
0
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
Δ=
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
Δ=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
∫∫∫∫∫
ΔΔ
SP
SP
s
z
PN
PN
n
z
r
r
z
z
z
r
r
z
z
z
z
V
rr
ww
rw
rr
ww
rwz
rd
r
w
rw
r
zrdrdzd
r
w
rw
rr
dV
r
w
rw
rr
n
s
n
s
μαμαπ
μαπϕμαμα
π
Для учета градиента касательных напряжений вдоль продольной оси
z необходимо в уравнение энергии добавить слагаемое
() ()
,)(
22
2
0
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
−=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
∫∫∫∫
ΔΔ
z
WP
WP
w
z
z
PE
PE
e
zsn
z
r
r
z
z
z
z
V
zz
ww
w
zz
ww
wrr
rdrdzd
z
w
w
z
dV
z
w
w
z
n
s
αμαμπ
ϕαμαμ
π
вклад которого существенно меньше предыдущего.
Рассматривая течение внутри пограничного слоя, слагаемые
zrwrp
zr
∂
∂∂∂∂∂ /,/,/
τ
можно положить равными нулю.
Введем обозначения для слагаемых в уравнении энергии.
()()
[]
()()
[]
),(2)(
2
)(
2
wes
s
rn
n
r
w
z
e
zsn
ns
zzriwriwiwiwrr
rr
FI −−+−
⎥
⎦
⎤
⎢
⎣
⎡
−
+
=
αραρπαραρπ
()()
[]
()()
[]
),(2)(
2
)(
21
wes
s
rn
n
r
w
z
e
zsn
ns
zzrpwrpwpwpwrr
rr
NP −−+−
⎥
⎦
⎤
⎢
⎣
⎡
−
+
=
ααπααπ
() ()
() ()
.2
2
22
22
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
Δ
−
−
⎟
⎠
⎞
⎜
⎝
⎛
Δ
−
Δ−
−Δ
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
Δ
−
−
⎟
⎠
⎞
⎜
⎝
⎛
Δ
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−=
s
s
SrSPrP
s
n
n
PrPNrN
n
w
zW
P
z
w
z
e
zP
E
z
e
z
sn
r
r
rwrw
pr
r
rwrw
pz
z
z
ww
p
z
ww
p
rr
NP
ααπ
ααπ
Для пятого и шестого слагаемых
,
)(
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
Δ=
− W
w
p
E
e
p
WE
i
zc
i
zc
SAi
αλαλ
P
s
p
s
n
p
n
w
p
e
p
P
i
c
r
c
r
r
z
zczc
SBi
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
Δ
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
Δ=
αλαλπαλαλ
2
;
.
22
S
s
p
s
N
n
p
n
SN
i
cr
zr
i
cr
zr
DiCi
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
Δ
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
Δ
=+
αλ
π
αλ
π
Мощность сопротивления капельного потока, мощность теплового потока
от капель, мощность потока энтальпии пара от испаряющихся капель и
