Bayer R.G. Mechanical Wear Fundamentals and Testing, Revised and Expanded

Подождите немного. Документ загружается.

chip formation. Repeated-cycle deformation wear results from the accumulation of plastic

strain associated with the stress cycle, culminating in progressive plastic deformation,

crack formation, and crack propagation.

This consideration of hysteretic friction points out a signiﬁcant aspect of friction,

namely that it results in the dissipation of energy. The energy associ ated with friction is

dissipated in two general ways. The vast majority of the energy is dissipated as heat

(3–5). A much smaller amount is associated with material loss or deformation, that is,

wear. Most estimates indicate that well over 90% of the energy dissipated in friction goes

in the form of heat energy.

Models have been proposed for these friction mechanisms but are typically limited

in applicability. Generally, all of the models indicate a more complex situation than indi-

cated by the postulations of da Vinci and Amontons (ca. 1500 and 1700, respectively)

which frequently are used in engineering. These statements, commonly referred to as

Amontons’ Laws of Friction, may be summarized as: (1) the friction force is propor-

tional to the normal load, (2) the friction force is independent of the apparent area of

contact. The current models, as well as experimental data, indicate that these conclu-

sions should be viewed as approximations with a limited range of applicability. This

view can be illustrated by the consideration of some simple models for friction force

and the coefﬁcient of friction and some examples of observed behavior. For simplicity,

only dry or unlubricated surfaces will be considered at this point. Friction behavior

under lubricated conditions will be discussed in the section on lubrication. A model used

for paper can be used as a way of illustrating these general models (6).

For adhesion, the general concept is that the F

is given by

¼ sA

ð5:4Þ

where s is the shear strength of the junctions, and A

is the real area of contact (7). s is a

property of the material system at the interface and is inﬂuenced by the same parameters

as discussed for adhesive wear (e.g., oxides, cleanliness of the surface, solubility, material

strength properties). As was discussed in the sections on wear, A

can be affected by mate-

rial properties, asperity distribution, and contact geometry. For example, in the case of a

sphere pressed against a plane, a general relationship for A

is of the following form:

¼ CR

ð5:5Þ

where C is a material parameter, R is the radius of the sphere, and P is the normal load

(8,9). The exponents, n and m, are positive and depend on both the nature of the stress

system at the junctions and the asperity distribution. For plastic deformation, n ¼ 0

and m ¼ 1. For elastic deformation, n > 0 and m is between 0 and 1 for relatively simple

asperity distributions but can be greater than 1 for some complex asperity distributions.

The expression for the coefﬁcient of friction then has the following form:

¼ K

m1

ð5:6Þ

where C and s are combined into K

. Implicit in this relationship is the additional depen-

dencies on load and other parameters as a result of their ability to inﬂuence tribosurfaces.

These would be contained in K

Abrasive fric tion can be illustrated by considering a cone of included angle F plowing

through a softer surface. For plastic deformation, the force required to do this, F

, is given by

cot FP

ð5:7Þ

where P

is the load on that asperity. For an array of such asperities supporting a total load,

P, F

can be expressed as

¼ K

cot F P ð5:8Þ

where

cot F P  p

1

cot F

ð5:9Þ

In this expression,

cot F reﬂects the average sharpness of the asperities, while

is the parameter accounting for the complete description of the asperity distribu-

tion. The coefﬁcient of friction is then

¼ K

cot F ð5:10Þ

If the cone produced only elastic deformation, there would still be a friction force

and the form of the expression for the coefﬁcient of friction would be similar. However,

in this case, the friction force would be generated by hysteresis. Equation (5.10) would be

modiﬁed by a factor e, which is the ratio of the energy lost to the energy required for the

deformation (10). This similarity of form implies that Eq. (5.10) is also appropriate

for more realistic material behavior, where the deformation contains both an elastic

and plastic portion.

Hysteresis can also be associated with the stress system associated with the macro-

geometry of the contact. In this case, the coefﬁcient of friction is proportional to the stress

level (11). In the elastic co ntact between a sphere and a plane, the stress level is propor-

tional to the P

1=3

and inversely proportional to R

2=3

, where R is radius of the sphere.

The friction force, F

hys

, would be

hys

¼ K

hys

4=3

2=3

ð5:11Þ

and the coefﬁcient of friction would be

hys

¼ K

hys

1=3

2=3

ð5:12Þ

Assume that a fraction of the load, a, is supported by junctions at which adhesion

takes place and the remaining fraction by junctions at which deformation occurs, that is

by adhesion and single-cycle deformation, respectively. For such a situation, the general

expression for the coefﬁcient of friction for a rough sphere sliding on a plane is

m ¼ K

m1

þ K

cot F 1  aðÞþK

hys

1=3

2=3

ð5:13Þ

The observed behavior of the coefﬁcient friction between hardened steel and sheets

of paper, supported by a steel platen, shows the same type of dependencies indicated by

this equation. These data are shown in Figs. (5.3–5.5). These data show the coefﬁcient

of friction to be dependent on the roughness of the sphere, the radius of the sphere, and

the normal load. However, the relationships appear more complex than indicated by

Eq. (5.13). A dependency on paper thickne ss is also evident, which modiﬁes the inﬂu-

ence of load and radius. This effect can be attributed to the inﬂuence that the thickness

of the paper layer has on the nature of the stress system developed in the paper. The

thinner the paper layer , the greater is its apparent stiffness. This is analogous to the

behavior for friction of a layered metallic surface (12,13).

The simple models for the abrasion and adhesion compo nents of friction imply that

under rolling their effects should be eliminated (14). Consequently, rolling friction tests

were conducted to estimate the signiﬁcance of hysteresis in the overall behavior and the

results are shown in Fig. 5.6. It can be seen that while a signiﬁcant load dependency is indi-

cated that is somewhat stronger than that suggested by Eq. (5.13), actual friction is much

lower than for sliding. This suggests that the major contributors to the sliding friction for

this system are adhesion and abrasion. Furthermore, the actual data suggest that m and n

Figure 5.3 Inﬂuence of roughness on the coefﬁcient of friction for sliding between steel and paper.

(From Ref. 6.)

Figure 5.4 Inﬂuence of the radius of a steel slider on the coefﬁcient of friction for sliding between

steel and paper. (From Ref. 6.)

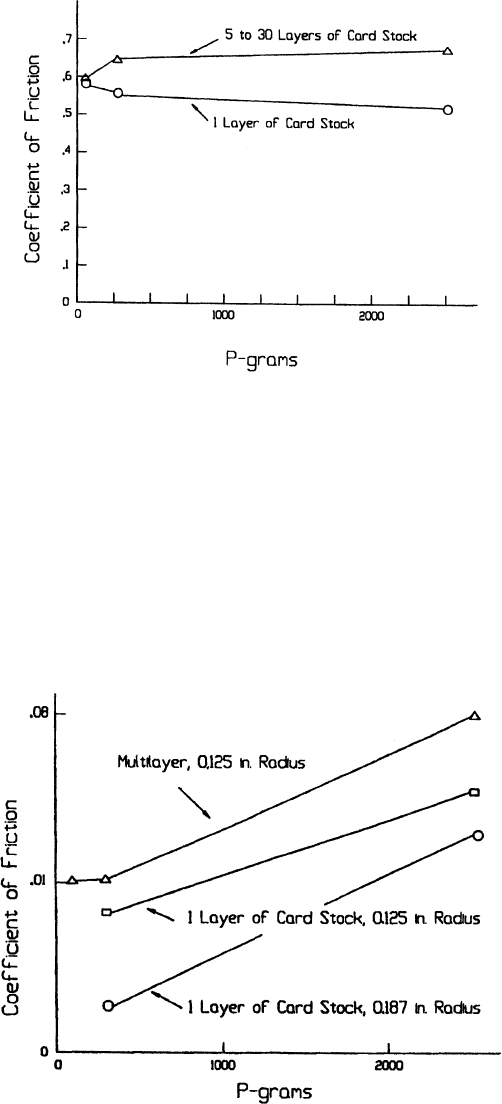
of Eq. (5.6) are close to 1 and 0, respectively. The data also show that size is a signiﬁcant

factor.

While this example of frictional behavior indicates that load and geometry can inﬂu-

ence friction, it also shows that Amontons’ Laws are also approximately followed, that is,

the coefﬁcient of friction is independent of load and geometry. At least over limited

ranges, this situation is true for most material systems, especially those that exhibit low

hysteresis. This would include metals, ceramics, and the more rigid polymers or plastics.

Figure 5.5 Inﬂuence of load on the coefﬁcient of friction for sliding between steel and paper.

(From Ref. 6.)

Figure 5.6 Inﬂuence of load on the coefﬁcient of friction for rolling between a steel sphere and

paper. (From Ref. 6.)

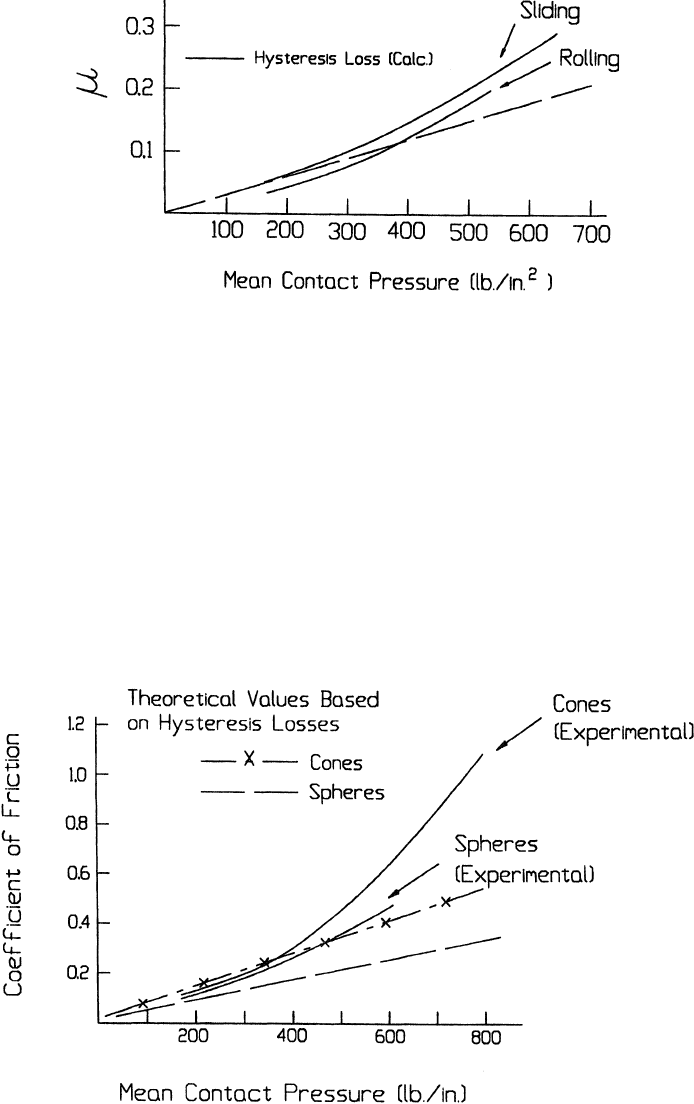
Materials, which tend to exhibit high hysteresis, such as rubbers or elastomers, usually

exhibit a greater effect of load and geometry on the coefﬁcient of friction. Examples of this

behavior are shown in Figs. 5.7 and 5.8.

While the above is generally true, there are examples in which load and geometry

signiﬁcantly inﬂuence friction, independent of a hysteretic effect. Sliding over a woven

surface provides an example of the inﬂuence of geometry and load. Data for such a

situation are shown in Fig. 5.9. Metallic and ceramic sliding systems can also show an

inﬂuence of load on the coefﬁcient of friction. This is generally related to the relationship

between oxide formation and sliding parameters (15,16). The coefﬁcient of friction for

unlubricated, self-mated copper is shown in Fig. 5.10 as a function of load. Two regimes

Figure 5.7 Coefﬁcients of friction for sliding and rolling between a steel sphere and a well-lubri-

cated rubber surface. (From Ref. 26.)

Figure 5.8 Coefﬁcients of friction for spheres and cones sliding on lubricated rubber. (From

Ref. 26.)

of friction behavior are evident as function of load. In each, the coefﬁcient of friction is

independent of load, indicating that within those regimes Amontons’ Law is applicable.

In this particular case, the form ation of different oxides in the two regions is the expla-

nation for this behavior. This is also an example of a transition in friction behavior as a

result of tribosurface modiﬁcation, similar to the transitions in wear behavior.

As shown by the development of Eq. (5.13), roughness can inﬂuence the coefﬁcient

of friction through abrasive and hysteresis effects (17). In addition, roughness can affect

friction behavior through the adhesive mechanisms. In fact, this can be a stronger or more

pronounced effect than those associated with the other two mechanisms, tending to

increase the coefﬁcient of friction, as surfaces become smoother. The coefﬁcient of friction

for clean, self-mated copper surfaces is shown in Fig. 5.10 as a function of roughness. It

can be seen that friction increases much more rapidly for smoother surfaces than it does

for rougher surfa ces. The explanation for this is that as the surfaces become smoother, the

real area increases rapidly and tends to become independent of the load. Perfectly smooth,

ﬂat surfaces result in the real area of contact being equal to the apparent area. Under these

Figure 5.9 Variations of the coefﬁcient of friction for sliding between steel and a lubricated fabric

with different steel geometries. (From Ref. 27.)

conditions, adhesion can be extremely large, with the contact being one large junction.

Consequently, there would be a signiﬁcant increase in the adhesion term, as the surfaces

become smoother. This concept is illustrated in Fig. 5.11.

In the case of rubber, smooth surfaces also introduce additional aspects to friction.

With rubbers, Schall amach waves or waves of detachment occur and can be the prim ary

contributor to the friction between rubber or elastomers and smooth surfaces (5,18).

Fig. 5.12 illustrates this. In this situation, there is strong local adhesion between the rubber

surface and the counterface. As sliding occurs, local regions remain attached, at least up to

a certain point. Then the bond is broken and the rubber snaps forward. At some point, it

again adheres and the process repeats. This process can be viewed as waves, which propa-

gate across the rubber surface. Examinations of sliding contacts and wear scar morphology

suggest this behavior as well. This is shown by the examples in Fig. 5.13. In this case, the

friction force is associa ted with adhesion as well as with hysteresis losses in the stretch-

ing of the rubber. The following equation has been proposed for this mechanism (5):

m ¼



s½ 2=e

ðÞþ1

1=2

ð5:14Þ

where e

is the compressive strain; G, the loss portion of the complex shear modulus;

and s

the mean pressure.

Figure 5.10 Coefﬁcient of friction for unlubricated sliding between Cu surfaces. (‘‘A’’ from Ref.

28; ‘‘B’’ from Ref. 29.)

Figure 5.11 Changes in the ratio of the real and apparent areas of contact as a function of load and

roughness.

Figure 5.12 Illustration of the propagation of Schallamach waves across a rubber surface (trun-

cated cone in ﬁgure) during sliding on a ﬂat surface. (From Ref. 18.)

Figure 5.13 Examples of the wave-like wear scar morphology frequently observed on elastomer

surfaces as a result of sliding. (‘‘A’’ from Ref. 30, reprinted with permission from ASTM.)

While the simple models used to describe the mechanisms associated with friction

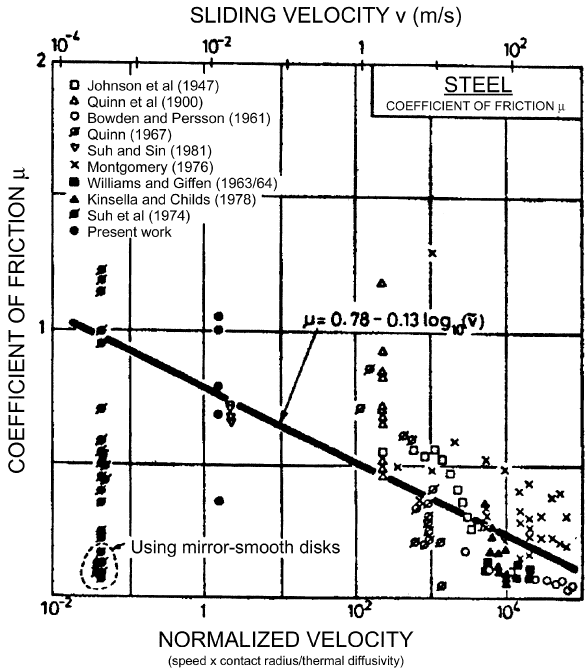
do not explicitly indicate a dependency on sliding velocity, most systems exhibit some

velocity effect. The effect is relatively mild for most engineering materials as changes

of several orders of magnitude in sliding velocity might result in less than a factor of

2 change in friction. An example is shown in Fig. 5.14. In this ﬁgure, the coefﬁcient

of friction for unlubricated sliding between steel surfaces is plotted as a function of

speed. There can be several reasons for a dependency on speed and the speciﬁc reason

is usually related to the material or materials involved. For material s, which exhibit

creep, such as soft metals and polymers, it is usually associated with viscoelastic beha-

vior of such materials. For such materials, friction usually achieves a maximum value in

a particular range of velocity. For other types of materials, friction generally tends to

decrease with sliding. Melting and softening at higher speeds can also be a factor, as

in the case with polymers, and oxide formation can be a factor in metal systems, as

is the case with the data shown in Fig. 5.15. Junction growth phenomena can also con-

tribute to this decrease in friction. This is because junction size tends to increase with

time under shear (19). There will be less time for growth at higher sliding speeds. Smaller

Figure 5.14 Variation in the coefﬁcient of friction with sliding velocity for unlubricated steel.

(From Ref. 31, reprinted with permission from Elsevier Science Publishers.)

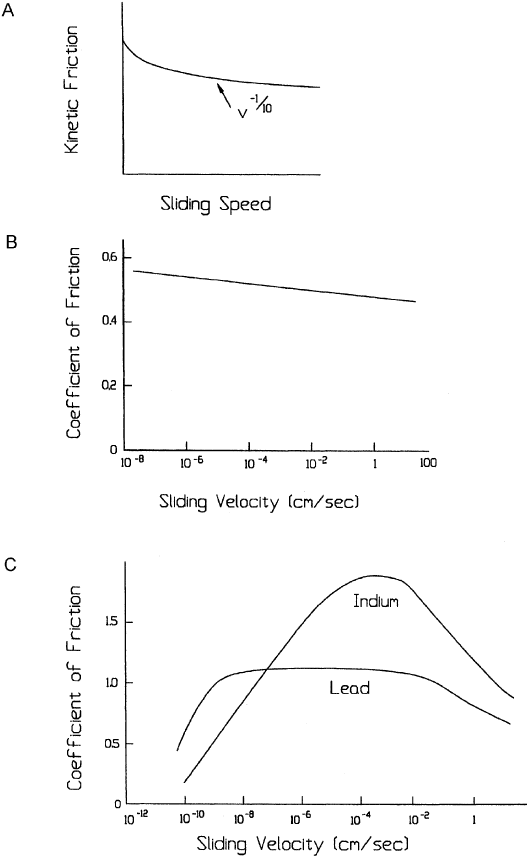
junctions result in less real area of contact and a lower adhesion contribution to friction.

The graphs in Fig. 5.15 show some examples of this type of behavior.

Because of the adhesive component of friction, friction behavior is very sensitive to

surface ﬁlm and layer s, particularly in unlubricated situations. The effect of oxide for-

mation on the coefﬁcient of friction and the effect of humidity illustrate this. Another

example is surface contamination from handling or exposure to contaminating environ-

ments. With metals, this can often reduce the coefﬁcient of fri ction from a value near

1 to 0.3–0.6.

Figure 5.15 Effects of sliding speed on the coefﬁcient of friction for several systems. ‘‘A’’, general

trend; ‘‘B’’, Ti=Ti unlubricated; and ‘‘C’’, steel against Pd and In. (From Ref. 31.)