Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials

Подождите немного. Документ загружается.

Apago PDF Enhancer

147

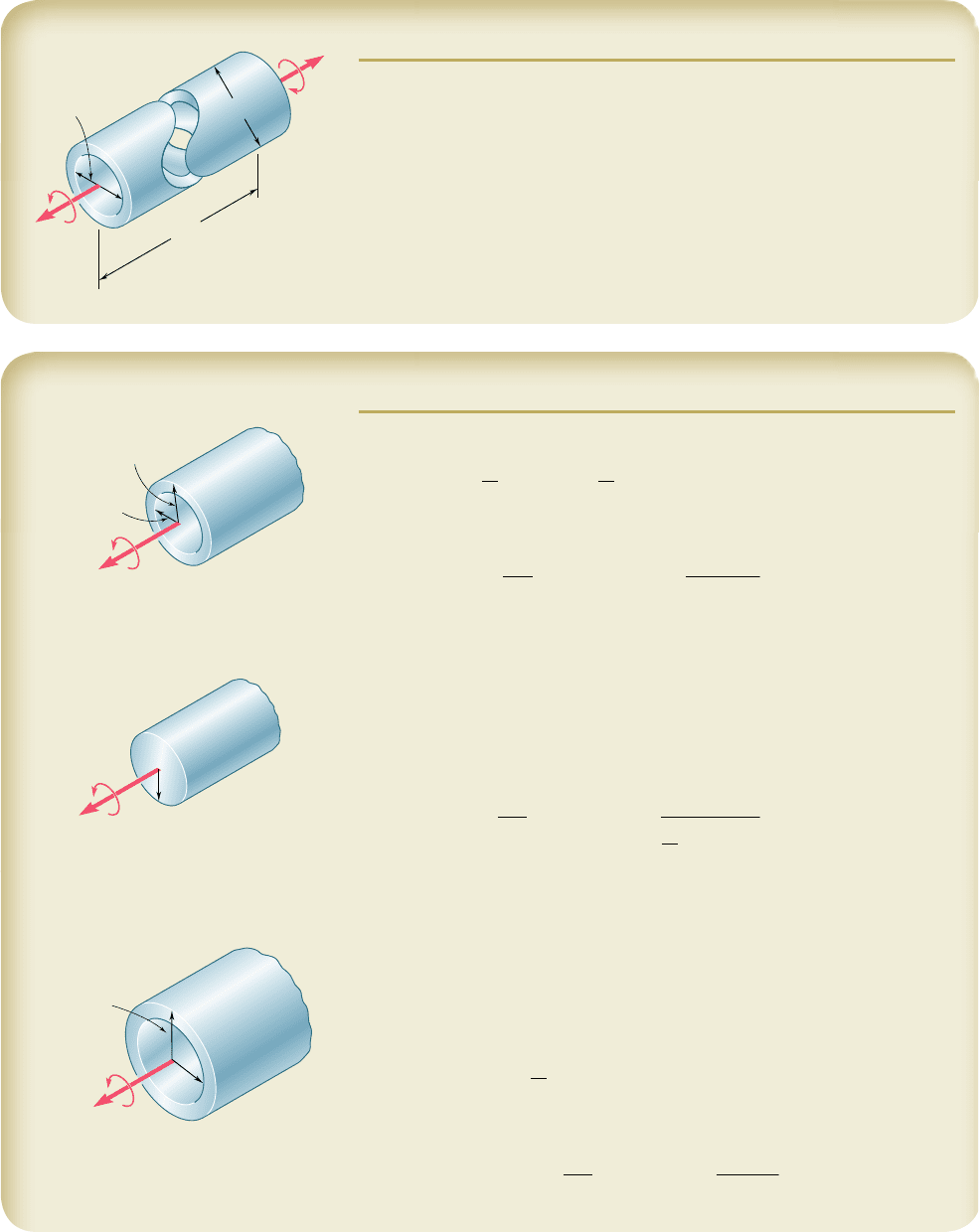
Our discussion so far has ignored the mode of application of the

twisting couples T and T9. If all sections of the shaft, from one end to

the other, are to remain plane and undistorted, we must make sure that

the couples are applied in such a way that the ends of the shaft them-

selves remain plane and undistorted. This may be accomplished by

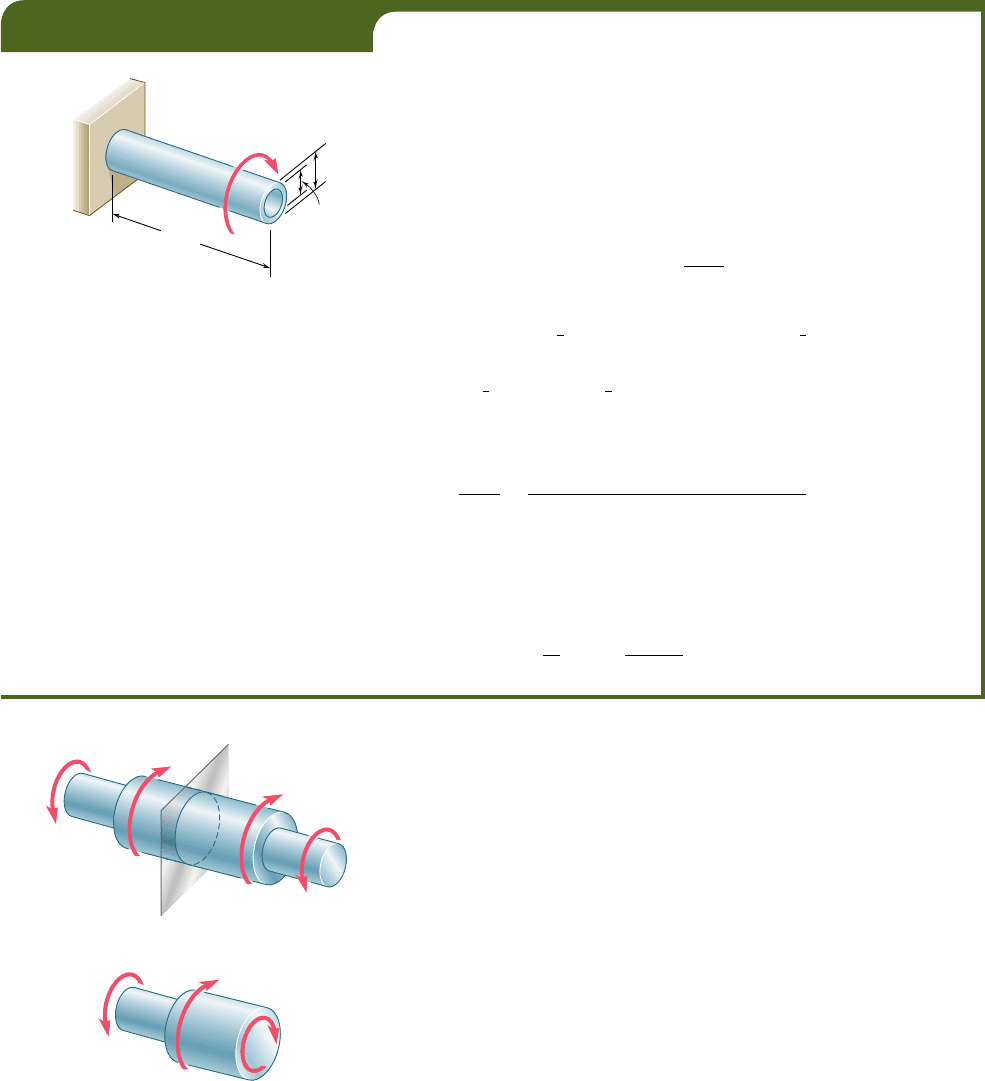
applying the couples T and T9 to rigid plates, which are solidly attached

to the ends of the shaft (Fig. 3.12a). We can then be sure that all sec-

tions will remain plane and undistorted when the loading is applied,

and that the resulting deformations will occur in a uniform fashion

throughout the entire length of the shaft. All of the equally spaced cir-

cles shown in Fig. 3.12a will rotate by the same amount relative to their

neighbors, and each of the straight lines will be transformed into a curve

(helix) intersecting the various circles at the same angle (Fig. 3.12b).

The derivations given in this and the following sections will be

based on the assumption of rigid end plates. Loading conditions

encountered in practice may differ appreciably from those corre-

sponding to the model of Fig. 3.12. The chief merit of this model is

that it helps us define a torsion problem for which we can obtain an

exact solution, just as the rigid-end-plates model of Sec. 2.17 made

it possible for us to define an axial-load problem which could be

easily and accurately solved. By virtue of Saint-Venant’s principle, the

results obtained for our idealized model may be extended to most

engineering applications. However, we should keep these results

associated in our mind with the specific model shown in Fig. 3.12.

We will now determine the distribution of shearing strains in

a circular shaft of length L and radius c that has been twisted through

an angle f (Fig. 3.13a). Detaching from the shaft a cylinder of radius

r, we consider the small square element formed by two adjacent

circles and two adjacent straight lines traced on the surface of the

cylinder before any load is applied (Fig. 3.13b). As the shaft is

subjected to a torsional load, the element deforms into a rhombus

(Fig. 3.13c). We now recall from Sec. 2.14 that the shearing strain g

in a given element is measured by the change in the angles formed

by the sides of that element. Since the circles defining two of the

sides of the element considered here remain unchanged, the shear-

ing strain g must be equal to the angle between lines AB and A9B.

(We recall that g should be expressed in radians.)

We observe from Fig. 3.13c that, for small values of g, we can

express the arc length AA9 as AA9 5 Lg. But, on the other hand, we

have AA9 5 rf. It follows that Lg 5 rf, or

g 5

(3.2)

where g and f are both expressed in radians. The equation obtained

shows, as we could have anticipated, that the shearing strain g at a

given point of a shaft in torsion is proportional to the angle of twist

f. It also shows that g is proportional to the distance r from the axis

of the shaft to the point under consideration. Thus, the shearing

strain in a circular shaft varies linearly with the distance from the

axis of the shaft.

3.3 Deformations in a Circular Shaft

(b)

(a)

Fig. 3.12 Deformation of shaft

subject to twisting couples.

(a)

(b)

(c)

␾

␥

␳

␾

Fig. 3.13 Shearing strain.

bee80288_ch03_140-219.indd Page 147 9/21/10 3:04:11 PM user-f499bee80288_ch03_140-219.indd Page 147 9/21/10 3:04:11 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

148

Torsion

It follows from Eq. (3.2) that the shearing strain is maximum

on the surface of the shaft, where r 5 c. We have

max

(3.3)

Eliminating f from Eqs. (3.2) and (3.3), we can express the shearing

strain g at a distance r from the axis of the shaft as

g 5

max

(3.4)

3.4 STRESSES IN THE ELASTIC RANGE

No particular stress-strain relationship has been assumed so far in our

discussion of circular shafts in torsion. Let us now consider the case

when the torque T is such that all shearing stresses in the shaft remain

below the yield strength t

. We know from Chap. 2 that, for all practi-

cal purposes, this means that the stresses in the shaft will remain below

the proportional limit and below the elastic limit as well. Thus, Hooke’s

law will apply and there will be no permanent deformation.

Recalling Hooke’s law for shearing stress and strain from Sec.

2.14, we write

t 5 Gg (3.5)

where G is the modulus of rigidity or shear modulus of the material.

Multiplying both members of Eq. (3.4) by G, we write

Gg 5

max

or, making use of Eq. (3.5),

t 5

max

(3.6)

The equation obtained shows that, as long as the yield strength (or

proportional limit) is not exceeded in any part of a circular shaft, the

shearing stress in the shaft varies linearly with the distance r from

the axis of the shaft. Figure 3.14a shows the stress distribution in a

solid circular shaft of radius c, and Fig. 3.14b in a hollow circular

shaft of inner radius c

and outer radius c

. From Eq. (3.6), we find

that, in the latter case,

min

max

(3.7)

We now recall from Sec. 3.2 that the sum of the moments of

the elementary forces exerted on any cross section of the shaft must

be equal to the magnitude T of the torque exerted on the shaft:

er(t dA) 5 T (3.1)

bee80288_ch03_140-219.indd Page 148 9/21/10 3:04:16 PM user-f499bee80288_ch03_140-219.indd Page 148 9/21/10 3:04:16 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

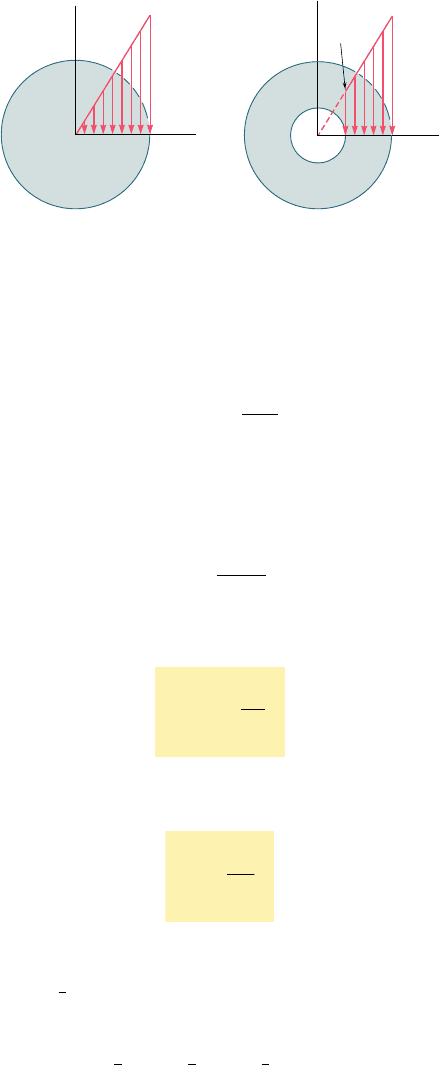
Apago PDF Enhancer

149

Substituting for t from (3.6) into (3.1), we write

T 5

rt dA 5

max

But the integral in the last member represents the polar moment of

inertia J of the cross section with respect to its center O. We have

therefore

T 5

max

(3.8)

or, solving for t

max

(3.9)

Substituting for t

max

from (3.9) into (3.6), we express the shearing

stress at any distance r from the axis of the shaft as

t 5

(3.10)

Equations (3.9) and (3.10) are known as the elastic torsion formulas.

We recall from statics that the polar moment of inertia of a circle of

radius c is

. In the case of a hollow circular shaft of inner

radius c

and outer radius c

, the polar moment of inertia is

J 5

p 1c

2 c

2 (3.11)

We note that, if SI metric units are used in Eq. (3.9) or (3.10),

T will be expressed in N ? m, c or r in meters, and J in m

; we check

that the resulting shearing stress will be expressed in N/m

, that is,

pascals (Pa). If U.S. customary units are used, T should be expressed

in lb ? in., c or r in inches, and J in in

, with the resulting shearing

stress expressed in psi.

3.4 Stresses in the Elastic Range

max

␶

max

␶

min

␶

(a)

(b)

␶

␳

␶

␳

Fig. 3.14 Distribution of shearing stresses.

bee80288_ch03_140-219.indd Page 149 9/21/10 3:04:17 PM user-f499bee80288_ch03_140-219.indd Page 149 9/21/10 3:04:17 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

150

EXAMPLE 3.01

A hollow cylindrical steel shaft is 1.5 m long and has inner and outer

diameters respectively equal to 40 and 60 mm (Fig. 3.15). (a) What is the

largest torque that can be applied to the shaft if the shearing stress is not

to exceed 120 MPa? (b) What is the corresponding minimum value of the

shearing stress in the shaft?

(a) Largest Permissible Torque. The largest torque T that can

be applied to the shaft is the torque for which t

max

5 120 MPa. Since

this value is less than the yield strength for steel, we can use Eq. (3.9).

Solving this equation for T, we have

T 5

max

(3.12)

Recalling that the polar moment of inertia J of the cross section is given by

Eq. (3.11), where

40 mm

5 0.02 m and

60 mm

5 0.03 m,

we write

p 1c

2 c

p10.03

2 0.02

25 1.021 3 10

Substituting for J and t

max

into (3.12), and letting c 5 c

5 0.03 m, we

have

T 5

max

11.021 3 10

21120 3 10

Pa2

0.03 m

5 4.08 kN ? m

(b) Minimum Shearing Stress. The minimum value of the shear-

ing stress occurs on the inner surface of the shaft. It is obtained from Eq.

(3.7), which expresses that t

min

and t

max

are respectively proportional to

and c

min

max

0.02 m

0.03 m

1120 MPa25 80 MPa

1.5 m

40 mm

60 mm

Fig. 3.15

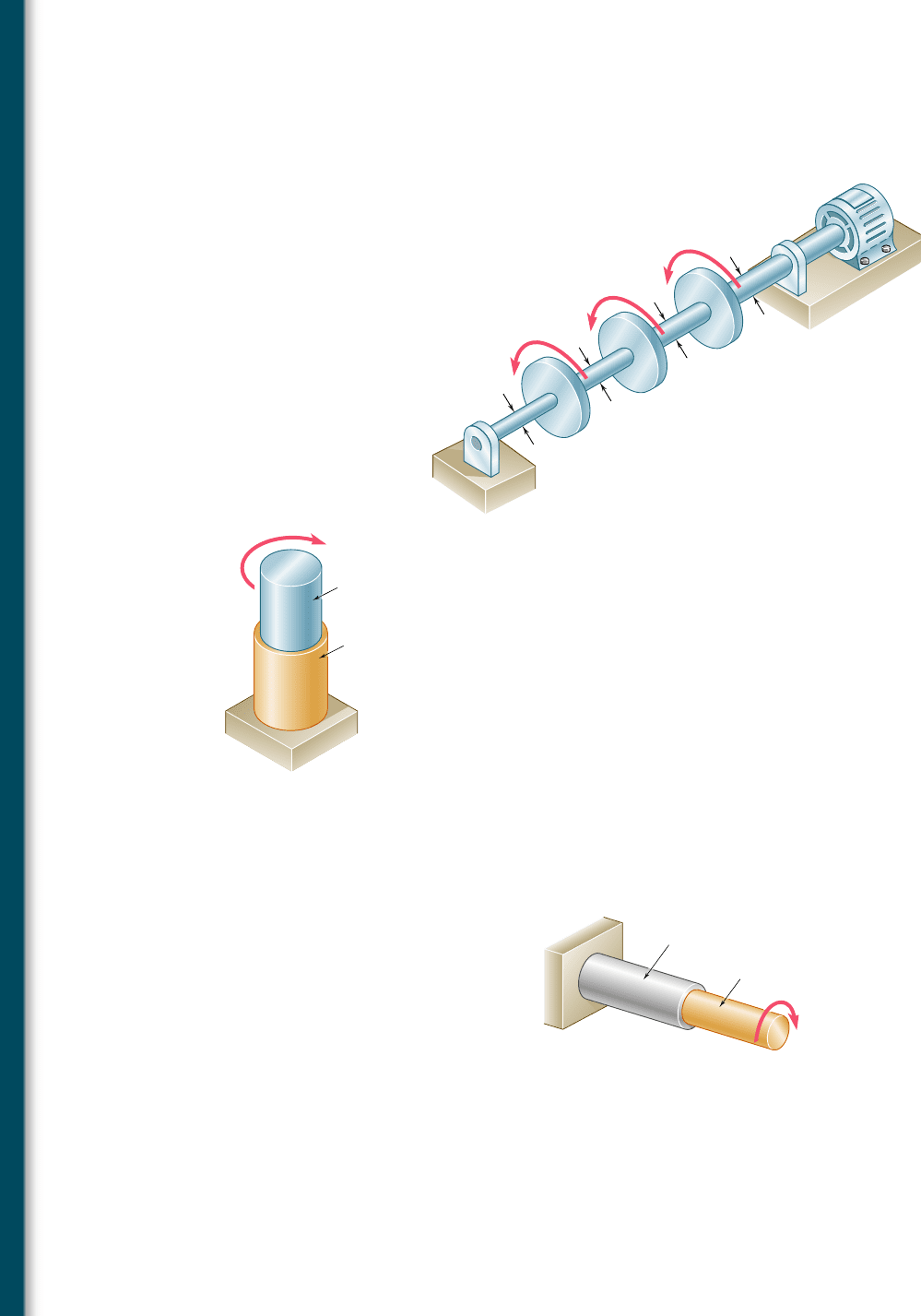
The torsion formulas (3.9) and (3.10) were derived for a shaft

of uniform circular cross section subjected to torques at its ends.

However, they can also be used for a shaft of variable cross section

or for a shaft subjected to torques at locations other than its ends

(Fig. 3.16a). The distribution of shearing stresses in a given cross

section S of the shaft is obtained from Eq. (3.9), where J denotes the

polar moment of inertia of that section, and where T represents the

internal torque in that section. The value of T is obtained by drawing

the free-body diagram of the portion of shaft located on one side of

the section (Fig. 3.16b) and writing that the sum of the torques

applied to that portion, including the internal torque T, is zero (see

Sample Prob. 3.1).

Up to this point, our analysis of stresses in a shaft has been

limited to shearing stresses. This is due to the fact that the element

we had selected was oriented in such a way that its faces were either

parallel or perpendicular to the axis of the shaft (Fig. 3.5). We know

from earlier discussions (Secs. 1.11 and 1.12) that normal stresses,

shearing stresses, or a combination of both may be found under the

same loading condition, depending upon the orientation of the

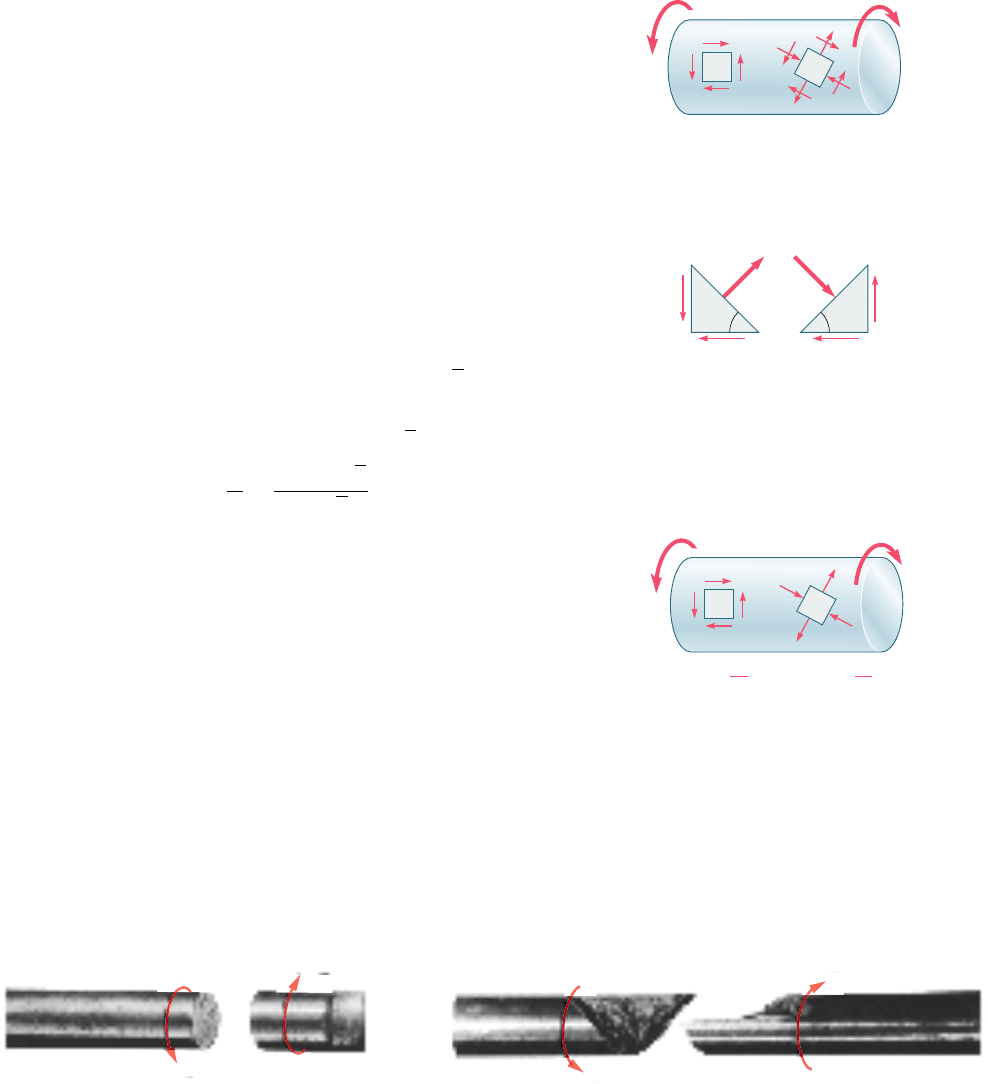
element that has been chosen. Consider the two elements a and

b located on the surface of a circular shaft subjected to torsion

(a)

(b)

Fig. 3.16 Shaft with variable cross

section.

bee80288_ch03_140-219.indd Page 150 11/2/10 12:48:16 AM user-f499bee80288_ch03_140-219.indd Page 150 11/2/10 12:48:16 AM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

151

(Fig. 3.17). Since the faces of element a are respectively parallel and

perpendicular to the axis of the shaft, the only stresses on the ele-

ment will be the shearing stresses defined by formula (3.9), namely

max

5 TcyJ. On the other hand, the faces of element b, which form

arbitrary angles with the axis of the shaft, will be subjected to a

combination of normal and shearing stresses.

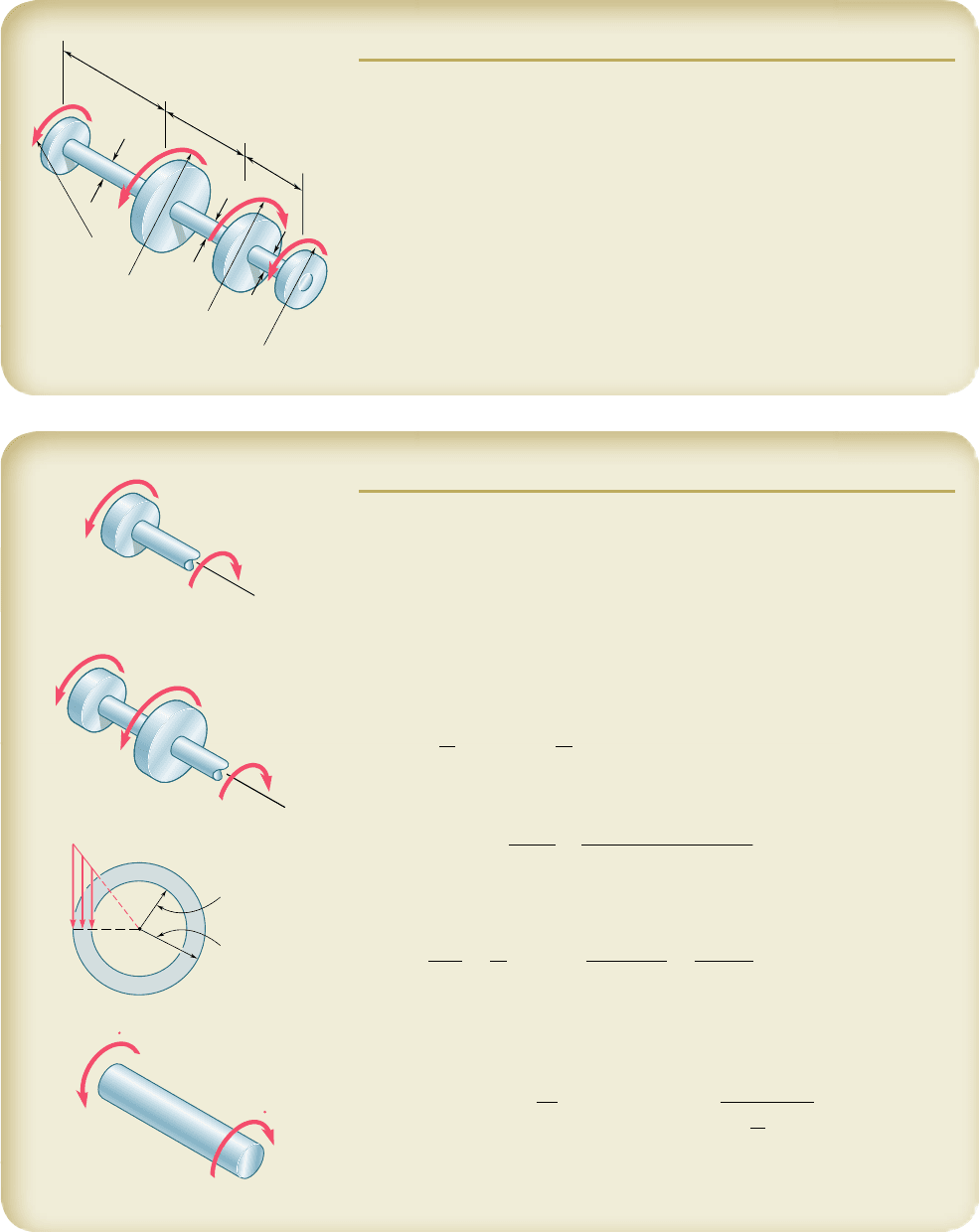
Let us consider the stresses and resulting forces on faces that

are at 458 to the axis of the shaft. In order to determine the stresses

on the faces of this element, we consider the two triangular elements

shown in Fig. 3.18 and draw their free-body diagrams. In the case

of the element of Fig. 3.18a, we know that the stresses exerted on

the faces BC and BD are the shearing stresses t

max

5 TcyJ. The

magnitude of the corresponding shearing forces is thus t

max

, where

denotes the area of the face. Observing that the components along

DC of the two shearing forces are equal and opposite, we conclude

that the force F exerted on DC must be perpendicular to that face.

It is a tensile force, and its magnitude is

F 5 21t

max

2cos 45° 5 t

max

12 (3.13)

The corresponding stress is obtained by dividing the force F by the

area A of face DC. Observing that A 5 A

12, we write

s 5

max

5 t

max

(3.14)

A similar analysis of the element of Fig. 3.18b shows that the stress

on the face BE is s 5 2t

max

. We conclude that the stresses exerted

on the faces of an element c at 458 to the axis of the shaft (Fig. 3.19)

are normal stresses equal to 6t

max

. Thus, while the element a in

Fig. 3.19 is in pure shear, the element c in the same figure is sub-

jected to a tensile stress on two of its faces, and to a compressive

stress on the other two. We also note that all the stresses involved

have the same magnitude, TcyJ.†

As you learned in Sec. 2.3, ductile materials generally fail in

shear. Therefore, when subjected to torsion, a specimen J made of

a ductile material breaks along a plane perpendicular to its longitu-

dinal axis (Photo 3.2a). On the other hand, brittle materials are

weaker in tension than in shear. Thus, when subjected to torsion, a

specimen made of a brittle material tends to break along surfaces

that are perpendicular to the direction in which tension is maximum,

i.e., along surfaces forming a 458 angle with the longitudinal axis of

the specimen (Photo 3.2b).

3.4 Stresses in the Elastic Range

†Stresses on elements of arbitrary orientation, such as element b of Fig. 3.18, will be dis-

cussed in Chap. 7.

Photo 3.2 Shear failure of shaft subject to torque.

(

)

Ducti

ure

(

)

Britt

max

␶

Fig. 3.17 Circular shaft with

elements at different orientations.

(a)(b)

CCBB

max

␶

max

␶

max

␶

max

␶

45⬚

FF'

Fig. 3.18 Forces on faces at 458 to

shaft axis.

⫽

max

␶

⫽⫾

45⬚

␴

Fig. 3.19 Shaft with elements with

only shear stresses or normal stresses.

bee80288_ch03_140-219.indd Page 151 9/21/10 3:04:24 PM user-f499bee80288_ch03_140-219.indd Page 151 9/21/10 3:04:24 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

152

SAMPLE PROBLEM 3.1

Shaft BC is hollow with inner and outer diameters of 90 mm and 120 mm,

respectively. Shafts AB and CD are solid and of diameter d. For the loading

shown, determine (a) the maximum and minimum shearing stress in shaft

BC, (b) the required diameter d of shafts AB and CD if the allowable shear-

ing stress in these shafts is 65 MPa.

0.9 m

0.7 m

0.5 m

120 mm

 6 kN · m

 14 kN · m

 26 kN · m

 6 kN · m

SOLUTION

Equations of Statics. Denoting by T

the torque in shaft AB, we

pass a section through shaft AB and, for the free body shown, we write

©M

5 0:

6 kN ? m

2 T

5 0T

5 6 kN ? m

We now pass a section through shaft BC and, for the free body shown, we

have

©M

5 0:

6 kN ? m

14 kN ? m

2 T

5 0T

5 20 kN ? m

a. Shaft BC. For this hollow shaft we have

J 5

2 c

310.0602

2 10.0452

45 13.92 3 10

Maximum Shearing Stress. On the outer surface, we have

max

5 t

20 kN ? m



0.060 m

13.92 3 10

max

5 86.2 MPab

Minimum Shearing Stress. We write that the stresses are propor-

tional to the distance from the axis of the shaft.

min

max



min

86.2 MPa

45 mm

60 mm

5 64.7 MPab

b. Shafts AB and CD. We note that in both of these shafts the mag-

nitude of the torque is T 5 6 kN ? m and t

all

5 65 MPa. Denoting by c

the radius of the shafts, we write

t 5

65 MPa 5

6 kN ? m

5 58

8 3 10





5 38

9 3 10

5 2c 5 2138.9 mm2

5 77

8 mmb

 6 kN · m

 14 kN · m

 45 mm

 60 mm



6 kN · m

6 kN ·

bee80288_ch03_140-219.indd Page 152 9/21/10 3:04:31 PM user-f499bee80288_ch03_140-219.indd Page 152 9/21/10 3:04:31 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

153

SAMPLE PROBLEM 3.2

The preliminary design of a large shaft connecting a motor to a generator

calls for the use of a hollow shaft with inner and outer diameters of 4 in.

and 6 in., respectively. Knowing that the allowable shearing stress is 12 ksi,

determine the maximum torque that can be transmitted (a) by the shaft as

designed, (b) by a solid shaft of the same weight, (c) by a hollow shaft of

the same weight and of 8-in. outer diameter.

8 ft

6 in.

4 in.

SOLUTION

a. Hollow Shaft as Designed. For the hollow shaft we have

J 5

2 c

313 in.2

2 12 in.2

45 102.1 in

Using Eq. (3.9), we write

max

12 ksi 5

T13 in.

102.1 in

T 5 408

ip ? in.b

b. Solid Shaft of Equal Weight. For the shaft as designed and this

solid shaft to have the same weight and length, their cross-sectional areas

must be equal.

1a2

5 A

1b2

p 313 in.2

2 12 in.2

45 pc





5 2.24 in.

Since t

all

5 12 ksi, we write

max

12 ksi 5

T12.24 in.2

12.24 in.2

T 5 211

ip ? in.b

c. Hollow Shaft of 8-in. Diameter. For equal weight, the cross-

sectional areas again must be equal. We determine the inside diameter of

the shaft by writing

1a2

5 A

1c2

p 313 in.2

2 12 in.2

45 p 314 in.2

2 c

4



5 3.317 in.

For c

5 3.317 in. and c

5 4 in.,

J 5

314 in.2

2 13.317 in.2

45 212 in

With t

all

5 12 ksi and c

5 4 in.,

max

12 ksi 5

T14 in.

212 in

T 5 636

ip ? in.b

⫽ 3 in.

⫽ 2 in.

⫽ 4 in.

bee80288_ch03_140-219.indd Page 153 9/21/10 9:15:26 PM user-f499bee80288_ch03_140-219.indd Page 153 9/21/10 9:15:26 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

PROBLEMS

154

3.1 (a) Determine the maximum shearing stress caused by a 4.6-kN ? m

torque T in the 76-mm-diameter solid aluminum shaft shown.

(b) Solve part a, assuming that the solid shaft has been replaced by

a hollow shaft of the same outer diameter and of 24-mm inner

diameter.

3.2 (a) Determine the torque T that causes a maximum shearing stress

of 45 MPa in the hollow cylindrical steel shaft shown. (b) Deter-

mine the maximum shearing stress caused by the same torque T

in a solid cylindrical shaft of the same cross-sectional area.

76 mm

1.2 m

Fig. P3.1

3.3 Knowing that d 5 1.2 in., determine the torque T that causes a

maximum shearing stress of 7.5 ksi in the hollow shaft shown.

3.4 Knowing that the internal diameter of the hollow shaft shown is

d 5 0.9 in., determine the maximum shearing stress caused by a

torque of magnitude T 5 9 kip ? in.

3.5 A torque T 5 3 kN ? m is applied to the solid bronze cylinder

shown. Determine (a) the maximum shearing stress, (b) the shear-

ing stress at point D, which lies on a 15-mm-radius circle drawn

on the end of the cylinder, (c) the percent of the torque carried

by the portion of the cylinder within the 15-mm radius.

2.4 m

30 mm

45 mm

Fig. P3.2

1.6 in.

Fig. P3.3 and P3.4

60 mm

30 mm

200 mm

T  3 kN · m

Fig. P3.5

3.6 (a) Determine the torque that can be applied to a solid shaft of

20-mm diameter without exceeding an allowable shearing stress of

80 MPa. (b) Solve part a, assuming that the solid shaft has been

replaced by a hollow shaft of the same cross-sectional area and with

an inner diameter equal to half of its outer diameter.

bee80288_ch03_140-219.indd Page 154 9/21/10 3:04:51 PM user-f499bee80288_ch03_140-219.indd Page 154 9/21/10 3:04:51 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

155

Problems

3.7 The solid spindle AB has a diameter d

5 1.5 in. and is made of

a steel with an allowable shearing stress of 12 ksi, while sleeve CD

is made of a brass with an allowable shearing stress of 7 ksi. Deter-

mine the largest torque T that can be applied at A.

3.8 The solid spindle AB is made of a steel with an allowable shearing

stress of 12 ksi, and sleeve CD is made of a brass with an allowable

shearing stress of 7 ksi. Determine (a) the largest torque T that

can be applied at A if the allowable shearing stress is not to be

exceeded in sleeve CD, (b) the corresponding required value of

the diameter d

of spindle AB.

3.9 The torques shown are exerted on pulleys A and B. Knowing that

both shafts are solid, determine the maximum shearing stress in

(a) in shaft AB, (b) in shaft BC.

4 in.

8 in.

t 

in.

3 in.

Fig. P3.7 and P3.8

30 mm

46 mm

 300 N · m

 400 N · m

Fig. P3.9

3.10 In order to reduce the total mass of the assembly of Prob. 3.9, a

new design is being considered in which the diameter of shaft BC

will be smaller. Determine the smallest diameter of shaft BC for

which the maximum value of the shearing stress in the assembly

will not increase.

3.11 Knowing that each of the shafts AB, BC, and CD consists of a solid

circular rod, determine (a) the shaft in which the maximum shear-

ing stress occurs, (b) the magnitude of that stress.

 21 mm

 18 mm

60 N · m

48 N · m

 15 mm

144 N · m

Fig. P3.11 and P3.12

3.12 Knowing that an 8-mm-diameter hole has been drilled through each

of the shafts AB, BC, and CD, determine (a) the shaft in which the

maximum shearing stress occurs, (b) the magnitude of that stress.

bee80288_ch03_140-219.indd Page 155 9/21/10 3:05:08 PM user-f499bee80288_ch03_140-219.indd Page 155 9/21/10 3:05:08 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

156

Torsion

3.13 Under normal operating conditions, the electric motor exerts a

12-kip ? in. torque at E. Knowing that each shaft is solid, deter-

mine the maximum shearing stress in (a) shaft BC, (b) shaft CD,

2.25 in.

2 in.

1.75 in.

1.50 in.

5 kip · in.

4 kip · in.

3 kip · in.

Fig. P3.13

3.14 Solve Prob. 3.13, assuming that a 1-in.-diameter hole has been

drilled into each shaft.

3.15 The allowable shearing stress is 15 ksi in the 1.5-in.-diameter steel

rod AB and 8 ksi in the 1.8-in.-diameter brass rod BC. Neglecting

the effect of stress concentrations, determine the largest torque

that can be applied at A.

3.16 The allowable shearing stress is 15 ksi in the steel rod AB and

8 ksi in the brass rod BC. Knowing that a torque of magnitude

T 5 10 kip ? in. is applied at A, determine the required diameter

of (a) rod AB, (b) rod BC.

3.17 The allowable stress is 50 MPa in the brass rod AB and 25 MPa

in the aluminum rod BC. Knowing that a torque of magnitude

T 5 1250 N ? m is applied at A, determine the required diameter

of (a) rod AB, (b) rod BC.

Brass

Steel

Fig. P3.15 and P3.16

Brass

Aluminum

Fig. P3.17 and P3.18

3.18 The solid rod BC has a diameter of 30 mm and is made of an alu-

minum for which the allowable shearing stress is 25 MPa. Rod AB

is hollow and has an outer diameter of 25 mm; it is made of a brass

for which the allowable shearing stress is 50 MPa. Determine (a) the

largest inner diameter of rod AB for which the factor of safety is the

same for each rod, (b) the largest torque that can be applied at A.

bee80288_ch03_140-219.indd Page 156 9/21/10 3:05:18 PM user-f499bee80288_ch03_140-219.indd Page 156 9/21/10 3:05:18 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03