Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

s24.2 The Flux Expressions for Heat and Mass

767

with

In a,), pressure diffusion (term with Vp), and forced diffusion (term with

g).

The d,

are so defined that Z,d,

The entropy production in Eq. 24.1-6, which is a sum of products of fluxes and

forces, is the starting point for the nonequilibrium thermodynamics development. Ac-

cording to the "linearity postulate" each of the fluxes in Eq. 24.1-6 (q'"',

j,,

and

G,/M,)

can be written as a linear function of all the forces (VT,

d,,

Vv,

and r,). How-

ever, because of "Curie's postulate," each of the

must depend linearly on all of the

d, as well as on VT, and

q(h)

must depend linearly on VT as well as on all the d,, but

neither

nor

q(h)

can depend on Vv or r,. Similarly the stress tensor

will depend on

the tensor

Vv,

and also on the scalar driving forces r, multiplied by the unit tensor.

Since the "coupling" between

and the chemical reactions has not been studied, we

omit any further consideration of it. In the next section we discuss the coupling among

all the vector forces and vector fluxes and the consequences of applying the "Onsager

reciprocal relations."

524.2

THE FLUX EXPRESSIONS FOR HEAT

AND

MASS

We now employ the "linearity postulate" to obtain for the vector fluxes

In these equations the quantities a,,,, a,,, a,,, and

asp

are the "phenomenological coeffi-

cients" (that is, the transport properties). Because the

and d, are not all independent, it

must be required that a,,

2,a,,

where the sums are over all

(except

from

Now according to the Onsager reciprocal relations, a,,

a,,

and

nap

a,,

for all

values of

and /3 from

Next we relate the phenomenological coefficients to the transport coefficients. First

we relabel a,, and ao, as

D:,

the multicomponent thermal diffusion coefficients. These have

the property that

2,~:

Then we define the multicomponent Fick difisivities,'

ID,,,

D,,

-cRTaap/papp. These diffusivities are symmetric (Elap

D,,)

and obey the rela-

tions C,U,D,~

Then Eq. 24.2-2 becomes

for the multicomponent mass fluxes. These are the generalized Fick equations. When the

second form of

Eq.

24.1-8 is substituted into

Eq.

24.2-3 we see that there are four contri-

butions to the mass-flux vector

j,:

the concentration diffusion term (containing the activ-

ity gradient), the pressure diffusion term (containing the pressure gradient), the forced

diffusion term (containing the external forces), and the thermal diffusion term (propor-

tional to the temperature gradient).

Curtiss,

Chem. Pkys.,

49,2917-2919 (1968); see also

Condiff,

Chem. Pkys.,

51,

42094212 (1969), and C.

Curtiss

and

Bird,

Ind.

Eng. Chem. Research,

39,2515-2522 (1999); errata

41,1791 (2001). The

Dap

used here are the negatives

the

Curtiss

D,~,

which, in turn, are different from

the

DaB

used

Hirschfelder, C.

Curtiss, and

Bird,

Molecular

Theo

of Gases

and

Liquids,

Wiley, New York (1954), second corrected printing (1964, Chapter 11.

768

Chapter

Other Mechanisms for Mass Transport

Equation 24.2-3 can be turned "wrong-side out"',' and solved for the driving forces d,:

These are the generalized Maxwell-Stefan equations, a special case of which was given in

Eq. 17.9-1. The

Bop

are called the mulficomponent Maxwell-Stefan diffusivities, and they

have been proven to be ~ymrnetric;~ their relation to the Dap will be discussed presently.

When the expression for d, in Eq. 24.2-4 is substituted into Eq. 24.2-1, we get

The thermal conductivity of a mixture is defined to be the coefficient of proportionality

between the heat-flux vector and the temperature gradient when there are no mass

fluxes in the system. Thus, the quantity in brackets is, by general agreement, the thermal

conductivity

times the absolute temperature

If we combine this result with the defin-

ition in

Eq.

24.1-7, w get for the final expression for the heat flux:3

We see that the heat flux vector

consists of three terms: the heat conduction term (con-

taining the thermal conductivity), the heat diffusion term (containing the partial molar

enthalpies and the mass fluxes), and finally the Dufour term (containing the thermal dif-

fusion coefficients and the mass fluxes). The heat diffusion term, already encountered in

Eq. 19.3-3, is generally important in diffusing systems. The Dufour term is usually small

and can usually be neglected.

Equations 24.2-3,4, and

are the principal results of nonequilibrium thermodynam-

ics. We now have the mass- and heat-flux vectors expressed in terms of the transport

properties and the fluxes.

Next we discuss the relation between the matrix of Fick diffusivities

Dep

and that of

the Maxwell-Stefan diffusivities

Bag.

Both matrices are symmetric and of order

and both have

~N(N

1) independent elements. The

Bap

are obtained thus:3

in which

(Ba)pY

DPy

Day-that is, the

y-component of a matrix called

B,,

which is

of order (N

1)-and adj

is the matrix adjoint to

B,.

For binary and ternary

Merk,

Appl.

Sci.

Res.,

A8,73-99 (1959);

Helfand,

Chem.

Phys.,

33,319-322 (1960).

Hendrik

Jacobus

Merk

(1920-1988) performed the inversion of the mass-flux expressions when he was a graduate

student in engineering physics at the Technical University of Delft; from 1953 to 1987 he was a professor

at the same institution.

Curtiss

and

Bird,

Ind.

Eng.

Chm.

Research,

38,2515-2522 (1999); errata,

40,1791

(2001).

s24.2 The Flux Expressions for Heat and Mass

769

Table

24.2-1 Summary1 of Expressions for the

Dmp

in Terms of the

Rp.

[Note: Additional

entries may be generated

cyclic permutation of the indices. Formulas for four-component

systems are given

the references.]

Binary:

Ternary:

systems, the explicit interrelations are given in Tables 24.2-1 and 2. In Eq.

(C)

of Table

24.2-1, it can be seen that for a binary mixture the

Dap

and

Bap

differ by a factor that is a

function of the concentration. However, they do have the same sign, which explains why

the plus sign was chosen in

Eq.

24.2-3 instead of a minus sign.

We are now in a position to present the three final results of this section that are use-

ful as starting points for solving diffusion problems. For

multicomponent

diffusion in gases

liquids,

combining Eqs. 24.1-8 and 24.2-4 gives

This equation has been written in terms of the difference of molecular velocities,

v,+

Equations

(D)

to (I) of Table

17.8-1

may then be used to write this equation in terms of

any desired mass

molar fluxes.

Table

24.2-2 Summary' of Expressions for the

R1,

Terms of the

map.

[Note: Additional

entries can be generated

cyclic permutation of the indices. See the original references for

four-component systems.]

Xlx2

D12D33

D13D23

Ternary:

QI2

W1°2

DI2

IDs3

DI3

[Di23

770

Chapter 24 Other Mechanisms for Mass Transport

If one wishes to designate one species

as being special (for example, the solvent),

then Eq. 24.2-8 can be rewritten thus (see Problem 24C.1):

Note that in

Eq.

24.2-8 there are

N(N

1)/2 symmetric diffusivities, Boa, and that the

Go,

do not appear and are hence not defined. However, in

Eq.

24.2-9, there are

N(N

1)/2 symmetric diffusivities, but the

B,,

of them) now appear, and therefore

we have to supply an auxiliary relation Z,(x,/Bffp)

in which the sum is over all

Equation 24.2-9, with the auxiliary relation, is equivalent to Eq. 24.2-8, and both of these

generalized Maxwell-Stefan equations are equivalent to the generalized Fick equations

of Eq. 24.2-3, together with its auxiliary relation.

For

multicomponent diffusion in gases at low density,

the activity may be replaced by the

mole fraction, and furthermore, to a very good approximation, the

Bop

may be replaced

by 5?hap. These are the

binary

diffusivities for all pairs of species in the mixture. Since the

Bffp vary only slightly with concentration, whereas the

DUp

are highly concentration-

dependent, it is preferable to use the Maxwell-Stefan form (Eq. 24.2-4) rather than the

Fick form (Eq. 24.2-3).

For

binary diffusion in gases or liquids,

Eq.

(C)

of Table 24.2-1 and

Eq.

17B.3-1 may be

used to simplify

Eq.

24.2-8 as follows:

In this equation we have introduced the

thermal difusion ratio,

defined by

(Di/&B)(~A~B/~A~B). Other quantities encountered are the

thermal diffusion factor

and the

Soret coefficient

a,,

defined by

cu,

x,x,

xAxBT. For gases

is almost inde-

pendent of composition, and

is the quantity preferred for liquids. When

is positive,

species

moves toward the colder region, and when it is negative, species

moves toward

the warmer region. Some sample values of

for gases and liquids are given in Table 24.2-3.

For binary mixtures of dilute gases, it is found by experiment that the species with

the larger molecular weight usually goes to the colder region. If the molecular weights

are about equal, then usually the species with the larger diameter moves to the colder re-

gion. In some instances there is a change

the sign of the thermal diffusion ratio as the

temperature is lowered."

In the remainder of the chapter, we explore some of the consequences of the mass-

flux expressions in Eqs. 24.2-8,9, and

10.

EXAMPLE

24.2-1

Thermal

Diffusion

and

the

Clusius-Dickel

In this example we discuss the diffusion of species under the influence of a temperature gra-

dient. To illustrate the phenomenon we consider the system shown in Fig.

24.2-1,

two bulbs

joined together by an insulated tube of small diameter and filled with

mixture of ideal gases

and

The bulbs are maintained at constant temperatures

and

T,,

respectively, and the

Column

diameter of the insulated tube

small enough to eliminate convection currents substantially.

Ultimately the system arrives at a steady state, with gas

enriched at one end of the tube and

depleted at the other. Obtain an expression for

xA2

x,,,

the difference of the mole fractions

at the two ends of the tube.

Chapman and

Cowling,

The

Mathemnticnl

Theory

Non-Uniform

Gases,

3rd

edition,

Cambridge

University

Press

(1970),

274.

s24.2 The Flux Expressions for Heat and Mass

771

SOLUTION

Table

24.2-3 Experimental Thermal Diffusion Ratios

for Liquids and Low-Density Gas Mixtures

Liquids:"

Components A-B

C2H,C14-n-C6H14

C2H,Br2-C2H4C12

C2H2C14-CC14

CBr,-CCl,

CC14-CH30H

CH30H-H20

CYC~O-C~H~~<~H~

Gases:

Components A-B

(K)

~e-~e~

330

0.80

0.40

N2-H2C 264 0.706

0.225

D,-H~~

327

0.90

0.50

0.10

Saxton,

Dougherty, and

Drickamer,

Chem.

Phys., 22,1166-1168 (1954);

Saxton and

Drickamer,

Chem. Phys., 22,1287-1288 (1954);

Tichacek, W.

Kmak, and

Drickamer,

Phys. Chem., 60,660-665 (1956).

Atkins,

Bastick, and

Ibbs,

PYOC. Roy. SOC.

(London), A172,142-158 (1939).

Ibbs,

Grew, and

A. Hirst,

Proc. Roy. Soc.

(London), A173,543-554 (1939).

Heath, T.

Ibbs, and

Wild,

Proc. Roy. SOC.

(London), A178,380-389 (1941).

After steady state has been achieved, there is no net motion of either A or

so that

we take the tube axis to be in the

direction, then from Eq. 24.2-10 we get

Here the activity

has been replaced by the mole fraction xA, as is appropriate for an ideal

gas mixture. Usually the degree of separation in an apparatus of this kind is small.

may

therefore ignore the effect of composition on

and integrate this equation to get

This bulb maintained

at temperature

Fig.

24.2-1. Steady-state binary thermal diffu-

sion in a two-bulb apparatus. The mixture of

gases A and

tends to separate under the in-

fluence of the thermal gradient.

772

Chapter 24 Other Mechanisms for Mass Transport

Because the dependence of

is rather complicated, it is customary to assume

constant

at the value for some mean temperature

T,.

Equation

24.2-12

then gives (approximately)

The recommended5 mean temperature is

Equations 23.2-13 and 14 are useful for estimating the order of magnitude of thermal diffu-

sion effects.

Unless the temperature gradient is very large, the separation will normally be quite

small. Therefore it has been advantageous to combine the thermal diffusion effect with free

convection between two vertical walls, one heated and the other cooled. The heated stream

then ascends, and the cooled one descends. The upward stream will be richer in one of the

components-say, A-and the downward stream will be richer in

This is the principle of

the operation of the

Clusius-Dickel c~lurnn.~~

By coupling many of these columns together in a

"cascade" it is possible to perform

separation. During World War I1 this was one of the

methods used for separating the uranium isotopes by using uranium hexafluoride gas. The

method has also been used with some success in the separation of organic mixtures, where

the components have very nearly the same boiling points, so that distillation is not an option.

The thermal diffusion ratio can also be obtained from the Dufour (diffusion-thermo) ef-

fect, but the analysis of the experiment is fraught with problems and experimental errors dif-

ficult to avoid.9

Next we examine diffusion in the presence of a pressure gradient.

a sufficiently large pres-

sure gradient can be established, then a measurable separation can be effected. One example

Pressure

Diffusion

and

of this is the ultracentrifuge, which has been used to separate enzymes and proteins. In Fig.

the Ultra Centqge

24.2-2 we show a small cylindrical cell in a very high-speed centrifuge. The length of the cell,

and

Fig.

24.2-2.

Steady-state pressure diffusion in a

centrifuge. The mixture in the diffusion cell tends

to separate by virtue of the pressure gradient pro-

in diffusion cell

duced in the centrifuge.

Brown,

Phys.

Rev.,

58,661-662 (1940).

Clusius and

Dickel,

Phys. Chem.,

B44,397450,451473 (1939).

Grew

and

Ibbs,

Thermal Difision in Gases,

Cambridge University Press (1952);

Grew,

Transport Phenomena in Fluids

(H.

Hanley, ed.), Marcel Dekker, New

York

(1969), Chapter 10.

B. Bird,

Advances in Chemical Engineering,

1,155-239 (1956),

9.D.2;

errata,

2,325 (1958).

Chapman and

Cowling,

The Mathematical Theory of Nonuniform Gases,

3rd edition,

Cambridge University Press (19701,

pp.

268-271.

s24.2 The Flux Expressions for Heat and Mass

773

is short with respect to the radius of rotation R,, and the solution density may be consid-

ered a function of composition only. Determine the distribution of the two components at

steady state in terms of their partial molar volumes and the pressure gradient. The latter is

obtained from the equation of motion as

For simplicity, we assume that the partial molar volumes and the activity coefficients are con-

stant over the range of conditions existing in the cell.

At steady state

and the relevant terms in Eq. 24.2-10 give for species

Inserting the appropriate expression for the pressure gradient and then multiplying by

(V5/xA)dz, we get for species

Then we write a similar equation for species

which is

Subtracting Eq. 24.2-18 from Eq. 24.2-17 we get

We now integrate this equation from

to some arbitrary value of

taking account of the

fact that the mole fractions of

and

are

XAO

and xBU, respectively. This gives

is treated as constant over the range of integration, then we get

Then we take the exponential of both sides to find

This describes the steady-state concentration distribution for

binary system in a constant

centrifugal force field. Note that, since this result contains no transport coefficients at all, the

same result can be obtained by an equilibrium thermodynamics analysis." However, if one

wishes to analyze the time-dependent behavior of a centrifugation, then the diffusivity for the

mixing

A-B

will appear in the result, and the problem cannot be solved by equilibrium

thermodynamics.

Guggenheim,

Thermodynamics,

North-Holland, Amsterdam

(1950),

pp.

356-360.

774

Chapter 24 Other Mechanisms for Mass Transport

524.3

CONCENTRATION DIFFUSION

AND

DRIVING

FORCES

In Chapter 17 we wrote Fick's first law by stating that the mass (or molar) flux is propor-

tional to the gradient of the mass (or mole) fraction, as summarized in Table 17.8-2.

On the other hand, in

Eq.

24.2-10 it appears that the thermodynamics of irreversible

processes dictates using the activity gradient as the driving force for concentration diffu-

sion. In this section we show that either the activity gradient or the mass (or mole) frac-

tion gradient driving force may be used, but that each choice requires a different

diffusivity. These two diffusivities are related, and we illustrate this for a binary mixture.

When we drop the pressure-, thermal-, and forced-diffusion terms from Eq. 24.2-10,

we get

This may be rewritten by making use of the fact that the activity coefficient is a function

of xA to obtain

dln

-cgAB(-)

T,P

vxA

The activity may be written as the product of the activity coefficient and the mole frac-

tion (a,

yAxA)

that

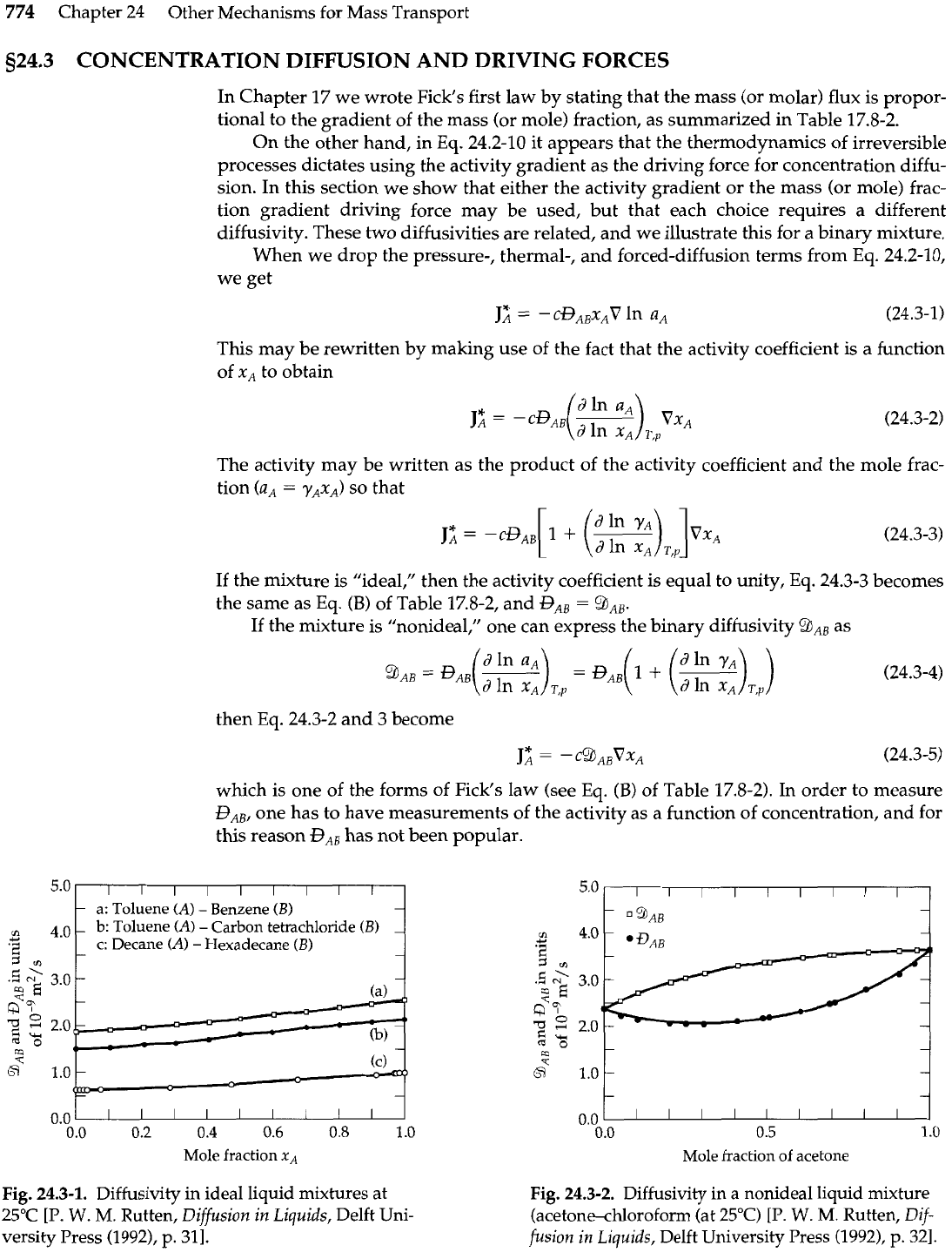
If the mixture is "ideal," then the activity coefficient is equal to unity, Eq. 24.3-3 becomes

the same as

Eq.

(B)

of Table 17.8-2, and

BA,

9,,.

If the mixture is "nonideal," one can express the binary diffusivity

9AB

then Eq. 24.3-2 and 3 become

which is one of the forms of Fick's law (see Eq.

(B)

of Table 17.8-2). In order to measure

B,,,

one has to have measurements of the activity as a function of concentration, and for

this reason

BAB

has not been popular.

a: Toluene (A)

Benzene

(B)

Toluene (A)

Carbon tetrachloride

(B)

c: Decane

(A)

Hexadecane

(B)

0.0

I I

0.0

0.2

0.4

0.6

0.8

Mole fraction

Fig.

24.3-1.

Diffusivity in ideal liquid mixtures at

25°C

[P.

Rutten, Diffusion in Liquids, Delft Uni-

versity Press (1992), p.

311.

Mole fraction of acetone

Fig.

24.3-2.

Diffusivity in a nonideal liquid mixture

(acetone-chloroform (at 25°C) [P.

Rutten,

Dif-

firsion in Liquids, Delft University Press (1992), p. 321.

s24.4 Applications of the Generalized Maxwell-Stefan Equations

775

Fig.

24.3-3.

Effect of activity on the product of viscosity and

diffusivity for liquid mixtures of chloroform and diethyl

1.0

ether

[R.

Powell,

Roseveare, and

Eyring,

Ind.

Mole

fraction

ether

Eng.

Chem.,

33,430435 (194111.

For ideal mixtures

?hAB

and

GAB

are identical, and are nearly linear functions of the

mole fraction as shown in Fig. 24.3-1. For nonideal mixtures

9AB

and

are different

nonlinear functions of the mole fraction; an example is shown in Fig. 24.3-2. However,

the product

pGAB

has been found for some nonideal mixtures to be very nearly linear in

the mole fraction, whereas

/&JAB

is not (see Fig. 24.3-3). There is no compelling reason to

prefer one diffusivity over the other. Most of the diffusivities reported in the literature

are and not

BAB.

924.4

APPLICATIONS OF

THE

GENERALIZED

MAXWELL-STEFAN EQUATIONS

The generalized Maxwell-Stefan equations were given in

Eq.

24.2-4 in terms of the diffu-

sional driving forces d,, and the expression for d, was given in

Eq.

24.1-8. When these

are combined we get the Maxwell-Stefan equations in terms of the activity gradient, the

pressure gradient, and the external forces acting on the various species, given (Eqs. 24.2-

8 or

9):

X,Xfi

(v,

vp)

thermal diffusion terms

n=1

goo

The thermal diffusion terms have not been displayed here, since they will not be needed

in this section. The symbols

m,,

cNl/,

and

designate, respectively, the volume frac-

tion and mass fraction of species

As explained in SS24.1 and 2, several auxiliary rela-

tions have to be kept in mind:

The first of these relations follows from the definition of the d,, the second is a conse-

quence of the Onsager reciprocal relations, and the third is needed because of the intro-

duction of

especially designated species

The choice as to which species is

designated as

is arbitrary; often setting

equal to

is convenient. The choice depends

776

Chapter 24 Other Mechanisms for Mass Transport

on the nature of the system under study, and this point will be illustrated in the exam-

ples that follow.

In all previous chapters, the only external force that has been considered has been

the gravitational force. In this section we set the external force per unit mass

equal to a

sum of forces

Here

is the gravitational acceleration,

is the elementary charge on species

(for ex-

ample, -1 for the chloride ion C1-),

96485

abs.-coulombs/g-equivalent

is the Fara-

day constant,

is the electrostatic potential, and the subscript

on the Kronecker delta

S,,

refers to any mechanically restrained matrix, such as

permselective membrane.

In sum, for solving multicomponent diffusion problems in isothermal systems, we

now have

mass-flux equations (of which only

are independent), the species

equations of continuity, and the equation of motion. This set of equations has proven to

be useful for solving wide classes of mass transfer problems, and we discuss some of

these in the following examples.

Of course, in order to solve multicomponent diffusion problems one needs the

Maxwell-Stefan diffusivities

Bmp

that occur in Eq. 24.4-1. Very few measurements have

been made of these quantities, which require the simultaneous measurement of the ac-

tivity as a function of concentration. Among the few examples of such measurements are

those made by ~utten.'

EXAMPLE

24.4-1

Centrifugation

Proteins

Protein molecules are large enough that they can be concentrated by centrifugation against

the dispersive tendencies of Brownian motion, and this process has proven useful for molecu-

lar weight determination as well as for small-scale preparative separations. Show how the

be-

havior of protein molecules in a centrifugal field can be predicted, and the kind of

information that can be obtained from their behavior in a centrifuge tube (see Fig. 24.4-1).

we shall see in Example 24.4-3, we may treat the protein and its attendant counter-ions as a

single large electrically neutral molecule. Choose the protein as species

and begin with the

mass-flux equation for it. The small ionic species needed for protein stability play no signifi-

cant role in this development and can be ignored.

SOLUTION

We consider here a pseudobinary system of a single globular protein

in a solvent

which

is primarily water, and initially we restrict the discussion to a dilute solution rotating in a

tube perpendicular to the axis of rotation (Fig. 24.,4-la) at a constant angular velocity

For

such a system

and the solute flow field with respect to stationary axes will be that

rigid-body rotation-namely,

6,Ru.

Initial protein

band

y..

.II

Fig.

24.4-1.

Ultracentrifugation of proteins, with two possi-

ble orientations of the centrifuge tube.

Ph.

Rutten,

Diffusion

Liquids,

Delft University Press, Delft, The Netherlands

(1992).