Blum W., Riegler W., Rolandi L. Particle Detection with Drift Chambers

Подождите немного. Документ загружается.

8.4 Limitations Due to Multiple Scattering 309

sum of the large majority of events, which are dominated by small-angle scattering

alone. This behaviour is typical for Coulomb scattering as described by the Ruther-

ford formula; for hadrons, nuclear elastic scattering also makes a contribution to the

tail. All the theories that go beyond the simple approximation discussed above are

analytically quite complex.

Highland [HIG 75] has taken a practical standpoint by ﬁtting the width of the

scattering-angle distribution of the Moliere theory to a form similar to (8.53), using

the radiation lengths as listed in the Particle Data Tables (and partly in our Table 8.6).

He ﬁnds that the width of Moliere does not vary appreciably with the nuclear

charge number Z; he introduces an x-dependent correction factor (1 +

(x))to

(8.53), which redeﬁnes the energy constant. His result is

1/e

14.1MeV



rad



log

rad



. (8.55)

1/e

is the angle in the x–y plane at which the Moliere probability density is down

by a factor of 1/e from the maximum. Formula (8.55) is supposed to be accurate to

5% in the range 10

−3

< x/X

rad

< 10, except for the very light elements, where the

accuracy is 10–20%.

8.4.2 Vertex Determination

At colliders the observation of primary vertices and of secondary vertices from par-

ticles with short lifetimes is through a vacuum tube; in addition there is the material

of the vertex chamber itself. We would like to compute the vertex localization error

due to multiple scattering in these materials. The situation is sketched in Fig. 8.6.

We assume for simplicity that the track is inﬁnitely well measured outside the scat-

tering material. Upon extrapolation, it misses the vertex position by the distance d.

The average over the square of d is equal to

d

 = 

r

+ 

r

+ ··· , (8.56)

where the mean squared projected scattering angle 

 is given by the thickness t

of the layer i in units of radiation lengths of the material i according to (8.53), where



 = 

. We express the r.m.s. value of d in terms of a ‘Coulomb scattering

Fig. 8.6 Coulomb multiple

scattering of an inﬁnitely well

measured track

310 8 Geometrical Track Parameters and Their Errors

limit’ S

of the vertex localization accuracy. By combining (8.56) and (8.53) we

have

d

 =

, (8.57)

with

= 15MeV

∑

1/2

. (8.58)

Practical values of S

range between 45 and 200μm GeV for various experiments;

compare Table 11.3.

The above calculation gives correct vertex errors in the limit that the Coulomb

scattering is much larger than the measurement errors and that all the scattering ma-

terial is between the sense wires and the vertex. For the general case the estimation

of vertex errors is more involved. Although the quadratic addition of measure-

ment errors (8.7) and the multiple-scattering errors (8.57) gives the right order of

magnitude for the total, more sophisticated estimation methods give better results.

Lutz [LUT 88] has developed an optimal tracking procedure by ﬁtting the individual

contributions to multiple scattering between the measuring points.

8.4.3 Resolution of Curvature for Tracks Through

a Scattering Medium

We have seen in (8.53) that the mean square scattering angle increases as the

momentum of the particle becomes smaller. Let us imagine a drift chamber in a

spectrometer where the momentum of a particle is low enough to make the multiple-

scattering error the dominating one. We would like to know the accuracy for a

measurement of the curvature in this situation; this implies we suppose that the ac-

curacy of the apparatus itself is inﬁnitely better than the multiple-scattering errors.

We resume the arguments of Sect. 8.2 at (8.2.1). In order to evaluate [y

] in the

case of multiple scattering, we observe that

]=[y

+(x

−x

)

]=[y

]+(x

−x

)[y

] (8.59)

for x

≥ x

. Now we make use of (8.49) and (8.50) and obtain

(3x

−x

)/12 . (8.60)

Gluckstern [GLU 63] has evaluated the correlation coefﬁcients at the ﬁrst of

N + 1 uniformly spaced wires with the result

]







= −

, (8.61)

8.5 Spectrometer Resolution 311

Table 8.7 Values of the factors C

and E

in (8.61) for various values of N

2 1.33 0.167 0.167

3 1.25 0.125 0.154

4 1.25 0.124 0.160

5 1.26 0.132 0.167

9 1.31 0.156 0.187

inﬁn. 1.43 0.214 0.229







The N-dependent coefﬁcients are listed in Table 8.7.

Let us note that the measurement accuracy

√

] for the curvature in this

multiple-scattering-limited case is inversely proportional to the square-root of the

length. Also, the variations of b and c are much more independent than they were in

the measurement-limited case (8.32), because the ratio D

√

) is relatively

small.

The problem of optimal spacing and optimal weighting has been treated by

Gluckstern [GLU 63] as well as by some other authors cited in his paper.

8.5 Spectrometer Resolution

Much of the effort of constructing precise drift chambers was for the goal of high-

resolution magnetic spectrometers. In this section we want to collect our results

concerning the measurement errors of curvature and to express them in terms of

momentum resolution. We are concerned with measurements inside a homogeneous

magnetic ﬁeld. There were two limiting cases, the one caused by measurement er-

rors, in the absence of multiple scattering, and the other due to multiple scattering,

with zero measurement errors.

8.5.1 Limit of Measurement Errors

We noted before that the variance [c

] of the curvature is a function of the track

length L, the point-measuring accuracy

, and the number N + 1 of wires, but it

does not depend on the curvature itself. For uniform wire spacing we had (8.24)

in Table 8.2)

and for wires with optimum spacing (8.34)

256

N + 1

312 8 Geometrical Track Parameters and Their Errors

The track length is understood to be measured in a plane orthogonal to the magnetic

ﬁeld.

In order to calculate the momentum resolution, we use (8.9) and (8.11) and ex-

press the r.m.s. error

(1/R)=

√

] as

= eB





= −eB

−3



GeV/c



. (8.65)

Introducing

, the angle between the momentum vector and the magnetic ﬁeld, the

transverse component p

is given by

= psin

. (8.66)

We drop the minus sign and write (8.65) as

= psin



GeV/c



] . (8.67)

This formula shows that the spectrometer resolving power, expressed as a percent-

age of the measured momentum, deteriorates proportionally to p. This follows from

the fact that [c

] is independent of c; it is also visible directly in the sagitta s

(Sect. 8.2.3), whose size can be measured with less relative accuracy

s/s as it

shrinks with increasing momentum.

8.5.2 Limit of Multiple Scattering

In this case the variance [c

] depends on the track length L, the mean square scatter-

ing angle per unit length,

, and very weakly on the number of measuring points.

in turn is a function of the scattering material and of the

p of the particle. Using

(8.51) and (8.61) we had for uniform wire spacing

]



21MeV



rad

in Table8.7) . (8.68)

L is the length the track has travelled in the medium and [c

] the variance of

the total curvature. Only a projection on a plane perpendicular to the magnetic

ﬁeld can be confused with a curvature variation caused by a variation in

momentum,

proj

]=[c

]

/sin

, (8.69)

because the projected radius of curvature scales with the square of the projected

length. It is [c

proj

]

to which (8.67) applies in the present case, and we ﬁnd for the

momentum resolution

References 313

sin



GeV/c



]

21(MeV/c)

sin



GeV/c





2LX

rad

(8.70)

We see that the multiple-scattering limit of the momentum resolution is inde-

pendent of momentum because, as p goes up, the decrease in bending power is

compensated by the decrease in the scattering angle. According to (8.70), a muon

traversing 1 m of magnetized iron (2T) at right angles to the ﬁeld cannot be mea-

sured better than to 22%, even if there were inﬁnitely many measuring points with

inﬁnite accuracy inside the iron. Depending on the apparatus, L will often be a func-

tion of the angle

References

[BET 53] H.A. Bethe, Moliere’s theory of multiple scattering, Phys. Rev. 89, 1256 (1953)

[BOC 90] R.K. B

ock, H. Grote, D. Notz, M. Regler, Data analysis techniques for high-energy

physics experiments (Cambridge University Press, Cambridge, UK 1990)

[GLU 63] R.L. Gluckstern, Uncertainties in track momentum and direction due to multiple scat-

tering and measurement errors, Nucl. Instr. Meth. 24, 381 (1963)

[HIG 75] V.L. Highland, Some practical remarks on multiple scattering, Nucl. Instrum. Meth-

ods 129, 497 (1975)

[LUT 88] G. Lutz, Optimum track ﬁtting in the presence of multiple scattering, Nucl. Instrum.

Methods Phys. Res. A 273, 349 (1988)

[MOL 48] G. Moliere, Theorie der Streuung schneller geladener Teilchen II, Mehrfach und

Vielfachstreuung, Z. Naturforsch. 3a, 78 (1948)

[PAR 04] Particle Data Group, Review of Particle Properties, Phys. Lett. B 592 (2004)

[ROS 52] B. Rossi, High-Energy Particles (Prentice-Hall, Englewood Cliffs, NJ, USA 1952)

[SCO 63] W.T. Scott, The theory of small-angle multiple scattering of fast charged particles,

Rev. Mod. Phys. 35, 231 (1963)

[SEL 72] S.M. Selby (ed.), Standard Mathematical Tables (The Chemical Rubber Co.,

Cleveland, Ohio, USA 1972)

[TSA 74] Y.-S. Tsai, Pair production and bremsstrahlung of charged leptons, Rev. Mod. Phys.

46, 815 (1974)

Chapter 9

Ion Gates

Here we wish to take up the subject of ion shutters, which are sometimes placed

in the drift space in order to block the passage of electrons or ions. In Chap. 3 we

introduced such wire grids in the context of the electrostatics of drift chambers,

stressing the relation between the various grids and electrodes that make up a drift

chamber. So far we have dealt with the most straightforward type of gating grid,

where all the wires are at the same potential.

For applications in large drift chambers there are more sophisticated forms of ion

shutters which, in some modes of operation, have different transmission properties

for electrons and for heavy ions.

We will begin this chapter by inspecting the conditions that make it necessary to

involve gating grids (Sect. 9.1). Then we will survey various forms of gating grids

that are in use in particle experiments (Sect. 9.2). Finally we compute values for

the transparency under various conditions for which we make use of the results of

Chap. 2 concerning ion drift velocities and the magnetic drift properties of electrons

in gases.

9.1 Reasons for the Use of Ion Gates

9.1.1 Electric Charge in the Drift Region

Any free charges in the drift volume give rise to electric ﬁelds which superim-

pose themselves on the drift ﬁeld and distort it. Chambers with long drift lengths

L are particularly delicate, especially when they are operated with a low drift ﬁeld.

The displacement

of an electron drift path at its arrival point is of the order

of the drift length times the ratio of the disturbing ﬁeld E

dist

over the drift ﬁeld

drift

= L

dist

drift

. (9.1)

W. Blum et al., Particle Detection with Drift Chambers, 315

doi: 10.1007/978-3-540-76684-1

 Springer-Verlag Berlin Heidelberg 2008

316 9IonGates

This holds if the disturbing ﬁeld is orthogonal to the drift ﬁeld, thus causing a

displacement of the ﬁeld lines to the side, but it also holds if the disturbing ﬁeld

acts in the same direction as the drift ﬁeld, thus causing a change in the velocity and

hence of the arrival time, provided the chamber works in the unsaturated mode of

the drift velocity (cf. Chap. 12).

Free charges can originate as electrons or gas ions from the ionization in the

drift volume, travelling in opposite directions according to their proper drift veloc-

ities, or they can be ions from the wire avalanches that have found their way into

the drift region, where they move towards the negative high-voltage electrode. This

last category contributes the largest part because for every incoming electron which

causes G avalanche ions to be produced at the proportional wire, there will be G

in the drift space, where

is the fraction that arrives in the drift space rather than

on the cathodes opposite the proportional wire. If there is no gating grid, G

will

be of the order of 10

in typical conditions, but could also be larger (see remarks

below).

In order to estimate the size of disturbing ﬁelds we consider two examples. The

ﬁrst is a drift chamber in which a gas discharge burns continuously between some

sense wires and their cathodes. Such a self-sustained process could be caused by

some surface deposit on the cathode, or otherwise. Let the total current be 1μA, and

let

= 5% of it penetrate into the drift volume. If the ion drift velocity there is 2 m/s,

then the linear charge density in the column of travelling ions is

= 25 ×10

−9

s/m. Using Gauss’ theorem in this cylindrical geometry, the resulting radial ﬁeld a

distance r away amounts to

dist

= 450(V)

. (9.2)

Here we have neglected the presence of any conductors.

The second example is the ALEPH TPC, irradiated by some ionizing radiation,

say cosmic rays or background radiation from the e

−

collider. Let the rate density

of electrons liberated in the sensitive volume be R(s

−1

−3

). For every electron, G

ions will appear in the drift space, where they travel with velocity v

. Therefore the

total charge density in the volume has the value.

eRLG

, (9.3)

where e is the charge of the electron and L is the length of the drift volume.

could

depend on the radius r, as one would expect from radiation originating along the

beam. Let the TPC be approximated by the space between two inﬁnite coaxial con-

ducting cylinders with radii r

= 0.3 m and r

= 2 m, with the drift direction parallel

to the common axis. The cylinders are grounded. The radial ﬁeld E

is calculated

from Maxwell’s equations,

∇E

∂

, (9.4)

9.1 Reasons for the Use of Ion Gates 317



dr = 0 .

(r)=

does not depend on r, as in the case of irradiation by cosmic rays, the

resulting radial disturbing ﬁeld takes the form

(r)=



r −

−r

ln(r

)



. (9.5)

If we insert into (9.3) values that are characteristic for the ALEPH TPC irradiated

by cosmic rays at sea level (R = 2×10

−1

−3

, v

= 1.5m/s,G

= 10

,L = 2m),

we ﬁnd that

= 0.43×10

−9

Asm

−3

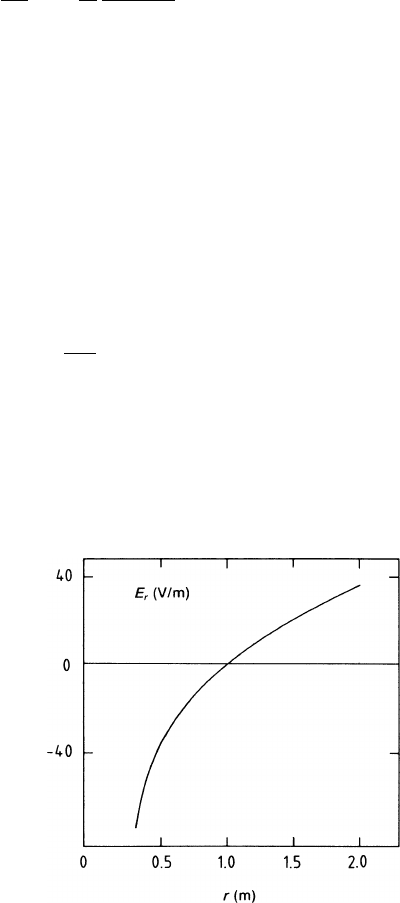
. Figure 9.1 shows the radial ﬁeld that results

from (9.5) in this particular example. We notice that it is negative close to the inner

ﬁeld cage and positive close to the outer one. Compared to the regular axial drift

ﬁeld of 10

V/m, it amounts to a fraction of a per cent.

It should be mentioned that the coefﬁcient

is not very well known. A lower limit

can be evaluated assuming that the ampliﬁcation produced ions uniformly around

the proportional wire. In this case

is equal to the fraction of electric ﬁeld lines that

reach from the sense wire into the drift region. Using the formalism of Sect. 3.2

is equal to the ratio of the surface charge densities on the high-voltage plane and on

the sense wire grid:

, (9.6)

typically between 3 and 5%.

However, it is known that the ampliﬁcation is not isotropic around the propor-

tional wire. This has been discussed in Sect. 4.3. Large avalanches tend to go around

the wire; small avalanches develop on the side where the electrons have arrived. The

ions from the small avalanches may go into the drift space more efﬁciently. Nothing

quantitative has been published concerning this question.

Fig. 9.1 Radial dependence

of the electric ﬁeld produced

by a uniform charge

distribution in a cylindrical

TPC. The scales are from the

example discussed in the text

318 9IonGates

Some further uncertainty exists concerning the value of v

. The effect of charge

transfer between the travelling ions and any gas molecules of low ionization poten-

tial will substitute these molecules, which are often much slower, for the original

ions; see Table 2.2. This effect creates a space charge that is not uniform in the drift

direction.

The most important contribution to space charge is usually created by the back-

ground radiation at the accelerator. Background conditions can be very different

from one experiment to the other. In the ALEPH TPC at LEP (sensitive volume

45m

) the sense-wire current is ∼ 0.5μA under standard operating conditions. The

UA1 central detector at the CERN Sp

pS (sensitive volume 25m

) had a current of

∼ 120μA at the peak luminosity of 3 ×10

−2

−1

[BEI 88].

9.1.2 Ageing

There is experimental evidence of a deterioration in performance of drift and pro-

portional chambers after they have been used for some time. Once the total charge

collected on the anode wires during their lifetime exceeds some value between 10

−4

and 1 C per cm of wire length, a loss of gain and excessive dark currents are observed

in many chambers. Whereas a short account of this problem is given in Sect. 12.6,

we mention it in the context of ion gates in order to underline their effect on the

ageing process.

The dose mentioned above is the product of the incoming charge and the gain

factor. The limit of observable deteriorations depend very much on the gas com-

position and on the electric ﬁeld on the electrode surfaces; under carefully chosen

conditions, a limiting dose of the order of 0.1 to 1 C/cm should be achievable. Some

modern experiments even expect to achieve 10 C/cm (cf. Sect. 12.6). The ageing

process can be stretched in time if only part of the radiation is admitted to the sense

wires, using a gate that is triggered only on interesting events.

9.2 Survey of Field Conﬁgurations and Trigger Modes

In order to describe the various forms of gating grids employed in particle ex-

periments we use two classiﬁcations, one according to drift paths on the basis of

different (electric and magnetic) ﬁeld conﬁgurations, the other according to the dy-

namical behaviour, i.e. how the gates are switched in connection with events in time.

9.2.1 Three Field Conﬁgurations

The simplest gate is the one which has all its wires at the same potential (monopolar

gating grid). We have stated in Sect. 3.3 that it is closed to incoming electrons and

outgoing ions if all the ﬁeld lines terminate on it, provided the common potential is

large enough and positive (Fig. 3.10b).

9.2 Survey of Field Conﬁgurations and Trigger Modes 319

There is a technical difﬁculty connected with this conﬁguration: any transition

from the closed to the open state must occur in a time interval

T comparable to

the electron travel time over a distance small compared to the sensitive drift length,

say

T ≈ 1μs or less. The charge brought onto the grid in this short time causes an

enormous disturbance on the nearby sense wires, orders of magnitudes larger than a

signal. One solution to this problem is the introduction of a ‘shielding grid’ between

the gating grid and the anode [BRY 85].

Another way to circumvent this difﬁculty is to close the gating grid by

ramping two opposite potentials +

and −

on neighbouring wires [BRE 80,

NEM 83]. In this case the net amount of charge on the gating grid does not

change, and in a ﬁrst approximation there is no charge induced in the other elec-

trodes of the drift chamber. This type of grid is called a bipolar gating grid.

In the closed state it has positive charge on every second wire and negative

charge on the wires in between; the drift ﬁeld lines terminate on the positive

charges.

In the presence of a magnetic ﬁeld B the drift paths of electrons are no longer

the electric ﬁeld lines, because their drift-velocity vector has components along B

and along [E ×B] according to (2.6). The exact behaviour is governed by the pa-

rameter

ωτ

, or the ion mobility multiplied by the magnitude of the B ﬁeld. This

parameter is always very small for ions in drift chambers but can be much larger

than one for electrons in suitable gases (cf. Chap. 2). If this is the case and

is increased from zero, the ions are stopped ﬁrst, while many of the electrons are

still able to penetrate. The reason is the reduced electron mobility towards the gat-

ing grid wires. As

is further increased, the gate is ﬁnally closed also for the

electrons.

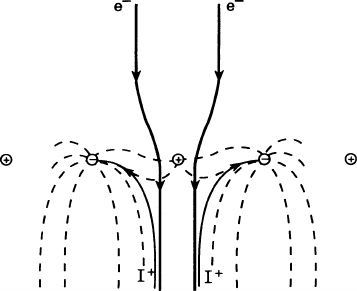
This bipolar gating grid in a magnetic ﬁeld, with a suitable value of

can therefore be operated as a diode ([AME 85-1] and later but independently

[KEN 84]). The electrons from the drift region make their way through the grid on

trajectories which are bent in the wire direction as well as in the direction orthogo-

nal to both the wires and the main drift direction. See Fig. 9.2 for an illustration of

the principle.

Fig. 9.2 Scheme of the

bipolar grid immersed in a

magnetic ﬁeld, which makes

it transparent to electrons

while it remains opaque to

ions