Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений
Подождите немного. Документ загружается.


1
ад
БОЛЬШАКОВ
Ю.ИМАРКУЗЕ
ПРАКТИКУМ
ПО
ТЕОРИИ
МАТЕМАТИЧЕСЮЙ
ОБРАБОТКИ
ГЕОДЕЗИЧЕСКИХ
ИЗМЕРЕНИЙ

Часть I.
ТЕОРИЯ ОШИБОК ИЗМЕРЕНИЙ
Глава 1.
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
§ 1. СОБЫТИЯ И ИХ ВИДЫ. СХЕМА СЛУЧАЕВ
Теория вероятностей — математическая наука, изучающая коли-
чественные закономерности случайных явлений. Случайное
явление — это явление, которое при неоднократном воспроизве-
дении одного и того же опыта, наблюдения протекает каждый раз
несколько по-иному.
Однако в массовом проявлении случайные явления обнаруживают
некоторую закономерность (примерно одинаковое число выпадений
гербов и цифр при бросании монеты, более частое попадание в цент-
ральную часть мишени, чем на ее края, и т. д.).
Результат каждого отдельного наблюдения, опыта, испытания на-
зовем событием (например, при подбрасывании монеты могут проис-
ходить два события: появление герба, появление цифры). События ус-
ловно можно разделить на элементарные, которые нельзя разложить
на более простые, и сложные, состоящие из двух или более элементар-
ных событий (пример: появление положительной ошибки при одном
измерении — элементарное событие, появление пяти положительных
ошибок при 10 измерениях — сложное событие). При выполнении
определенного комплекса условий различают события следующих
видов:
1) достоверные, т. е. такие, которые обязательно происходят (по-
явление герба или цифры при бросании монеты);
2) невозможные, которые никогда не происходят (появление
-
белого
шара при взятии из урны, где лежат только черные шары);
3) несовместные, которые не могут произойти вместе (появление
герба и цифры при одном бросании монеты);
4) совместные, которые могут происходить одновременно (появле-
ние герба и цифры при бросании двух монет);
5) полная группа событий, которую образуют такие события, одно
из которых при испытании обязательно происходит. Полная груп-
па — достоверное событие (например, выпадение одной из граней
при бросании игральной кости);
6) противоположные события — два несовместных события, об-
разующих полную группу;
7) равновозможные события — события, имеющие одинаковую объ-
ективную возможность появления;
8) независимые события — события, имеющие возможность появ-
5
ления, не зависящую от того, появились или не появились другие со-
бытия. Например, выпадение герба в 1-м бросании монеты не зависит
от того, какая ее сторона выпала в предыдущих г—1 бросаниях;
9) зависимые события — такие, у которых эта возможность зави-
сит от того, произошли или не произошли другие события (например,
возможность вынуть один шар из урны, содержащей п шаров, если
уже вынули к шаров и шары обратно не возвращали).
События обычно обозначают заглавными буквами латинского ал-
фавита: А, В, С, ... или А
и
А
2
, ..., А
п
.
Достоверное событие обозначают буквой V, невозможное — бук-
вой V, противоположное по отношению к событию А — через А.
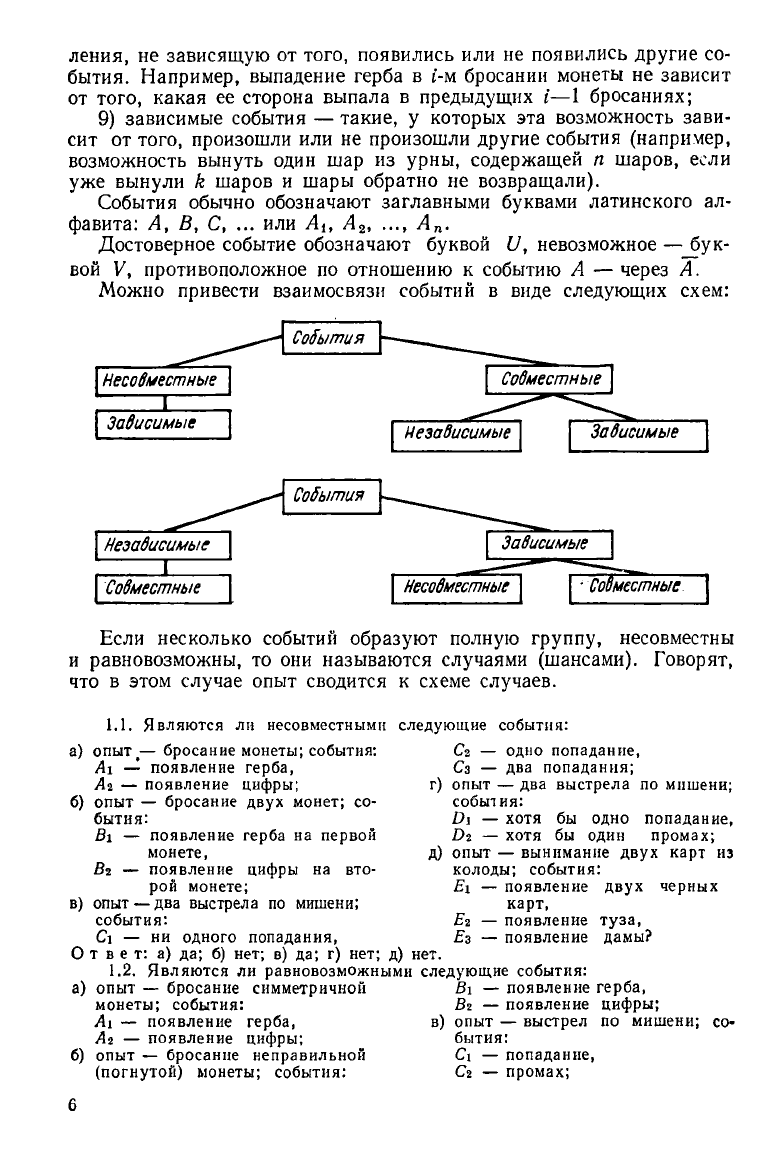
Можно привести взаимосвязи событий в виде следующих схем:
Если несколько событий образуют полную группу, несовместны
и равновозможны, то они называются случаями (шансами). Говорят,
что в этом случае опыт сводится к схеме случаев.
1.1. Являются ли несовместными следующие события:
Сг — одно попадание,
а) опыт.— бросание монеты; события:
А1 — появление герба,
Лг — появление цифры;
б) опыт — бросание двух монет; со-
бытия:
В1 — появление герба на первой
монете,
Вг — появление цифры на вто-
рой монете;
в) опыт — два выстрела по мишени;
события:
Сз — два попадания;
г) опыт — два выстрела по мншени;
события:
1>1 — хотя бы одно попадание,
Г>2 — хотя бы один промах;
д) опыт — вынимание двух карт из
колоды; события:
Е! — появление двух черных
карт,
Еъ — появление туза,
Ез — появление дамы? Сг — ни одного попадания,
Ответ: а) да; б) нет; в) да; г) нет; д) нет.
1.2. Являются ли равновозможными следующие события:
а) опыт — бросание симметричной В\ — появление герба,
монеты; события: Вг — появление цифры;
— появление герба, в) опыт — выстрел по мишени; СО'
Аг — появление цифры; бытия:
б) опыт — бросание неправильной Сг — попадание,
(погнутой) монеты; события: Сг — промах;
6

г) опыт — бросание двух монет; со-
бытия:
Г)\ — появление двух гербов,
Ог — появление двух цифр,
Оз — появление одного герба и
одной цифры;
опыт — вынимание одной карты
из колоды; события:
— появление карты червонной
масти,
О т в е т : а) да; б) нет; в) общем случае нет; г) нет; д) да; е) да.
1.3. Образуют ли полную группу следующие группы событий:
Д)
Ег — появление карты бубновой
масти,
Ез — появление карты трефовой
масти;
е) опыт — бросание игральной кос-
ти; события:
Р1 — появление не менее трех
очков,
Рг — появление не более четы-
рех очков?
собы-
а) опыт — бросание монеты;
тия:
А1 — появление герба,
Аг — появление цифры;
б) опыт — бросание двух монет; со-
бытия:
В1 — появление двух гербов,
Вг — появление двух цифр;
в) опыт — два выстрела по мишени;
события:
Ло — ни одного попадания,
А1 — одно попадание,
Аг — два попадания;
Ответ: а) да; б) нет; в) да; г) да; д) нет.
1.4. Являются ли случаями следующие группы событий:
г) опыт — два выстрела по мишени;
события:
Сх — хотя бы одно попадание,
С% — хотя бы один промах;
д) опыт — вынимание карты из ко-
лоды; события:
— появление карты червон-
ной масти,
йг — появление карты бубновой
масти,
Оз — появление карты трефовой
масти?
а) опыт — бросание монеты; собы-
тия:
Аг — появление герба,
Аг — появление цифры;
б) опыт — бросание двух монет; со-
бытия:
В1 — появление двух гербов,
Вг — появление двух цифр,
Вз — появление одного герба и
одной цифры;
в) опыт — бросание игральной кос-
ти; события:
С1 — появление не более двух
очков,
Сг — появление трех или четы-
рех очков,
не менее пяти
по мишени; со-
С з — появление
очков;
г) опыт — выстрел
бытия:
Ох — попадание,
йг — промах;
д) опыт — два выстрела по мишени;
события:
Е\ — ни одного попадания,
Ег —одно попадание
(
Ез — два попадания;
е) опыт — вынимание двух карт из
колоды; события:
Л — появление двух карт крас-
ной масти,
Рг — появление двух карт черной
масти?
Ответ: а) да; б) нет; в) да; г) нет; д) нет; е) нет.
1.5. Указать, какое событие будет противоположно следующему событию:
а) попадание в цель при одиночном выстреле;
б) поражение цели два раза при трех одиночных выстрелах.
1.6. Привести примеры:
а) трех событий, образующих схему случаев;
б) трех событий, равновозможных и несовместных, но не образующих пол-
ной группы;
в) двух событий, равновозможных и образующих полную группу, но сов-
местных;
г) двух событий, несовместных и образующих полную группу, но не равно-
возможных.
1.7. Зависимы ли следующие события:
а) появление герба или цифры при одном бросании монеты;
б) появление двух или трех очков при одном бросании игральной кости;
в) выпадение герба или цифры при бросании двух монет на каждой из них;
г) появление туза или карты бубновой масти из колоды карт?
Ответ: а) да, б) да; в) нет; г) да.
7

§ 2. КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
С каждым событием связывают понятие вероятности —- числовой
характеристики объективной возможности появления события. Су-
ществуют события, вероятность которых можно определить из усло-
вий самого опыта, не производя его. Для этого необходимо, чтобы
элементарные события составляли схему случаев. Если опыт сводится
к схеме случаев, то вероятность события А можно вычислить по фор-
муле
р(А) = М/ N. (1.1)
где N — общее число случаев, М — число случаев, благоприятству-
ющих появлению событий А. Случай называется благоприятствую-
щим некоторому событию А, если появление этого случая влечет за
собой появление данного события А. Легко видеть, что 0 < р(А) < 1,
причем вероятность достоверного события р(1/) = 1, невозможного
Р(У) = 0.
Определение понятия вероятности на основании формулы (1.1)
называют классическим, а вычисление вероятностей событий по этой
формуле — непосредственным подсчетом вероятностей.
Применяя формулу (1.1), найдем, что вероятность появления герба
при одном бросании монеты р^
р0а
=
1
/
2
. Этому же числу равна ве-
роятность появления положительной (отрицательной) ошибки при од-
ном измерении. Вероятность появления карты бубновой масти при
вынимании одной карты из колоды в 36 листов
Рбубн. масти = 9/36 =1/4.
Вероятность выпадения грани с цифрой 6 при одном бросании иг-
ральной кости р
в
= 7
е
.
1.8. Из тщательно перемешанной колоды карт в 36 листов вынимается на-
удачу одна карта. Определить вероятность появления: а) пиковой дамы, б) коро-
ля, в") карты бубновой масти, г) карты черной масти.
Ответ: а, 1/36; б) 1/9; в) 1/4; г) 1/2.
1.9. Слово «геодезия» составлено из отдельных букв, написанных на одина-
ковых карточках. Карточки перевернуты и перемешаны. Найти вероятность то-
го, что, взяв наудачу одну из них, откроют карточку с написанной на ней:
1) буквой «г», 2) гласной буквой, 3) буквой те«.
Ответ: 1) 1/8; 2) 5/8; 3; 2,8.
1.10. Из колоды карт в 52 листа вынимают наугад 10 карт. Затем наудачу
одну из вынутых карт открывают. Найти вероятность того, что вскроется туз.
Ответ: 1/13.
1.11. Цифры 1, 2, 3, 4, 5 написаны каждая на отдельной карточке. Все кар-
точки одинаковы. Тщательно перемешав карточки, берут наугад две подряд. Ка-
кова вероятность, что поставленное из этих цифр в порядке их появления число
будет четным?
Ответ: 2/5.
1.12. В урне находится 5 красных, 7 зеленых и 8 белых шаров. Все шары по
размерам и массе одинаковы. Шары тщательно перемешиваю- и наугад вынима-
ют один шар. Определить вероятность того, что вынутый шар будет: а) красным,
б) зеленым, в) белым, г) цветным.
Ответ: а) 1/4; б) 7/20; в) 2/5; г) 3/5.
1.13. Определить вероятность того, что при двух измерениях появится одна
положительная ошибка.
8

Решение. Чнсло всевозможных случаев N = 4: 1) две положительные
ошибки, 2) положительная и отрицательная ошибка, 3) отрицательная и положи-
тельная ошибка, 4) две отрицательные ошибки. Число благоприятных случаев
М = 2. Следовательно, р = 2/4 = 1/2.
Замечание. Известна ошибка Даламбера, который не различал вторую
и третью комбинации и принимал М = 3 (в аналогичной задаче с подбрасывани-
ем одной монеты).
1.14. В записанном номере телефона оказалась стертой последняя цифра.
Какова вероятность того, что, наугад набирая последнюю цифру телефонного
номера, можно сразу позвонить нужному лицу?
Ответ: 1/10.
1.15. Найти вероятность того, что при бросании двух игральных костей
сумма очков окажется равной: 1) четырем, 2) пяти, 3) шести, 4) семи, 5) восьми,
6) девяти, 7) десяти, 8) одиннадцати, 9) двенадцати, 10) двум.
Ответ: 1) 1/12; 2) 1/9; 3) 5/36; 4) 1/6; 5) 5/36; 6) 1/9; 7) 1/12; 8) 1/18; 9) 1/36;
10) 1/36.
1.16. В урне а белых и Ь черных шаров. Из урны наугад вынимают один шар.
Найти вероятность того, что этот шар — белый.
Ответ: а/(а + Ь).
1.17. В урне а белых и Ь черных шаров. Из урны вынимают один шар и от-
кладывают в сторону. Он оказался белым. После этого из урны берут еще один
шар. Найти вероятность того, что и этот шар белый.
О т в е т: а — 1/(а + Ь — I).
1.18. Из урны, в которой а белых и Ь черных шаров, вынимают подряд все
находящиеся в ней шары. Найти вероятность того, что вторым по порядку будет
вынут белый шар, черный шар, пятый шар будет белым (а > 5).
Ответ: аЦа + Ь), Ы(а + Ь). а/(а + Ь).
Для решения более сложных задач необходимы некоторые сведения
из комбинаторной математики. Приведем их. Существуют следующие
виды комбинаций из п элементов а, Ь, с, ...
1. Перестановки — такие комбинации из п элементов, которые раз-
личаются лишь порядком расположения в них элементов. Число пере-
становок определяется формулой р
п
= п\
2. Размещения из п элементов по к элементов — такие комбина-
ции, которые различаются как порядком элементов, так и самими
элементами; например, размещениями из трех элементов а, Ъ, с по
два будут
(аЬу, (ас); (Ьс)\
(Ьа); (са); (сЬ).
Их чнсло Ап — пМ(п — 6)!
3. Сочетания из п элементов по к элементов — такие комбинации,
которые различаются только самими элементами; например, сочета-
ниями из трех элементов а, Ь, с по два будут аЬ, Ьс и ас. Их число
Сп = п \/{п — к)
I
к\,
при этом имеют место свойства:
С
О РЛ 1 . (Л I У-./—К РА
Решим несколько типовых задач.
1.19. На четырех карточках написаны буквы: «с», «т», «о», «л». Карточки пе-
ремешивают, вынимают наугад по одной, раскладывая их в порядке появле»
ния. Найти вероятность того, что составится слово «стол».
9

Решение. Так как число благоприятствующих случаев М — 1, а число
всех случаев Л' = р
4
= 4!, то искомая вероятность р
стол
= 1/4! = 1/24.
1.20. В условиях задачи 1.19 найти вероятность составления слова «лот», ес-
ли вынимать три карточки.
Решение. Число благоприятствующих случаев М — 1, число всех
случаев N = А*. Поэтому р
лот
=
М
А\ = 1/4! = 1/24.
1.21. В условиях задач (1.19) и (1.20) найти вероятность появления того же
слова, если карточки разрешается раскладывать не в порядке их появления.
Решен и е. Так как порядок расположения элементов здесь безразличен,
то мы имеем число всех случаев N = С\- Поэтому
_ _!_ _ (4-3)131 _ 1
Рл<п
с* ~ 4
1
~ 4 '
1.22. Определить вероятность того, что наугад расставленные на шахматной
доске 8 ладей не будут бить друг друга.
Решение. Число всех способов, которыми можно расставить ладьи на
шахматной доске, равно С
6
® (если бы это были не ладьи, а 8 различных фигур,
то число способов было бы равно <4
6
®). Число благоприятствующих случаев, оче-
видно, равно р
в
— 8! Поэтому искомая вероятность
р = -±1- =
8
'
56
1
8 !
= (
8|
>
2
=
9 ! . ,0-е
с? 64
I
64 • 63 ... 57
04
1.23. В урие а белых и Ь черных шаров. Из урны вынимают два шара. Най-
ти вероятность того, что оба шара будут белые.
Ответ: р = С
2
а
1С?
+ ь
.
1.24. Найти вероятность того, что, вынимая из колоды карт в 52 листа три
карты, получим раскладку: «тройка, семерка, туз».
Решение. Число всех случаев будет равно N = число благоприят-
ствующих случаев М = С\ • С\ • С\ = 4
3
. Поэтому р(А) = 4
3
//4|
2
; если бы
порядок расположения карт был безразличен, то тогда р(А) = 4
3
1С1
2
0,0029.
Часто встречаются еще следующие виды комбинаций.
Перестановки с повторениями — такие комбина-
ции из п элементов, среди которых имеется п
г
(»' = 1,2, ... к) элемен-
тов к видов. Их число
п
г
,...п
к
) =
1, \п
2
! ... п
к
!
1.25. На карточках написаны буквы: «з», «а», «к», «а», «з». Найти вероят-
ность того, что, вынимая наугад по одной из карточек и раскладывая их в поряд-
ке появления, получим слово «заказ».
511
Ответ! п„
якя
„ = 1 ; = — .
2 12! 1! 30
Размещения с повторениями — комбинации из
элементов 5 видов по к. Их число А% = 5*.
1.26. Производят три измерения. Найти вероятность того, что эти измерения
будут содержать две положительные ошибки.
<
10

Решение. Число благоприятствующих случаев М = С3, число всех случа-
ев А/ = А\ = 2
3
= 8. Поэтому р = С|/2
3
= 3/8.
1.27. В условиях задачи 1.19 найти вероятность появления слова «лот», если
карточки возвращаются обратно. ^
Решение. Число благоприятствующих случаев составит N = А^ = 4®.
Поэтому Рлот =
1
/4
3
.
1.28. Состоящее из пяти букв «тайное слово» секретного замка набира-
ется с помощью одного диска, на котором нанесено 10 букв. Чему равна вероят-
ность открыть замок с первой попытки человеком, не знающим этого слова.
Решение. Так как число благоприятствующих случаев М = 1, а число
всех случаев равно N = то искомая вероятность р= 1М®
0
= 1/10
5
=
= 0,00001.
1.29. В урне находятся 10 шаров: 3 красных н 7 синих. Найти вероятность
того, что, вынимая одновременно 2 шара, достанут оба синих.
Решение. Число всех равновозможных случаев вынуть пары шаров опре-
деляется числом сочетаний из 10 по 2, т. е. п = С?
0
= 10 • 9/1 • 2 = 45.
Чнсло благоприятствующих случаев определяется числом сочетаний из 7
синих шаров по два т = 7 • 6/1 • 2 = 21.
Следовательно, р = 21/45 = 7/15 = 0,467.
1.30. Из тщательно перетасованной колоды карт в 36 листов вынимают одно-
временно две карты. Определить вероятность появления: а) дамы и короля треф,
б) дамы и короля любой одной масти, в) дамы и короля разных мастей.
Ответ: а) 1/630; б) 2/315; в) 2/105.
1.31. В урне находится 5 шаров: 2 красных и 3 синих.Какова вероятность
того, что, вынимая сразу 2 шара, достанут оба красных?
Ответ : 1/10.
1.32. Каждая из букв «в», «я», «н», «е», «к», «а», «з» написана на отдельной
карточке. Карточки перемешивают, вынимают наугад по одной и раскладывают
в порядке их появления. Определить вероятность того, что составится слово
«невязка».
Ответ: 1/5040.
1.33. По условиям задачи 1.32 найти вероятность того, что из первых трех
карточек составится слово «век».
Ответ: 1/210.
Те же условия, но карточки разрешается раскладывать не обязательное по-
рядке их появления.
Ответ: 1/35.
1.34. В урне а белых и Ь черных шаров (а 2). Из урны вынимают сразу
два шара. Найти вероятность того, что оба шара будут белыми.
Решение. Общее число случаев
„ _ „2 _ (д + *)(я-Н-1)
-
С
а+Ь ~ , .
2
Число благоприятных случаев М = а(а — 1)/1 • 2.
Вероятность события А (два белых шара) равна
р(Л) =
^
=
М^о
N (
а
+Ь)(а+Ь-\)
1.35. В партии, состоящей из к изделий, имеется / дефектных. Из партии вы-
бирается для контроля г изделий. Найти вероятность р того, что из них ров-
но 5 изделий будут дефектными.
Ответ: р= С^С^/С^.
1.36. Найти вероятность выигрыша в спортлото (угадать к = 4, 5 или 6 но-
меров, если из 49 номеров в карточке зачеркивать 6 номеров).
От ве т: р = С* С
6
^*/^.
и

1.37. Из урны, содержащей п перенумерованных шаров, наугад вынимают
один за другим все находящиеся в ней шары. Найти вероятность того, что номе-
ра вынутых шаров будут идти по порядку: 1, 2, ..., п.
Ответ: 1/л!
1.38. Та же урна, что и в предыдущей задаче, но каждый шар после выни-
мания вкладывается обратно и перемешивается с другими, а его номер записы-
вается. Найти вероятность того, что будет записана естественная последователь-
ность номеров: 1, 2 п.
Ответ: 1/п".
1.39. Полная колода карт (52 листа) делится наугад на две равные пачки по
26 листов. Найти вероятности следующих событий:
А — в каждой из пачек окажется по два туза;
В — в одной из пачек не будет ни одного туза, а в другой — все четыре;
С — в одной из пачек будет один туз, а в другой — три.
Решение. Общее число случаев п = С^. Число благоприятных собы-
тию А случаев т — С^С^
р(А) = С\ С\У С?^ = 0,390.
Событие В может осуществиться двумя способами: либо в первой пачке будут все
четыре туза, а во второй — ни одного, либо наоборот
р (В) = 2С^С=|СЦ/С|| = 0,1Ю.
Аналогично
р(С) = 2СЗС^/С?® = 0,499.
1.40. На пяти карточках написаны цифры 1, 2, 3, 4, 5. Две из них, одну
за другой, вынимают. Найти вероятность того, что число на второй карточке бу-
дет больше, чем на первой.
Решение. Опыт имеет два возможных исхода:
А — второе число больше первого,
В — второе число меньше первого.
Так как условия опыта симметричны относительно А и В, то р = 1/2.
1.41. Тот же вопрос, что и в задаче 1.40, но первая карточка кладется обрат-
но и смешивается с остальными, а стоящее на ней число записывается.
Решение. Возможно три исхода:
А — второе число больше первого,
В — второе число меньше первого,
С — второе число равно первому.
Всего возможно А| = 25 случаев; из них пять
1,1; 2,2; ...; 5,5
благоприятны событию С, а остальные 20 поровну делятся на благоприятные со-
бытиям А и В. Поэтому р(А) = р(В) = 10/25 = 2/5.
1.42. N человек случайным образом рассаживаются за круглым столом
(,У>2). Найти вероятность р того, что два фиксированных лица окажутся рядом.
Решение. Число случаев п = N1, число благоприятных случаев т —
= 2Ы, так как всего пар соседних мест /V, а на каждой паре соседних мест лиц
А и В можно рассадить двумя способами:
р = 2Л7ЛЧ =2/(ЛГ— 1)1
1.43. Та же задача, но стол прямоугольный, и N человек рассаживаются
случайно вдоль одной из его сторон.
Ответ: р = 2(Ы — 1)/ЛЧ
1.44. В урне находится 5 красных, 3 синих и 2 зеленых шара. Перемешав
их, вынимают 2 шара. Какова вероятность, что оба вынутых шара будут одного
цвета.
12

Ответ: [С\ + С\ + С|)/С?
0
= 14/45.
1.45. Наудачу взятый телефонный номер состоит из 5 цифр. Найти вероят-
ность, что в нем: 1) все цифры различные; 2) все цифры нечетные, 3) все цифры
кратны трем.
Ответ: 1. р -== 0.3024;
4о 10»
I 1 \
8
2. р=
=7
-= — =0,03125; 3. р = 0,00243.
К 2
'
1.46. Измеряют угол между направлениями на две марки А и В. На марку А
видимость постоянная. Видимость на марку В периодически закрывается прохо-
дящим поездом, при этом промежутки видимости и невидимости одинаковы и сос-
тавляют 3 мин. Время визирования на каждую мерку с выполнением необходимых
отсчетов составляет 1 мин. Какова вероятность того, что, визируя в произвольный
момент времени первоначально на марку А, наблюдатель завершит измерение
угла до закрытия видимости на марку В.
Ответ: 1/3.
§ 3. ОТНОСИТЕЛЬНАЯ ЧАСТОТА (ЧАСТОСТЬ) И ВЕРОЯТНОСТЬ
Очевидно, не всякий опыт может быть сведен к схеме случаев, и
поэтому существуют события, вероятности которых невозможно вы-
числить по формуле (1.1), например, вероятность сбить самолет одним
выстрелом, вероятность выпадения герба, если монета не имеет пра-
вильной формы, вероятность появления той или иной игральной карты,
если игра нечестная, и т. д. Для таких событий применяют другие спо-
собы определения вероятностей. Все эти способы связаны с опытом
(экспериментом) и понятием относительной частоты (частости) со-
бытия.
Относительной частотой события называют
отношение числа появлений этого события т к числу всех произве-
денных опытов п, т. е.
(2 = т/п. (1.2)
При неограниченном числе опытов с вероятностью, сколь угодно
близкой к единице, можно ожидать, что относительная частота собы-
тия приближается к его вероятности (теорема Бернулли), т. е.
верНт(2 = р. (1.3)
Вероятный предел (вер Пт) отличается от математического пре-
П-* оо
дела и понимается как тенденция стремления к пределу. Выражение
(1.3) пишут также в виде р{\(,}—р| •< е} = 1 — б, где е и 6 — сколь
П-Юо
угодно малые положительные величины.
Относительную частоту называют также статистической вероят-
ностью события.
1.47. Из 5000 взятых наудачу деталей оказалось 32 бракованных. Найти
частость бракованных деталей в данной партии.
13
