Бондаренко В.В. Основы теории цепей. Часть 2
Подождите немного. Документ загружается.

61
Это задача анализа. В отличие от этого, задача синтеза: знаем
a(p), a(t), желаем получить b(p), b(t). Она решается неоднознач-
но, в отличие от задачи анализа.
x(p) может быть и ток, и напряжение — нас пока это не интере-
сует.
(
)
=
(
)
( )
,
(
)
=
(
)
( )
,
(
)
=
(
)
(
)
экв
(
)
=
(
)
(
)
=
(
)
(
)
⋅
(
)
(
)
⋅
(
)
(
)
=
(
)
⋅
(
)
⋅
(
)
§2.11. СВЯЗЬ МЕЖДУ ОПЕРАТОРНОЙ ПЕРЕДАТОЧНОЙ
ФУНКЦИЕЙ И КОМПЛЕКСНЫМ КОЭФФИЦИЕНТОМ ПЕРЕДАЧИ
(
)
=
(
)
(
)
=
+
+ ⋯+
+
+ ⋯+
Если мы формально подставим = , мы получим комплекс-
ный коэффициент передачи.
(
)
=
(
)
(
)
=
(
)
+
(
)
+ ⋯+
(
)
+
(
)
+ ⋯+
=
+
+
=
= + =
(
)
⋅
(
)
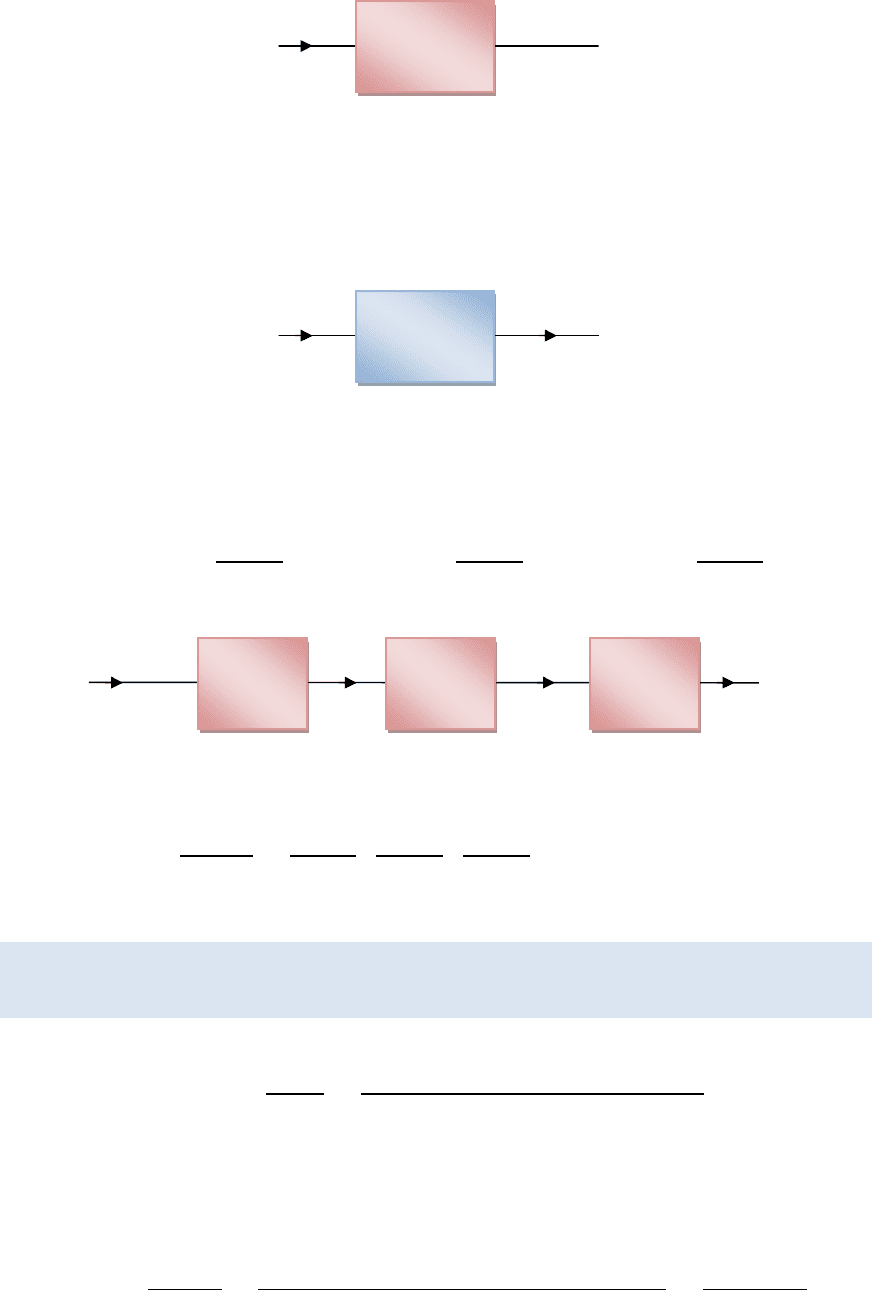
H
1
(p)
x
1
(p)
H
2
(p) H
3
(p)
x
2
(p) x
3
(p) x
4
(p)
?
a(p) b(p)
a(t) b(t)
H(p)
a(p) ?
62
(
)
=
|
(
)
|
= √
+
— амплитудно-частотная характери-
стика.
Ψ
(
)
=arctg
— фазо-частотная характеристика.
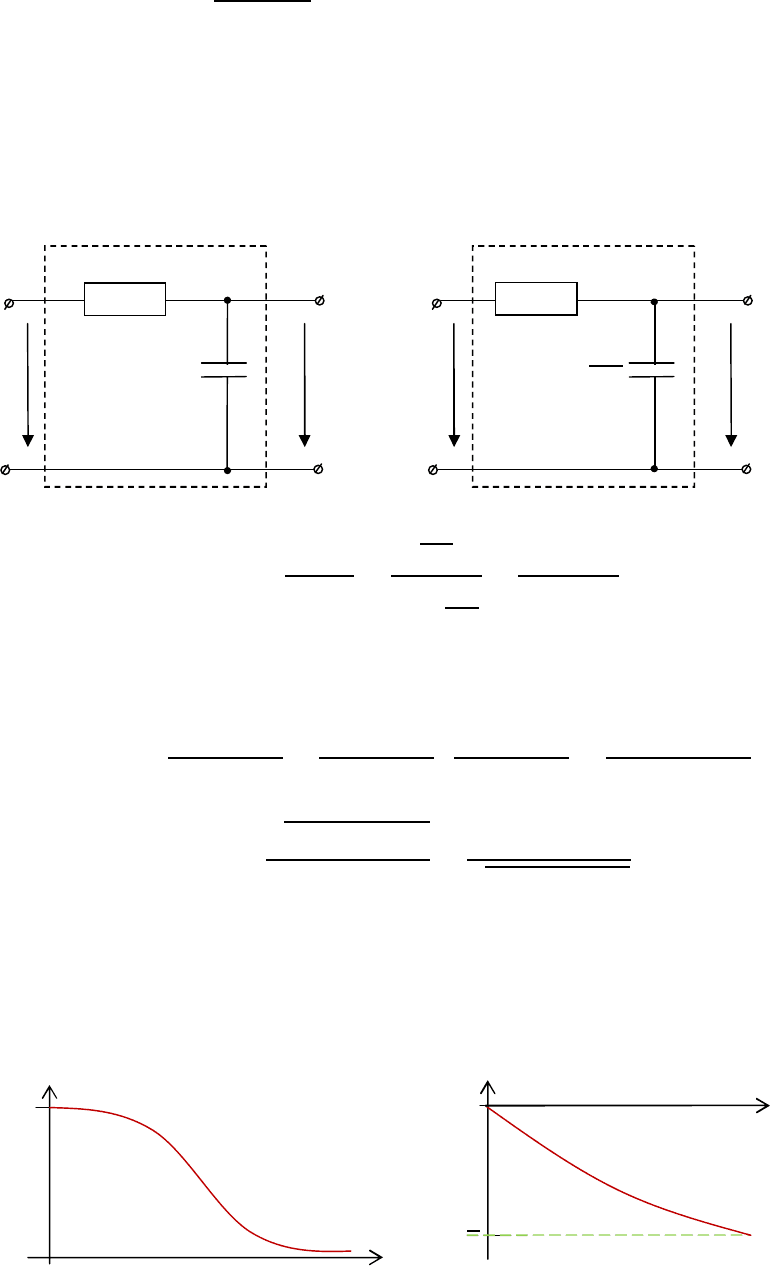
Пример.
(
)
=
(
)
(
)
=
1
+
1
=
1
+1
Комплексный коэффициент передачи:
(
)
=
1
1+
=
1
1+
⋅
1 −
1 −
=
(
1 −
)
1+
(
)
=
√1+
1+
=
1
√1+
— амплитудно-частотная характеристика.
Ψ
(
)
=arctg (− ) — фазо-частотная характеристика.
При формальном подставлении вместо jω мы переходим к сим-
волическому методу от операторной функции.
ω
ψ(
ω
)
0
−
ω
H(jω)
1
1
(
)
(
)
R
C
R
63
Глава 3. Анализ электрических
цепей при произвольном входном
сигнале
a(t) — произвольный входной сигнал.
Разбиваем его на a
1
(t), a
2
(t), …, a
k
(t).
Ищем реакцию на каждый элемен-
тарный сигнал b
1
(t), b
2
(t), …, b
k
(t).
Общая реакция будет равна сумме отдельных реакций цепи.
(
)
=
(
)
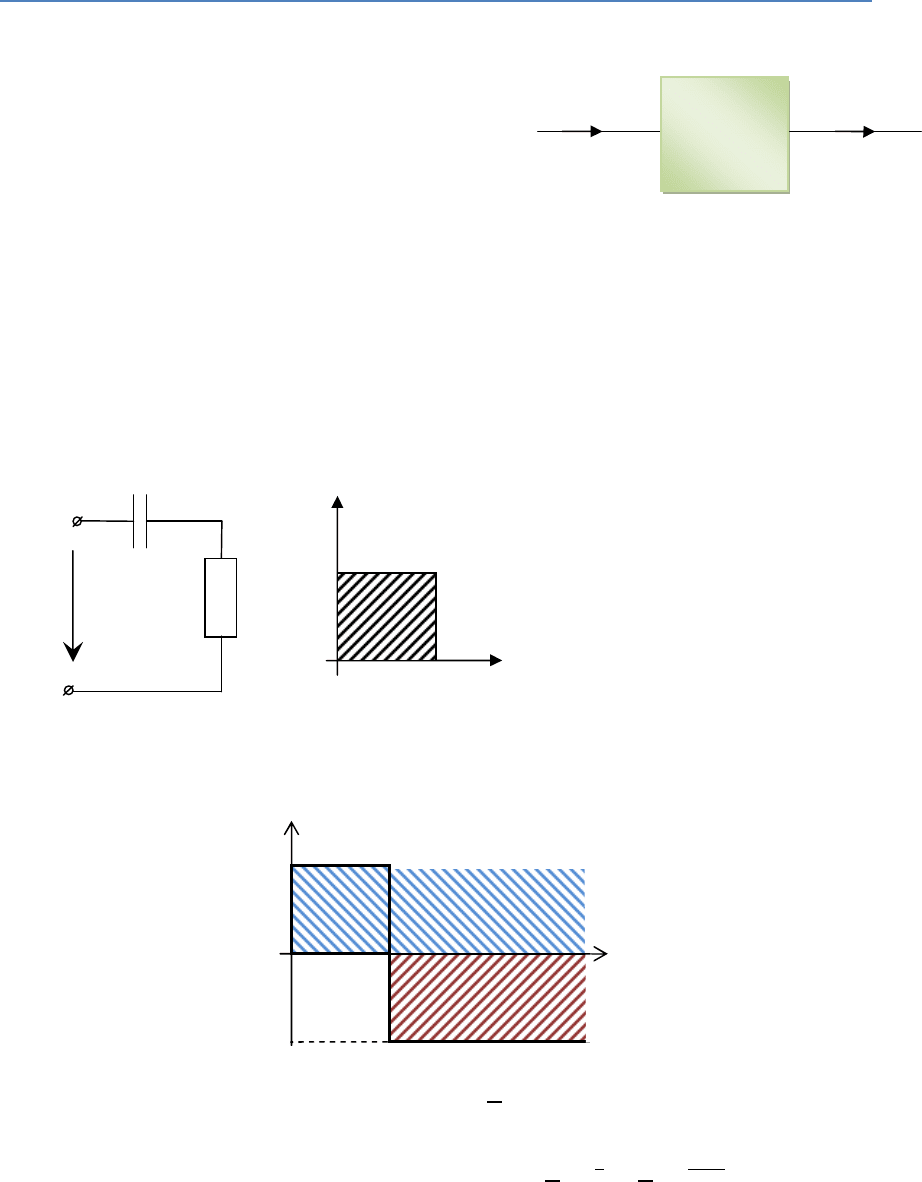
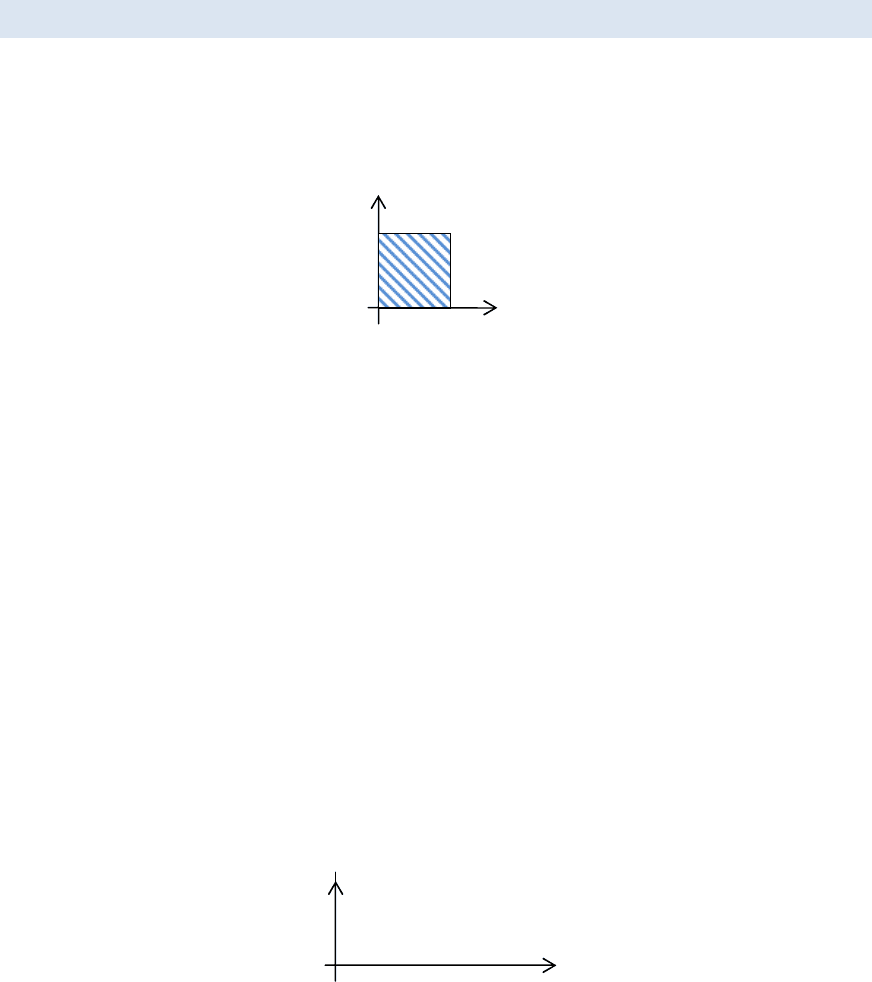
Прямоугольный им-
пульс. Начальные ус-
ловия нулевые.
,
—————————
(
)
=
Представим этот сигнал в виде двух элементарных сигналов.
На первом интервале 0 ≤ ≤
, =
⁄
.
На втором интервале
≤ =
+
=
−
.
t
u
U
t
1
–
U
t
t
u
U
t
1
R
C
u(t)
ЭЦ
a(t) b(t)
найти
64
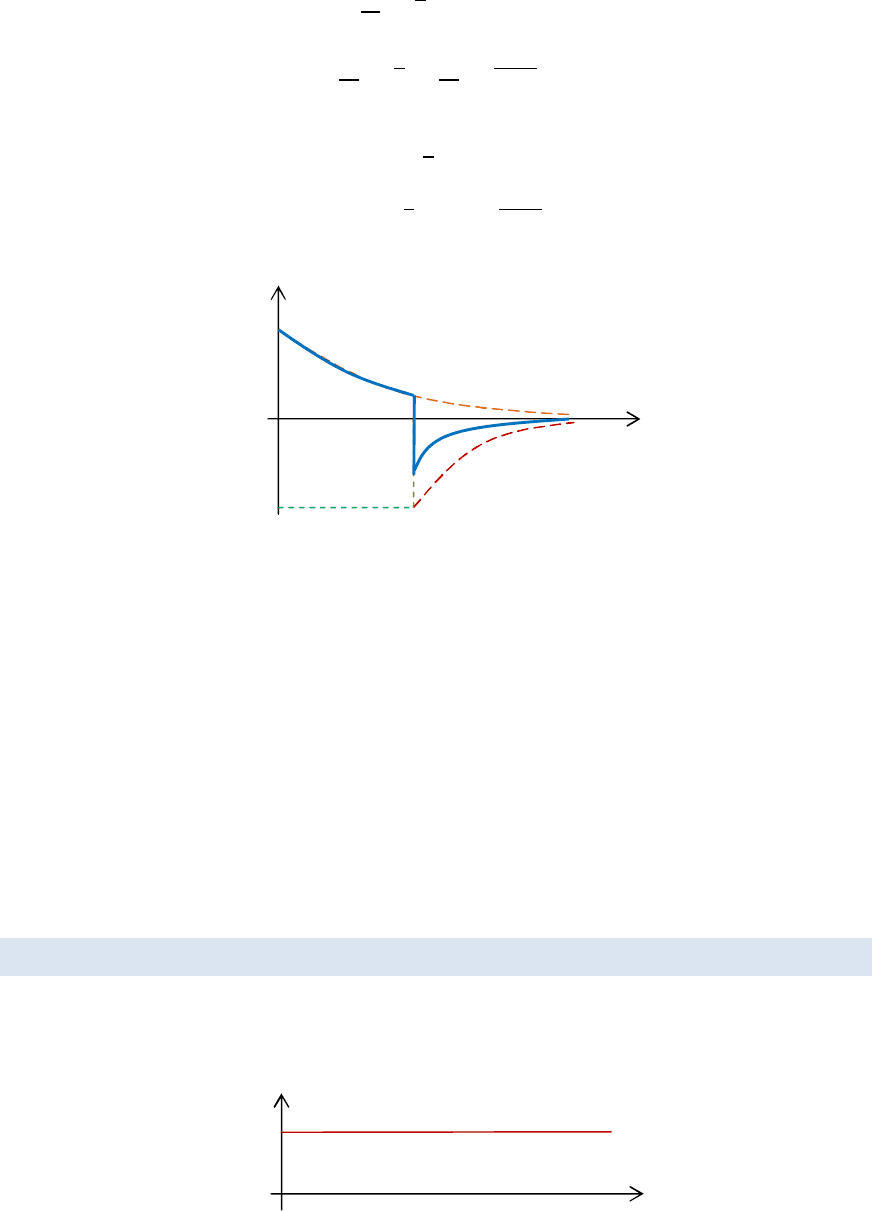
(
)
=
, 0 ≤ ≤
−
,
≤
(
)
=
, 0 ≤ ≤
−
,
≤
Как видим, на входе прямоугольный импульс, на выходе уже
непрямоугольный, то есть присутствуют искажения.
Выводы:
1) Теория переходных процессов позволяет нам перейти к рас-
чёту реакции цепи при произвольном входном сигнале.
2) Такими элементарными функциями являются единичная
функция и импульсная функция.
§3.1. ЕДИНИЧНАЯ ФУНКЦИЯ
(ЕФ, 1(t), функция Хэвисайда)
То есть это ступенька величиной 1.
1
(
)
=
0, <0
1, ≥ 0
1(t)
t
1
0
u
R
t
U
t
1
– U
65
Она может быть сдвинута по времени.
1
(
−
)
=
0, <
1, ≥
Если ступенька в k раз больше, то такой сигнал называется
сигналом включения.
§3.2. ИМПУЛЬСНАЯ ФУНКЦИЯ
(
(
)
, функция Дирака).
Единичный импульс:
⋅ =1
Единичным импульсом называется импульс прямоугольной
формы, интенсивность которого, или площадь, равна единице.
Увеличивая амплитуду до бесконечности и уменьшая длитель-
ность до нуля, получаем импульсную функцию.
(
)
=1
(
)
=
0, ≠ 0
∞, =0
(
−
)
=
0, ≠
∞, =
δ(t)
t
0
t
A
τ

66
Найдём связь между импульсной функцией и единичной
функцией.
(
)
=1=1
(
)
(
)
=
1( )
Если интенсивность не единица, а в k раз больше, такой сигнал
( ) называется импульсом воздействия.
(
)
=
(
)
[В]
[А]
§3.3. ПЕРЕХОДНАЯ ХАРАКТЕРИСТИКА ЦЕПИ
(
)
= 1( )
ℎ
(
)
=
(
)
( )
|
н.н.у.
=
(
)
1( )
|
н.н.у.
Переходной характеристикой цепи ℎ
(
)
называется отно-
шение реакции цепи b(t) к сигналу включения a(t) при нулевых
начальных условиях.
ℎ
(
−
)
=
(
−
)
( −
)
|
н.н.у.
=
(
−1
)
1( −1)
|
н.н.у.
1) Переходная характеристика цепи — это фактически реакция
цепи на функцию Хэвисайда.
ЭЦ
a(t)
b(t)
воздействие
реакция
δ(t–t
1
)
t
t
1
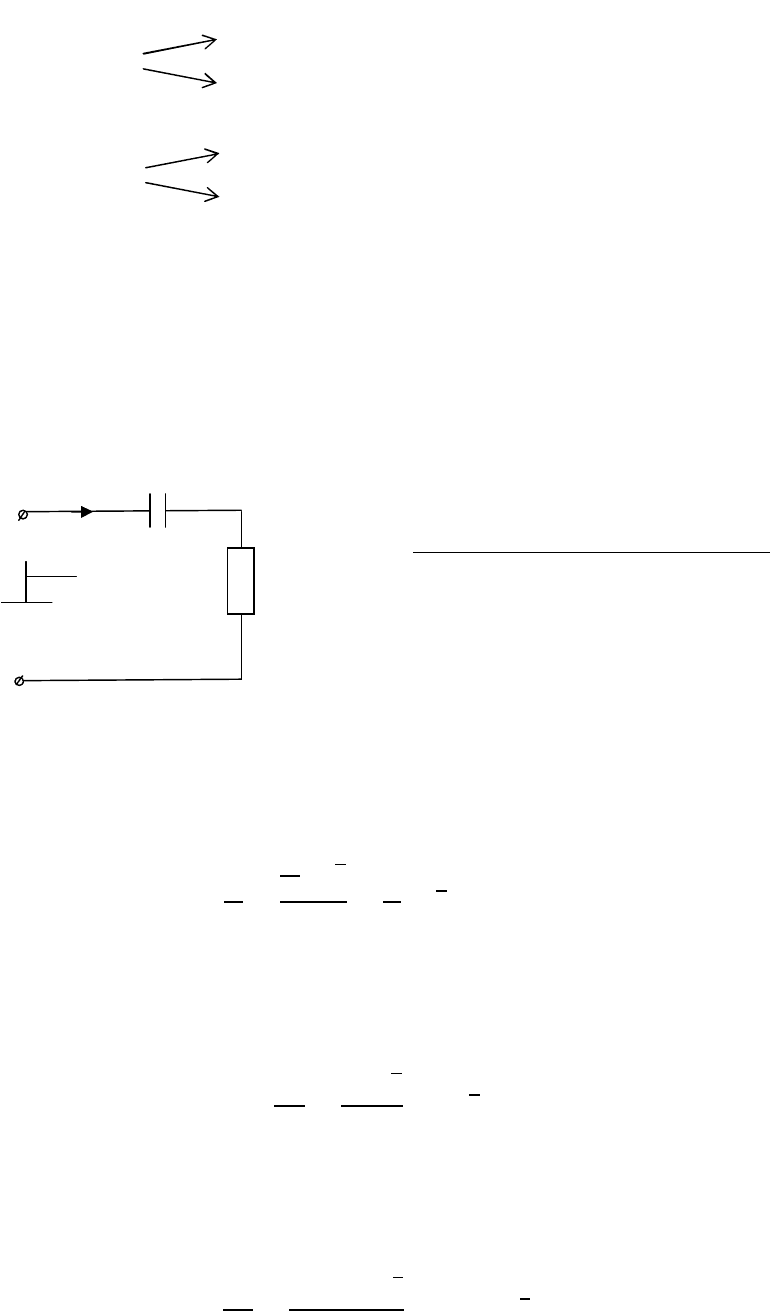
67
2) Размерность:
3) Переходную характеристику цепи можно рассчитать класси-
ческим или операторным методом как реакцию на ступеньку в
1 В или ступеньку в 1 А.
Пример.
,
,
н. у. — нулевые
ℎ
(
)
Подключим постоянное напряжение величиной U. Начальные
условия нулевые. Определить переходную характеристику по
току для данной схемы.
ℎ
(
)
=
=
=
1
Ом
Найдём переходную характеристику по напряжению на эле-
менте R.
ℎ
(
)
=
=
=
Найдём переходную характеристику по напряжению на эле-
менте С.
ℎ
(
)
=
=
−
=1−
R
U
C
i
U
I
u →
безразмерная
i → [Ом
-1
]
u → [Ом]
i → безразмерная
на входе
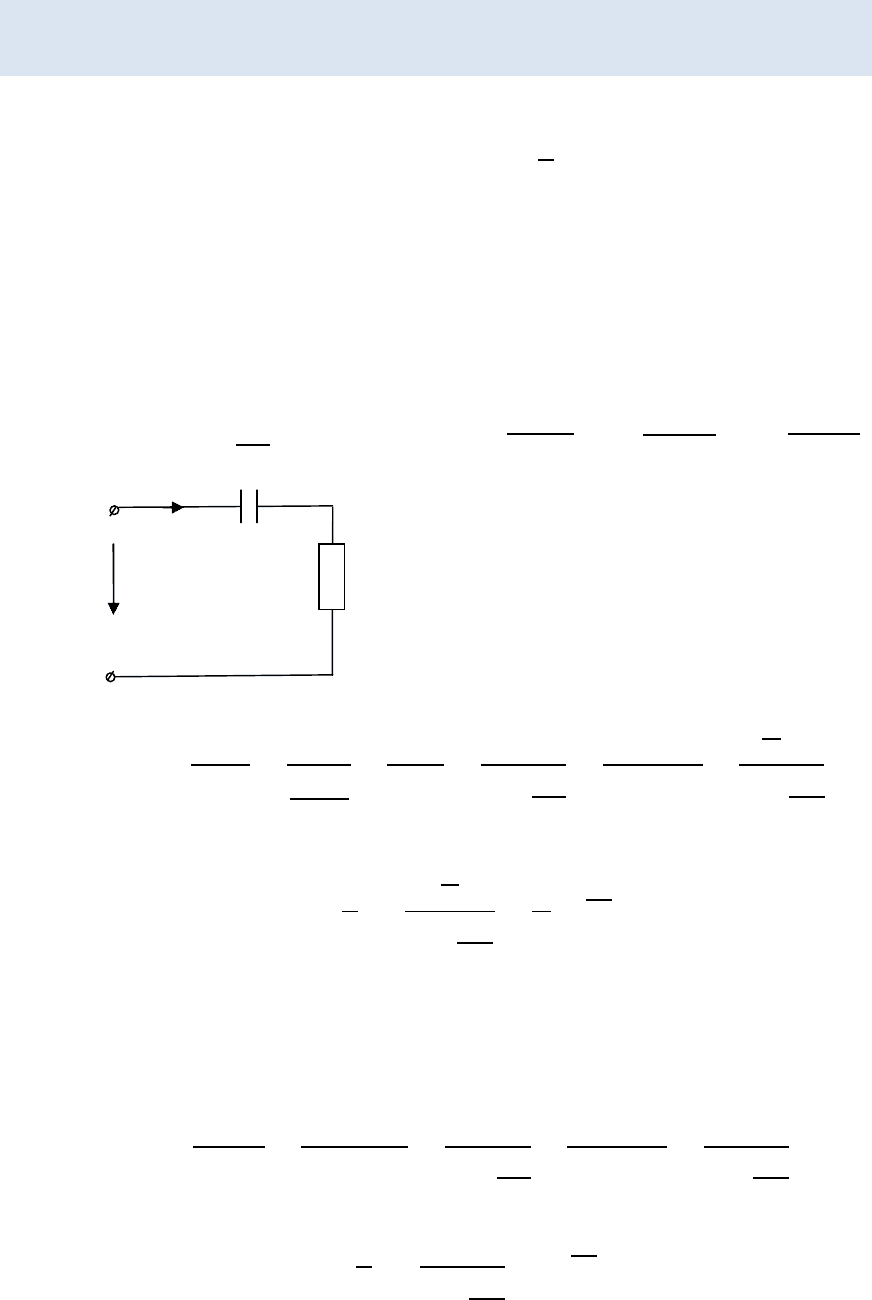
68
§3.4. СВЯЗЬ МЕЖДУ ОПЕРАТОРНОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИЕЙ
И ПЕРЕХОДНОЙ ХАРАКТЕРИСТИКОЙ ЦЕПИ
ℎ
(
)
=
(
)
⋅
1
(1)
— обратное преобразование Лапласа.
Покажем справедливость выражения (1) на том же примере.
1
)
(
)
ℎ
(
)
2
)
(
)
ℎ
(
)
3
)
(
)
ℎ
(
)
1)
(
)
=
(
)
(
)
=
1
(
)
(
)
=
1
(
)
=
1
+
1
=
+1
=
1
+
1
(
)
⋅
1
=
1
+
1
≓
1
2) Имеем
( ). Найти ℎ
( ).
(
)
=
(
)
(
)
=
(
)
(
)
(
)
=
+
1
=
+1
=
+
1
(
)
⋅
1
=
1
+
1
≓
R
U(p)
1
I(p)

69
3) По
( ) найти ℎ
(
)
.
(
)
=
(
)
(
)
=
(
)
1
(
)
(
)
=
1
+
1
=
1
+1
=
1
+
1
(
)
⋅
1
=
1
+
1
Воспользуемся теоремой разложения.
(
)
= +
1
=0
=0,
= −
1
(
)
=
+
1
=2 +
1
(
)
=
1
,
(
)
= −
1
(
)
=
1
1
+
1
−
1
=1−
§3.5. ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА ЦЕПИ
g(t)
a(t) — импульс воздействия.
(
)
=
(
)
(
)
|
н.н.у.
=
(
)
(
)
|
н.н.у.
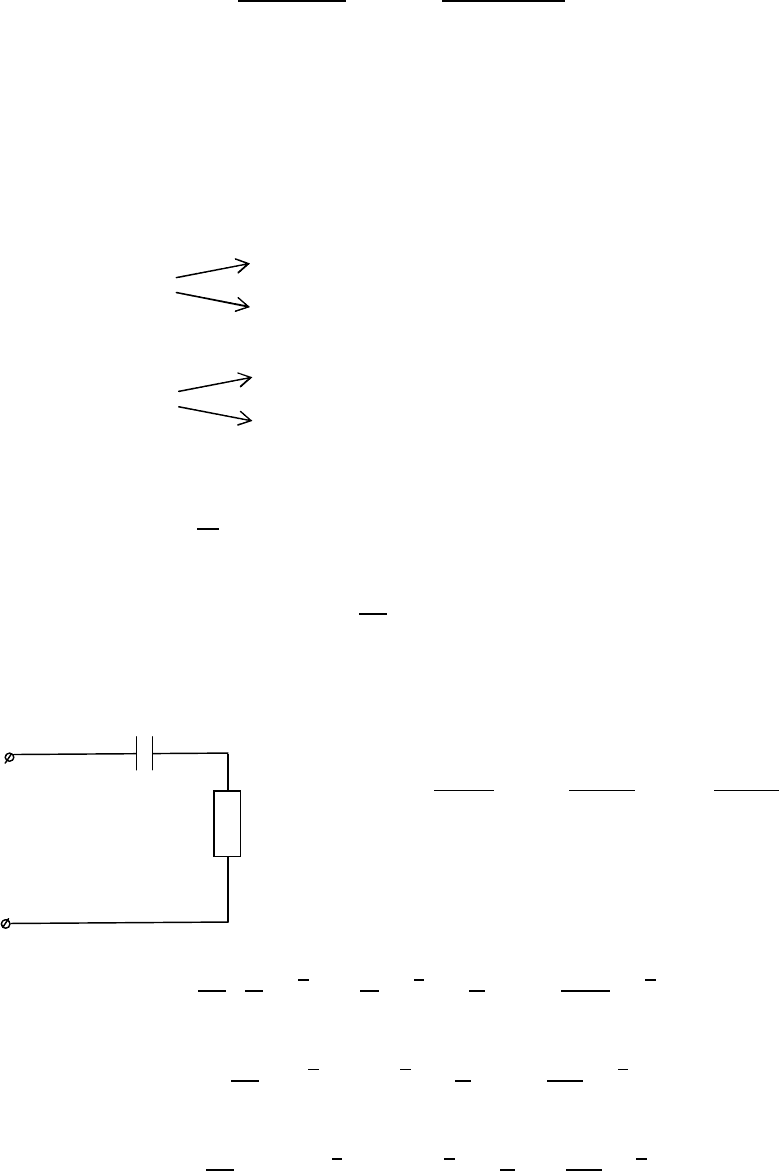
Импульсной характеристикой цепи называется отноше-
ние реакции цепи к импульсу воздействия при нулевых на-
чальных условиях.
ЭЦ
a(t) b(t)
70
Если импульсная функция с задержкой на время
, то
(
−
)
=
(
−
)
(
−
)
|
н.н.у.
=
(
−
)
(
−
)
|
н.н.у.
1) Импульсная характеристика — это фактически реакция це-
пи на функцию Дирака.
2) Размерности:
3) Поскольку
(
)
=
1( ), то
(
)
=
ℎ
(
)
.
Пример.
1
)
ℎ
(
)
(
)
2
)
ℎ
(
)
(
)
3
)
ℎ
(
)
(
)
1)
(
)
=
1
=
1
−
1
= −
1
2)
(
)
=
=
−
1
= −
1
3)
(
)
=
1 −
= −
−
1
=
1
R
u
i
u →
безразмерная
i → [Ом
-1
]
u → [Ом]
i → безразмерная
на входе
