Braibant S., Giacomelli G., Spurio M. Particles and Fundamental Interactions: An Introduction to Particle Physics
Подождите немного. Документ загружается.


464 A Appendix
For a free particle, one has P
2
D m
2
c
2
(we say that the particle is “on mass
shell”). The square of the total energy in the center of mass is called the s variable
and is written as
s D .p
1
C p
2
/
.p
1
C p
2
/
D .p
1
C p
2
/
2
D .P
1
C P
2
/
2
D E
2
cm
: (A.8)
Finally, the equations that describe the transformations of electric and magnetic field
components as a result of coordinate transformations (A.1)are
8
ˆ
<
ˆ
:
E
0
z
D E
z
E
0
y
D .E
y
C ˇB
x
/
E
0
x
D .E
x
ˇB
y
/
8
ˆ
<
ˆ
:
B
0
z
D B
z
B
0
y
D .B
y
ˇE
x
/
B
0
x
D .B
x
C ˇE
y
/:
(A.9)
They show that it is impossible to consider the electric field and the magnetic field
as independent entities.
A.3.2 The Formalism of Classical Electromagnetism
The classical theory of electromagnetism defines the fields E and B that obey the
Maxwell equations. They allow us to calculate E; B once we know the charge
density and the current density j. In the Gauss system of units (c.g.s.), the
Maxwell’s equations are
8
ˆ
ˆ
ˆ
ˆ
<
ˆ
ˆ
ˆ
ˆ
:
rE D 4
rB D 0
r E D
1
c
@B
@t
r B D
4
c
j C
1
c
@E
@t
(A.10)
where D dq=dv, j D v D Œdq=.dt dS/ On are respectively the charge density and
current density and On is the unit vector normal point by point to the surface S.Ina
vacuum, D D 1 and it is not necessary to define the vectors D e H.Thevolume
element can be written in one of the following notations: d v D d
3
x D d
3
r.The
force acting on a charge q moving with velocity v is
F D q
E C
v
c
B
: (A.11)
One can say that there are Coulomb forces between stationary electric charges
and additional forces (magnetic) between moving charges. Accelerated electric
charges emit electromagnetic radiation, which can then be diffused or absorbed by
bodies containing electric charges.
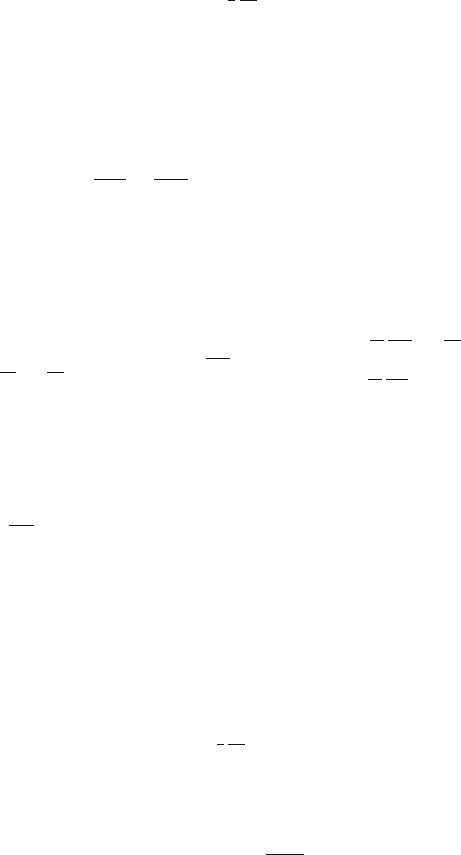
A.3 Basic Concepts of Relativity and Classical Electromagnetism 465
The fields E; B can be expressed in terms of a scalar potential ' and a potential
vector A
(
E Dr'
1
c
@A
@t
B D r A :
(A.12a)
In relativistic notation, we consider the contravariant four-vector position x
D
.ct; x/, energy-momentum p
D .E=c; p/, current density J
D .c; j/, potential
A
D .'; A/ and the antisymmetric tensor
F
D
@A
@x
@A
@x
D @
A
@
A
: (A.12b)
The (A.12b) expressed in tensor form the equations relating the fields and potentials
described by (A.12a). In the vacuum, in covariant form, Maxwell’s equations are
not homogeneous, that is,
8
<
:
rE D 4
r B DC
@E
@t
C
4
c
j
9
=
;
A
D
4
c
J
8
<
:
5
2
A C
1
c
2
@
2
A
@t
2
D
4
c
j
5
2
' C
1
c
2
@
2
'
@t
2
D 4
(A.13)
and are written in tensor form through a single equation, that is,
@
F
D
4
c
J
;F
D
0
B
B
B
B
@
0 E
x
E
y
E
z
E
x
0 B
z
B
y
E
y
B
z
0 B
x
E
z
B
y
B
x
0
1
C
C
C
C
A
(A.14a)
where J
. D 0; 1; 2; 3/ are the four components of the four-vector charge density
and current density .
For the two homogeneous equations
rB D 0
r E D
1
c
@B
@t
;
the tensor form is
F
Œ;
D 0; or
3
X
;;D0
@F
@x
D 0 (A.14b)
where F
Œ;
D @
F
and the parenthesis indicates the sum over all cyclic
permutations with sign, F
Œ;
D @
F
C@
F
C@
F
.
is the completely
antisymmetric Ricci tensor with
0123
D 1.
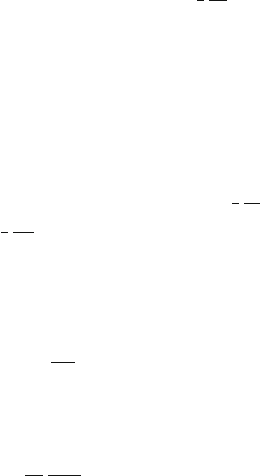
466 A Appendix
The expression of the covariant electromagnetic tensor is obtained by F
D
F
, with
matrix of the metric , namely,
D
0
B
B
@
10 0 0
0 10 0
0010
00 01
1
C
C
A
: (A.15)
F
is obtained from F
by changing E !E and B ! B, i.e., the electric field
is described by a polar vector and the magnetic by an axial one.
A.3.3 Gauge Invariance of the Electromagnetism
One important property of the electromagnetic field is the gauge invariance.The
observable fields E and B are invariant if ' and A change in the following way:
A
! A
0
D A
@
(
' ! '
0
D '
1
c
@
@t
A ! A
0
D A C r:
(A.16)
These transformations are called gauge transformations. The scalar function can
be a constant (then one has a global gauge invariance) or a function that varies from
point to point (local gauge invariance).
From the relation B D r A, it is evident that the vector potential is defined,
leaving its divergence as a free parameter. The choice rA D 0 identifies the class
of the so-called Coulomb gauge. The choice adopted here, rA C
1
c
@
@t
D 0, is called
the Lorentz gauge. One has rA
0
C
1
c
@
0
@t
D 0 if we request that the scalar function
satisfies D 0.
The electromagnetic field can be described by the four-vector potential A
.x
/
that obeys (A.13), which can be written in the form
A
.x
/ D
4
c
J
.x
/:
In vacuum, without sources, one has
A
D 0 )
1
c
2
@
2
A
@t
2
r
2
A D 0;
and the solution is
A
D e
e
iqx
)
!
A D
O
e A
0
expŒi.K r !t/

A.4 Dirac Equation and Formalism 467
where A
0
represents the amplitude, ! D 2 is the pulsation, K is the wave-vector
which represents the direction of wave propagation,and
O
e represents the polarization
vector which indicates the direction along which the field E oscillates.
A.4 Dirac Equation and Formalism
A.4.1 Derivation of the Dirac Equation
The Klein–Gordon equation (4.12) contains second derivatives with respect to time
and space coordinates; it is adequate for particles of integer spin (such as the photon,
in the limit m D 0) . Dirac proposed an equation that would satisfy the energy-
momentum relativistic relation (E
2
D p
2
C m
2
), but containing only first order
space-time derivative. It is considered to be an equation of the type E D i„
@
@t
D
H . The simplest linear operator for the Hamiltonian H is (here, we always use
the units c D 1)
H D ˛p Cˇm (A.17)
where ˛ D .˛
1
;˛
2
;˛
3
/ is a vector quantity and ˇ a scalar one; they are defined so
that H
2
D p
2
C m
2
. This is verified if
˛
2
i
D 1 I ˇ
2
D 1I .˛
i
˛
j
C ˛
j
˛
i
/ D 0I .˛
i
ˇ C ˇ˛
i
/ D 0: (A.18)
Since the quantities ˛
i
and ˇ anticommute between them, they cannot be simple
numbers, but must be matrices of size at least 4 4. As a consequence, the function
is a column vector with four components (spinor). The explicit form of ˛ and ˇ
is not unique and we follow the representation of Dirac–Pauli:
˛ D
0
0
I ˇ D
1 0
0 1;
(A.19)
where are the 2 2 Pauli matrices:
1
D
x
D
01
10
;
2
D
y
D
0 i
i0
;
3
D
z
D
10
0 1
(A.20)
and 1 is the 2 2 identity matrix.
The Dirac equation can be as well represented with the matrices ˛
i
and ˇ, with
the matrices
defined as
D ˇ˛I
i
D ˇ˛
i
.i D 1; 2; 3/I
0
D ˇ: (A.21)
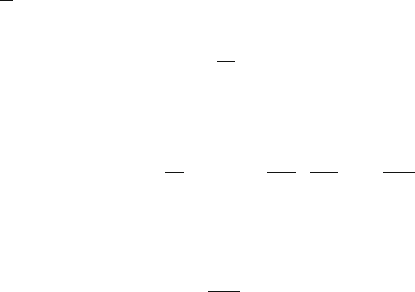
468 A Appendix
In this way, it is easy to show (Problem 4.9) that the eigenvalue equation E D
i„
@
@t
D H can be written as
i„
0
@
@t
C i„r m D 0: (A.22)
If we use the four-vector notation,
@
@t
; r
@
@x
o
;
@
@x
i
@
@x
@
; (A.23)
the (A.22) can be written in a compact form as
i
X
@
@x
m D 0I D 0; :::; 3: (A.24a)
If the sign of summation over is implied, the most compact form is
.i
@
m/ D 0: (A.24b)
From (A.21), it follows that .
0
/
2
D 1; .
i
/
2
D1;
D
and the
matrices can be expressed as
k
D
0
k
k
0
with k D 1; 2; 3I
0
D
0
D
1 0
0 1
I
5
D
0 1
1 0
(A.25a)
or explicitly, as
0
D
0
B
B
@
10 0 0
01 0 0
0010
00 0 1
1
C
C
A
;
1
D
0
B
B
@
0001
0010
0 100
1000
1
C
C
A
;
2
D
0
B
B
@
000i
00Ci0
0 Ci0 0
i0 0 0
1
C
C
A
;
3
D
0
B
B
@
0010
0001
100 0
0100
1
C
C
A
: (A.25b)
In addition, the
5
matrix is defined as
5
D
5
D i
0
1
2
3
D
0
B
B
@
0010
0001
1000
0100
1
C
C
A
with
2
5
D 1I
5
C
5
D 0: (A.25c)

A.4 Dirac Equation and Formalism 469
A.4.2 General Properties of the Dirac Equation
Before discussing solutions, some important properties of the Dirac equation are
shown.
Invariance property. The Dirac Hamiltonian H (A.17) commutes with the angu-
lar momentum operator J: ŒH; J D 0 (Problem 4.10), where
J D„l C
1
2
„ : (A.26)
H also commutes with the pseudoscalar generalized helicity operator :
D
p
p
0
0
p
p
!
(A.27)
so that ŒH; D 0 (see Problem 4.11). The helicity operator also commutes with the
momentum Œ; p D 0. The Dirac Hamiltonian can inherently describe the motion
of particles with half-integer spin with spin oriented along the direction of motion,
as discussed in detail in Sect. A.4.4.
Adjoint equation. Let us separate the (A.24) in the space-like and time-like part:
i
0
@
@t
C i
k
@
@x
k
m D 0 (A.28)
with k D 1; 2; 3. We define the adjoint spinor as:
0
D
T
0
: (A.29)
It can be verified that the Hermitian conjugate of (A.28) can be written as
i
@
@t
0
C i
@
@x
k
k
C m D 0 (A.30)
whichisdefinedastheadjoint Dirac equation. By multiplying (A.28) to the left by
and (A.28) to the right by and summing, one obtains
@
@t
.
0
/ C
@
@x
k
.
k
/
@
@x
.
/ D 0; (A.31)
representing the continuity equation similar to that adopted in the case of the
Schr
¨
odinger equation in Chap. 4 (4.10)ifwedefine
J
.
/: (A.32)

470 A Appendix
The adjoint function has the remarkable property of allowing for the construction of
relativistically invariant quantities, for example, (A.32).
The Lagrangian density for a Dirac field. The Lagrangian L of a system is a
function that summarizes the dynamics of the system. If the Lagrangian is known,
then the equations of motion can be derived. The time integral of the Lagrangian is
called action, and is denoted by S.
In field theory, the Lagrangian density L is defined as the quantity which must be
integrated over all space-time to get the action S D
R
Ld
4
x. The Lagrangian is then
the spatial integral of the Lagrangian density. The Dirac equation is the equation of
motion for a suitable Lagrangian density obtained from variational calculus (see
Problem 11.1). The Lorentz-invariant Lagrangian density with (A.24b) as solution
is simply
.i
@
m/ D 0: (A.33)
The modern point of view is to start with a Lagrangian (or the action) as the
fundamental quantity from which field equations are derived (as we did in Chap. 11
for the Lagrangian density of the electroweak theory).
Relativistically invariant quantities. A Lorentz transformation between two in-
ertial reference systems along the x axis with relative velocity ˇ D v=c can be
expressed in the following form:
x
0
D
X
a
.ˇ/x
I a
D
0
B
B
@
.1 ˇ
2
/
1=2
ˇ.1 ˇ
2
/
1=2
00
ˇ.1 ˇ
2
/
1=2
.1 ˇ
2
/
1=2
00
0010
0001
1
C
C
A
: (A.34)
There is Lorentz-invariance of the Dirac equation if there exists a function
0
.x
0
/
which satisfies equation A.24 in the new coordinates x
0
:
i
X
@
@x
0
0
m
0
D 0I D 0; :::; 3: (A.35)
It can be shown that this function exists and can be represented as
0
D S I with S
1
S D
X
a
: (A.36)
S is an operator that only acts on the spinor of .
By combining the matrices with the wave function and its adjoint, five
objects mutually independent and relativistically invariant can be built. These are
shown in table Sect. 8.16.1, in column “currents.” See Problem 8.15.
Reversal of space coordinates and parity P. We have seen in Sect. 6.4 that the
operation of inversion of space coordinates is generated by the operator P called

A.4 Dirac Equation and Formalism 471
parity. Let us apply the reversal of space coordinates r !r to the Dirac
equation A.28:
i
0
@
@t
i
k
@
@x
k
m
.r;t/ D 0: (A.37)
.r;t/ is a wave function with the space coordinates reversed, and is not a
solution of the Dirac equation (note the sign of the discrepancy between the space
and time components of (A.28)and(A.37)). One should therefore seek a wave
function with the space coordinates reversed that is: (1) the solution of the Dirac
equation, and (2) Lorentz-invariant. To this purpose, let us multiply the (A.37)to
the left with
0
and use the property
0
k
D
k
0
:
i
0
@
@t
C i
k
@
@x
k
m
0
.r;t/ D 0: (A.38)
By comparison of (A.28)and(A.38), we have
0
.r;t/ .r;t/I
0
.r;t/ .r;t/: (A.39)
This equation shows that the operator
0
represents the parity operator (which
reversesthe space coordinates)for the wave function solutions of the Dirac equation.
Time reversal operator T. Similar to the parity operator, it can be shown that
under reversal of time coordinate (Sect. 6.7), the equation .r; t/ does not satisfy
the Dirac equation, while
3
1
.r; t/ D .r;t/I
1
3
K .r;t/ D .r; t/ (A.40)
does. K is the operator of complex conjugation: K
. As a consequence,
1
3
K (A.41)
represents the operator which reverses the time for the wave function solutions of
the Dirac equation.
Charge conjugation and parity operator CP. Less straightforward, is the proof
(see, for example, [Be08]) that the operator
i
2
K (A.42)
represents the operator which transforms the spinor .r;t/ into the spinor with
opposite energy, momentum and spin, that is,
.i
2
K/
C
D
.p/: (A.43)

472 A Appendix
Recalling the definition of charge conjugation and parity operator CP (Sect. 6.8), if
.r;t/ represents the particle state, i
2
K is the corresponding antiparticle state.
Then, the operator turns, for example, the neutrino state (D spinor with positive
energy) with negative helicity, into an antineutrino state (D spinor with negative
energy) with positive helicity, see Fig. 6.3.
A.4.3 Properties of the Dirac Equation Solutions
The Dirac equation is a set of four equations, each of which must have a solution.
These solutions are normally written in the following form:
D ue
i.prEt/
D ue
ip
x
(A.44)
where the space-time dependence e
i.prEt/
e
ip
x
is separated from that
depending on the spin u. The four component spinors u are constants and correspond
to 4 1 matrices. There is a very useful representation, namely,
D
e
i.prEt/
(A.45)
where and are two component spinors. As an exercise (Problem 4.12), we
demonstrate that inserting (A.45) in the Dirac equation results in
D
p
E m
(A.46a)
D
p
E Cm
; (A.46b)
forming a homogeneous system which admits solution only if E
2
p
2
m
2
D 0.
We obtain again a quadratic relation, similar to that already obtained with the Klein–
Gordon equation whose solutions are
E D˙
p
p
2
C m
2
; (A.47)
including solutions with negative energy. Dirac suggested that all states with
negative energy are fully occupied. The creation of a e
C
e
pair is explained as
the transition (induced by a photon with energy E
>2m
e
c
2
)ofanelectronina
negative energy state into a positive energy state. The lack of an electron (a hole)in
this sea of particles with negative energy represents a positron.
An additional difficulty arises from the consideration that if all the negative
energy states are filled, the energy of the vacuum state is 1. Dirac solved this
issue, assuming that measurable quantities correspond to a variation with respect to
the vacuum state, in analogy with the classical potential energy. As the measured

A.4 Dirac Equation and Formalism 473
values are deviations from the vacuum state, the Dirac theory cannot predict mass
and electric charge of particles. This aspect (renormalization) is common to all field
theories.
The homogeneous system (A.46) has two dependent variables (; ) which are
crossed in the equations and give rise to four solutions (taking into account the sign
of energy). The 2 C 2 solutions are
for E DjEjW D
p
jEjm
I D
p
jEjCm
I (A.48a)
for E DjEjW D
p
jEjCm
I D
p
m jEj
: (A.48b)
The choice of the independent spinor ( or ) is guided by physics considerations.
Nonrelativistic limit. Let consider the nonrelativistic limit where p ! 0 and E !
m C p
2
=2m. Then,
p
jEjm
!
p
p
2
=2m
!1;
p
jEjCm
! 0: (A.49)
In this case, the (A.48) become
for E>0W ! 0Ijjjj (A.50a)
for E<0W ! 0Ijjjj: (A.50b)
Since two solutions vanish, we consider the two remaining as arbitrary functions.
To represent them, as the Dirac equation describes spin 1/2 particles, for ; ,we
choose the eigenstates of the operator
3
(the projection of the third component of
the spin operator), that is,
3
D˙I
3
D˙: (A.51)
It is straightforward to verify that the eigenstates can be written as
R
D
1
0
I
L
D
0
1
R
D
1
0
I
L
D
0
1
(A.52)
where the indices L and R will be clarified in the following. With this choice, the
four solutions of the Dirac equation are
for E DjEjW
C
N u
C
e
i.prEt/
D N
p
jEjCm
e
i.prjEjt/
(A.53a)
