Brewster H.D. Fluid Mechanics
Подождите немного. Документ загружается.

72
Basics
of
Fluid Kinematics
Projection in
~:
die X - X - Ebene
e
1 -2 ,
V Projection in
..
die X
1
-
X
2
-
Ebene
~.
t----~-
Bahnlinie
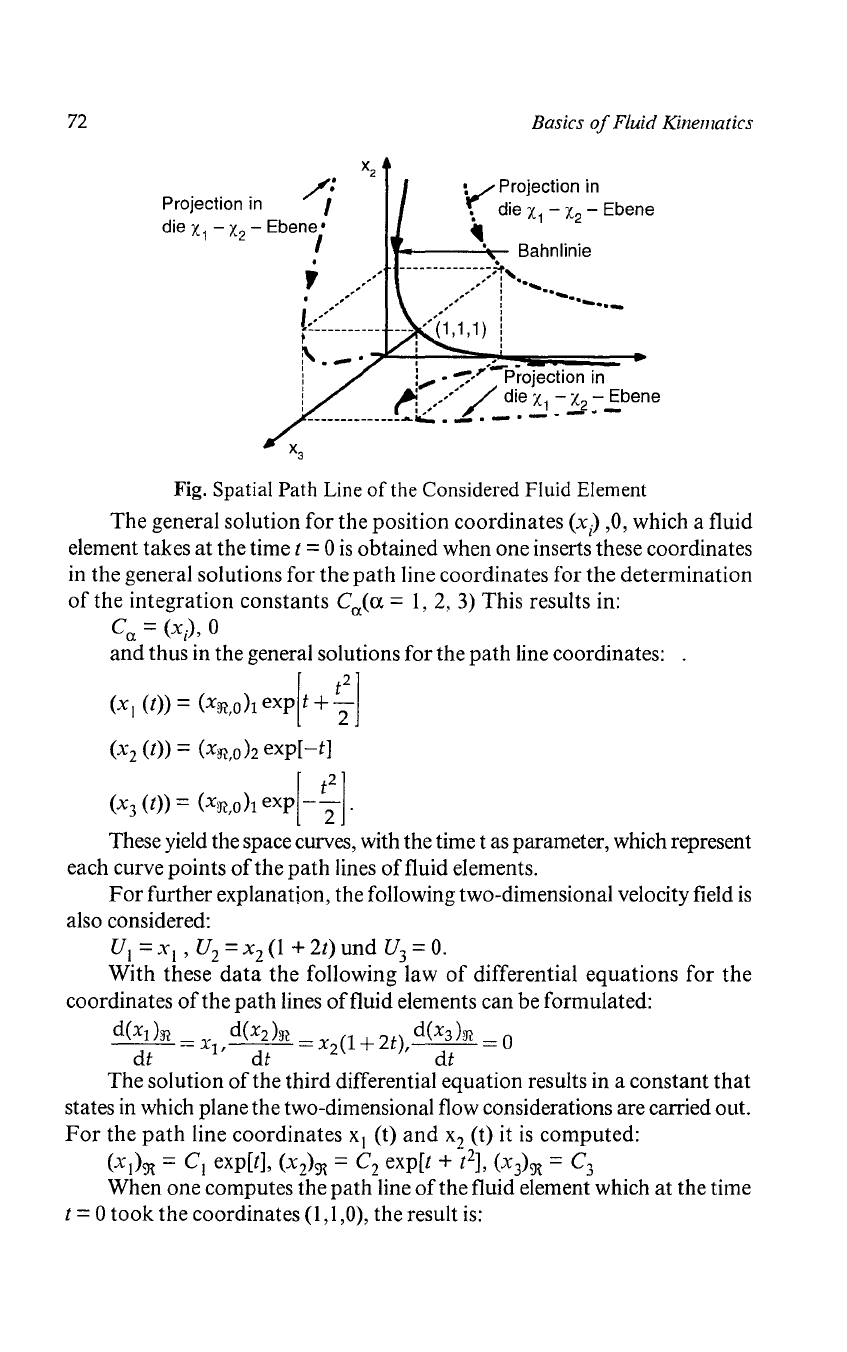
Fig. Spatial Path Line
of
the Considered Fluid Element
The general solution for the position coordinates
(x)
,0, which a fluid
element takes
at
the time t = °
is
obtained when one inserts these coordinates
in the general solutions for the
path
line coordinates for
the
determination
of
the integration constants Ca(a =
1,2,
3)
This results in:
C
a
=
(x),
°
and
thus in the general solutions for the
path
line coordinates:
(XI
(t»
=
(x3?,oh
exp[t + t;]
(x2
(t»
=
(x3?,oh
exp[-t]
(x3
(t»
=
(x3?,oh
ex
p
[-
t;].
These yield the space curves, with the time t as parameter, which represent
each curve points
of
the
path
lines
of
fluid elements.
For
further explanation, the following two-dimensional velocity field
is
also considered:
VI = x I ' V
2
= x
2
(l
+ 2t)
und
V3
=
0.
With these
data
the
following law
of
differential equations for
the
coordinates
of
the
path
lines
of
fluid elements can be formulated:
d(xlh~
,d(x2)3? _
(1
2)
d(x3h~
- 0
dt
Xl'
dt
- X2 +
t,
dt
-
The solution
of
the third differential equation results in a constant
that
states in which plane the two-dimensional flow considerations are carried out.
For
the
path
line coordinates
xI
(t)
and
x
2
(t) it
is
computed:
(x
I
)9t
= C
I
exp[t],
(x
2
)9t
= C
2
exp[t + t
2
],
(x
3
)9t
= C
3
When one computes the
path
line
of
the fluid element which at the time
t = °
took
the coordinates
(l,
1,0), the result
is:
Basics
of
Fluid Kinematics
73
(X
I
)9t
= exp[t],
(x2h
= exp[t +
1],
(x
3
)9t
= 0
When
one
resolves
the
equation
obtained
for
(xI) with respect to
time, it yields:
t=
In(x
I
)9t
When inserted in the solution for
(x
2
)9t
for two-dimensional
path
lines in
the plane
x
1-
x
2
- the following functional relation between
(x
Ih
and
(x2)9t
yields:
(x)
= (
)(1+ln(x
Jl
:Rl
• 2
9t
XI:R
Sweeping Paths of Locally Injected Tracer Materials
It
is
usual in experimental fluid mechanics to gain qualitative insight in a
flow process
by
injecting a continuous fluid tracer
at
a fixed position. This
leads to a marked
"fluid thread" which
is
carried with the flow
and
thus marks/
traces the course
of
the flow.
When the exact course
of
the flow
is
of
interest, quantitative evaluations
of
the
location coordinates
of
sweeping
paths
of
locally installed tracer
materials are required. These evaluations can,
based
on
the
derivations
stated
below,
be
carried
out
with methods
of
flow kinematics.
Attention
is
drawn
to
the fact that this flow field
is
not
source-free, thus
it violates
the
requirements/demands
of
the
continuity equation. This is,
however, insignificant for the purely kinematic considerations mentioned here.
2.0
-r--r-------r---,
1.0 -
0.0
-+------......---+---..-----1
.
0.0
1.0
x,
2.0
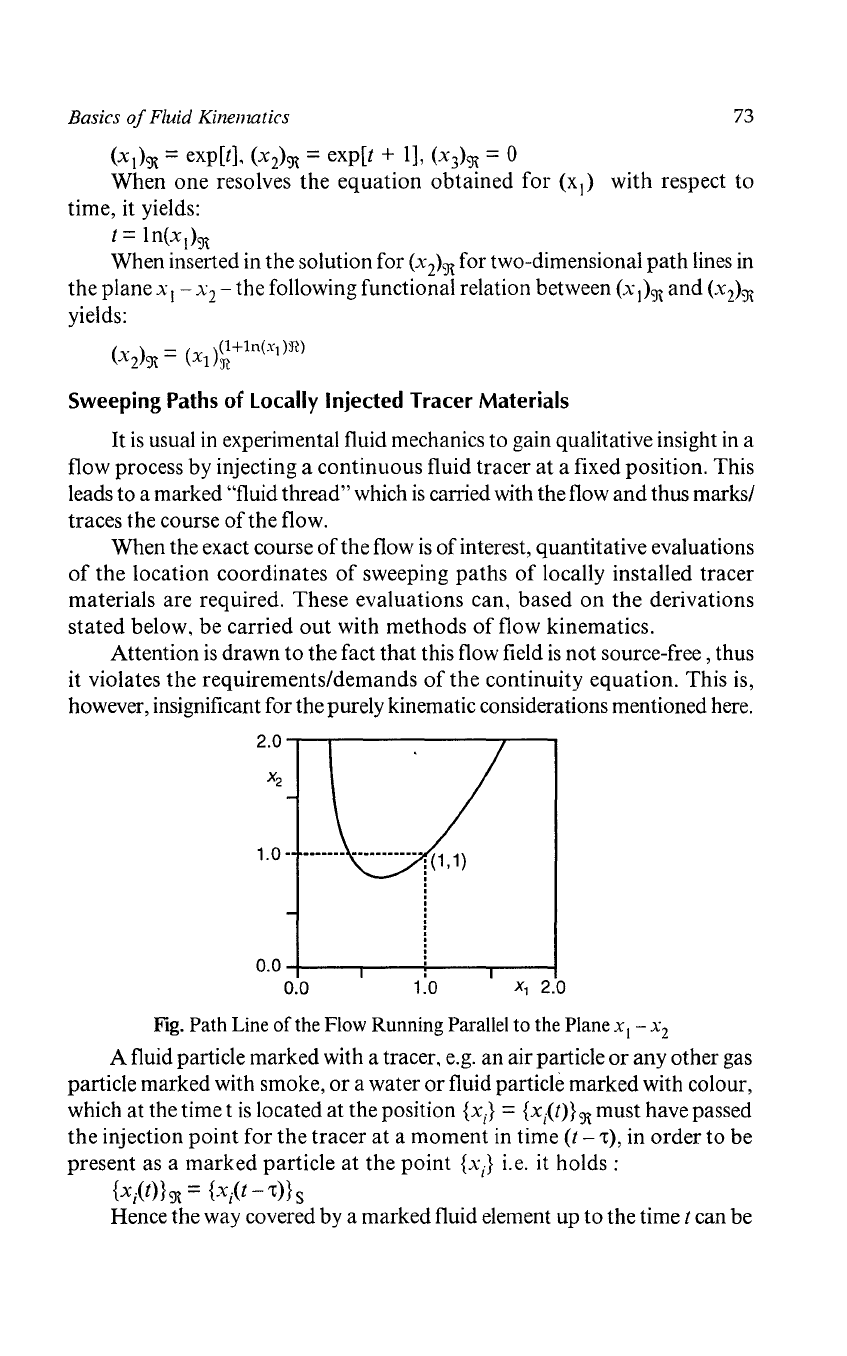
Fig. Path Line
of
the Flow Running Parallel to the Plane x I - x
2
A fluid particle marked with a tracer, e.g. an air particle
or
any other gas
particle marked with smoke,
or
a water
or
fluid particle marked with colour,
which at the time t
is
located at the position
{xJ
=
{x
i
(t)}9t must have passed
the
injection
point
for
the
tracer
at
a
moment
in time (t - 't), in
order
to be
present as a
marked
particle at the
point
{xJ
i.e. it
holds:
{x
i
(t)}9t =
{xi(t-'t)}s
Hence the way covered by a marked fluid element up to the time t can be

74
Basics
of
Fluid Kinematics
computed as path line
of
the element that fulfills the condition i.e. a path line
with the initial condition that for
f =
1:
the fluid element held the position
of
the location coordinates
of
the injection point. The sweeping path thus
is
composed
of
the sum
of
the path lines
of
individual particles. For each
individual marked particle
of
a sweeping path a parameter
1:
is introduced,
which for
0
~
1:
~
f covers all parts
of
a sweeping path.
It
is
therefore important
to vary the parameter
1:
in
the solution equations
in
order obtain the entire
sweeping path.
The above short explanations shall be made clear again by way
of
an
example, which
is
handled on the basis
of
the three-dimensional velocity field
used above:
U
I
=
Xl
(1
+ f), U
2
=
-x
2
and U
3
=
-x3f
This velocity field yields the law
of
differential equations for the motion
of
a fluid element in
space:
d(Xl)S
=X
(l+t)
d(x2)s
=X
d(x3)S
=-x
t.
dt
1
'dt
1
'dt
3
As a solution one obtains for the components(xl)s '
(x
2
)s
and (x
3
)s
according to equation:
lThe index s signifies that the location coordinate
of
the sweeping path
is meant.
(xl)s = C
1
exp[t(l
+±)j,
(x
2
)s
= C
2
exp
[-
f], (x
3
)s
= C
3
ex
p
[-
t;].
When one inserts now the initial conditions, that
(xl)s
= (xl)t=t =
1,
(x
2
)s = (x
2
)t=t =
1,
(x
3
)s=
(x
3
)t=t = 1
was present for t
=
1:,
i.e. that the position (1,
1,
J) serves as an injection
point
of
the tracer, one obtains:
C
l
=
exp[-T(l+~)j;
C
2
=
exp
[1:]
and C
3
=
exp
[T:].
Inserted in the solutions for (xI)s, (x
2
)s
and (x
3
)S
the equation
of
the
frequency locus defined as sweeping path yields for all times:
(xl)s =
exp[t(l+±)-T(l+~)j,
(xl)s = exp
[-(t
-
1:)],
(xl)s = ex
p
[li(t
2
_T2)j
When one wants to make visible the course
of
a sweeping path at a moment
in time
f (partly), one has to insert the value
oft
in the above equation in order

Basics
of
Fluid Kinematics
75
to obtain in this way the equation
of
a space curve, with
't
as a parameter.
Here
t is determined by the period
of
time
['t
l
'
't
2
]
of
the tracer injection in
(1,
1,
1)
with
-00
<
't
l
<
't
2
<
t.
For
't
l
~
-
00,
't
2
= t and t = 0 yields:
(xI)s
= eXP[-T(l
+~)l,
(x
2
)s
= exp
['t],
-
00
<
't
< 0
(x
3
)s
= ex
p
[
T:
J
The course
of
this space curve
is
shown in 4.4.
It
indicates the sweeping
path existing at the moment in time
't
= 0 (made visible from
't
= -
00
to
't
= 0,
the projections
of
the sweeping path into the main level
of
the Cartesian
coordinate system are also introduced.
Wh~n
one compares the equation for the sweeping path fixed by the space
point (1,
I,
1)
with the equations for the path line
of
a fluid element, stated for
the same flow field, one realizes that path lines and sweeping paths are not
identical for non-stationary flows.
Only
in
the case
of
a stationary flow field
path lines and sweeping paths are identical, as can be shown easily by the
following considerations.
As a space curve is concerned here, the statement
in
x
I'
x
2
'
x3
- coordinates
is appropriate. The definition
Xs
indicates that the location coordinates
of
a
sweeping path are meant.
X
2
Injection x
2
-
x3
Projection
x - x
ProJ'ection
of the sweeping path
2 3
~
of the sweep\in
g
pa:h//
-:;;/1"
..
r---
(1.1.1~
_.'
j1
I
"/"
, I I /
----
/ Sweeping path
,/
./
,/
X
2
-
x3
Projection
of
the sweeping path
Fig. Sweeping Path for the Moment in Time t =
O.
with Fluid Tracer
Injections Between
t = -
00
and t = 0 at the Position (1,
1,
1)
Considering the stationary velocity field:
U
I
= 2x1 ' U
2
=
-x
2
,
U
3
=
-x3
one obtains for the path line
of
a fluid element the following differential
equation:
d(xI
h~
2
d(X2
»)R
_
d(X3
»)R
_
dt
XII
dt
-
-X21
dt
- X3

76
Basics
of
Fluid Kinematics
for t = 0 it shall be assumed
that
(xI):R
= (x
2
):R
= (x
3
):R
= 1 so that in the
solution
(xl)
= C
I
exp [2t], (x
2
):R
= C
2
exp
[-
t], (x
3
) = C
3
exp [-t]
holds and thus the path line is stated as follows:
(xI):R
= exp [2t],
(x2
):R
= exp
[-t],
(x
3
):R
= exp
[-t]
with
-00
< t <
00.
For the computation
of
the sweeping paths the solution
can
be employed again and C
I
,C
2
,
C
3
can be computed such that it is claimed
that
at
the time t = 't holds:
(xl(t
=
't»s
= I, (x
2
(t =
't»s
= 1, (x
3
(t
=
't»s
= 1
Therefore it holds:
C
I
= exp [-2't], C
2
= exp ['t], C
3
:::;
exp ['t]
or
as an equation for
the
sweeping path:
(xl)s
=
exp[2(t
- 't)], (x
2
)s = exp
[-(t
- 't)], (x
3
)s = exp
[-(t
- 't)]
thus t being defined, and the range
of
values
of
t is defined
by
the period
of
time
of
the tracer injection. In the case that tracer substance is injected
at
all times, i.e.
-00
<
't
<
00,
equation yield the same curve.
When
the tracer
injection
is
limited
in
time,
one
obtains
as
a
visible
sweeping
path
a
corresponding
part
of
the path line.
U
I
=
xl'
U
2
=
xiI
+ 2t) and U
3
= 0
which leads to the differential equations:
d(Xl):R
_
d(x2h~
_
(1
2t)
d(x3h~
0
~~"'--
x:R'
-
Xw
+ ,-'---'=<..:..:""-
dt dt dt
with
the
solutions:
(xI):R
= C
I
exp [t], (x
2
):R
= C
2
exp [t(t + 1)], (x
3
):R
= C
3
On
the other hand, when one demands
that
the particle located
at
the
time t in
the
point x
I'
x
2
'
x3
passes
the
injection point (1,
1,
0)
of
a tracer
at
the
moment in time
't the integration constants CI' C
2
and
C
3
can
be obtained
from the following conditional equations:
C
1
exp ['t] =
1,
C
2
exp
['t('t +
1)]
=
1,
C
3
= 0
2,0...,.------------,
~
1,0 - ------------------:-,
I :
i l
,
0,0
•
0,0
1,0
Xl
2,0
Fig. Sweeping Path in the Plane x I - x
2
(Fully Drawn Line
Corresponds to
--00
S;
't
S;
0, Broken Line to 0
S;
't
S;
00)
These "constants" can now be inserted in equation again, where C
3
= 0

Basics
of
Fluid Kinematics
77
signifies that the sweeping path runs in the plane
xl
- X
2
' i.e. in the plane
x3
= 0, and is described there by the following equations for the position
coordinates (xl)s and
(x
2
)s
(xl)s = exp
[t
- 't],
(x
2
)s=exp
[t(t+
l)-'t('t+
1)]
For the moment in time
t = 0 the course
of
the sweeping path is:
(xl)s
= exp [-'t],
(x
2
)s
= exp [-'t('t + 1)]
in the domain
-
00
< 't <
00.
From the equation for
(xl)s
follows:
t =
-In(xl)s
Inserted in the equation for (x
2
)s
at
the time t = 0 the existing course
of
the sweeping path made visible by the injection
of
tracer material in
-00
< 't <
00
results in the plane
xl
- x
2
(x
2
)s
=
(Xl)~l-ln(Xl)s)
in the domain 0 < (x1)s <
00
(x
2
)s
=
[(x1)s]<1-ln(Xt)s)
KINEMATIC QUANTITIES
OF
FLOW
FIELDS
Flow
Lines
of a Velocity
Field
The considerations carried out in for fluid elements for the com-putation
of
path
lines
and
sweepings
paths
have
to
be
separated strictly
from
considerations for the determination
of
the flow lines
of
a flow field. Although
for stationary flows flow lines, path lines and sweeping paths are identical,
this does not
justify
to neglect the fundamental differences or even worse to
assume that they do not exist.
Only by a clear separation
of
the con-siderations
it becomes generally comprehensible why under the steady-state condition
of
a flow field the above-stated identities
of
flow lines, path lines and sweeping
paths exist.
When one considers the non-stationary
flqw field
f1
(xi' t), flow lines
can be defined for this field at any moment in time t so that space curves run
parallel
to
the velocity vector which are defined as flow lines
at
each point. In
the case that one considers initially a two-dimensional flow field, for which
all velocity vectors lie parallel to the plane xl
- x
2
'
then the above-indicated
definition
of
the flow line leads
to
the following defining equation:
d(X2)1j1
U
2
- for the time t = const
d(xl)1j1
U
I
The relation means that the gradient
of
the flow line
is
equal to the tangent
of
the angle formed by the velocity vector with the axis xl at the moment in

78
Basics
of
Fluid Kinematics
time
t.
The index 'l'taken up
in
the equation indicates that the stated coordinates
xl
- x
2
describe the flow line
'1'.
x
2
X3
= const
Velocity vector
Stream line
Fig. Sketch for Clarifying the Defining Equation for the Flow Line
of
a Flow Field
When one considers the defining equation for the flow line
of
a two
dimensional flow field, it becomes comprehensible that in general for each
moment
in
time t the quotient
of
V
2
and VI is a function
of
xl
and x
2
.
The thus
resulting differential equation has to be solved in order to conserve the equation
for the flow line.
This will be explained on the basis
of
an example that starts from the
following two-dimensional velocity field:
VI =
xl
(1
+ 2t); V
2
= x
2
and
V3
= 0
Introduced into the defining equation for the flow line one obtains:
d(x2)'I' V
2
x2
---'-
= - =
---==---
d(Xl)'I'
VI
xl(l+
2t)
or
d(x2)'I' = d(Xl)'I'
x2
Xl
2+
2t
By integration results:
1
In(x
2
)'I' = C + 1 +
2t
In(x
2
)'I'
Considering the flow line, passing at time t = 0
at
the point (1,
1,0)
C =
o results and thus:
1
(X
2
)'I'
= [(Xl)'I'
]1+21
In the case that there is a three-dimensional velocity field, the above con-
siderations, that were indicated for the projections
of
the flow lines into the
planes
xl
- X
2
.,
can be accepted in an analogous way. For the projections into

Basics
of
Fluid Kinematics
79
the planes xl -
X3
- and x
2
-
x
3
•
relations analogous to the defining equation
result:
d(x3)", U
3
--"'-=-
d(XI)",
U
I
d(x3)", U
3
--'-=-
d(x2)", U
2
Thus the defining equations
of
the flow lines
of
a velocity field can be
stated as follows:
d(XI)",
_ d(x2)",
d(XI)",
= d(x3)", d(x2)", = d(x3)",
U
I
U
2
U
I
U
3
U
2
U
3
or rewritten as:
d(XI)",
= d(x2)", = d(x3)",
U
I
U
2
U
3
These differential relations for the flow line
of
a velocity field hold at
each moment in time
t.
Their solution leads to a relation
(x
3
)'I'
=
'I'(xl'
x
2
),
which describes a space curve, the three-dimensional flow line.
Probably the most simple way to solve the law
of
differential equations
is
to seek a parameter soluti9n (xl)", =
Xl
(s), here s
is
a parameter, whose
value at a certain reference point
of
the flow line
is
equal
to
zero and which
takes increasing values along the flow line and in flow direction. When all
values
-00
< S <
00
are passed, through a presentation
of
the entire flow line
is
obtained.
By introducing s one obtains:
d(x.)
~
'"
=
~
(xi' t) for t = const and j = s
a relation which represents for each coordinate (x)", a differential equation
j =
1,
2, 3 describing the flow lines in space for t = const.
If
the flow line
passing through the space point
[xo]j at time t is sought, s =
0,
results from
integrating the three differential equations, when
x/t)
=
Xj,O
From this results
the entire flow-line field as:
(x)", = 'l'j
(xo,j
,
t,
s)
In order to demonstrate the way
of
proceeding in determining
three-dimensional flow-line fields, the following velocity field is to be
considered again:
U
I
= x
l
(1
+ t), U
2
=
-x
2
and U
3
=
-x3t
Thus a law/principle/theorem
of
differential equations for the flow lines
of
this velocity field results:

80
Basics
of
Fluid Kinematics
d(XI)1jI
d(x2)1jI
d(X3)1jI
ds = x
l
(1
+ t) ds = -X2
ds
= -x3
t
The integration
of
these equations yields:
(xI)1jI
= C
I
exp
[(1
+ t)s],
(x
2
)1jI
= C
2
exp [-s],
(x
3
)1jI
= C
3
exp [-ts].
Searching for the flow line that passes through the
point(l,
1,
1)
one can
chose this point as a point
of
reference and set s = 0 for (xi)", = 1 From this the
following results for the integration constants:
C
I
= C
2
= C
3
= 1
One obtains thus:
(xI)1jI
= exp
[(1
+ t)s],
(x
2
)1jI
= exp [-s],
(x
3
)",
= exp [-ts].
For the time t = 0 a flow line path results
(xl)", = exp [s], (x
2
)",
= exp
[-s],
(x
3
)",
= 1
• So one obtains a flow line passing in the plane
x3
= 1 and described there
by the relation
1
(x
2
)",
=
-(
)
Xl
IjI
The entire flow line field is obtained when one introduces for s = 0
arbitrary position coordinates (xo) so that for the position coordinates holds:
(xI)1jI
=
(xI)IjI,O
exp
[(1
+ t)s]:
(x
2
)1jI
= (x
2
)IjI,O
exp [-s],
(x
3
)1jI
= (x
3
)IjI,O
exp [-ts].
This set
of
equations indicates at each time t the flow lines passing through
the point
{X·},1I0
There the parameter s has the value s =
o.
and for all other
}
T'
points
of
the flow line a value equal to zero. A clear assignment is thus
occurring which guarantees that flow lines never intersect, as otherwise two
velocities would exist simultaneously at this point
of
intersection. Thus
occurring which guarantees that flow lines never intersect, as otherwise two
velocities would exist simultaneously at this point
of
intersection. This is
excluded because
of
the existence
of
clear velocity fields (except for stagnation
points and singularities).
.,
In the preceding section it was emphasized that in general flow lines,
path lines and sweeping lines are not identical and the computed examples
have made this clear have confirmed this. For stationary flows all three lines
are identical, i.e.
Basics
of
Fluid Kinematics
81
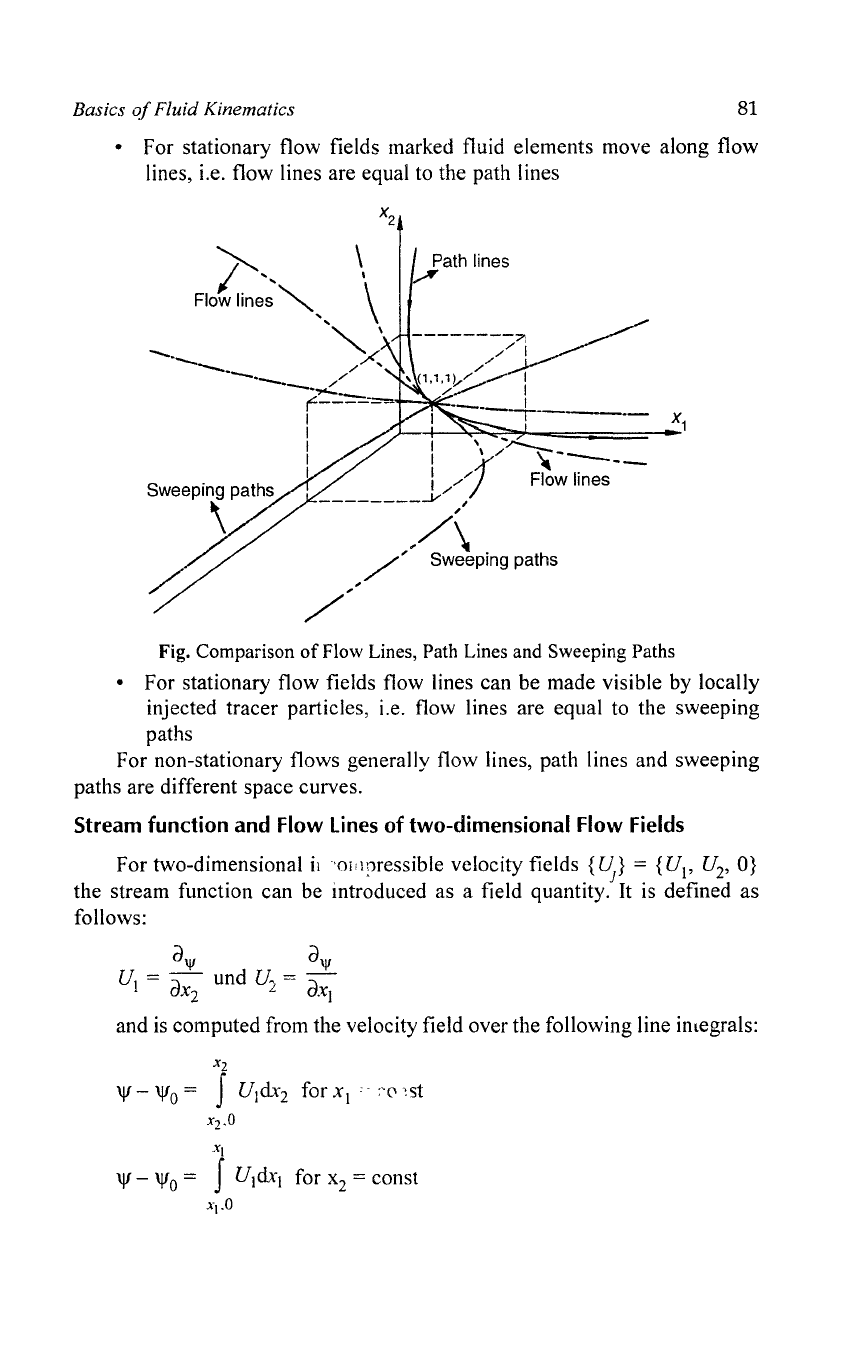
• For stationary flow fields marked fluid elements move along flow
lines, i.e. flow lines are equal to the path lines
,~~,~~:~
/~
I
___
I
I
--r-----
X
1
I
,~
I \ /
\---_
I
//1
Flow lines
________
.Y
,
,/\
,/'
Sweeping paths
/'
Fig. Comparison
of
Flow Lines, Path Lines and Sweeping Paths
• For stationary flow fields flow lines can be made visible by locally
injected tracer particles, i.e. flow lines are equal to the sweeping
paths
For non-stationary flows generally flow lines, path lines and sweeping
paths are different space curves.
Stream function and Flow
Lines
of
two-dimensional Flow Fields
For two-dimensional il'olil:1fessible velocity fields
{V}
=
{VI'
V
2
,
O}
the stream function can be introduced as a field quantity.}
It
is defined as
follows:
and is computed from the velocity field over the following line inlegrals:
Xl
'"
-
"'0
= f V
1
dx
2
for x
1-
:'('
:st
x2·
0
x,
'"
- "'0 = f Vldx
l
for x
2
= const
x,.o
