Будішевський В.О. Проектування транспортних систем енергоємних виробництв

Подождите немного. Документ загружается.

чина резерву всієї транспортної лінії приймається за мінімаль-

ним значенням з отриманих.

Технологічний резерв продуктивності конвеєрної лінії

обумовлений нерівномірністю вантажопотоку, що надходить на

конвеєр, і величина його коефіцієнта розраховується за форму-

лою

)(1

−= ,

де Q

– експлуатаційне навантаження, т/година.

Технічний резерв продуктивності цієї лінії залежить від

можливостей засобів транспорту в заданих умовах експлуатації і

установлюється за формулою

−= ,

де Q

– технічно можлива продуктивність, т/хв.

Величина резерву продуктивності конвеєра визначається

сукупністю технологічного і технічного резервів, а величина ко-

ефіцієнта резерву продуктивності – залежністю

)1)(1(1

)(1

−−−=−= .

За умов завантаження конвеєра з усереднюючої ємності

величина технологічного резерву продуктивності дорівнює ну-

лю (r

=0). При цьому величина резерву продуктивності визнача-

ється тільки технічними можливостями конвеєрів

−== ,

де Q

– продуктивність розвантаження бункера, т/година.

У випадку завантаження конвеєра рівномірним вантажопо-

током з ємності і нерівномірним з одного очисного вибою вели-

чини коефіцієнтів резерву продуктивності визначаються за фор-

мулами:

161

еб

−=

Σ)(1

еб

−= .

Величина загального резерву продуктивності в цьому ви-

падку встановлюється за формулою

−=

)(1

За умов завантаження конвеєра декількома вантажопото-

ками, розподіленими за довжиною конвеєра, визначається вели-

чина інтенсивності середньозваженого середнього хвилинного

вантажопотоку за формулами

aaa

nnnn

)(12)(11)(1

)(1

...

= , т/хв.

У цьому випадку коефіцієнти резервів продуктивності:

cе

)(1

⋅

−= ;

се

−= ;

)(1

1−= .

Коефіцієнти показують наявність наступних резервів: тех-

нологічних, технічних і продуктивності кожної конвеєрної уста-

новки.

Знак «-» кожного з видів резерву свідчить про наявність

«вузького» місця в даній точці транспортної системи.

Резерв продуктивності конвеєра в абсолютних величинах

(т/хв.) визначається за формулами:

162

R =

;

QrR

;

QrR

Резерв часу роботи конвеєрної лінії обумовлений відмова-

ми (кінцевою надійністю) власне транспортних установок і ха-

рактером надходження вантажопотоків з очисних вибоїв (наяв-

ність проміжків безперервного надходження і відсутність ван-

тажопотоку).

Величина коефіцієнта резерву часу транспортної лінії

встановлюється за формулою

= 1 – К

ов.

· ПК

г i

де К

ов.

– коефіцієнт надходження вантажу з очисного вибою;

ПК

гi

– добуток коефіцієнтів готовності конвеєра транспорт-

ного маршруту вибою.

Коефіцієнт готовності - основний комплексний показник

надійності:

/(T

де Т

– наробіток на відмову, що характеризує безвідмовність,

годин;

– середній час відновлення, що характеризує ремонтопри-

датність машини в розглянутий період часу, годин.

Нормативні мінімальні значення коефіцієнта готовності і

термінів служби конвеєрів різних типів, обумовлені відповідни-

ми стандартами, наведені в таблиці 5.1. Практично, в окремих

випадках конвеєри можуть працювати при коефіцієнті готовнос-

ті К

= 0,98...0…0,99

Таблиця 5.1.

Тип конвеєра К

Термін

служби,

рік

Ресурс до першого капіталь-

ного ремонту, тис. годин

Стрічковий: стаціонарний і

напівстаціонарний

0,96 8 8000 – 1000

163

Більші значення коефіцієнта готовності досягаються шля-

хом підвищення технічного рівня конструкції конвеєра або

збільшення трудовитрат на обслуговування і ремонт.

Значення кожного показника надійності повинне бути по-

годжене зі співвідношеннями паспортних і фактичних даних

машини – режимом її завантаження і умовами роботи. Очевид-

но, що за умов недовантаження і перевантаження машини, при

меншій або більшій швидкості руху стрічки показники надійно-

сті будуть різними. Цю дуже важливу обставину необхідно бра-

ти до уваги під час аналізу тих або інших абсолютних значень

показників, отриманих на основі обробки статистичних даних.

У схемах комплексної механізації транспортно-

технологічних ліній можливе послідовне (що має найбільше

поширення), паралельне і комбіноване розташування окремих

конвеєрів, що становлять загальну систему.

П1

П2

П3

П4

П1

П2

П3

П4

П1

П2

П3

П4

К1

К2

К3

К4

ПР1

ПР2

ПР3

ПР4

Н1

Н2 Н3

Н4

НС

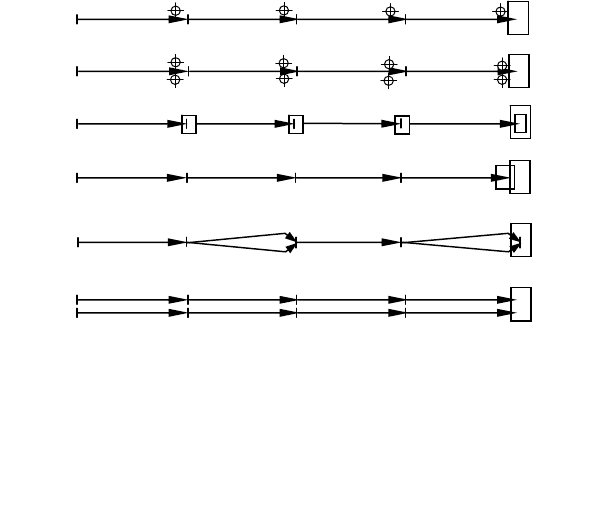
Рисунок 5.10. Схеми послідовного розташування окремих конве-

єрів К

, К

, ... К

у загальній системі:

а − без резервних пристроїв (П1, П2 − приводи конвеєрів 1, 2, ...);

− з резервними пристроями ПР1, ПР2 ...; в − з накопичувачами H у

кожного конвеєра; г − із загальним накопичувачем НС; д − з дублю-

ючими лініями Д у окремих конвеєрів; е − з дублюванням усієї сис-

теми конвеєрів

164

Послідовна система конвеєрів може не мати (рис. 5.10а,б)

або мати накопичувальні пристрої в кожному окремому конвеє-

рі (рис. 5.10в) або у всієї системи (рис. 5.10г), мати дублюючу

лінію для окремих складових частинах (рис. 5.10д) або усієї сис-

теми в цілому (рис. 5.10е). За умов відсутності накопичувальних

пристроїв зупинка будь-якого окремого послідовно

розташованого конвеєра викликає зупинку (відмова) усієї

системи. У цьому випадку імовірність безвідмовної роботи

системи Р

із i-го числа конвеєрів визначають як добуток

імовірностей Р

безвідмовної роботи кожного окремого конве-

єра:

∏

Загальний коефіцієнт готовності системи

∏

iгсг

де К

– коефіцієнт готовності кожного конвеєра системи.

Якщо в системі є накопичувачі, то безперервність потоку

вантажів зберігається у всьому робочому періоді при .

maxвін

tt ≥

При система зупиняється на час

maxвін

tt < ttt

нвісв

−

max.

(тут t

–

час дії (сумарний запас за часом) накопичувача, година; t

вimax

–

максимальний час ліквідації відмови на конвеєрах системи, го-

дина.

За умов наявності повної резервної (дублюючої) лінії час

зупинки системи складе лише проміжок часу, необхідний для

передачі сигналу і включення дублюючої лінії. Останню мають

стрічкові, пластинчасті, вібраційні і інші конвеєри в системах

особливого призначення, наприклад, у цехах паливоподачі елек-

тростанцій.

165

)

Під час визначення

імовірності б відмовної ро-ез

боти Р (t) складної системи

необхідно розчленувати її на

окремі елементи, для кож-

ного з яких окремо визна-

чають імовірність безв дмо-і

вної роботи. Для цього ши-

роко вик стовують струк-ори

турні схеми, у яких ко ний ж

елемент характеризується

своїм зн ченням мовірності а і

безвідмовно оботи протя-ї р

гом заданого періоду часу.

Найбільш характерний

випадок, коли відмова одно-

го елемента виводить із ладу

всю систему. Звичайно це

має місце за умов послідов-

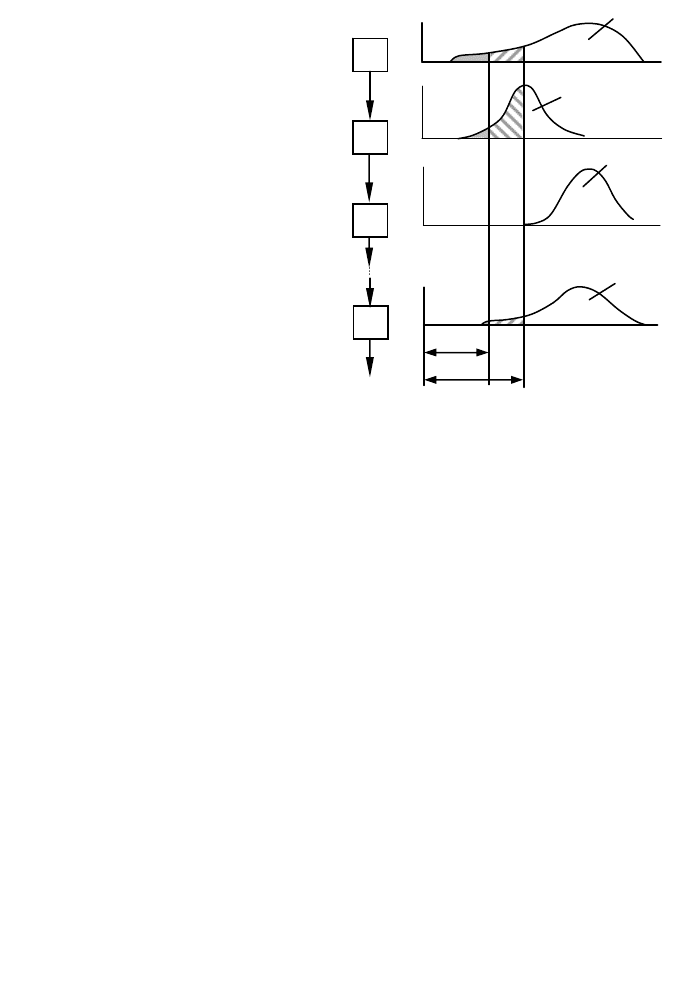
ного з'єднання елементів (рис.5.11а).

На рис. 5.11б показані криві розподілу термінів служби f(t)

для кожного елемента, які можуть бути отримані на основі ана-

лізу відмов роботи. Площа характеризує імовір-

ність відмови в заданому інтервалі часу, а імовірність безвідмо-

вної роботи буде дорівнювати Р(t) = 1 - F(t). З рисунка 5.11 вид-

но, що при збільшенні періоду Т

імовірність безвідмовної робо-

ти ряду елементів, а отже, і усієї системи зменшиться, тому що

вона дорівнює

∫

dttfF

)(

∏

tPtP

)()(

За умов однакових значень P

надійність системи буде до-

рівнювати

PtP =)(.

Рисунок 5.11. Послідовне з'єднання

елементів складної системи:

а − схема з'єднання; б − закони розпо-

ділу термінів служби елементів

(t)

)

(t)

(

)

(t)

166

З наведених формул виходить, що складна система, укла-

дена з великої кількості елементів, з'єднаних послідовно, буде

мати малу надійність. Так при числі елементів n = 10 з однако-

вою імовірністю, рівною 0,97, імовірність безвідмовної роботи

системи буде дорівнювати Р(t) = 0,97

=0,74.

Теорія ймовірностей дає ряд законів розподілу випадкових

величин, які використовуються для вирішення завдань надійно-

сті. Нормальний закон розподілу (Гаусса) у ряді випадків можна

застосовувати при зношуванні і інших поступових відмовах.

При асиметричних законах розподілу f(t) можуть бути викорис-

тані закони Вейбулла, Релея: логарифмічно нормальний, експо-

ненціальний або гамма-розподілу. Підставою для вибору закону

служать дані випробувань або відомості про аналоги.

Наприклад, якщо вихід з ладу елементів системи пов'яза-

ний з раптовими відмовами, що підкоряються експонентному

закону, то імовірність безвідмовної роботи таких елементів ви-

значають за формулами:

ePePePeP

λ−λ−

==== ;;;

321

де λ = 1/Т

ср

– інтенсивність відмов, які є зворотною величиною

середнього наробітку на відмову.

Імовірність безвідмовної роботи такої системи буде дорів-

нювати

∏

λ−

etP

)( .

Для підвищення надійності складних систем застосовують

дублювання навантажених елементів. У цьому випадку імовір-

ність спільної появи всіх відмов F(t) знаходять відповідно до те-

ореми множення

∏

FtF

)(

Наприклад, якщо імовірність безвідмовної роботи кожного

елемента системи P

= 0,90, а число паралельних елементів n=3,

то P(t) = 1 - (0,1)

= 0,999. Таким чином, імовірність безвідмов-

ної роботи такої системи значно підвищується.

167

Під час завантаження конвеєрів з ємності з інтенсивністю

коефіцієнт резерву часу визначається за формулою:

iгзо ..4

ПКKr 1

−

де

)(1

=ζ

– відношення величини середнього вантажопотоку,

що надходить у ємність, до продуктивності її

вивантаження.

В абсолютних величинах резерв часу транспортної лінії

протягом базового проміжку часу встановлюється за формулою:

гл

TKrR

, хв.,

де К

гл

– коефіцієнт готовності лінії;

Т - тривалість зміни, хв.

Коефіцієнт резерву пропускної здатності конвеєрної лінії

розраховується за формулою:

)1)(1(1

435

rrr −

−

а в абсолютних величинах (т/доба) - за формулою:

змmгл

nТQKrR

де n

зм

– число видобувних змін у добу.

Резерв технологічних ємностей дає можливість судити про

наявність потенційних можливостей транспорту для споруджен-

ня в його системі додаткових бункерів.

Величини коефіцієнтів резервів ємностей системи, що

акумулює і усереднює, визначаються за формулами:

∑

−=

max

1 та

∑

−=

max

де Е

а і

, Е

у і

– фактичні величини ємностей, що акумулюють і усе-

реднюють, установлених у системі транспорту;

а max і

, Е

у max і

– максимальні необхідні величини ємностей, що

акумулюють і усереднюють.

168

Перед установленням величини r

необхідно перевірити

відповідність установлених у конкретних місцях транспортної

системи величин ємностей, що акумулюють, і необхідних для

компенсації заданого обсягу простоїв. Для цього визначаються

величини Е

а max

точки транспортної системи, у якій фактично

перебуває ємність. При цьому обсяг компенсації простоїв Z по-

винен бути скоректований на величину добутку коефіцієнта го-

товності всіх конвеєрів до ємності, що розглядається:

∏

гi

KZZ

' ,

де i = 1, 2, ..., R – кількість конвеєрів у лінії, що передує ємності.

У подальших розрахунках приймається мінімальна вели-

чина ємності з отриманої розрахунком і фактично наявної в сис-

темі транспорту.

Величини Е

у max

визначаються для кожної транспортної лі-

нії, що транспортує вантажопотік зі своїм коефіцієнтом нерів-

номірності, за формулою

(

)

1)(1(max)1max

48,0 GaaE

⋅

−

⋅

де G

– середній час одного проміжку безперервного надхо-

дження вантажопотоку, приймається за хронометраж-

ним спостереженням, хв.

Величини наявних ємностей, що усереднюють, Е

перед

розрахунком резерву усереднюючої ємності також необхідно

зрівняти з максимальної необхідної, і в розрахунку величини

коефіцієнта резерву приймається найменше з отриманих зна-

чень. Одержання значень величин r

або r

зі знаком мінус озна-

чає відсутність резервів відповідних видів технологічних ємнос-

тей у системі і приймається r

=0 або r

=0.

Величини коефіцієнтів резервів ємності r

і r

рівні 1, ука-

зують на відсутність ємностей у розглянутих пунктах транспор-

тної системи, а величини R

і R

являють собою ті значення єм-

ностей бункерів, що акумулюють і усереднюють, які повинні

перебувати в цих пунктах. Негативні значення коефіцієнтів r

169

і величин R

і R

свідчать про надлишкову ємність у розгляну-

тій точці системи і показують її величину.

Величини резервів пропускної здатності системи розрахо-

вуються на основі величин резервів окремих конвеєрних ліній,

що входять у систему транспорту.

Величина кожного виду резерву для рівня ієрархії системи

визначається за формулою

∑

де – резерв пропускної здатності n-го рівня ієрархії системи;

R - кількість конвеєрних ліній в n-му рівні ієрархії системи;

R – резерв пропускної здатності i-ї транспортної лінії j-го

виду резерву.

Оцінка величини резервів пропускної здатності транспорт-

ної системи в цілому розраховується за формулою.

{

}

RR min= .

Наведений алгоритм установлення пропускної здатності

систем конвеєрного транспорту діючих шахт може бути викори-

станий для керування різних рівнів із застосуванням персональ-

них ЕОМ. Методи можуть бути застосовні і під час використан-

ня інших видів транспорту.

Приведені у відповідність пропускні здатності різних

транспортних ланок забезпечують ефективне транспортування

корисної копалини і створюють передумови для підвищення ви-

робничої потужності шахти.

170