Бугай П.Т. Теорія помилок і спосіб найменших квадратів

Подождите немного. Документ загружается.

або, розкривши дужки і підсумувавши по стовпчиках,

{[аа] Qtl+ [ab] Ql2+[ac] Q13-k.. + [at] Qlk}x і

+ {[ab] Q u 4- [bb] Q 12+ [be] Q 13 + ...+ [bt] Q i*} y і

+ {[ac] Qu + [6c] Q,о + [cc] Q13 + ...-f[c<] Qi*}z +

+ {[a^] Qu 4- [bt[ Q 124- [ct] Q 134 -...4 - [tt] Qi*} u-\-

4- [al] Qn -\- [bl] Qi2_b [cl] Q)34-...Л~[Щ Qi* = 0 .

Підберемо тепер неозначені множники Qn, Qi2, . .

гак, щоб вирази у фігурних дужках дорівнювали:

[аа] Qn 4- [ab] Qn 4- [ас] Q13 +... + [at] Qxh = 1,

[a&]Qn + [feb]Q12+ [bc\ Q13 + -\-[bt] Qlk = 0,

Iac] Qn + \bc]Qi2+ [cc] Q134-...4-[c*]Qi* = 0,

]at] Qn -i- [bt] Qx2 4- [rf] Q13 + . . . + [^J Qi* = 0.

Тоді рівняння (59,1) набере такого вигляду:

х + [al] Qu 4- [Ы] QVi+ [с/] Qi3 + ••• I \tl] Qik — 0.

Розкриємо в цьому рівнянні суми:

х + (aJi + a2l2 4 а313 т ... -г ап ln ) Qn +

+ (й(/( + b2l2 "I' Ь31в +... + b„l„) Qi2 +

- (^i^i 4“ с212 с^13 + . • • т сп ln ) Qjjj т

4-(^iIf + t2l2 4- t3l3-і-... і tnln)Q\tt — 0,

або. розкривши дужки і підсумувавши по стовпчиках.

х+ (^(Qn 4- btQv> 4 С j Q і з 4- 4- ^Qi*) lx 4-

+ ( a 2Q u f b2Q 12 4- c2Qи 4 -... 4-t2Q\k)l24-

4-(a^Qn + b3Ql2 + c3Qlsl-Y ... + ^3Qi«j)/3-t-

I (й/i Q, і 4" Q12 4" с/і Q]3 4" ••• ґ tnQ\k) In = 0.

Введемо для скорочення записів такі позначення:

<Zj = e1Q]i 4-ftiQi24-c1Q13 + ... 4-^iQi*,

(t2 — a2Q 114 b2Q 12 4- c2Q\3 4 -...4 - t2Q

a :j = a 3Q 1, 4 ^ 3Q i= + C8Q j34 ... 4 tzQ\h,

y*n *** a^ Qn 4" b,7 Qi2 4- Cn Qi3 4 + tn Qifc.

(59,1)

Qu-

(59,2)

(59,3)

3 «ими одержимо таку остаточну формулу, яка дає ви

раз для першого невідомого в функції величин Л, І2, , ІП

і неозначених множників Qu, що визначаються із системи

рівнянь (59,2):

X + Я1/( + а 2^2 "ї- а 3^3 + •••+ ®л In — 0,

або

Х = — ( а і^1 + а 2^2 а 3^3 "Ь . .. 4- / л ) . (59,5 )

В такий же спосіб визначається і решта невідомих у,

г, . . . , и ,в функції величин / і неозначених множників Q. Але

для кожного з цих невідомих вводиться своя система множни

ків, а саме:

Q iit Q ‘12< Q 23> ••• 1 Q i k Д Л Я У,

Q 3J. <3з;> Q 33. Q 3* * г, (59,6)

Q /г 1, Q ft2 , Q ft3 , Qfefe n « ,

які визначаються з таких систем рівнянь відповідно:

I аа] Q2i + [a&] Q2 2 -r[ac] Q23 + ... -і- [a£] Q > - 0 ,

[ab] Q21+[W>1 Q32 + [6c] Q23 + ... + [W] І,

[ac] Qo,+[frc] Q 22 + [cc] Q2s г fc/1] Q 2fr = 0, (59,7)

\at]Q2l r|W |Q 22 ! \ct] Q.,~ I-... + 1^1 Qa»-■(),

[aa] Q31+ [a&]Q32 + \ac] Q33-l-... -i-\at\ Q: ik П.

[ab] Q3l -і- I&&] Q3,-h |bc] Q33 +... -r [W] Q3ft = 0,

lac] Q31 + l*cj Q3, + [cc] Q33 + ... + H ] Q3* = l, (59,8)

\at] Q3I + [M] Q32+ H J Q:t:. ... \ti) Qi* = 0 ,

[aaj Q* i-t [ab] Q* 2 + [ac] Qft3 + ... + [a*] Qfcfe = 0,

[ай] Qfti + [M]Qft2 + [be] Qk3 + ... і- [W]Q*ft -0 ,

M Q fei + [H Qk2 + [cc] QH +...+ M Q t t =0. (59,9)

[atfj QkiJr[bt] Qk*+[ct] + Qkk = 1.

Рівняння, які входять до складу систем (59,2), (59,7).

(59,8) і (59,9), називаються ваговими рівняннями.

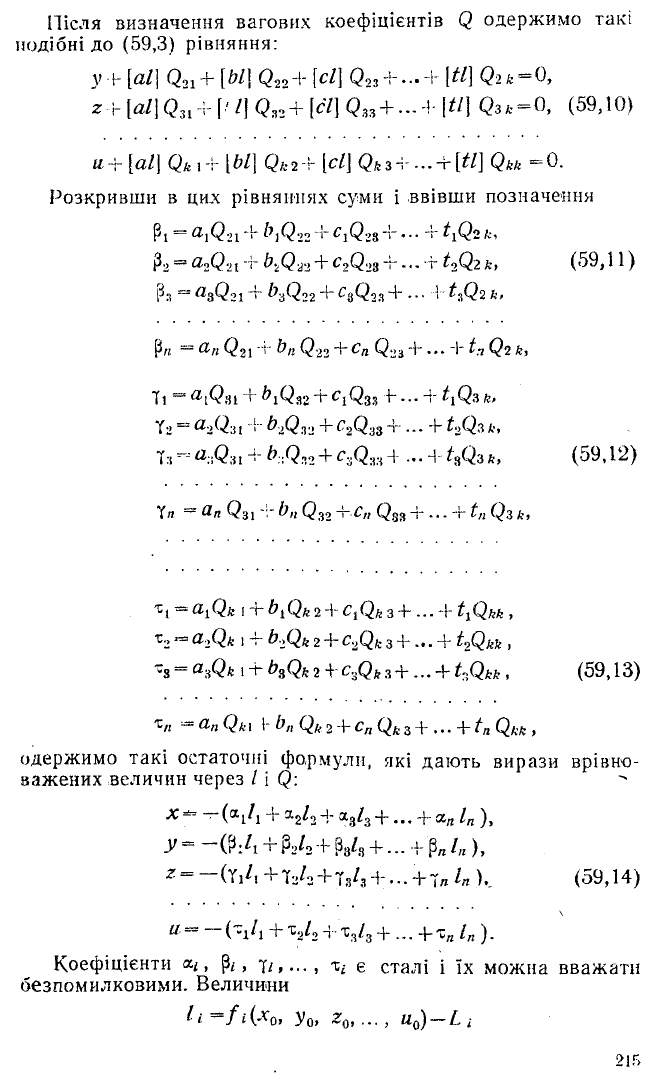
Після визначення вагових коефіцієнтів Q одержимо такі

подібні до (59,3) рівняння:

у + [al\ Q2i+ [bl\ Q2o+ \cl] Qo3 + ... і- [tl\ Qik^O,

z i-[a/]Q3 1 4[.'/|Q,2 +[c/]Qas + ...4-(«] Q s k - O , (59,10)

u+[al\ Qkl+ [bl\ Qk2-r [cl\ Qk3+... + [«] Qkk = 0 .

Розкривши в цих рівняннях суми і ввівши позначення

pi — ^ j Q22 * 1Q28 _1_ •' * ^1^2 к->

= a,nQ2l -r Ь.&^ + c2Q.,s-r ... т t2Q2к, (59,11)

1^:1 “ ®sQ?l 4 bsQ22 "1“ ^SiQ23 + • ! ^xQ^ к>

prt —

й п

Q 2I '*

Q22 ’"

€n

Q 23

" ••• I"

^:l

Q 2

Ti ~ a iQsi + ^iQs2 + сіРзз + ■•■ + ^iQsk,

Ї2- «2Q31 ! b2QK+c2Q33 +... + tzQzit,

b,QM + c3Qs:i-\- ... + t3Q3k, (59,12)

Yn — Q-n Q31 г b n Q32 +-C„ QS3 + ... -r t n Q3 *,

'ti =«iQ* і + ^iQ/г2 + CjQft 3+ ... + txQkk ,

v.,^a.,Qk і -r b.yQk 2 -f- 3~f*... + t2Qkk,

"s = anQk 1 + bsQk 2 ■} c3Qft3+ ... + t~Qkk, (59,13)

xn ^anQki t- b„ Qh 2 + cn Qfc 3 4-... + tn Qkk,

одержимо такі остаточні формули, які дають вирази врівно

важених величин через / і Q:

Х ~ ~ ( a Jl + а2^2 + а3^3 + ••• + ял Іп ),

У ~ (Р:Л -г Ь>2^2 "Ь SWs + ••• + Рл hi),

г - - ( їі Л + 7 3/3+ тЛ + - + Т піп).. (59,14)

a— +х2/2 -j-т3/3 + ... /„ ).

аі > рі > Ті.-.-, є сталі і їх

[. Величини

~fi(x0. Уо> ~о> ••• > м0) — L і

Коефіцієнти аг, р/, Ті .---, є сталі і їх можна вважати

безпомилковими. Величини

мають ту. саму., середню квадратичну помилку т, що й ве

личини Lt. Беручи де до уваги, знаходимо середні квадра

тичні помилки тх, ту, ... ,ти, застосовуючи при цьому фор

мулу (18,14):

т х2 = а^ т2 + а22 т2 +...+ ап 2т2 - т2 [ааJf

ту'г = $^ т? + ... + $„2т2 = т2 [р^],

OTjr2 = Y12OTa + Ta2m2-f ...+'(п2т2--=т2 [yyL (59,15)

т и2 = V пг2 + х2г пі2 + ... + х„ 2/я2 = т.2 [хх].

Припишемо результатам безпосередніх рівноточних вимі

рів ваги, рівні одиниці. Тоді за відомою формулою (29,3)

знайдемо ваги рх , ру , рг > , ри врівноважених невідомих:

тг 1

Р х '~"~тк 8 — [аа] ’

-171і 1

„ '«* (59,16)

...

|л] ,

/п2 1

Щоб виразити ваги рх, ру, Рг, •••, Ри безпосередньо че

рез вагові коефіцієнти Qrs (r, s= l, 2, 3,...,/<:), помножимо

послідовно кожне з рівнянь (59,4) спочатку на відповідні

(її, потім на Ьі, Сі, ..., a-і і, підсумовуючи кожен раз до

бутки по стовпчиках, будемо мати:

fact J - [аа] Q, t і- [ab] Qn + [ас] Q1S +... + [at] Qlk.

fba] = [ab] Qn V[bb] Qj3 + [ftcj'Qjg -I- ...r\-[bt] Q, k,

[ca\~[ac] Qu i [^ ]Q 12-l-[cc] Q:;, ( ... : |r/| Qlfc, (59,17)

[fa] = [a*]Qn l-[^]Qi2 + Qj8-f... + [tt] Qik,

[aa] = [aa] Qu + [ba] Q12 t- [ca] Q13 f ... + [£x] Qik.

Порівнюючи їх з ваговими рівняннями (59,2), знаходимо,

що

[aa] = 1, [fta] = 0, [£а]=0, ..., [fo] = 0.

Підставивши ці значення сум в останнє рівняння системи

(59,17), одержимо:

Помножимо далі кожне з рівнянь (59,1 ІУпослідОвно на

відновідні а-и потім bt, си ..., (З*. Підсумовуючи кожен раз

добутки по стовпчиках, будемо мати таку^рівняння:

[ар] = [аа] Qn + [ab]Q22 + [ac] Q23-bt.. + [atf] Q2*,

[Щ] - lab] Qai + [Щ Qm + ibc] Q z i/- + [Щ Qs ь,

[cp] = [ас] Q21 + [be] Q22 + [cc] + ... + [c^] Q2 k, (59,19)

[^P]= \аЦ Q.2і + [^] Q22 + [^TQ23 + ••• + [tt] Q2kr

[pp] = [ap] Q21 + [&P] Q22 + /p ] Q23 + ... + [^P] Q2£.

Порівнюючи їх з earoBHjfH рівняннями (59,7), знахо

димо:

[ар] = 0, Щ ]/\, [с|3] = 0, ..., [Щ = 0,

а також

[РР]— Qa2-

В такий же спосіб ми зможемо знайти, що

М У & , [*ї] = 0, [стг] = 1,

і, «арешті,

[flfl-o, [К) = 0 , [сх] = 0,

[тт] - Qes.

[<тг]-о,

[*х] = 1

[хх] = Qft*

(59.20)

(59.21)

(59.22)

(59.23)

Підставивши одержані значення величин [аа], [|3р], [y^],

•••* [хх] У вирази (59,16), остаточно будемо мати:

_ 1 _ 1 _ 1 _ 1

Рх ~ Он ’ Ру ~ Оі2 ’ Рг ~ О». ’ "',ри Qkki.

(59,24)

Другий спосіб. Щоб визначити ваги врівноважених неві

домих х, у, z, . .., и, можна скористатися загальною форму

лою (56,14), за якою визначається вага функції врівнова

жених аргументів:

н -р~ =

—M i f-zQz

/s?s •••

ҐкЧ к .

1 F

У цьому випадку вагові коефіцієнти Q будуть частковими

значеннями перехідних коефіцієнтів q, що відповідають част

ковим видам функції F(x, у, ?, .. ., и), вагу якої треба

знайти.

Справді, нехай заданна функція виглядає так:

F {х, у, z, и)-~х. (59,25)

Для визначення оберненої величини ваги цієї функції або,

що все одно, невідомого х, візьмемо часткові похідні по кож

ному аргументу:

/і= Ь Л -0 , / в- 0, f k 0. (59,2f.)

Неозначені множники q для заданого часткового виду

функції (59,25) позначимо так:

Яі ~ Qh> Qi2> Ч'і ' Q.3, ••■> (/>< Qia- (59,27)

Тут перший індекс при Q означає номер невідомого, дру

гий — номер неозначеного множника.

Підставимо тепер значення величнії / (59,20) і перехідних

коефіцієнтів (59,27) у рівняння системи (56,10), з розв’язімгия

якої знаходимо неозначені множники q:

[aa](-Qn) l-[aft](--Q12) + fac](-Q I3) | ... і [at\( Q,,,) І 1 0,

[ab](—Qi0 + [йй](— Q12) -і-[йс]( — Qi3) • t-... I \M]{~Qik) I <> 0,

fac](-Qn) + [M (—Qia)+ [cc]( —Qi3)-l ... -I |t71( Qi*) I 0 - 0 ,

И К - Qu) : [W](-Qia)+ H ( - Q n ) + - I- \tt\{ Q,*) ! 0 -0 ,

або, змінивши знаки,

[aa]Qn + [aft]Q124 [ac]Ql3+... I [a^Qi*— 1 -0 ,

[flft]Qu + [&£]Q12 + [ftc]Q13 +... + + 0 = 0,

[ac]QH + [&c]Q12+ [cc]Q,3+ ... - l - H ] Q u + 0 = 0 , (59,2 Я ) '

[fltf]Qn + [&£]Q12 + [c£]Q13 + ... + \tt\Qia і 0 = 0.

Таким чином, ми одержали ту саму систему рівнять для

визначення вагових коефіцієнтів Qu, що І в першому способі

Розв’язуючи їх, знаходимо Qn, Q12, Q13, Qi* Після під

стамовки Qn в р і витания (56,14) будемо мати:

=Q llf або Px^-q- • (59,29)

Ух VII

Припустимо тепер, що функція

F(x, у, z, и)=*у. . (59,30)

Та:к само, як і в попередньому 'випадку, знаходимо част

кові похідні функції:

/ і “ 0, Л = 1, /з = 0, 0. (59,31)

І її рі'ХІдмі коефіцієнти і.иі цього часткового .виду фупк-’

ції позначимо так:

Чі ' і> Vj Q: i </л Q‘2n> f/*= Q2A- (59,32)

Вони визначаються з ілких рівнянь: і

[aa]Q2l -І- I |(/c'|Q.j;, + ... -і- [a^]Q2* + 0 0,

fa6]Q-jj-l |М |(Л-:Н |/^')Q,,r i-... + [W]Q2* —1 О,. \

[ac]Q,r l-|/v|a.. і -f... I-frf|Q?H 0 = 0, (59,33)

И I Q-л 4 |^^]Q-23 + ••• + [^JQaft + 0 0.

Підстйвинши іпачення (59,31) часткових похідних функ

ції і вагові коефіцієнти (59,32), що визначаються з рівнянь

(59,33), у формулу (56,14), одержимо:

/7У = ~ - . (59,34)

Припустимо далі послідовно, що функція, вагу якої необ

хідно знанти, набирає такого вигляду:

F (x, у, z, ..., u )= z,

....................................

(59Г-5)

F (x , у, z, ..., и) = к.

Н цих випадках відповідно будемо мати:

а) значення часткових похідних:

/ . « о , / , - 0 , / я- 1 ......../* = 0,

........................................................ (59,36)

/ , - 0, / , = 0, / , - 0, ..., fk = 1;

G) позначення перехідних коефіцієнтів:

Qі ” Qsi, Я 2 ~ Q'j'j' Уз ~ Qssj **■* Qk~ Q3&»

......................................................................................... (59,37)

^ і = — Q fti, q > ^~~ Q k2 , ? з = — Q *3,

...............

4 k — Qkk\

в) системи рівнянь для визначення вагових коефіцієнтів:

[aa]Q31 + [fl6]Q3:> + [gc]Q83 +... 4- \(it\Qzk + 0 = 0,

[aft]Q31 + [fr&]Qs2 + [bc]Q33 + ... +[W]Q» + 0 -0 ,

fac|Q8i + [6c]Q32 + fcc]Qss+-... 4 f^]Q3fe—1=0, (59,38)

[a^]Qsl + [&^]Qg3 -!•- + ••■ + [ft]Q3* + 0 —0;

[aa]Qk і + [ab]Qk2 + fa^']Q*3 + ...+- [at]Qkk 4-0 = 0,

[aft]Q*i + [&&]Qfc2+ [6c]Qfe3-f... + [&^]Qft* + 0 = 0 ,

[ac]Qki + [bc]Q k2+ [c c ] Q * 3 + ... + [c^]Q*ft + 0 = 0, (59,39)

[a£]Q*i+ [ft^]Q*2 + [c^jQ*3 + ... + \ tt\ Q**—1= 0 ;

г) формули для визначення ваг врівноважених невідомих:

Л ~ а Г '

...............

(59,40)

” ТГ-

< іґ hk

§ 60. ВИЗНАЧЕННЯ ВАГОВИХ КОЕФІЦІЄНТІВ

З попереднього викладу видно, що для визначення ваг

врівноважених величин необхідно знайти к? вагових коефі

цієнтів Qrs (г, s = l ,2

.........

k), для чого треба розв’язати k сис

тем рівнянь (59,28), (59,33), (59,38), (59,39). Але легко по

мітити, що ці вагові рівняння відрізняються від нормальних

рівнянь лише вільними членами і назвою невідомих. Коефі

цієнти при невідомих у них однакові і мають одну і ту ж

властивість — коефіцієнти, що симетрично розташовані від

носно діагональних квадратичних коефіцієнтів, рівні між со

бою. Через те всі необхідні для визначення вагових коефіці

єнтів Qrs величини можна одержати одночасно з розв’язан

ням нормальних рівнянь, якщо в схемі Гаусса—Дулітля до

дати k додаткових стовлчиків під назвою Qі, Q2, Qz, - • ■, Qa

і виписувати в них замість вільних членів нормальних рів

нянь [а/], [Ы], [сі], [^/] вільні члени вагових рівнянь

згідно з такою таблицею:

Таблиця 41

Вільні члени нормаль

них рівнянь

Вільні члени вагових рівнянь |

<3.

..............

Qk \

[.аі]

- 1

0 0

[Ы\

—1

\c l\

—і

..............

1«1

0 0

- 1 ■

З вільними членами в цих додаткових ставлчиках схеми

при обчисленнях необхідно проробляти ті ж самі операції,

іцо і з вільними членами нормальних рівнянь стовцчика /]. У

наступному параграфі подаємо числовий приклад розв’язання

нормальних рівнянь з одноразовим визначенням вагових кое

фіцієнтів Q.

§ 61. ЧИСЛОВИЙ ПРИКЛАД ВИЗНАЧЕННЯ

ВАГОВИХ КОЕФІЦІЄНТІВ

Обчислення вагових коефіцієнтів розглянемо на конкрет

ному прикладі розв’язання системи трьох нормальних рівнянь

(44,7). Як відомо, в цьому випадку необхідно знайти дев’ять

вагових коефіцієнтів:

Qll, Ql2> Q13»

*?21> Q22> Qs8> (61)1)

Q:i1> Qs2> Q.33>

які визначаються з таких трьох систем вагових рівнянь:

К«] Qn+[e*lQia + [ac] Qir-

1- 0,

[ab] Qlt+[M>]Q13+[to]Q „

- 0,

(61,2)

[ac] Qtl + [H Qia+[cc] Qn

«= 0 j

\aa\ Q21 + [ab] Q22 4- [a.c\ Q3g

«= 0,

\ab]Qu + [bb] Q22+ [be] Qn ~-1 - 0,

(61,3)

[ac[ Qu + [bc] Qn+lcc] QM

[aa] Q31 + [ab] Q33+ [ac] Qn = 0,

fab] Qsi + [bb[Q.t2+[be] QM = 0,

(61,4)

[ac] QS1 + [M Q,3+fcc] Q„-

Для їх розв’язання в схему Гауоса—-Дулітля (табл. 42)

вводимо три додаткові стовпчики під назвами Qx, Qy, QZ| в які

виписуємо вільні, члени рівнянь (61,2), (61,3) і (61,4) від

повідно. Над цими вільними членами проробляємо ті ж самі

операції, що і над вільними членами нормальних рівнянь.

Вагові коефіцієнти визначаються так само, як і невідомі

нормальних рівнянь х, у, г, з тією лише різницею, що при їх

обчисленні замість величин стовпчика І використовуються від

повідні величини СТОВПЧИКІВ Qx, Q:j, Q* .

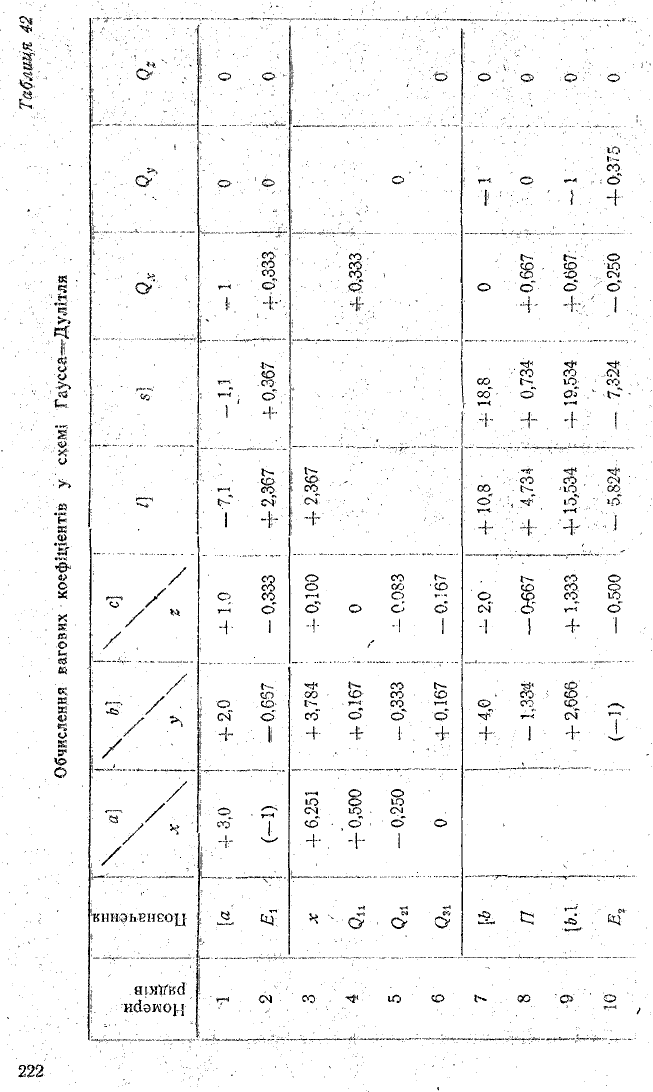
Обчислення вагових коефіцієнтів у схемі Гаусса—Дулітля

а '

й-

о-

о'-

г /

/ *

/ •

•у / .

кшюьенєоц

.ярдакі

И(1эТО|4

СО'

со

- і о

г-н «ГО

tsT сч

О СО

Г-н' О

-I- I

<м

с- t4*- о

СО •

со

'■£> . См

о"

■н-

—

■*зч

«*■

' СО

со сч

00 f-; ю

со

оо

' (С

■ 4-

■■ !

1>.

СО

н-

со

о о

t- rf со

сп

со

<о

со СО

.со

■ У-4' »—>

со

о*' о

-f

о о

о ю

ч-*

СМ Ю •

со - О ' о о

{

н-

_|_

<ч.

4 <5

' с> о?

со

- o '

оо

со

чО

'. ОО

о 'ф to'

г~<

- »о-

■+

'■

■■■- .1

со

Г~ч

о”

-1

©:

со

СО

со

-к ■

.„J

fci