Бухенский К.В., Елкина Н.В., Маслова Н.Н., Ципоркова К.А. Опорные конспекты по высшей математике. Часть 2
Подождите немного. Документ загружается.

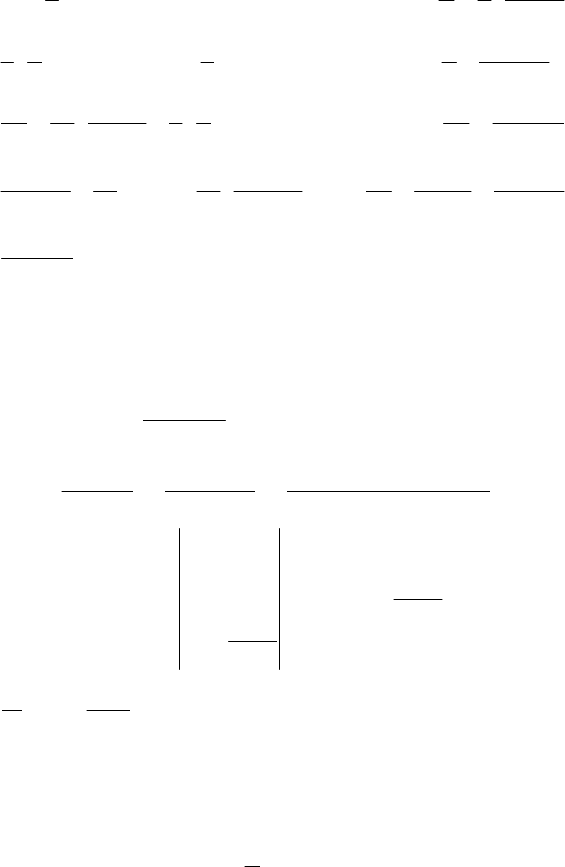
81
()
+⋅−=
∫
−+−=
2
2sin
8
3
8
2cos2cos32cos31
8
1
32
xx
dxxxx
()
(
)
∫
+−=−−
∫
+⋅+
16
2sin3
8
2cos2sin1
8
1
4cos1
2
1
8
3
2
xx
xdxxdxx
(
)
()
+−=
∫
−⋅−⋅++
16
2sin3
16
5
2sin2sin1
2
1
8
1
4
4sin
16
3
16
3
2
xx
xdx
xx
++−=+⋅+−+
64
4sin3
4
2sin
16
5
3
2sin
16
1
2sin
16
1
64
4sin3
3
xxx
C
x
x
x
C
x
++
48
2sin
3
.►
3.
∫
xdxx
nm
cossin . Оба показателя четные, но хотя бы
один из них отрицательный. В этом случае делают замену
x
t tg= .
Пример 6.
∫
x
xdx
4
2
cos
sin
.
◄
(
)
=
∫
+
=
∫
⋅
=
∫
x
dxxxx
x
dxx
x
xdx
4
222
4
2
4
2
cos
cossinsin
cos
1sin
cos
sin
() ()
∫
==
+
∫∫
+=
+
=
=
=
=+= dtt
t
dt
tt
t
dt
dx
tx
tgxt
dxxx
2
2
22
2
22
1
1
1
arctg1tgtg
C
x
C
t
+=+=
3
tg
3
33
.►
5.5. Интегралы вида:
∫
nxdxmx coscos
,
∫
nxdxmxsinsin
,
∫
nxdxmxsincos
, где nm
≠
, вычисляются с помощью формул
тригонометрии:
() ()()
xnmxnmnxmx −++=⋅ coscos
2
1
coscos ,
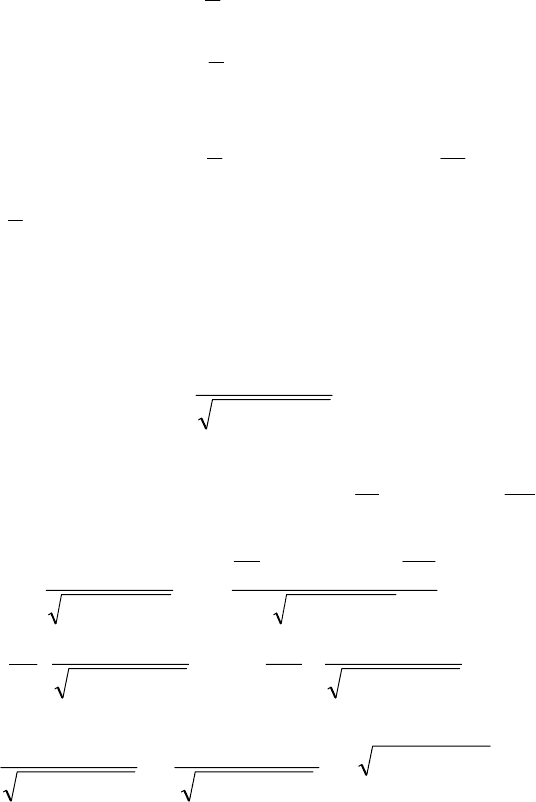
82
() ()()
xnmxnmnxmx +−−=⋅ coscos
2
1
sinsin ,
() ()()
xnmxnmnxmx −++=⋅ sinsin
2
1
cossin .
Пример 7.
∫
⋅
xdxx 2cos5cos .
◄
()
+=
∫
+=
∫
⋅ xdxxxxdxx 7sin
14
1
3cos7cos
2
1
2cos5cos
Cx ++ 3sin
6
1
.►
§ 6. Интегрирование иррациональных функций
Основным методом вычисления интегралов от иррацио-
нальных функций является сведение их к интегралам от рацио-
нальных функций.
6.1. Интегралы вида
∫
++
+
dx
cbxax
NMx
2
.
В первую очередь выделяют в числителе производную зна-
менателя
()
⎟
⎠
⎞
⎜
⎝
⎛
+=
′
++ baxcbxax 2
2
:
()
a
M
b
Nbax
a
M
NMx
2
2
2
−++=+
.
Т.о.,
()
=
∫
++
−++
=
∫
++
+
dx
cbxax
a
Mb
Nbax
a
M
dx
cbxax
NMx
22
2
2
2
()
∫
++
⎟
⎠
⎞
⎜
⎝
⎛
−+
∫
++
+
=
cbxax
dx
a
Mb
N
cbxax
dxbax
a
M
22
2
2
2
.
Первый из полученных интегралов равен:
()
(
)
cbxax
cbxax
cbxaxd
cbxax
dxpax
++=
∫
++
++
=
∫
++
+
2
2
2
2
2
2
.
Для вычисления второго из интегралов сначала выделяем
полный квадрат в знаменателе. С помощью замены переменной
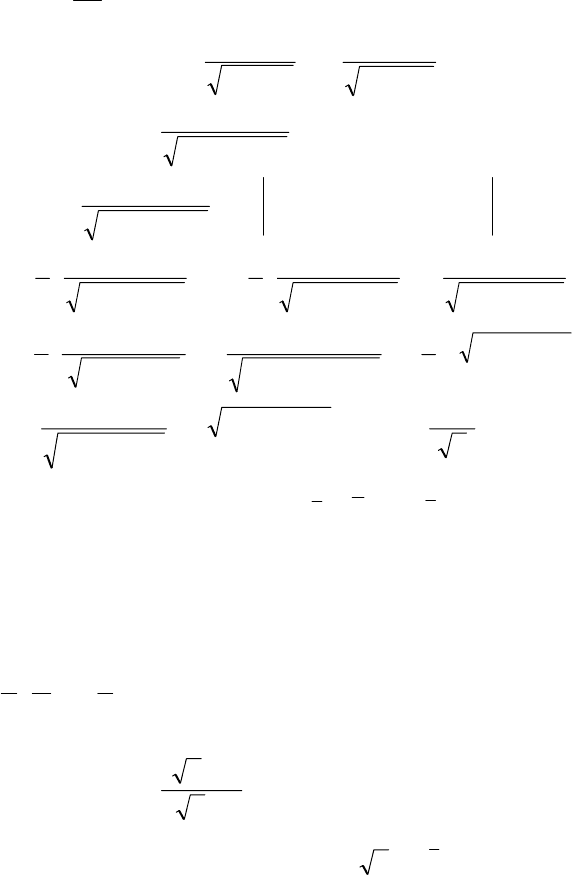
83
a
b
xz
2
+=
второй интеграл приводится к одному из двух таб-
личных интегралов:
∫
±
22
az
dz
,
∫
−
22
za
dz
.
Пример 1.
∫
−−
+
dx
xx
x
2
26
4
.
◄
(
)
=−−=
′
−−=
∫
−−
+
xxxdx
xx
x
2226
26
4
2
2
(
)
=
∫
−−
+
∫
−−
−
−
−=
∫
−−
−
−−
−=
222
26
3
26
22
2
1
26
622
2
1
xx
dx
xx
dxx
dx
xx
x
(
)
()
+−−⋅−=
∫∫
++−
+
−−
−−
−=
2
22
2
262
2
1
127
3
26
26
2
1
xx
xx
dx
xx
xxd
()
C
x
xx
x
dx
+
+
+−−−=
∫
+−
+
7
1
arcsin326
17
3
2
2
.►
6.2. Интеграл вида
∫
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
dxxxxxR
s
h
q
p
r
k
,,,, K ,
где
Z
∈
sqprk ,,,,, K . Для вычисления интеграла используется
замена:
n
tx = , где n – наименьшее общее кратное чисел
sq
r
,,, K
(иначе: n – наименьший общий знаменатель дробей
s
h
q
p
r
k
,,,
K ). Тогда dtntdx
n 1−
= . В результате подстановки
получим интеграл от дробно-рациональной функции.
Пример 2.
∫
−
−
dx
xx
x
2
1
.
◄ Интеграл зависит от
x
и от
2
1
xx = , поэтому приме-
ним подстановку:
2
tx = .
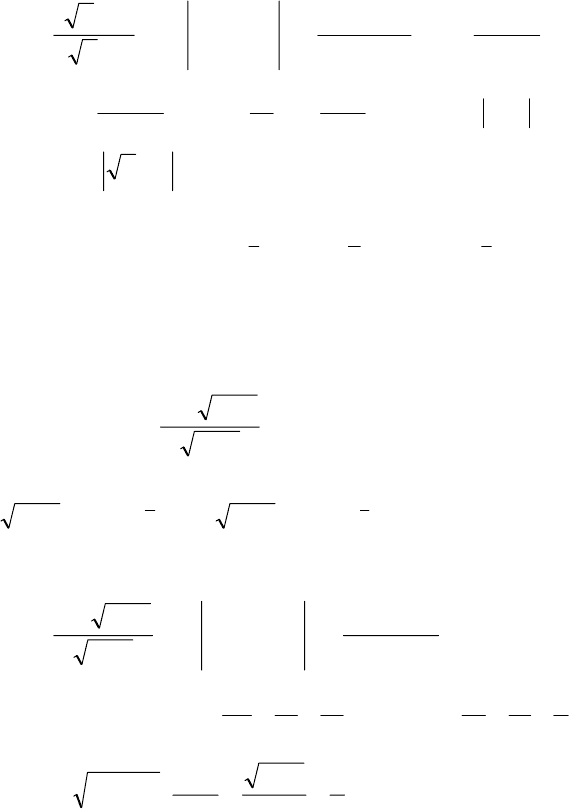
84
(
)
=
∫∫
−
−
−=
−
−
=
=
=
=
∫
−
−
dt
tt
tt
tt
tdtt
tdtdx
tx
dx
xx
x
2
2
2
21
2
2
1
2
2
2
2
∫∫
=+−−−=
−
−−=
⎟
⎠
⎞
⎜
⎝
⎛
−
+−= Ctt
t
dtt
dt
tt
t
2ln2
2
2
2
2
2
12
2
2
2
Cxx +−−−= 2ln2 .►
6.3. Интеграл вида
()()()
dxbaxbaxbaxxR
s
h
q
p
r
k
∫
⎥
⎦
⎤
⎢
⎣
⎡
+++
,,,, K ,
где
Z
∈
sqprk ,,,,, K . Для вычисления интеграла используется
замена:
n
tbax =+ , где n – наименьшее общее кратное чисел
sq
r
,,, K .
Пример 3.
dx
x
xx
∫
+
++
3
1
1
.
◄ Подынтегральное выражение зависит от
()
2
1
11 +=+ xx
и
()
3
1
3
11 +=+ xx
. Наименьшим общим
кратным чисел 2 и 3 является число 6, поэтому применим заме-
ну:
6
1 tx =+
.
=
∫
+−
=
=
=+
=
∫
+
++
dtt
t
tt
dttdx
tx
dx
x
xx
5
2
36
5
6
3
6
1
6
1
1
1
()
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+=+
∫
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+=−+=
4
1
710
6
4710
66
36
4
4710
369
tt
tC
ttt
dtttt
()
C
xx
xC +
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
+
+
+=+
4
1
7
1
10
1
16
3
2
.►
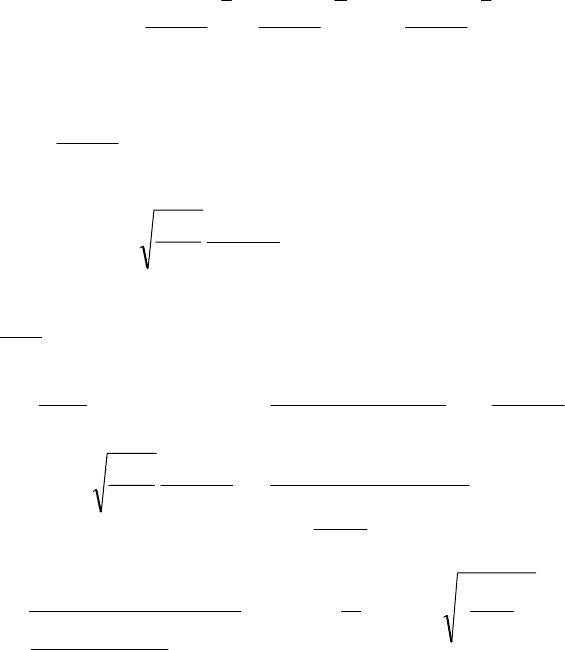
85
6.4. Интеграл вида
dx
dcx
bax
dcx
bax
dcx
bax
xR
s
h
q
p
r
k
∫
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
+
+
⎟
⎠
⎞
⎜
⎝
⎛
+
+
⎟
⎠
⎞
⎜
⎝
⎛
+
+
,,,, K
,
где
Z
∈
sqprk ,,,,, K . Для вычисления интеграла используется
замена:
n
t
dcx
bax
=
+
+
, где n – наименьшее общее кратное чисел
sq
r
,,, K
.
Пример 4.
()
∫
−
−
+
2
1
1
1
x
dx
x
x
.
◄ Для нахождения интеграла воспользуемся заменой
2
1
1
t
x
x
=
−
+
. Выразим
x
:
(
)
⇒−=+⇒−=+ 111
2222
ttxxttx
1
1
2
2
+
−
=⇒
t
t
x
. Найдем dx :
(
)
(
)
() ()
2
2
2
2
22
1
4
1
1212
+
=
+
−−+
=
t
tdt
dt
t
tttt
dx
.
Тогда
()
()
=
∫
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−
−
⋅
=
∫
−
−
+
2
2
2
2
2
2
1
1
1
1
4
1
1
1
t
t
t
tdtt
x
dx
x
x
()
()
()
.
1
1
3
1
1
11
4
3
3
2
2
2
2
2
2
22
2
C
x
x
C
t
dtt
t
t
tt
dtt
+
⎟
⎠
⎞
⎜
⎝
⎛
−
+
==+==
+
+
+−+
=
∫∫
►
6.5. Если подынтегральное выражение представляет собой
дифференциальный бином, то есть имеет вид
(
)
dxbxax
p
nm
+ ,
где
Q∈pnm ,, , то данный интеграл сводится к интегралу от
рациональной дроби в следующих трех случаях (подстановки
П.Л. Чебышева):
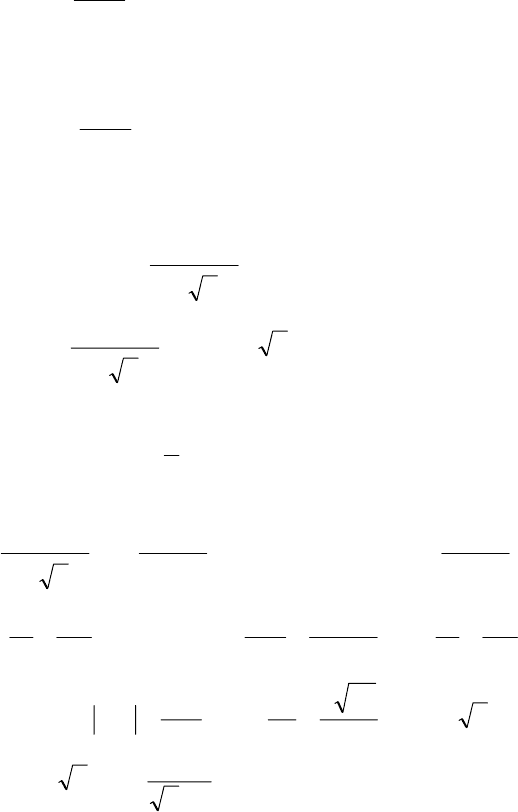
86
1) Z∈p ; тогда интеграл можно рационализовать с помо-
щью подстановки
k
tx = , где k – наименьший общий
знаменатель дробей
m и n ;
2)
Z∈
+
n
m 1
; тогда интеграл рационализуется с помощью
подстановки
kn
tbxa =+
, где k – знаменатель числа
p
;
3)
Z∈
⎟
⎠
⎞
⎜
⎝
⎛
+
+
p
n
m 1
; в этом случае рационализация дости-
гается подстановкой
kn
tbxa =+
−
, где k – знамена-
тель числа
p
.
Пример 5.
()
∫
+
2
2
1 x
dxx
.
◄
()
()
dxxx
x
dxx
2
2
2
2
1
1
−
+
∫
=
∫
+
.
Так как
2
−
=
p , имеем случай 1. Применим замену:
2
tx = (
2
1
,2 == nm
, наименьший знаменатель этих чисел
2=k
). Тогда
tdtdx 2
=
.
()
() ()
=
∫
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
+−+−=
∫
+
=
∫
+
dt
t
t
ttt
t
dtt
x
dxx
2
23
2
5
2
2
1
45
4322
1
2
1
()
∫
−+−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−
+
+−+−=
2
34
2
2
34
3
3
4
2
1
1
1
5
283
3
4
2
t
tt
dt
t
t
tt
tt
+−+−=+
+
+++− xx
xx
C
t
tt 83
3
4
21
2
1ln108
32
()
C
x
x +
+
+++
1
2
1ln10
.►
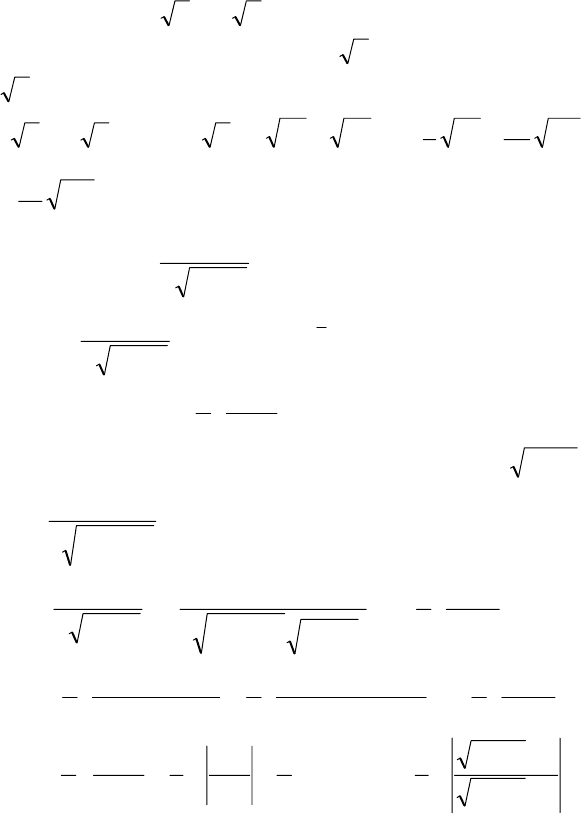
87
Замечание 1. При N
∈
p интеграл от дифференциального
бинома приводится к интегралам от степенных функций путем
возведения в степень и раскрытия скобок.
Пример 6.
(
)
dxxx
2
3
2
∫
+
.
◄
2=p . Возведем сумму
3
2 x+ в квадрат и умножим на
x . Тогда
()
(
)
++=
∫
++=
∫
+
6
113
6
7
6
5
2
3
11
24
3
8
442 xxdxxxxdxxx
Cx ++
6
13
13
6
.►
Пример 7.
∫
+
4
3
1 xx
dx
.
◄
()
∫
+=
∫
+
−
−
dxxx
xx
dx
4
1
31
4
3
1
1
,
0
1
,
4
1
,3,1 =
+
−==−=
n
m
pnm
– целое число. Имеем случай
2). Делаем подстановку:
43
1 tx =+ . Тогда
3
4
1−= tx и
()
dt
t
t
dx
3
2
4
3
13
4
−
=
. В результате интеграл примет вид:
()
∫
=
−
=
∫
−−
=
∫
+
1
3
4
113
4
1
4
2
3
4
3
2
4
3
4
3
t
dtt
dt
ttt
t
xx
dx
()()
(
)
(
)
()()
+
∫
−
=
∫
+−
−++
=
∫
+−
=
1
3
2
11
11
3
2
11
2
3
2
222
22
22
2
t
dt
dt
tt
tt
tt
dtt
+
++
−+
=++
+
−
=
+
+
∫
11
11
ln
3
1
arctg
3
2
1
1
ln
3
1
13
2
4
3
4
3
2
x
x
Ct
t
t
t
dt
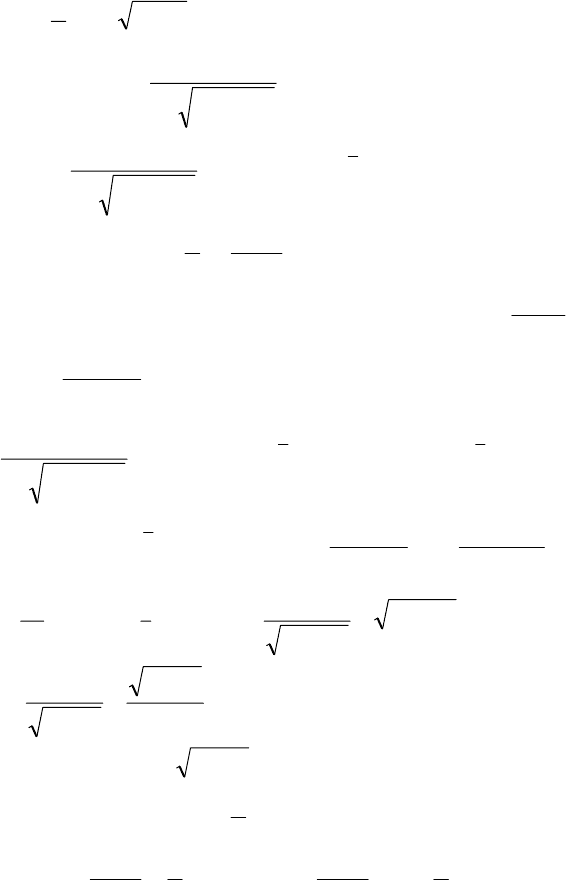
88
Cx +++
4
3
1arctg
3
2
.►
Пример 8.
()
∫
+
3
22
1 xx
dx
.
◄
()
()
∫
+=
∫
+
−
−
dxxx
xx
dx
2
3
22
3
22
1
1
,
Z∈−=+
+
−==−= 2
1
,
2
3
,2,2 p
n
m
pnm . Имеем случай 3).
Делаем подстановку:
22
1 tx =+
−
. Откуда
1
1
2
2
−
=
t
x
и
()
2
2
1
2
2
−
−
=
t
tdt
xdx
. Преобразуем интеграл:
()
() ()
∫
=+=
∫
+=
∫
+
−
−
−−
−
−
dxxxxdxxx
xx
dx
3
2
3
22
2
3
22
3
22
11
1
() ()
()
(
)
=
∫
−
−=
∫
−
−
−
∫
=+=
−
−
−−
2
2
2
2
3
3
2
2
3
26
1
1
11
t
dtt
t
tdt
ttxdxxx
=++−
+
−=+−−=
∫
−
∫
=
−
−
Cx
x
Ct
t
dt
t
dt
2
2
2
1
1
11
C
x
x
x
x
+
+
−
+
−=
2
2
1
1
.►
Пример 9.
dxxx
∫
+
42
1 .
◄
2
1
,4,2 === pnm
– не целое число, первый случай не
подходит,
4
31
=
+
n
m
– не целое и
4
51
=+
+
p
n
m
– не целое, по-
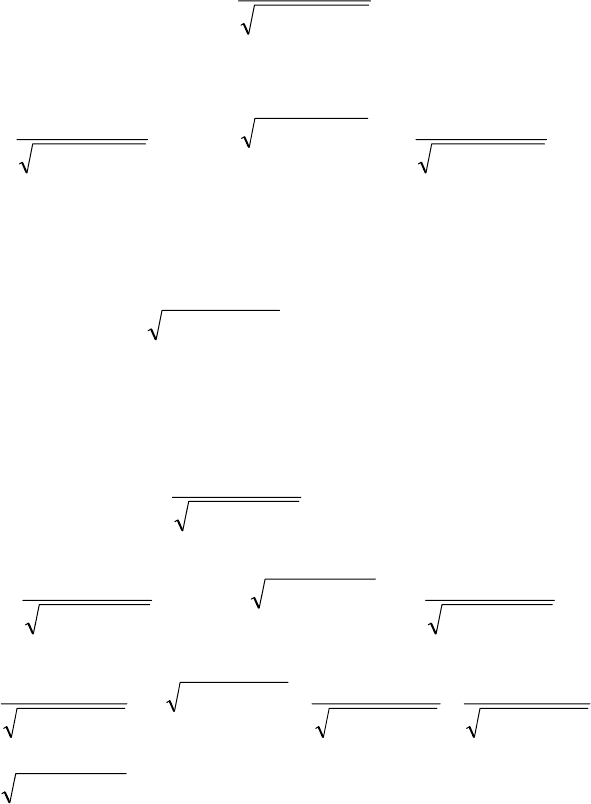
89
этому второй и третий случаи не подходят тоже. Интеграл не
может быть выражен через элементарные функции.►
6.6. Интеграл вида
(
)
∫
++ cbxax
dxxP
n
2
, (4)
где
()
01
1
1
axaxaxaxP
n
n
n
nn
++++=
−
−
K
.
Применяется формула:
()
()
∫
++
+++=
∫
++
−
cbxax
dx
cbxaxxQ
cbxax
dxxP
n
n
2
2
1
2
λ
, (5)
где
()
01
2
2
1
11
bxbxbxbxQ
n
n
n
nn
++++=
−
−
−
−−
K .
Чтобы найти коэффициенты
λ
,,,,,
0121
bbbb
nn
K
−−
, запи-
сывают для интеграла (4) равенство (5) с неопределенными ко-
эффициентами и дифференцируют его. Полученное выражение
умножают на
cbxax ++
2
. Тем самым освобождаются от
дробей и корней. Затем приравнивают коэффициенты при оди-
наковых степенях
x
в левой и правой частях равенства. Решая
полученную систему, находят коэффициенты
λ
,,,,,
0121
bbbb
nn
K
−−
.
Пример 10.
(
)
∫
++
+
22
1
2
2
xx
dxx
.
◄ По формуле (5) получим равенство:
(
)
()
∫
++
++++=
∫
++
+
22
22
22
1
2
2
2
2
xx
dx
xxbax
xx
dxx
λ
. (6)
Дифференцируем его:
(
)
(
)
2222
1
22
22
1
22
2
2
2
++
+
++
++
+++=
++
+
xxxx
xbax
xxa
xx
x
λ
.
Умножим обе части последнего равенства на
22
2
++ xx :
(
)
(
)
(
)
λ
++++++=+ 1221
22
xbaxxxax
.
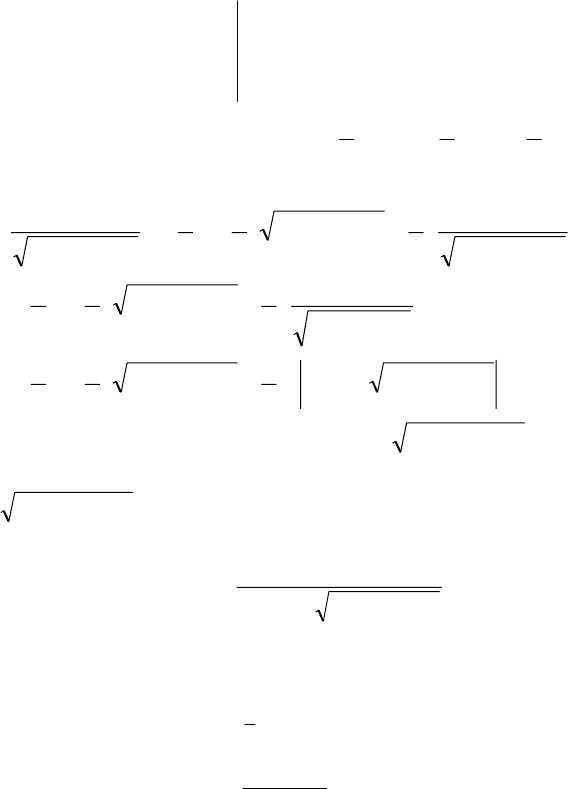
90
Приравниваем коэффициенты при одинаковых степенях
x
слева и справа:
.21
,30
,21
0
1
2
λ
++=
+=
=
ba
ba
a
x
x
x
Решая систему, находим
2
3
,
2
3
,
2
1
=−==
λ
ba
. Под-
ставляем найденные коэффициенты в (6):
(
)
=
∫
++
+++
⎟
⎠
⎞
⎜
⎝
⎛
−=
∫
++
+
22
2
3
22
2
3
2
1
22
1
2
2
2
2
xx
dx
xxx
xx
dxx
(
)
()
=
∫
++
+
+++
⎟
⎠
⎞
⎜
⎝
⎛
−=
11
1
2
3
22
2
3
2
1
2
2
x
xd
xxx
Cxxxxxx ++++++++
⎟
⎠
⎞
⎜
⎝
⎛
−= 221ln
2
3
22
2
3
2
1
22
.►
Замечание 2. Интеграл вида
()
dxcbxaxxP
n
∫
++
2
при-
водится к интегралу (4) умножением и делением на
cbxax ++
2
.
6.7. Интеграл вида
(
)
()
∫
++− cbxaxx
dxxP
m
n
2
α
, (7)
где
()
xP
n
– многочлен степени n . Возможны два случая:
1)
mn < . Интеграл приводится к виду (4) с помощью под-
становки
t
x
1
=−
α
;
2)
mn ≥ . У дроби
(
)
()
m
n
x
xP
α
−
выделяется целая часть, по-
сле чего получаем интегралы вида (4) и (7) в случае
mn < .
