Carlip S. Quantum Gravity in 2+1 Dimensions

Подождите немного. Документ загружается.

Classical general relativity

2+1 dimensions

and

it is

easy

to see

that

the

variation

G[p,r] induces

boundary

variation

-2

f #

[paSco^

+ Tade^)

+....

(2.104)

in the

ADM case,

must cancel this expression

adding

new

boundary term

this case

G[p,t]

= 2

/ #

(pacof

ef)

(2.105)

We shall see

the next chapter that this boundary term gives the same

conserved charges

the

total mass

and

angular momentum

as the

corresponding ADM expression.

We can now express the ADM constraints

and Jf \

terms

the

first-order constraints

and

should expect

the

results

to be

somewhat ambiguous: the first-order formalism has more symmetries (lo-

cal Lorentz transformations as well as diffeomorphisms), and consequently

more constraints, than the ADM formalism. To avoid this ambiguity, we

shall derive

the

ADM constraints only modulo local Lorentz transfor-

mations; that

is to

say,

shall find

a set of

constraints that obey

the

algebra (2.47)-(2.48),

but

only

up to

terms proportional

the generator

local

(2,1) transformations.

For simplicity, let us set the cosmological constant A to zero. We saw in

the last section that

diffeomorphism generated by

vector

£*

is equivalent

ISO (2,1) transformation with

= ^ef,

plus

local Lorentz

transformation, which we are ignoring. We might therefore expect that

^Jft

, (2.106)

2ei

. (2.107)

The Hamiltonian constraint

Jf is a

bit harder

guess, but the answer

known from work on Ashtekar's formulation of (3+l)-dimensional gravity

[11]:

Jf =

Ig-^e^ehf^,

(2.108)

where

g is

the determinant

the spatial metric,

det(«,%). (2.109)

The form

this constraint can be made plausible by noting that

bc€

fl6c

% V

2ee°

2NJge°

, (2.110)

so equation (2.108)

rather closely parallel

equation (2.15).

2.7 Comparing generators of

invariances

A tedious but straightforward calculation now shows that the generators

(2.107) and (2.108) have the correct Poisson brackets (2.47)-(2.48), modulo

terms proportional to

€

We have thus constructed the constraint algebra

of general relativity from that of a gauge theory. The existence of such

a construction was first noted by Bengtsson, and it provides yet another

viewpoint from which to understand the simplicity of (2+l)-dimensional

gravity: the difficult diffeomorphism constraints reduce to much simpler

gauge constraints [35].

It is easy to see how the dimensionality of spacetime has entered this

construction: we have made explicit use of the Levi-Civita tensor, whose

form depends on the number of dimensions. In 3+1 dimensions, much

of the simplicity found here is lost. Nevertheless, a related construction

has been used to show that even in 3+1 dimensions, the phase space of

general relativity 'embeds' in the phase space of a gauge theory; this is

the structure that provides much of the power of Ashtekar's new variables

A field guide to the (2+l)-dimensional

spacetimes

In the last chapter, we investigated two formulations of the vacuum

Einstein field equation in 2+1 dimensions. In this chapter, we will solve

these field equations in several fairly simple settings, finding spacetimes

that represent a collection of point particles, a rotating black hole, and a

variety of closed universes with topologies of the form

[0,1]

xZ. In contrast

to (3+l)-dimensional general relativity, where it is almost always necessary

to impose strong symmetry requirements in order to find solutions, we

shall see that for simple enough topologies, it is actually possible to find

the

general

solution of the (2+l)-dimensional field equations.

The reader should be warned that this chapter is not a comprehensive

survey of solutions of the (2+l)-dimensional field equations. In particular,

I will spend a limited amount of time on the widely studied point particle

solutions, and I will say little about solutions with extended ('string')

sources and solutions in the presence of a nonvanishing matter stress-

energy tensor. The latter are of particular interest for quantum theory

- they offer models for studying the interaction of quantum gravity and

quantum field theory - but systematic investigation of such solutions has

only begun recently, and they are not yet very well understood.

3.1 Point sources

As a warm-up exercise, let us use the ADM formalism of chapter 2 to

find the general stationary, axisymmetric solutions of the vacuum field

equations with vanishing cosmological constant [90]. Such spacetimes are

the (2+l)-dimensional analogs of the exterior Schwarzschild and Kerr

metrics, representing the region outside a circularly symmetric gravitating

source. These spacetimes have a possible (3+l)-dimensional interpretation

as well: as described in chapter 1, the sources can be viewed as cross-

sections of straight cosmic strings.

3.1 Point

sources

A general stationary, axisymmetric (2+l)-dimensional metric can be

written in the form

= -N(r)

+ f(r)

+ r

(# - N*(r)dt)

, (3.1)

where I have used a spatial coordinate transformation to set the coefficient

d(j)

to be r

. Physically, this coordinate choice means that a circle of

constant r has circumference 2nr. The spatial metric gy is simply

The only nonvanishing component is thus

X i

—

(N^V

and the corresponding canonical momentum is

and an easy calculation shows that

~ f

and hence

^J^g

{2)

= 2^ (3.4)

Since the metric is static, the extrinsic curvature is

Tj).

(3.5)

Let us first evaluate the momentum constraint (2.14),

y = 0 = g%v*i - \zt

)ni

Since g^ has only diagonal elements and n^

is entirely off-diagonal, the

last term of (3.8) vanishes. Hence n^ is a constant,

V = A. (3.9)

40 3 Afield

guide

to the (2+l)-dimensional

spacetimes

We next consider the Hamiltonian constraint (2.13), which becomes

= 0. (3.10)

The solution of this equation is

1 A

where B

is another integration constant, which must be positive to ensure

that f

remains positive for large values of r.

To proceed further we shall also need one of the dynamical equations

of motion coming from varying g

in the action (2.12). To find the

appropriate equation, we substitute the ansatz (3.1) for the metric into the

action* and vary /. The Hamiltonian constraint is

= zjr(n

)

—

2-72, \3-H)

the

momentum constraint

independent

of /, and all

time derivatives

vanish,

the

action

<t>

o /'I

I dr

< 2Nrf(ir

)

—

2iV-^

terms independent

of f.

* > (3.13)

The field equation obtained by varying / is thus

^ +

Nrin^)

= 0. (3.14)

Combining (3.12) and (3.14) and the constraint

Jtf*

= 0, we see that

N = f-

{

(3.16)

up to a constant factor that can be absorbed by a suitable rescaling of

the time coordinate t.

This procedure is a bit dangerous: by fixing an ansatz, we are restricting the possible

variations of the metric, and hence finding only the metrics that are extrema within a

limited class of geometries. In general we are not guaranteed that our solutions are

extremal under variations that take the metric outside this class. Here, however, the

ansatz is completely determined by symmetry considerations, and we should find any

extrema with the appropriate symmetries.

3.1 Point

sources

To complete our solution, we can now use (3.7) to determine N^:

We may further restrict our attention to solutions for which C = 0, since

otherwise the metric has unphysical asymptotic behavior.

Substituting (3.11), (3.16) and (3.18) into (3.1), we

finally

obtain a metric

This metric can be put into a slightly more standard form by defining a

new radial coordinate

and by rescaling the time coordinate by a factor of

to finally obtain

= -(dt - 4#)

+ ^

d(j)

(3.21)

To interpret the geometry of this spacetime, let us first consider the

static case, ,4 = 0. The line element (3.21) can then be made into the

standard flat metric through the coordinate transformation

cj)

_•

</>'

Be/).

(3.22)

This is to be expected, since we saw in chapter 1 that the field equations

require the curvature to vanish. Note, however, that <// does not have the

standard periodicity: as 0 varies from 0 to 2n,

(/)'

varies from 0 to 2n

—

/?,

where

fi =

2n(l-B).

(3.23)

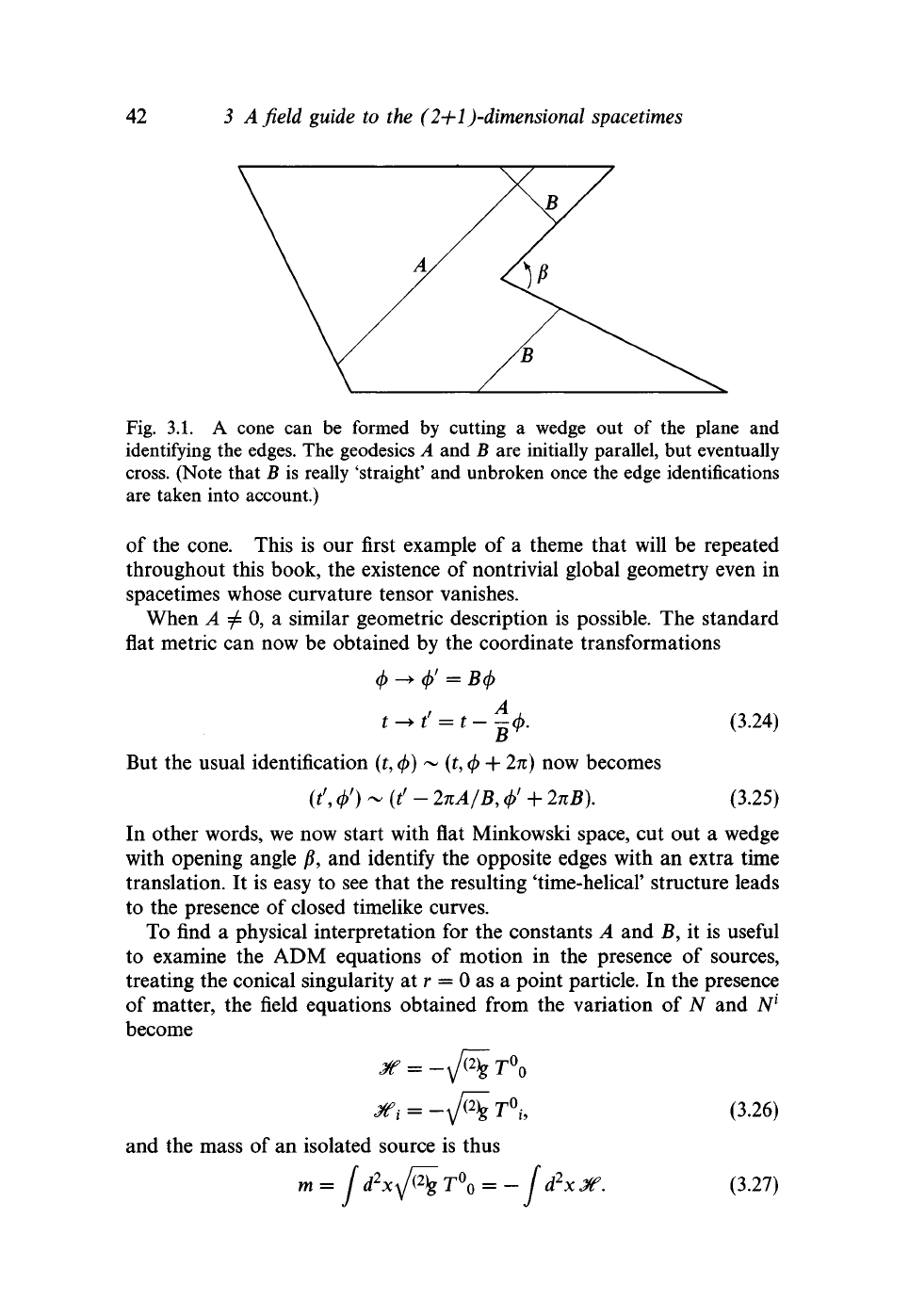
For 0 < P < 27i, the spatial metric is actually that of a cone, obtained

by cutting a wedge of opening angle /J out of the plane and identifying

the two edges (see figure 3.1). The angle /} is known as the deficit angle

Afield guide

to the

(2+l)-dimensional spacetimes

Fig. 3.1. A cone can be formed by cutting a wedge out of the plane and

identifying the edges. The geodesies A and B are initially parallel, but eventually

cross.

(Note that B is really 'straight' and unbroken once the edge identifications

are taken into account.)

the

cone. This

is our

first example

of a

theme that will

repeated

throughout this book,

the

existence

nontrivial global geometry even

spacetimes whose curvature tensor vanishes.

When

A ^ 0, a

similar geometric description

possible.

The

standard

flat metric

can now be

obtained

by the

coordinate transformations

t^t' =

t-^cj>.

(3.24)

But the usual identification (t,

(/>)

~ (t,

<\>

+ 2n) now becomes

(£',

<t>')

~ (t

2nA/B,

</>'

+ 2nB).

(3.25)

In other words,

we now

start with flat Minkowski space,

cut out a

wedge

with opening angle

j8, and

identify

the

opposite edges with

extra time

translation.

It is

easy

to see

that

the

resulting 'time-helical' structure leads

the

presence

closed timelike curves.

To find

physical interpretation

for the

constants

A and B, it is

useful

to examine

the ADM

equations

motion

in the

presence

sources,

treating

the

conical singularity

at r = 0 as a

point particle.

In the

presence

of matter,

the

field equations obtained from

the

variation

of N and N

become

(3.26)

and

the

mass

of an

isolated source

thus

= I

x^Mg

T°

= -

Jt.

(3.27)

3.1 Point

sources

The only term in the Hamiltonian constraint (3.10) that has a chance of

behaving peculiarly at r = 0 is the spatial curvature ^R. Indeed, recall

from section 4 of chapter 2 that the curvature can be written in the form

[ d(j)v

= 2nv\ (3.28)

where it is evident from (3.4) that

= --+ const. ~ -IB + const. (3.29)

as r -•

oo.

We can fix the constant by noting that when B = 1 and A = 0,

the metric gy is that of flat Euclidean two-space, for which the integral

(3.28) must vanish. Hence

= 2-2B = ^-, (3.30)

and the total curvature integral is 2/?. Restoring factors of G, equation

(3.27) thus becomes

m =

A similar analysis can be applied to the angular momentum of the

source, which in asymptotically Cartesian coordinates is

/'•= fd

x(x

T°J-xJT

)=2 f ^(x'V-xV-'V

J V

(3.32)

where I have used the momentum constraints to write T°

in terms of

Setting

j^j***

(3.33)

near infinity, we see that

sbs*

(334)

so A/B is a measure of the angular momentum of the source.

The reader may be uncomfortable with these arguments, based as they

are on an analysis that is at least superficially noncovariant. Fortunately,

the interpretation of the integration constants A and B may be checked

in a manifestly covariant manner by calculating the conserved charges of

chapter 2 associated with rotations and time translations at infinity. We

44 3 Afield

guide

to the (2+l)'dimensional

spacetimes

have already computed the quantity v

- appearing in (2.56); combining

this result with the expression (3.9) for the canonical momentum, we see

that the total boundary diffeomorphism generator is

= ^

d<j>

[(2

2B)l + 7AI+], (3.35)

where I have again restored the constants.

In particular, a diffeomorphism that is asymptotically a time translation

has £ = 1, giving # = (}/$nG. We thus confirm that /? is the conserved

quantity associated with time translations at spatial infinity, that is, the

mass.

Similarly, an asymptotic rotation is described by |* = 1 and

\ = A/B. (The time translation component reflects the 'time-helical'

structure of the metric, and is chosen so that the coordinate f in (3.24) is

left invariant.) The associated charge is then # = A/4GB, which is thus

the angular momentum, the conserved quantity associated with rotations

at infinity. Equivalent expressions for the mass and angular momentum

may be found by computing the quasilocal mass of Brown and York

associated with a surface at infinity [43].

The mass and angular momentum, constructed as integrals at spatial

infinity, are the (2+l)-dimensional analogs of the ADM mass and an-

gular momentum in standard general relativity. Similar integrals exist

for any isolated system of sources. Note, however, that because of the

asymptotically conical structure of our solutions, there are no asymptotic

symmetries representing spatial translations or boosts, and thus no analog

of the full ADM momentum vector. One way to understand this is to

observe that while the metric (3.21) admits local solutions of the Killing

equation corresponding to the full Poincare group, most of the resulting

would-be Killing vectors are not preserved under the identifications (3.25);

only the Killing vectors corresponding to rotations and time translations

are globally defined.

It is also instructive to examine the conserved charges in the first-order

formalism. A suitable triad for the metric (3.21) is

e°

= dt-

(A/B)d</>

=df

(3.36)

and it is easily checked that the only nonvanishing component of the spin

connection (2.63) is

co°

-Bdcj),

(3.37)

for which the field equations (2.62) and (2.65) are clearly satisfied. There

3.2

The

(2+l)-dimensional

black hole

are now two candidates for asymptotic symmetries, that is, gauge trans-

formations that leave the frame and spin connection fixed at infinity:

p° - 1, (3.38)

corresponding to a time translation, and

T°~-1,

~r, (3.39)

corresponding to a spatial rotation. For the time translation (3.38), the

generator (2.105) is (? = 2/J

—

4TC,

in agreement with the ADM result up

to an overall additive constant. Similarly, for the rotation (3.39), we find

G = 4nA/B, again coinciding with the ADM result.

The analog of the metric (3.21) for a system of stationary, spinning

sources is also known [78]. In 'Cartesian' coordinates, the metric for

a collection of point particles with masses M

and spins J

located at

positions a

/ (3.40)

In contrast to the (3+l)-dimensional case, this is an exact stationary

solution for multiple sources. The existence of such a solution reflects

the peculiar weak-field limit discussed in chapter 1: stationary sources

experience no Newtonian interaction. Moving sources, on the other hand,

experience nontrivial scattering, as one would expect from the conical

nature of the metric. Figure 3.1, for example, shows two initially parallel

geodesies on a conical background; it is evident that they are 'scattered'

as they pass the apex of the cone, intersecting each other at the far

side.

There has been considerable work on the structure of spacetimes

representing moving sources in 2+1 dimensions, which I will not discuss

here;

see, for example, reference [34] for an interesting treatment.

3.2 The (2+l)-dimensional black hole

The axially symmetric spacetimes of the last section become even more

interesting in the presence of a negative cosmological constant A =

—I//

for which spacetime is asymptotically anti-de Sitter. Most of the preceding

derivation can be repeated, with a few changes:

The Hamiltonian constraint (3.10) is now