Casing/Tubing design manual october 2005 Chevron
Подождите немного. Документ загружается.

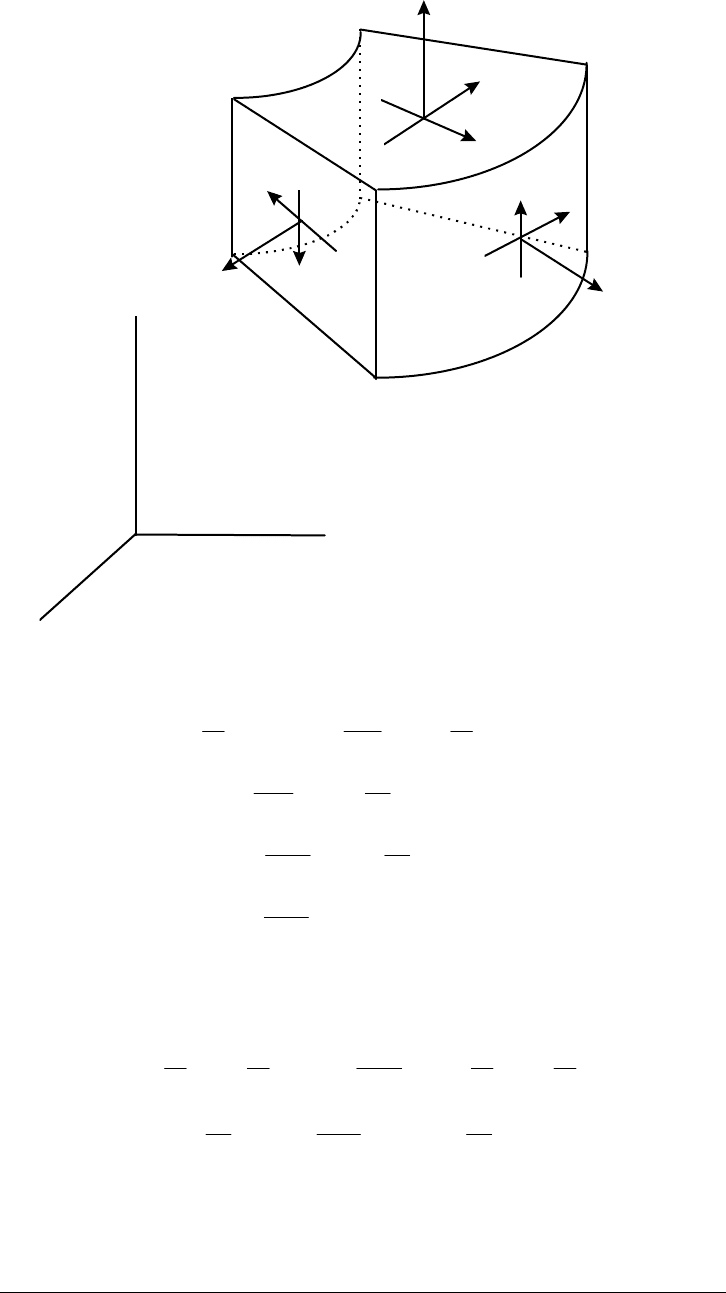
X
Y
Z
σ
θ
σ
θz
σ
θr
σ
r
+
∂
σ
r
/
∂
r dr
σ
rθ
+
∂
σ
rθ
/
∂
r dr
σ
rz
+
∂
σ
rz
/
∂
r dr
σ
zθ
+
∂
σ
zθ
/
∂
z dz
σ
zr
+
∂
σ
zr
/
∂
z dz
σ
z
+
∂
σ
z
/
∂
z dz
Figure D-4. Equilibrium of a Differential Element Centered at (r, θ, z)
−−
⎛
⎝
⎜
⎞
⎠
⎟
++
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
+− − −
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
+− + +
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
+− + +
⎛
⎝
⎜
⎞
⎠
⎟
+=
σθσ
∂σ
∂
θ
σσ
∂σ
∂θ
θ
θ
σσ
∂σ
∂θ
θ
θ
σσ
∂σ
∂
θχ θ
θθ
θ
θθ
θ
rr
r
rr
r
zr zr
zr
r
r
dr
ddz
r
dr r
dr
ddz
d
d
drdz
d
d
drdz
z
dz rdrd rdrd dz
22
2
2
0
sin
cos
(D-30)
and in the
-direction, moment equilibrium about the center of the element is
expressed as:
z
()
[]
()
σθσ
∂σ
∂
θ
σ
θ
σ
∂σ
∂θ
θ
θ
θθ
θ
θθ
θ
rr
r
rr
r
r
dr
ddz
dr
r
dr r
dr
ddz
dr
drdz r
d
ddrdzr
d
−
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
++
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
−−+
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
=
22 22
22
0
(D-31)
Rearranging equations (D-30) and (D-31), factoring the common factor (drd
θ
dz),
using the small angle approximations (
sin , cos ,
θ
θ
θ
θ
≅
≅
<
<1for 1
), and ignoring
higher order terms, the final forms of these equations can be written:
D-12 Casing/Tubing Design Manual
October 2005

∂σ
∂
∂
σ
∂θ
∂σ
∂
σ
σ
χ
θθ
r
r
zr
r
r
rr z r
+++
−
+=
1
0 (D-32)
σ
σ
θθ
rr
=
(D-33)
where the required result of moment equilibrium is symmetry of the shear stress
components. Force equilibrium requirements in the
θ
and directions yield
respectively,
z
∂
σ
∂
∂
σ
∂θ
∂
σ
∂
σ
χ
θθθθ
θ
rzr
rr z r
++++
1
2
0=
(D-34)
∂σ
∂
∂σ
∂θ
∂σ
∂
σ
χ
θ
rz
z
zrz
z
rr z r
++++
1
0=
(D-35)
and the moment equilibrium equations in the
and r
θ
directions yield
respectively,
σ
σ
σ
σ
θθ
z z rz zr
=
=
, (D-36)
D.3.3 Special Cases
As was the case with the strain-displacement relations, it is convenient to
consider certain useful simplifications to equations (D-32), (D-34), and (D-35).
However, because of the inter-relationship between stress and strain via the
material properties, it will be necessary to postpone a discussion of these special
cases until the constitutive equations have been introduced.
D.4 Stress-Strain Relations
The concepts of both stress and strain are independent of the material under
consideration. In order to relate the response (strain) to the loading (stress), it is
necessary to introduce additional parameters characterizing the particular
material being studied. The resulting expressions are termed constitutive
relations since their exact form will depend on the constitution of the material.
A given set of constitutive relations will be applicable only over a certain range of
conditions. For example, the equations relating stress and strain (rate) for water
at atmospheric pressure are only valid below 100
°C (212°F). Above that
temperature, a phase change occurs (water
→steam) and a new set of stress-
strain rate relations applies.
A similar phenomenon occurs with tubular steel. Below a certain stress state,
steel may be classified as an elastic material with corresponding elastic stress-
strain relations. Above a certain stress state, the physical properties of steel
change and the steel are characterized as an elastic-plastic material. Above this
critical stress state, referred to as yield, it is necessary to formulate a new set of
equations to describe the response of the steel to external loads.
Casing/Tubing Design Manual D-13
October 2005
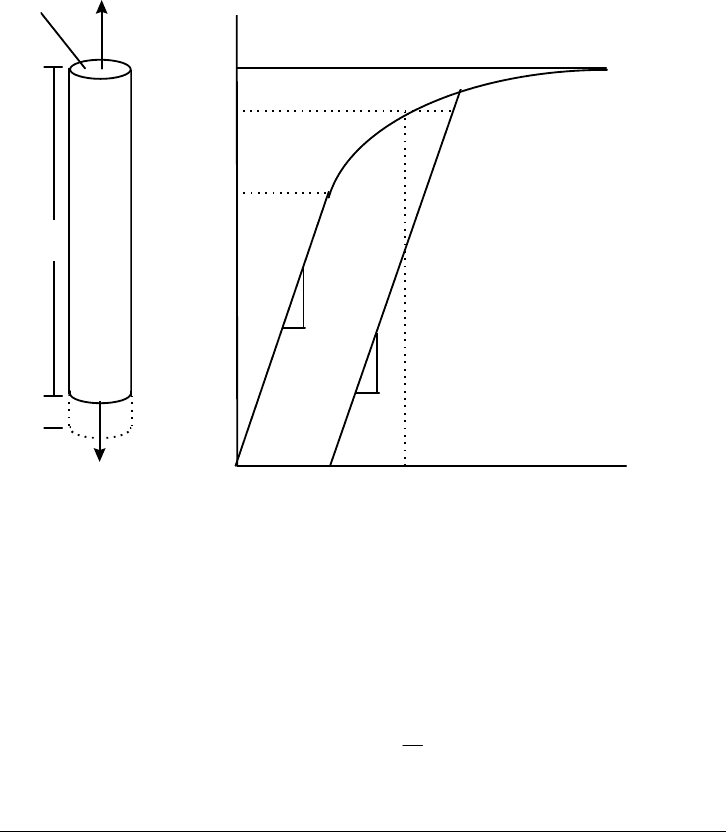
D.4.1 One-Dimensional Loading
Figure D-5 depicts the results of a uniaxial tension test on a sample of casing
steel. Dividing the applied force, F, by the cross-sectional area of the sample, A,
the axial stress can be determined. Similarly, the axial strain
ε
=
∆
LL/ can also
be directly measured. The right-hand portion of Figure D-5 is a plot of stress as a
function of strain. Notice from the figure that as the sample is loaded along path
OA, the relation between stress and strain is linear,
σ
ε
=
+
mb (D-37)
where m is the slope of the line and
b
is the value of
σ
at
ε
=
0. If the sample
were loaded to any point between O and A and then unloaded, the path OA
would, within practical limits, be retraced to the origin. Such behavior is termed
elastic. Evaluating the constants in equation (D-37),
b
=
0
and
m
E
=
so that:
σ
ε
=
E (D-38)
The constant E is called Young’s modulus.
σ
y
σ
API
σ
u
B
C
D
A
F
E
1
E
1
0
0.005
ε = ∆L / L
E
σ = F / A
∆L
L
A
F
G
Figure D-5. Typical Uniaxial Stress-Strain Curve
Before proceeding to higher loading states, it is worth mentioning that axial strain
is not the only dimensional change that will occur in the bar sample. Extension in
the axial dimension will be accompanied by contraction in the transverse
direction. This contraction in the transverse direction will also vary linearly with
the axial loading in the sense that:
σ
µ
µεε
E
transverse
−=−=
(D-39)
D-14 Casing/Tubing Design Manual
October 2005

where
µ
is Poisson’s ratio. Notice that
µ
can also be measured directly during
the deformation experiment. The quantities
µ
and
E
are independent and
completely determine isotropic linearly elastic stress-strain behavior for
isothermal loading.
Consider now an experiment where the sample is loaded along path OABC. The
following facts are pertinent:
• Above the stress state corresponding to point A, the relation between
stress and strain is no longer linear.
• Upon unloading from any point C above point A, the metal will not
retrace the original loading path, but rather will unload along path CDE
which is parallel to path OA. Unloading along path CDE occurs
elastically.
• After it is completely unloaded, the material will now possess a
permanent, inelastic strain (
ε
= OE).
• If the bar at state E is now reloaded, the stress-strain behavior will be
elastic and follow path EDC. Continued loading beyond the stress level
corresponding to point C will follow path CFG.
• Point G represents the ultimate strength of the material. States beyond
that corresponding to point G are undefined.
Behavior of the sample beyond point A is termed inelastic. Following the first
occasion for which the stress corresponding to point A is exceeded, it will be
necessary to compile a new set of constitutive (stress-strain) relations for the
material. Because of its importance as a limit point of elastic behavior
6
, the stress
corresponding to point A is given a special name, the initial yield stress, denoted
σ
y
. As will be emphasized later, the yield stress will change with inelastic
deformation. For example, recalling the comments of the previous paragraph,
after the material is loaded to point C on the stress-strain curve, point C becomes
the new yield stress. Loading/unloading along the line CDE is characterized by
elastic behavior. If subsequent loading goes beyond point C, the yield stress will
again change.
The description of material behavior beyond yield is much more complicated in
that now, stress-strain behavior depends not only on the current state, but also
on the previous history of loading. As an example, consider points B and D on
the uniaxial stress-strain curve. Both points correspond to the same value of
stress. However, it is obvious from the figure that a small increase in stress, ,
will produce different values of strain increment depending on whether the
current state actually corresponds to point B or to point D.
For loadings beyond the initial yield stress, two additional moduli are commonly
used to describe material behavior. The first modulus, called the tangent
modulus,
, is the instantaneous slope of the stress-strain curve,
E
t
6
For simplicity, the yield point, signifying the onset of inelastic behavior, and the
proportional limit, signifying the upper limit of applicability of equation (D-38) have
been assumed to coincide. However, for real materials, this is not always true.
Casing/Tubing Design Manual D-15
October 2005

E
d
d
t
≡
σ
ε
(D-40)
The second modulus, called the secant modulus,
is the slope of a line from the
origin to the point on the curve representing the current stress/strain state:
E
s
E
s
≡
σ
ε
(D-41)
Careful examination of Figure D-5 reveals that for all states of stress,
allfor
σ
ts
EEE ≥≥ (D-42)
and
EE Efor
st
=
y
=
≤
σ
σ
(D-43)
Clearly,
and are functions of both the current stress state and the entire
history of loading leading to the current stress state.
E
t
E
s
D.4.2 American Petroleum Institute (API)
Parameters
In the preceding section, the uniaxial stress-strain curve was discussed in
general terms common to the study of mechanics of materials. By convention,
special groups will introduce alternate definitions that are felt to better serve the
needs of a particular engineering community.
D.4.2.1 API Yield Stress
The yield stress,
σ
y
, is a difficult, if not impossible, number to obtain
experimentally. Close examination of the character of the curve in Figure D-5 will
indicate that, experimentally, by the time one detects inelastic behavior, the yield
stress has already been exceeded. In order to circumvent this experimental
problem, it is common practice to approximate the yield stress by means of a
suitable alternate definition.
For example, probably the most popular alternate definition of yield stress is the
so-called 0.2% offset stress which is determined by the intersection of the
experimental stress-strain curve with a line parallel to the elastic portion of the
curve (i.e., slope =
E
) and passing through the point = 0, = 0.002 (such a
line would be similar to line CDE in Figure D-5). On the other hand, the API
defines the yield stress as the stress corresponding to
ε
= 0.005
7
. As indicated in
Figure D-5,
σ
API
, the API yield stress, does not in general correspond to
σ
y
.
7
The value of strain corresponding to yield may vary with grade. For example, the yield
stress for grade P-110 is defined as the stress corresponding to
ε
= 0.006, and the yield
stress for grade Q-125 is defined as the stress corresponding to
ε
= 0.0065.
D-16 Casing/Tubing Design Manual
October 2005

D.4.2.2 Ultimate Stress and Elongation
The ultimate stress,
σ
u
, is the maximum stress recorded at the time the
specimen breaks. Corresponding to this stress will be a given value of strain. The
value of this ultimate strain, or elongation, is a measure of the ductility of the
steel.
The two stress-strain pairs (
σ
API
, 0.005) and (
σ
u
, Elongation) are the only
points taken from the uniaxial stress-strain curve for use in API formulas. Table
D-1 presents a list of the minimum acceptable values of
σ
API
and
σ
u
for tubular
steel grades currently recognized by the API.
Table D-1. API Minimum Tensile Requirements
Minimum Yield Minimum Ultimate
Grade Metric
(MPa)
English
(ksi)
Metric
(MPa)
English
(ksi)
H-40 276 40 414 60
J-55 379 55 517 75
K-55 379 55 655 95
N-80 552 80 689 100
L-80 552 80 655 95
C-90 621 90 689 100
T-95 655 95 724 105
P-110 758 110 862 125
Q-125 862 125 931 135
D.4.3 Needleman’s Model
The stress-strain curve illustrated in Figure D-5 is typical of oil field steels and it
is sometimes useful to have an equation to describe such a curve. The
advantages of such an equation are:
• Elimination of the need to interpolate between experimental data points,
because the equation will explicitly define a stress corresponding to any
given strain.
• The ability to perform parameter studies to determine the effects of
various stress-strain parameters on tubular performance.
Casing/Tubing Design Manual D-17
October 2005
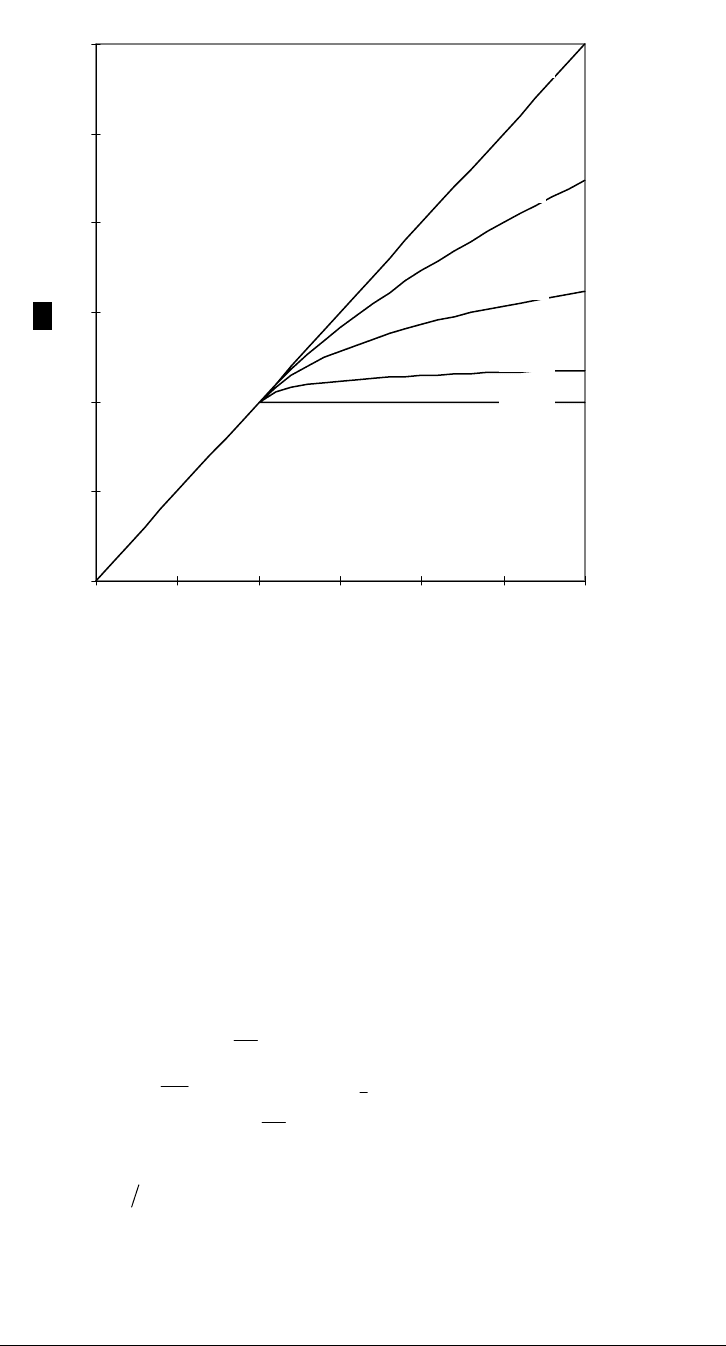
0
0.5
1
1.5
2
2.5
3
00.511.522.53
ε/ε
y
y
n = 2
n = 1
n = 5
n = 20
n =
ϑ
Figure D-6. Behavior of Needleman's Model for Various Values of Work-Hardening
Parameter
Of course, below the yield stress, the stress-strain curve is linear and described
completely by equation (D-38). The problem arises in attempting to describe the
nonlinear or inelastic portion of the curve.
A variety of equations or models have been proposed in the literature for
describing, or fitting, the stress-strain curve generated by a uniaxial test. It is
beyond the scope of this discussion to detail these various proposals. Rather,
here only the model proposed by Needleman [1975] will be discussed.
Needleman’s model may be expressed in equation form as:
σ
σ
ε
ε
εε
ε
ε
εε
y
y
y
y
n
y
for
nnfor
=
≤
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
+−
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
≥
⎧
⎨
⎪
⎪
⎪
⎩
⎪
⎪
⎪
1
1
, (D-44)
where
ε
σ
yy
E=
is the strain corresponding to yield and is the work-
hardening parameter which determines the shape of the stress-strain curve
beyond yield. Needleman’s model is continuous and has a continuous derivative
at
n
ε
ε
=
y
for all finite values of . n
D-18 Casing/Tubing Design Manual
October 2005

Figure D-6 is a plot of
σ
σ
y
versus
ε
ε
y
for various values of . Notice that
. If we associate work hardening with the amount of work (area under
the curve) necessary to increase the strain after the yield stress has been
exceeded, then an increase in the value of
corresponds to a decrease in the
work hardening character of the stress-strain curve beyond yield
n
1<<∞n
n
8
.
Table D-2 lists values of
σ
y
and n that correspond to the minimum yield and
ultimate properties of API tubular steels for casing. Figure D-7 presents this
same information graphically. Notice that for each grade the proportional limit or
yield stress, denoted in this text as
σ
y
, and the API yield stress,
σ
API
, differ by
approximately 70 to 105 MPa (10,000-15,000 psi). This discrepancy is due to the
arbitrary definition of
σ
API
, and is an important fact to keep in mind when the
structural limits of certain aspects of tubular behavior are defined in terms of the
onset of yield.
Table D-2. Needleman Parameters for API Grades
Yield Stress
Grade Metric
(MPa)
English
(psi)
n
H-40 187 27,100 9.8
J-55 287 41,600 12.6
K-55 235 34,100 6.6
L-80 477 69,200 23.0
N-80 461 66,900 17.5
C-90 567 82,300 39.1
T-95 603 87,400 41.0
P-110 678 98,400 28.8
Q-125 800 116,100 47.5
8
To be entirely correct, work hardening refers to the amount of permanent,
unrecoverable work associated with an increase in applied stress. However, even with
this definition,
is inversely proportional to the work hardening character of the
material being modeled.
n
Casing/Tubing Design Manual D-19
October 2005
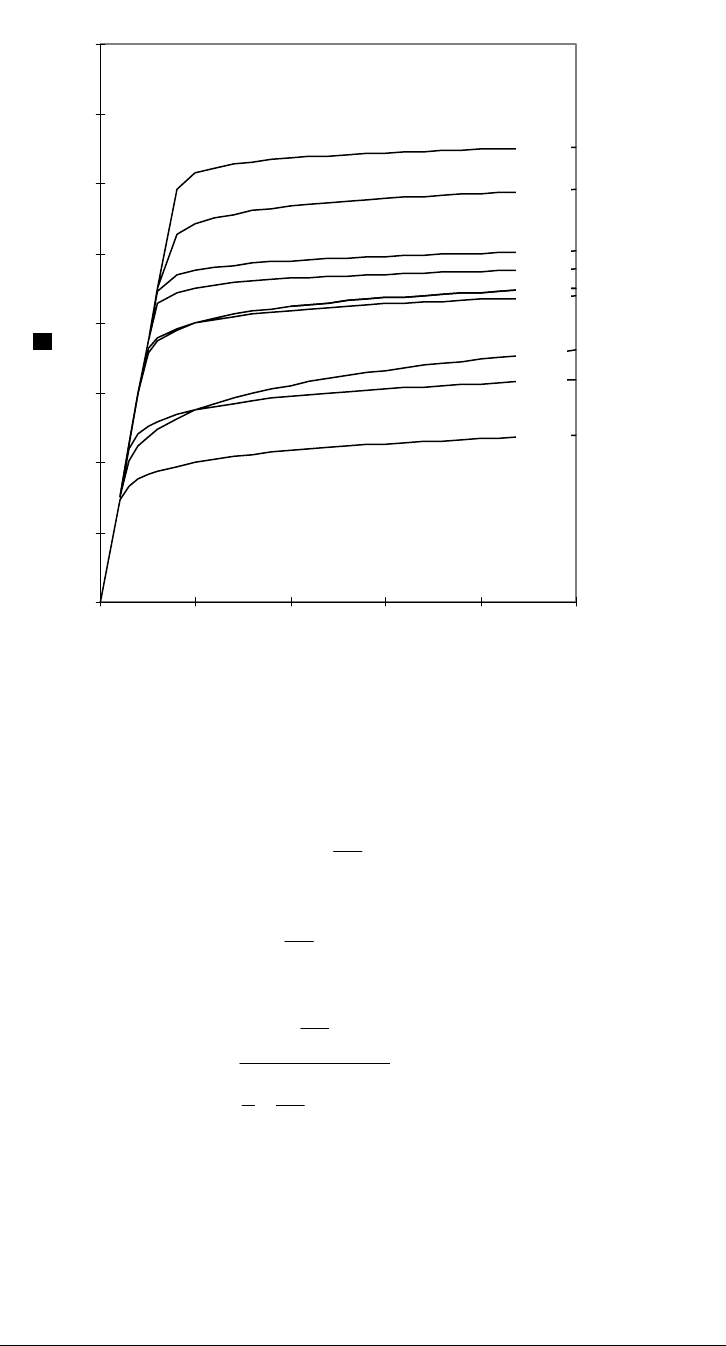
0
20
40
60
80
100
120
140
160
0 0.005 0.01 0.015 0.02 0.025
ε
(ksi)
H-40
K-55
T-95
P-110
Q-125
C-90
L-80
J-55
N-80
Figure D-7. Stress-Strain Curves for API Steels using Needleman's Model
Manipulation of equation (D-44) yields the following expressions for parameters
previously introduced in terms of Needleman’s model:
EE E for
ts
y
y
y
=== ≤
σ
ε
εε
(D-45)
EE for
t
y
n
y
=
⎛
⎝
⎜
⎞
⎠
⎟
≥
−
σ
σ
εε
1
(D-46)
EE
n
for
s
y
y
n
y
=
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
+
≥
σ
σ
σ
σ
εε
1
11
(D-47)
D.4.4 Ideal Plastic Behavior (Perfect Plasticity)
The stress-strain curve in Figure D-5 satisfactorily models the most general type
of uniaxial behavior that will be considered in this text. It happens that a number
of tubular steels exhibit stress-strain behavior that, within the limits of strain
D-20 Casing/Tubing Design Manual
October 2005

necessary to solve the majority of practical problems, possess a zero slope
beyond yield. Such behavior is termed ideally or perfectly plastic.
Recall Figure D-6 and notice that in the limit as the value of the work-hardening
parameter n becomes infinite, we may model ideal plastic behavior. In particular,
from equation (D-44),
lim lim
limexp ln
n
y
n
y
n
n
y
nn
n
nn
→∞ →∞
→∞
=
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
+−
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
=
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
+−
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
⎧
⎨
⎪
⎩
⎪
⎫
⎬
⎪
⎭
⎪
σ
σ
ε
ε
ε
ε
1
1
1
1
(D-48)
The limit of the expression in braces can be evaluated using l’Hospital’s rule,
lim ln
n
y
n
nn
→∞
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
+−
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
=
1
1
ε
ε
0
(D-49)
which, upon substitution into equation (D-48), leads to:
lim
n
y
→∞
=
σ
σ
1.(D-50)
and, from equations (D-40) and (D-41),
Eforn
ty
=
≥→
∞
0
ε
ε
,
(D-51)
Eforn
s
y
y
=≥
σ
ε
εε
, →∞
(D-52)
Notice that for
n
the inverse relation
→∞
(
)
εεσ
=
is no longer single valued.
That is, given
σ
σ
=
y
it is not possible to determine a unique value of strain. At
first glance, it would appear that the uncertainties associated with a multi-valued
strain-stress relation would render the limiting case
n →
∞
a circumstance to be
avoided. However in many problems of practical interest, useful solutions can be
obtained from ideal plastic behavior [Prager and Hodge, 1951]. In such
instances, inconveniences associated with the uncertainty of the stress-strain
relation are outweighed by the simplicity of the description of the plastic stress
state. Further, as might be anticipated from Figure D-6, ideal plastic behavior is
also useful for providing a lower bound or conservative estimate of the load
response of a particular steel grade inasmuch as all beneficial effects of work
hardening are ignored.
D.5 Multi-Dimensional Loading
During actual field application, any point in a tubular string will be subjected to
multiple stresses rather than the simple uniaxial stress state discussed above. As
was the case in the introductory discussion, the response of the casing steel can
be divided into an elastic response and an inelastic response, the demarcation
Casing/Tubing Design Manual D-21
October 2005
