Coburn J.W., Herdlick J.D. College Algebra: Graphs and Models
Подождите немного. Документ загружается.


730 CHAPTER 8 Analytic Geometry and the Conic Sections 8–24
College Algebra G&M—
REINFORCING BASIC CONCEPTS
More on Completing the Square
From our work so far in Chapter 8, we realize the process of completing the square has much greater use than simply as a tool
for working with quadratic equations. It is a valuable tool in the application of the conic sections, as well as other areas. The
purpose of this Reinforcing Basic Concepts is to strengthen the ability and confidence needed to apply the process correctly.
This is important because in some cases the values of a and b are rational or irrational numbers. No matter what the context,
1. The process begins with a coefficient of 1. For we recognize the
equation of an ellipse, since the coefficients of the squared terms are positive and unequal. To study or graph this
ellipse, we’ll use the standard form to identify the values of a, b, and c. Grouping the like-variable terms gives
and to complete the square, we factor out the lead coefficient of each group (to get a coefficient of 1):
Subtracting 192 from both sides brings us to the fundamental step for completing the square.
2. The quantity will complete a trinomial square. For this example we obtain
for x, and for y, with these numbers inserted in the appropriate group:
complete the square
Due to the distributive property, we have in effect added and (for a total of 207) to the left
side of the equation:
adds adds
to left side to left side
This brings us to the final step.
3. Keep the equation in balance. Since the left side was increased by 207, we also increase the right side by 207.
adds adds add
to left side to left side to right side
The quantities in parentheses factor, giving We then divide by 15 and simplify, obtaining
the standard form Note the coefficient of each binomial square is not 1, even after setting
the equation equal to 1. In the Strengthening Core Skills feature of this chapter, we’ll look at how to write equations of
this type in standard form to obtain the values of a and b. For now, practice completing the square using these exercises.
Exercise 1:
Exercise 2: 28x
2
56x 48y
2
192y 195 0
100x
2
400x 18y
2
108y 554 0
41x 32
2
3
91y 12
2
5
1.
201x 32
2
271y 12
2
15.
180 27 20727
#
1 2720
#
9 180
201x
2
6x 92 271y
2
2y 12192 207
27
#
1 2720
#
9 180
201x
2
6x 92 271y
2
2y 12192
27
#
1 2720
#
9 180
201x
2
6x 92 271y
2
2y 12192
a
1
2
#
2b
2
1a
1
2
#
6b
2
9
a
1
2
#
linear cofficientb
2
201x
2
6x
2 271y
2
2y
2 192 0
120x
2
120x
2 127y
2
54y
2 192 0
20x
2
120x 27y
2
54y 192 0,
8. Find the equation of each relation and state its
domain and range.
a. b.
9. Find the equation of the ellipse having foci at
(0, 13) and , with a minor axis of length
10 units.
10. Find the equation of the ellipse (in standard form)
if the vertices are ( ) and (4, 0) and the
distance between the foci is units.413
4, 0
10, 132
2
2
4
6
8
10
4
6
8
10
y
(3, 6)
(7, 2)
(3, 2)
(1, 2)
864210864210
x
5432154321
1
2
3
4
5
2
3
4
1
5
y
x
(3, 5)
(3, 3)
(5, 1) (1, 1)
cob19545_ch08_716-730.qxd 10/25/10 2:45 PM Page 730
8–25 731
College Algebra G&M—
8.3 The Hyperbola
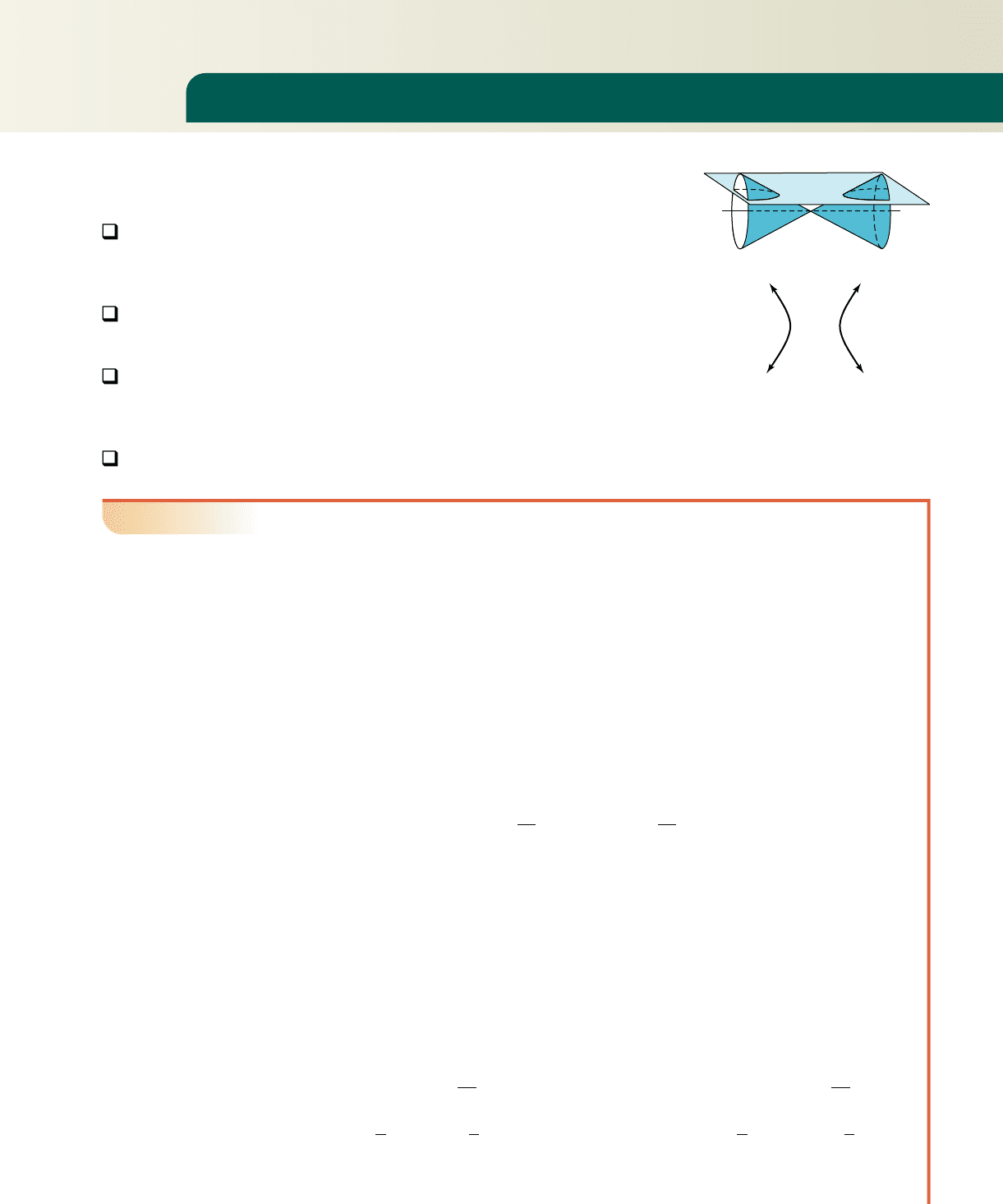
As seen in Section 8.1 (see Figure 8.24), a hyperbola
is a conic section formed by a plane that cuts both
nappes of a right circular cone. A hyperbola has two
symmetric parts called branches, which open in
opposite directions. Although the branches appear
to resemble parabolas, we will soon discover they
are actually a very different curve.
A. The Equation of a Hyperbola
In Section 8.2, we noted that for the equation
if the equation is that of a circle, if the equa-
tion represents an ellipse. Both cases contain a sum of second-degree terms. Perhaps
driven by curiosity, we might wonder what happens if the equation has a difference of
second-degree terms. Consider the equation It appears the graph
will be centered at (0, 0) since no shifts are applied (h and k are both zero). Using the in-
tercept method to graph this equation reveals an entirely new curve, called a hyperbola.
EXAMPLE 1
䊳
Graphing a Central Hyperbola
Graph the equation using intercepts and additional points
as needed.
Solution
䊳
given
substitute 0 for
x
simplify
divide by
Since y
2
can never be negative, we conclude that the graph has no y-intercepts.
Substituting to find the x-intercepts gives
given
substitute 0 for
y
simplify
divide by 9
square root property
and simplify
(4, 0) and
x
-intercepts
Knowing the graph has no y-intercepts, we select inputs greater than 4 and less
than to help sketch the graph. Using and yields
given
substitute for
x
simplify
subtract 225
divide by
square root property
decimal form
ordered pairs
15, 2.252
15, 2.25215, 2.252
15, 2.252
y 2.25
y 2.25 y 2.25
y 2.25
y
9
4
y
9
4
y
9
4
y
9
4
y
2
81
16
16 y
2
81
16
16y
2
81 16y
2
81
225 16y
2
144
225 16y
2
144
9 1252 16y
2
1445
2
152
2
25 9 1252 16y
2
144
9 152
2
16y
2
144
9 152
2
16y
2
144
9 x
2
16y
2
144
9 x
2
16y
2
144
x 5x 54
14, 02
x 4x 4
x 116
and
x 116
x
2
16
9 x
2
144
9 x
2
16102
2
144
9 x
2
16y
2
144
y 0
16 y
2
9
16y
2
144
9 102
2
16y
2
144
9 x
2
16y
2
144
9x
2
16y
2
144
9x
2
16y
2
144.
A B,A B,
Ax
2
By
2
F,
LEARNING OBJECTIVES
In Section 8.3 you will see
how we can:
A. Use the equation of a
hyperbola to graph
central and noncentral
hyperbolas
B. Distinguish between the
equations of circles,
ellipses, and hyperbolas
C. Locate the foci of a
hyperbola and use the
foci and other features to
write its equation
D. Solve applications
involving foci
Hyperbola
Axis
Figure 8.24
cob19545_ch08_731-745.qxd 10/25/10 2:50 PM Page 731

College Algebra G&M—
Plotting these points and connecting them
with a smooth curve, while knowing there are no
y-intercepts, produces the graph in the figure.
The point at the origin (in blue) is not a part of
the graph, and is given only to indicate the
“center” of the hyperbola. The points
and (4, 0) are called vertices, and the center
of the hyperbola is always the point halfway
between them.
Now try Exercises 7 through 22
䊳
As with the circle and ellipse, the hyperbola fails the vertical line test and we must
graph the relation on a calculator by writing its equation in two parts, each of which is
a function. For the hyperbola in Example 1, this gives
original equation
isolate
y
-term
multiply by 1
divide by 16
take square roots
The graph is shown in Figure 8.25.
Since the hyperbola in Example 1 crosses a horizontal line of symmetry, it is
referred to as a horizontal hyperbola. If the center is at the origin, we have a central
hyperbola. The line passing through the center and both vertices is called the trans-
verse axis (vertices are always on the transverse axis), and the line passing through the
center and perpendicular to this axis is called the conjugate axis (see Figure 8.26).
In Example 1, the coefficient of x
2
was positive and we were subtracting 16y
2
:
. The result was a horizontal hyperbola. If the y
2
-term is positive
and we subtract the term containing x
2
, the result is a vertical hyperbola (Figure 8.27).
x
y
Transverse axis
Conjugate
axis
Vertex
Vertex
Center
Vertical
hyperbola
x
y
Conjugate
axis
Transverse
axis
Horizontal
hyperbola
VertexVertex
Center
Figure 8.27
Figure 8.26
9x
2
16y
2
144
Y
1
B
9X
2
144
16
,
Y
2
B
9X
2
144
16
y
B
9x
2
144
16
y
2
9x
2
144
16
16y
2
9x
2
144
16y
2
144 9x
2
9 x
2
16y
2
144
14, 02
x
y
(0, 0)
(5, 2.25)
(5, 2.25)
(5, 2.25) (5, 2.25)
(4, 0) (4, 0)
Hyperbola
9.4 9.4
6.2
6.2
Figure 8.25
732 CHAPTER 8 Analytic Geometry and the Conic Sections 8–26
cob19545_ch08_731-745.qxd 10/25/10 2:50 PM Page 732
EXAMPLE 2
䊳
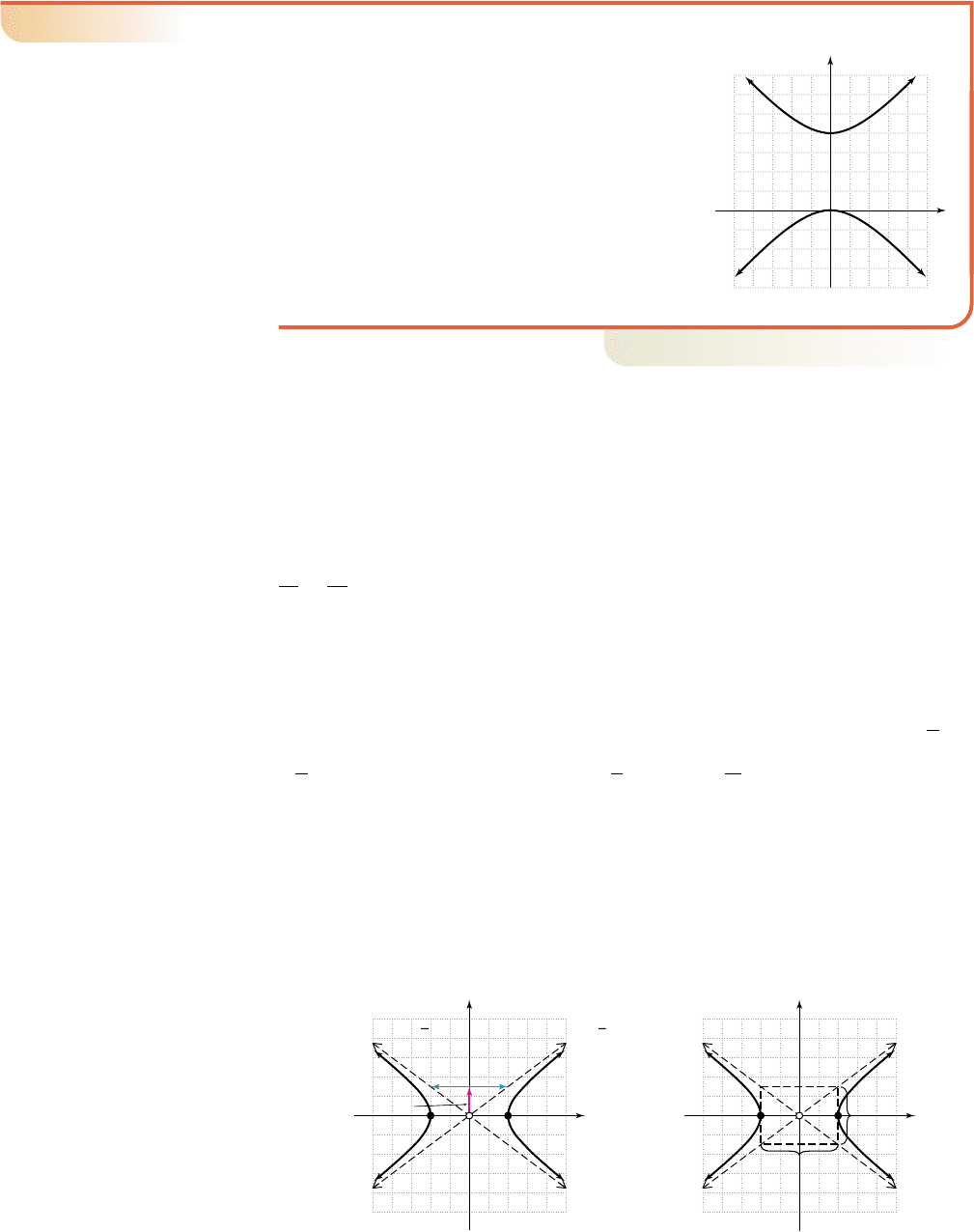
Identifying the Axes, Vertices, and Center of a Hyperbola from Its Graph
For the hyperbola shown, state the location of the
vertices and the equation of the transverse axis.
Then identify the location of the center and the
equation of the conjugate axis.
Solution
䊳
By inspection we locate the vertices at (0, 0) and
(0, 4). The equation of the transverse axis is
The center is halfway between the vertices
at (0, 2), meaning the equation of the conjugate
axis is
Now try Exercises 23 through 26
䊳
Standard Form
As with the ellipse, the polynomial form of the equation is helpful for identifying
hyperbolas, but not very helpful when it comes to graphing a hyperbola (since we still
must go through the laborious process of finding additional points). For graphing, stan-
dard form is once again preferred. Consider the hyperbola from
Example 1. To write the equation in standard form, we divide by 144 and obtain
. By comparing the standard form to the graph, we note represents
the distance from center to vertices, similar to the way we used a previously. But
since the graph has no y-intercepts, what could represent? The answer lies in
the fact that branches of a hyperbola are asymptotic, meaning they will approach
and become very close to imaginary lines that can be used to sketch the graph. For
a central hyperbola, the slopes of the asymptotic lines are given by the ratios and
with the related equations being and The graph from Example 1
is repeated in Figure 8.28, with the asymptotes drawn. For a clearer understanding of
how the equations for the asymptotes were determined, see Exercise 87.
A second method of drawing the asymptotes involves drawing a central rectangle
with dimensions 2a by 2b, as shown in Figure 8.29. The asymptotes will be the ex-
tended diagonals of this rectangle. This brings us to the equation of a hyperbola in
standard form.
Central rectangle methodSlope method
x
y
(4, 0)
2b
2a
x
y
(0, 0)
(4, 0)
(4, 0)
rise
b 3
Slope m
3
4
3
4
Slope m
run
a 4
Figure 8.29
Figure 8.28
y
b
a
x.y
b
a
x
b
a
,
b
a
b 3
a 4
x
2
4
2
y
2
3
2
1
9x
2
16y
2
144
y 2.
x 0.
x
55
4
5
y
College Algebra G&M—
8–27 Section 8.3 The Hyperbola 733
cob19545_ch08_731-745.qxd 10/25/10 2:50 PM Page 733
The Equation of a Hyperbola in Standard Form
The equation The equation
represents a horizontal hyperbola represents a vertical hyperbola
with center (h, k) with center (h, k)
• transverse axis • transverse axis
• conjugate axis • conjugate axis
• gives the distance from • gives the distance from
center to vertices. center to vertices.
• Asymptotes can be drawn by starting at (h, k) and using slopes
EXAMPLE 3
䊳
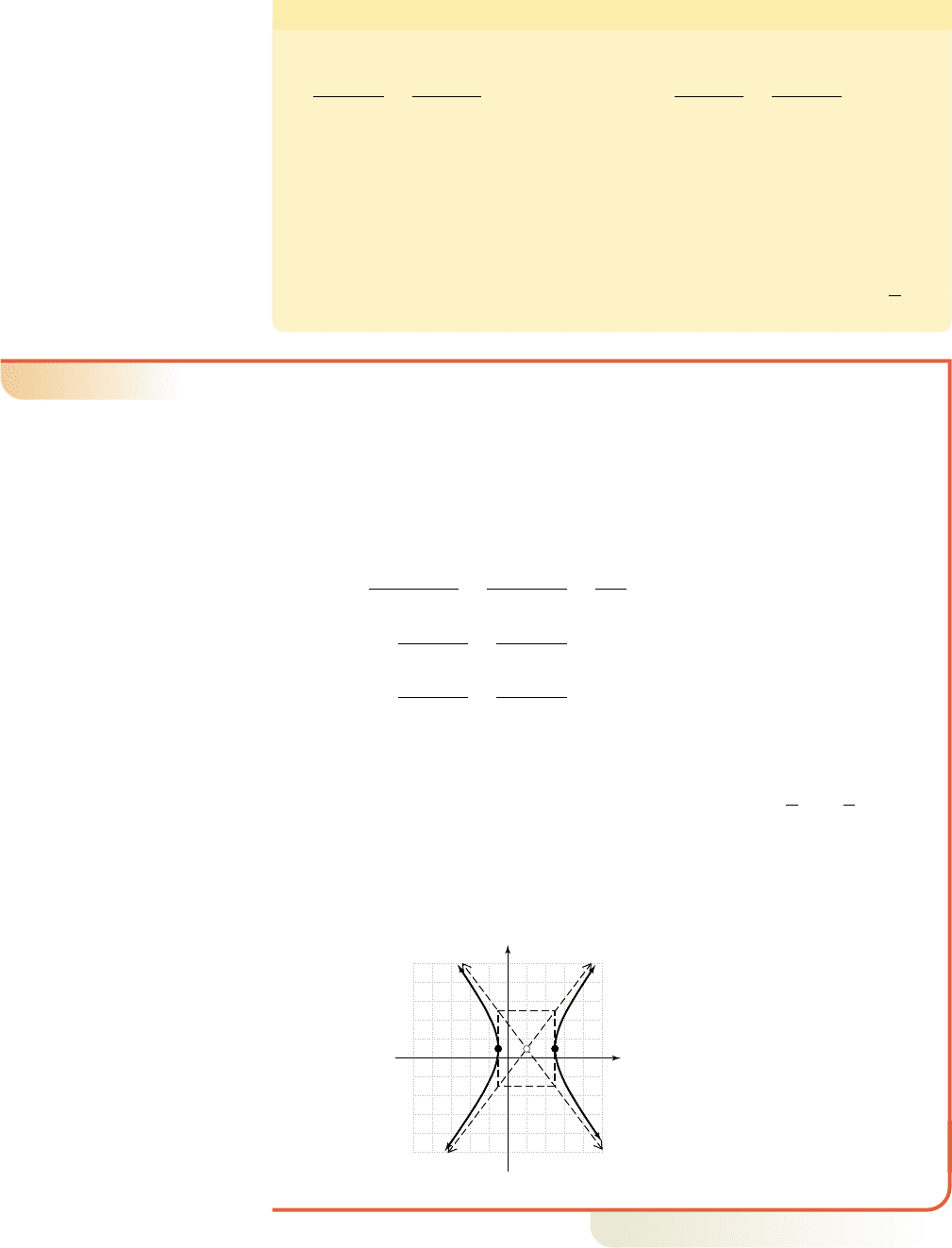
Graphing a Hyperbola Using Its Equation in Standard Form
Sketch the graph of , and label the center, vertices,
and asymptotes.
Solution
䊳
Begin by noting a difference of the second-degree terms, with the x
2
-term
occurring first. This means we’ll be graphing a horizontal hyperbola whose center
is at (2, 1). Continue by writing the equation in standard form.
given equation
divide by 144
simplify
write denominators in squared form
Since the vertices are a horizontal distance of 3 units from the center (2, 1),
giving and . After plotting the center and
vertices, we can begin at the center and count off slopes of or
draw a rectangle centered at (2, 1) with dimensions (horizontal dimension)
by (vertical dimension) to sketch the asymptotes. The complete graph is
shown here.
Now try Exercises 27 through 44
䊳
x
y
(2, 1)
(5, 1)(1, 1)
m d
m d
Horizontal hyperbola
Center at (2, 1)
Vertices at (1, 1) and (5, 1)
Transverse axis: y 1
Conjugate axis: x 2
Width of rectangle
horizontal dimension and
distance between vertices
2a 2(3) 6
Length of rectangle
(vertical dimension)
2b 2(4) 8
冢冣
2142 8
2132 6
m
b
a
4
3
,
12 3, 12S 11, 1212 3, 12S 15, 12
a 3
1x 22
2
3
2
1y 12
2
4
2
1
1x 22
2
9
1y 12
2
16
1
161x 22
2
144
91y 12
2
144
144
144
161x 22
2
91y 12
2
144
161x 22
2
91y 12
2
144
m
b
a
.
冟
b
冟冟
a
冟
y kx h
x hy k
1y k2
2
b
2
1x h2
2
a
2
1
1x h2
2
a
2
1y k2
2
b
2
1
College Algebra G&M—
734 CHAPTER 8 Analytic Geometry and the Conic Sections 8–28
cob19545_ch08_731-745.qxd 10/25/10 2:50 PM Page 734

If the hyperbola in Example 3 were a central hyperbola, the equations of the
asymptotes would be and . But the center of this graph has been
shifted 2 units right and 1 unit up. Using our knowledge of shifts and translations, the
equations for the asymptotes of the shifted hyperbola must be
1. , or in simplified form, and
2. or .
Using , and
(obtained by solving for y in the original equation), a calculator generated graph of the
hyperbola and its asymptotes is shown here (Figures 8.30 and 8.31).
Polynomial Form
If the equation is given as a polynomial in expanded form, complete the square in x and
y, then write the equation in standard form.
EXAMPLE 4
䊳
Graphing a Hyperbola by Completing the Square
Graph the equation by completing the square. Label the center
and vertices and sketch the asymptotes. Then graph the hyperbola on a graphing calculator and
use the feature with a “friendly” window to locate four additional points whose coordinates
are rational.
Solution
䊳
Since the y
2
-term occurs first, we assume the equation represents a vertical hyperbola, but wait for
the factored form to be sure (see Exercise 91).
given
collect like-variable terms; subtract 68
factor out 9 from
y
-terms and from
x
-terms
complete the square
adds adds
add to right
factor vertical hyperbola
divide by 9 (standard form)
write denominators in squared form
1y 32
2
1
2
1x 22
2
3
2
1
1y 32
2
1
1x 22
2
9
1
S 9 1y 32
2
11x 22
2
9
81 14 2
1
14 2 49 19 2 81
91y
2
6y 92 11x
2
4x 42 68 81 142
1 9 1y
2
6y
___
2 11x
2
4x
___
268
9 y
2
54y x
2
4x 68
9 y
2
x
2
54y 4x 68 0
TRACE
9y
2
x
2
54y 4x 68 0
7.4 11.4
8.3
10.3
Figure 8.31
Y
2
B
161X 22
2
144
9
1Y
1
B
161X 22
2
144
9
1
y
4
3
x
11
3
1y 12
4
3
1x 22
y
4
3
x
5
3
1y 12
4
3
1x 22
y
4
3
xy
4
3
x
College Algebra G&M—
c
c
cc
8–29 Section 8.3 The Hyperbola 735
Figure 8.30
cob19545_ch08_731-745.qxd 10/25/10 2:51 PM Page 735

The center of the hyperbola is with and a transverse axis of . The
vertices are at and and . After plotting the center and
vertices, we draw a rectangle centered at with a horizontal “width” of and a
vertical “length” of to sketch the asymptotes. The completed graph is given in Figure 8.32.
To graph the hyperbola on a calculator, we again solve for y.
factored form
isolate term containing
y
divide by 9
take square roots
subtract 3
Using the friendly window shown, we can use the arrow
keys to though x-values and find the points
and on the upper branch, with
and on the lower branch. Note
how these points show that a hyperbola is symmetric to
its center, as well as the horizontal line and vertical line
through its center. The graph is shown in Figure 8.33.
Now try Exercises 45 through 48
䊳
B. Distinguishing between the Equations
of Circles, Ellipses, and Hyperbolas
So far we’ve explored numerous graphs of circles, ellipses, and hyperbolas. In Exam-
ple 5 we’ll attempt to identify a given conic section from its equation alone (without
graphing the equation). As you’ve seen, the corresponding equations have unique char-
acteristics that can help distinguish one from the other.
19.2, 5.6215.2, 5.62
19.2, 0.4215.2, 0.42
TRACE
Y
1
B
9 1X 22
2
9
3, Y
2
B
9 1X 22
2
9
3
y
B
9 1x 22
2
9
3
y 3
B
9 1x 22
2
9
1y 32
2
9 1x 22
2
9
9 1y 32
2
9 1x 22
2
9 1y 32
2
1x 22
2
9
x
y
(2, 4)
(2, 3)
center
(2, 2)
m
m
Vertical hyperbola
Center at (2, 3)
Vertices at (2, 2) and (2, 4)
Transverse axis: x 2
Conjugate axis: y 3
Width of rectangle
(horizontal dimension)
2a 2(3) 6
Length of rectangle
vertical dimension and
distance between vertices
2b 2(1) 2
冢冣
1
3
1
3
2112 2
2132 612, 32
12, 4212, 3 12S 12, 2212, 3 12
x 2a 3, b 1,12, 32
College Algebra G&M—
7.4 11.4
9.2
3.2
Figure 8.33
A. You’ve just seen how
we can use the equation of a
hyperbola to graph central and
noncentral hyperbolas
736 CHAPTER 8 Analytic Geometry and the Conic Sections 8–30
Figure 8.32
cob19545_ch08_731-745.qxd 10/25/10 2:51 PM Page 736

College Algebra G&M—
EXAMPLE 5
䊳
Identifying a Conic Section from Its Equation
Identify each equation as that of a circle, ellipse, or hyperbola. Justify your choice
and name the center, but do not draw the graphs.
a. b.
c. d.
e. f.
Solution
䊳
a. Writing the equation as Since the
equation contains a difference of second-degree terms, it is the equation of a
(vertical) hyperbola (A and B have opposite signs). The center is at (0, 0).
b. Rewriting the equation as and dividing by 4 gives
The equation represents a circle of radius 2 , with the
center at (0, 0).
c. Writing the equation as we note a sum of second-degree
terms with unequal coefficients. The equation is that of an ellipse ,
with the center at (0, 0).
d. Rewriting the equation as we note the equation contains a
difference of second-degree terms. The equation represents a central
(horizontal) hyperbola (A and B have opposite signs), whose center is at (0, 0).
e. The equation is in factored form and contains a sum of second-degree terms
with unequal coefficients. This is the equation of an ellipse with the
center at .
f. Rewriting the equation as we note a difference of
second-degree terms. The equation represents a horizontal hyperbola (A and B
have opposite signs) with center
Now try Exercises 49 through 60
䊳
C. The Foci of a Hyperbola
Like the ellipse, the foci of a hyperbola play an important part in their application. A
long distance radio navigation system (called LORAN for short), can be used to deter-
mine the location of ships and airplanes and is based on the characteristics of a hyper-
bola (see Exercises 85 and 86). Hyperbolic mirrors are also used in some telescopes,
and have the property that a beam of light directed at one focus will be reflected to the
second focus. To understand and appreciate these applications, we use the analytic def-
inition of a hyperbola:
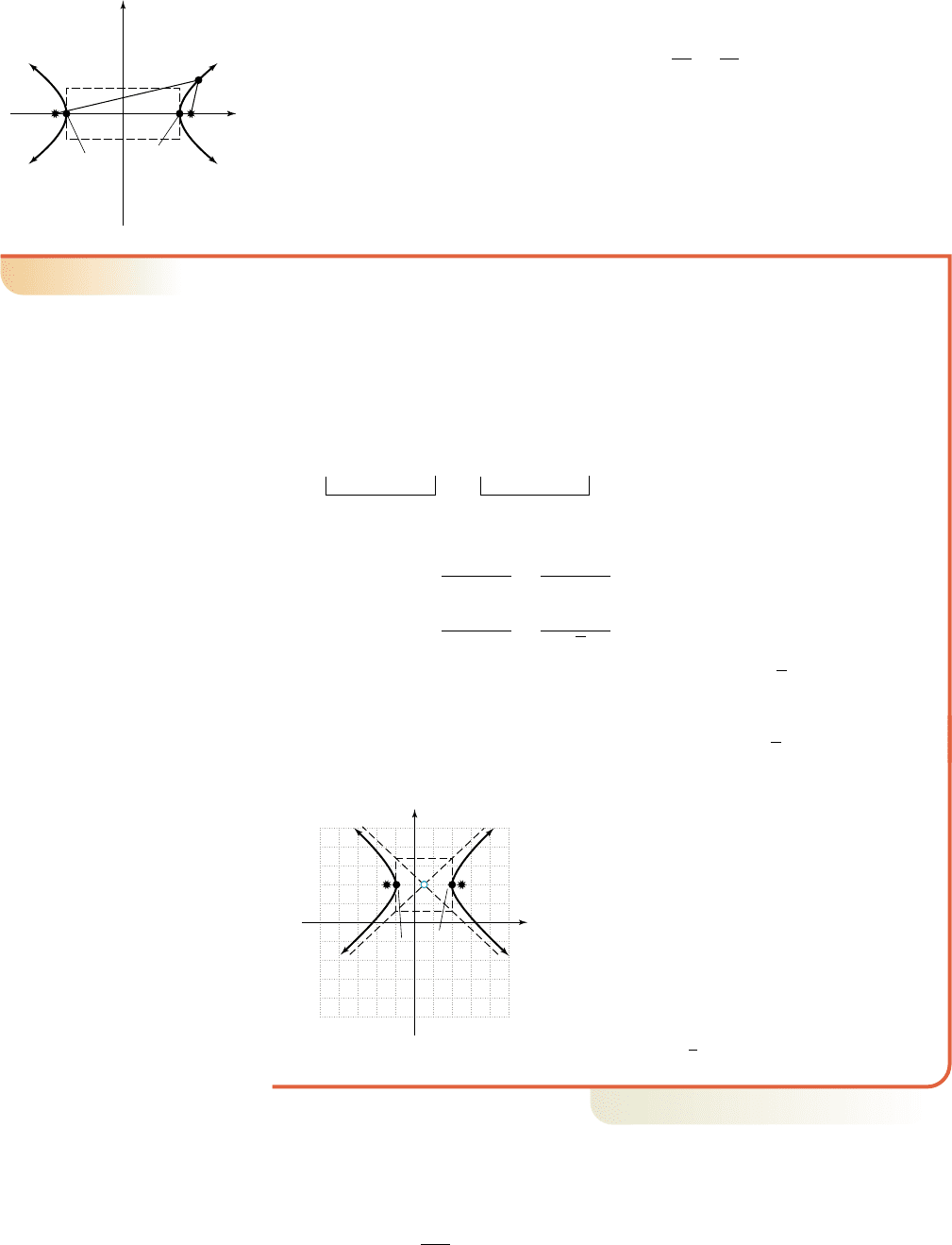
Definition of a Hyperbola
Given two fixed points f
1
and f
2
in a plane, a hyperbola
is the set of all points (x, y) such that the distance d
1
from f
1
to (x, y) and the distance d
2
from f
2
to (x, y),
satisfy the equation
In other words, the difference of these two distances
is a positive constant.
The fixed points f
1
and f
2
are called the foci of the
hyperbola, and all such points (x, y) are on the graph
of the hyperbola.
冟
d
1
d
2
冟
k.
y
x
|d
1
d
2
|
k
k > 0
d
2
d
1
f
1
f
2
(x, y)
15, 42.
41x 52
2
91y 42
2
36
12, 32
1A B2
25x
2
4y
2
100
1A B2
x
2
25y
2
225
1A B2x
2
y
2
4.
4x
2
4y
2
16
y
2
9x
2
36 shows h 0 and k 0.
41x 52
2
36 91y 42
2
31x 22
2
41y 32
2
12
25x
2
100 4y
2
x
2
225 25y
2
4x
2
16 4y
2
y
2
36 9x
2
B. You’ve just seen how
we can distinguish between
the equations of circles,
ellipses, and hyperbolas
8–31 Section 8.3 The Hyperbola 737
cob19545_ch08_731-745.qxd 10/25/10 2:51 PM Page 737
As with the analytic definition of the ellipse, it can be shown that the constant k is
again equal to 2a (for horizontal hyperbolas). To find the equation of a hyperbola in
terms of a and b, we use an approach similar to that of the ellipse (see Appendix V),
and the result is identical to that seen earlier: where
(see Figure 8.34).
We now have the ability to find the foci of any hyperbola—and can use this infor-
mation in many significant applications. Since the location of the foci play such an im-
portant role, it is best to remember the relationship as (called the foci
formula for hyperbolas), noting that for a hyperbola, and (also
and ). Be sure to note that for ellipses, the foci formula is since
(horizontal ellipses) or (vertical ellipses).
EXAMPLE 6
䊳
Graphing a Hyperbola and Identifying Its Foci by Completing the Square
For the hyperbola defined by find the
coordinates of the center, vertices, foci, and the dimensions of the central
rectangle. Then sketch the graph, including the asymptotes.
Solution
䊳
given
group terms; add 200
factor out leading coefficients
complete the square
adds adds
to right-hand side
factored form
divide by 63 and simplify
write denominators in squared form
1x ⫺ 12
2
3
2
⫺
1y ⫺ 42
2
1172
2
⫽ 1
1x ⫺ 12
2
9
⫺
1y ⫺ 42
2
7
⫽ 1
7 1x ⫺ 12
2
⫺ 91y ⫺ 42
2
⫽ 63
⫺9 116 2⫽ ⫺1447112⫽ 7
7 1x
2
⫺ 2x ⫹ 12⫺ 91y
2
⫺ 8y ⫹ 162⫽ 200 ⫹ 7 ⫹ 1⫺1442
7 1x
2
⫺ 2x ⫹
____
2⫺ 91y
2
⫺ 8y ⫹
____
2⫽ 200
7 x
2
⫺ 14x ⫺ 9y
2
⫹ 72y ⫽ 200
7 x
2
⫺ 9y
2
⫺ 14x ⫹ 72y ⫺ 200 ⫽ 0
7x
2
⫺ 9y
2
⫺ 14x ⫹ 72y ⫺ 200 ⫽ 0,
b 7 ca 7 c
c
2
⫽
冟
a
2
⫺ b
2
冟
c
2
7 b
2
c 7 bc
2
7 a
2
c 7 a
c
2
⫽ a
2
⫹ b
2
b
2
⫽ c
2
⫺ a
2
x
2
a
2
⫺
y
2
b
2
⫽ 1
College Algebra G&M—
(a, 0)
(⫺a, 0)
(⫺c, 0)
(c, 0)
y
(x, y)
x
Figure 8.34
cccc
S add 7 ⫹ 1⫺1442
738 CHAPTER 8 Analytic Geometry and the Conic Sections 8–32
This is a horizontal hyperbola with and
The center is at (1, 4), with vertices and (4, 4). Using the foci formula
yields showing the foci are and (5, 4)
(4 units from center). The central rectangle is
Drawing the rectangle and sketching the asymptotes results in the graph shown.
Now try Exercises 61 through 70
䊳
The focal chord for a horizontal hyperbola is a vertical line segment through the
focus with endpoints on the hyperbola. Similar to the focal chord of an ellipse, we can
use its length to find additional points on the graph of the hyperbola. The total length
is once again (for a horizontal hyperbola), meaning the distance from the foci L ⫽
2b
2
a
x
y
⫺10
10
⫺10 10
(1, 4)
(⫺2, 4)
(⫺3, 4)
(4, 4)
(5, 4)
冢冣
Horizontal hyperbola
Center at (1, 4)
Vertices at (⫺2, 4) and (4, 4)
Transverse axis: y ⫽ 4
Conjugate axis: x ⫽ 1
Location of foci: (⫺3, 4) and (5, 4)
Width of rectangle
horizontal dimension and
distance between vertices
2a ⫽ 2(3) ⫽ 6
Length of rectangle
(vertical dimension)
2b ⫽ 2(√7) ≈ 5.29
2132⫽ 6 by 217 ⬇ 5.29.
1⫺3, 42c
2
⫽ 9 ⫹ 7 ⫽ 16,c
2
⫽ a
2
⫹ b
2
1⫺2, 42
b ⫽ 17
1b
2
⫽ 72.1a
2
⫽ 92a ⫽ 3
cob19545_ch08_731-745.qxd 12/16/10 8:42 AM Page 738

to the graph (along the focal chord) is .
For Example 6, and , so the
vertical distance from focus to graph (in either
direction) is From the left focus
, we can now graph the additional
points , and
. From the right
focus (5, 4), we obtain (5, ) and (5, ).
Graphical verification is provided in Figure 8.35.
Also see Exercise 80.
As with the ellipse, if any two of the values for a, b, and c are known, the relation-
ship between them can be used to construct the equation of the hyperbola. See Exer-
cises 71 through 78.
D. Applications Involving Foci
Applications involving the foci of a conic section can take many forms. As before, only
partial information about the hyperbola may be available, and we’ll determine a solu-
tion by manipulating a given equation or constructing an equation from given facts.
EXAMPLE 7
䊳
Applying the Properties of a Hyperbola—The Path of a Comet
Comets with a high velocity cannot be
captured by the Sun’s gravity, and are slung
around the Sun in a hyperbolic path with the
Sun at one focus. If the path illustrated by the
graph shown is modeled by the equation
how close did
the comet get to the Sun? Assume units are in
millions of miles and round to the nearest
million.
Solution
䊳
We are essentially asked to find the distance
between a vertex and focus. Begin by writing
the equation in standard form:
given
divide by 846,400
This is a horizontal hyperbola with and
Use the foci formula to find c
2
and c.
Since and the comet came within about million
miles of the Sun.
Now try Exercises 81 through 84
䊳
50 ⫺ 20 ⫽ 30
冟
c
冟
⬇ 50,a ⫽ 20
c ⬇ ⫺50 and c ⬇ 50
c
2
⫽ 2516
c
2
⫽ 400 ⫹ 2116
c
2
⫽ a
2
⫹ b
2
b ⫽ 46 1b
2
⫽ 21162.a ⫽ 20 1a
2
⫽ 4002
x
2
20
2
⫺
y
2
46
2
⫽ 1
x
2
400
⫺
y
2
2116
⫽ 1
2116x
2
⫺ 400y
2
⫽ 846,400
2116x
2
⫺ 400y
2
⫽ 846,400,
1.6
6.3
1⫺3, 4 ⫺ 2.32⫽ 1⫺3, 1.62
⫽ 1⫺3, 6.3
21⫺3, 4 ⫹ 2.32
1⫺3, 42
7
3
⫽ 2.3.
b
2
⫽ 7a ⫽ 3
b
2
a
8–33 Section 8.3 The Hyperbola 739
College Algebra G&M—
⫺9.4 9.4
⫺2.2
10.2
Figure 8.35
(0, 0)
y
x
write denominators in
squared form
C. You’ve just seen how
we can locate the foci of a
hyperbola and use the foci and
other features to write its
equation
cob19545_ch08_731-745.qxd 10/25/10 9:24 PM Page 739
